Содержание
- 3. Из условия видим, что множество значений, которые может принимать y, удовлетворяет неравенству: y Избавимся от иррациональности.
- 4. Множество значений у: y - гипербола, О(3, 7), полуоси: мнимая а = 2, действительная b =
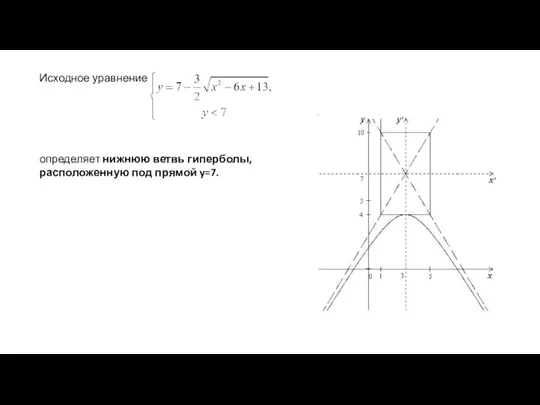
- 5. Исходное уравнение определяет нижнюю ветвь гиперболы, расположенную под прямой y=7.
- 6. Задача 2. Установите, какую линию определяет уравнение Нарисуйте ее график. Решение. или Вывод: исследуемое уравнение задает
- 7. Задача 3. Установите, какую линию определяет уравнение Нарисуйте ее график. Решение. Выделим полный квадрат: Тогда или
- 8. КРИВЫЕ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ РЕШЕНИЕ задач на построение
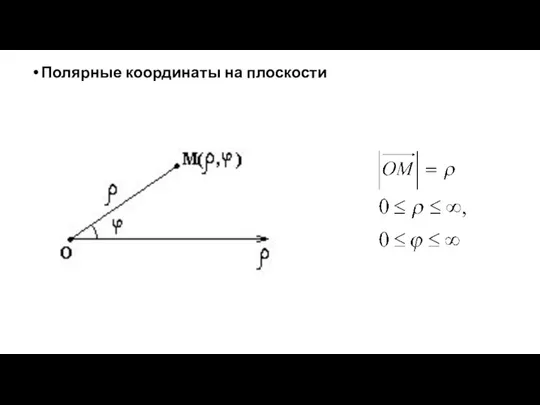
- 9. Полярные координаты на плоскости ,
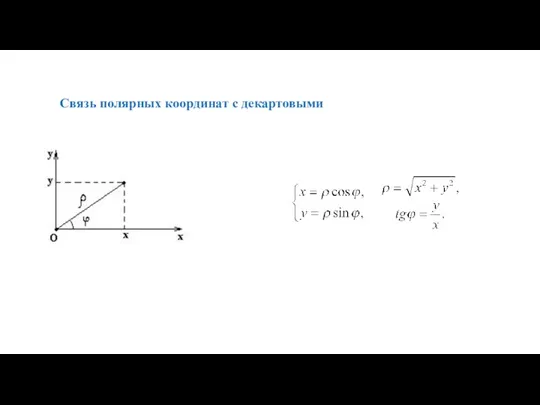
- 10. Связь полярных координат с декартовыми
- 11. как построить линию в полярной системе координат? – Сначала необходимо отметить полюс, изобразить полярную ось и
- 12. Задача 1. Решение. Найдем уравнение данной линии в прямоугольной системе координат. Воспользуемся уравнениями перехода из полярной
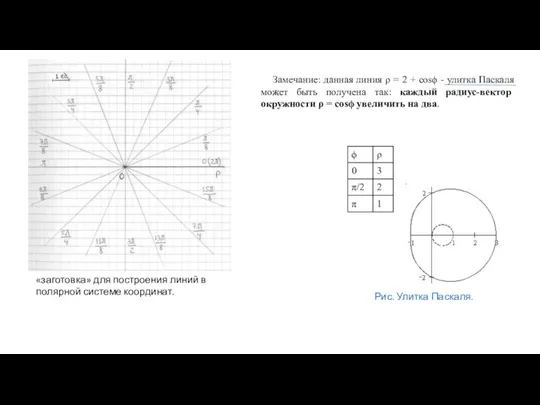
- 13. Задача 2. Постройте в полярной системе координат линию ρ = 2 + cosϕ. Решение. 1) Найдём
- 14. Замечание: данная линия ρ = 2 + cosϕ - улитка Паскаля может быть получена так: каждый
- 15. задача 3. Постройте в полярной системе координат линию . Решение. 1) составим таблицу пар точек, принадлежащих
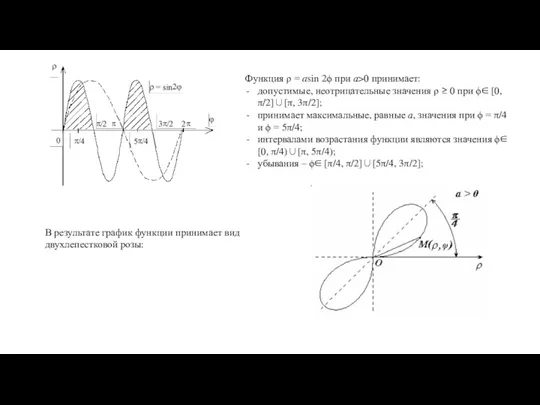
- 16. Функция ρ = asin 2ϕ при а>0 принимает: допустимые, неотрицательные значения ρ ≥ 0 при ϕ∈
- 17. Задача 4. Постройте в полярной системе координат линию Решение: Исходя из области определения переменной ρ, найдем
- 18. 16x2 + 16y2 = 25x2 + 90x + 81, 9x2 + 90x – 16y2 +81 =
- 20. Скачать презентацию












 Ашшур. Первая книга Царств 11:5,6. Часть 2. Лекция 2
Ашшур. Первая книга Царств 11:5,6. Часть 2. Лекция 2 Этиология заикания
Этиология заикания MP-60D. Особенности охранной системы
MP-60D. Особенности охранной системы Женский портрет
Женский портрет Презентация Социальный проект - Чистая вода - здоровье города.
Презентация Социальный проект - Чистая вода - здоровье города. Михаил Шолохов (1905-1984). Повесть Судьба человека
Михаил Шолохов (1905-1984). Повесть Судьба человека Формирование финансовых результатов компании с учетом налогообложения
Формирование финансовых результатов компании с учетом налогообложения Простейшие комбинаторные задачи
Простейшие комбинаторные задачи Гипертензивные расстройства. Преэклампсия. Эклампсия
Гипертензивные расстройства. Преэклампсия. Эклампсия Мастер-класс Законы золотого сечения в букете
Мастер-класс Законы золотого сечения в букете Презентация к ОД Лягушка
Презентация к ОД Лягушка Русь расправляет крылья. Урок ознакомления с окружающим миром.4 класс УМК Школа России
Русь расправляет крылья. Урок ознакомления с окружающим миром.4 класс УМК Школа России Измерительные устройства
Измерительные устройства Имя собственное. 1 класс
Имя собственное. 1 класс Текстовые редакторы
Текстовые редакторы Откуда приходит новый год
Откуда приходит новый год Рибні консерви і ікра риб
Рибні консерви і ікра риб Транссиб
Транссиб Изменения в законе РФ о занятости населения. Граждане предпенсионного возраста
Изменения в законе РФ о занятости населения. Граждане предпенсионного возраста Модульная технология обучения и её применение на уроках химии
Модульная технология обучения и её применение на уроках химии Мои 16 лет в педагогике
Мои 16 лет в педагогике ФГОС ДО для родителей
ФГОС ДО для родителей Charles Darwin
Charles Darwin Образовательный проект Как книга нас объединила
Образовательный проект Как книга нас объединила Презентация к внеклассному мероприятию Права детей Диск
Презентация к внеклассному мероприятию Права детей Диск Внутренний аудит как форма финансового контроля. Тема 1
Внутренний аудит как форма финансового контроля. Тема 1 Презентация Моя семья
Презентация Моя семья Промышленный переворот в Англии
Промышленный переворот в Англии