Содержание
- 2. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 3.1 Линии на плоскости и их уравнения 3.2 Прямая линия на плоскости 3.3
- 3. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 3.3 Кривые второго порядка 3.3.1 Эллипс 3.3.2 Гипербола 3.3.3 Парабола 3.3.4 Общее уравнение
- 4. 3.3.1 ЭЛЛИПС Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух
- 5. 3.3.1 ЭЛЛИПС – уравнение эллипса При помощи алгебраических преобразований и использования замены это уравнение можно упростить
- 6. 3.3.1 ЭЛЛИПС Свойства эллипса 1. Эллипс симметричен относительно координатных осей и относительно начала координат. – большая
- 7. 3.3.1 ЭЛЛИПС Эксцентриситет эллипса Отношение называется эксцентриситетом эллипса, оно характеризует степень сжатия эллипса. Чем больше эксцентриситет,
- 8. 3.3.1 ЭЛЛИПС Если ввести декартову систему координат так, чтобы фокусы лежали на оси Оу на одинаковом
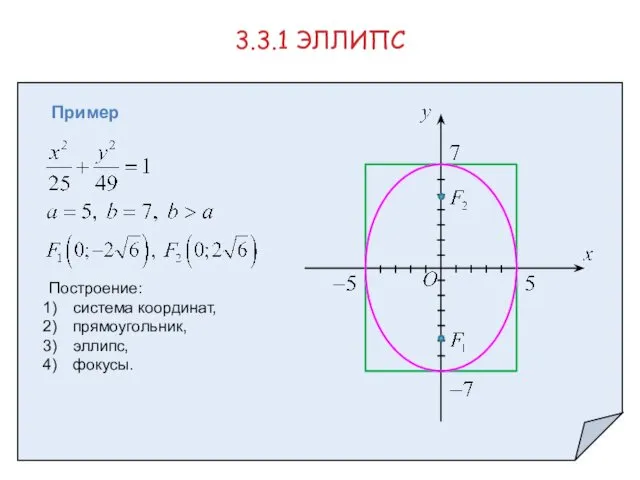
- 9. Пример Построить эллипс в декартовой системе координат и указать координаты его фокусов 3.3.1 ЭЛЛИПС - фокусы
- 10. Пример 3.3.1 ЭЛЛИПС Построение: система координат, прямоугольник, эллипс, фокусы.
- 11. 3.3.2 ГИПЕРБОЛА Гиперболой называется множество всех точек плоскости, разность расстояний от каждой из которых до двух
- 12. 3.3.2 ГИПЕРБОЛА – уравнение гиперболы При помощи алгебраических преобразований и использования замены это уравнение можно упростить
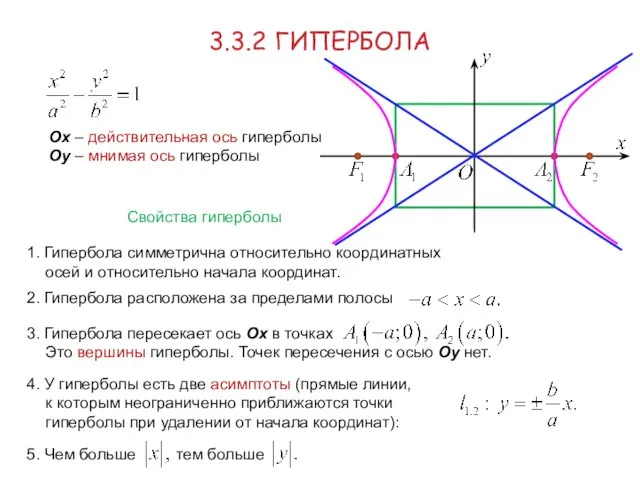
- 13. 3.3.2 ГИПЕРБОЛА Свойства гиперболы 1. Гипербола симметрична относительно координатных осей и относительно начала координат. Ох –
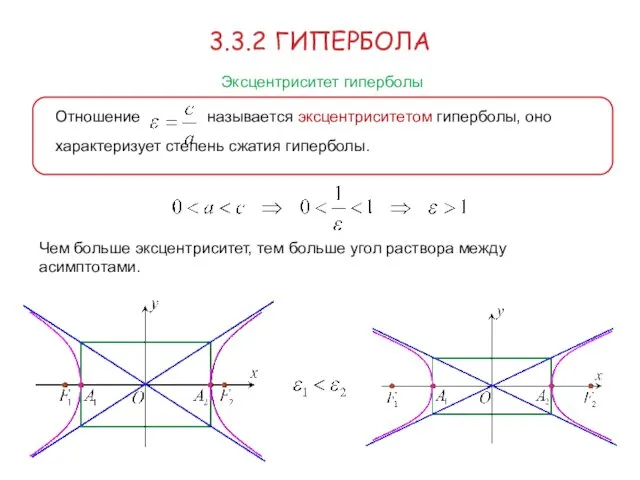
- 14. 3.3.2 ГИПЕРБОЛА Эксцентриситет гиперболы Отношение называется эксцентриситетом гиперболы, оно характеризует степень сжатия гиперболы. Чем больше эксцентриситет,
- 15. 3.3.2 ГИПЕРБОЛА Если ввести декартову систему координат так, чтобы фокусы лежали на оси Оу на одинаковом
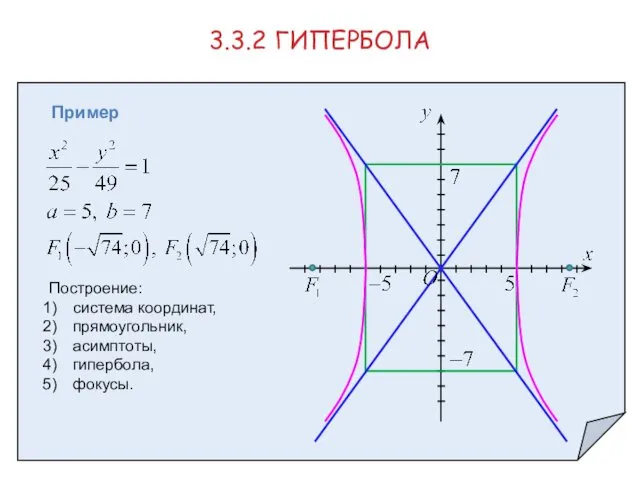
- 16. Пример Построить гиперболу в декартовой системе координат и указать координаты её фокусов 3.3.2 ГИПЕРБОЛА - фокусы
- 17. Пример 3.3.2 ГИПЕРБОЛА Построение: система координат, прямоугольник, асимптоты, гипербола, фокусы.
- 18. 3.3.3 ПАРАБОЛА Параболой называется множество всех точек плоскости, равноудалённых от фиксированной точки (фокуса) и прямой (директрисы).
- 19. 3.3.3 ПАРАБОЛА – уравнение параболы Возведём обе части в квадрат и приведём подобные каноническое уравнение параболы
- 20. 3.3.3 ПАРАБОЛА Свойства параболы 1. Парабола симметрична относительно оси Ох. 2. Парабола проходит через начало координат
- 21. 3.3.3 ПАРАБОЛА Замечание Если расположить систему координат по-другому, то получим ещё три канонических уравнения параболы.
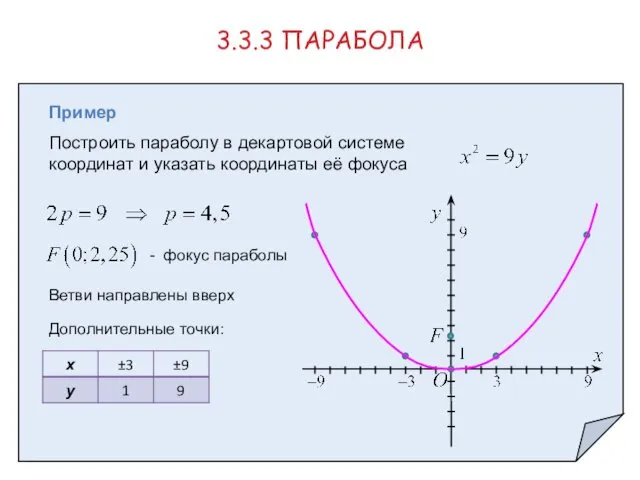
- 22. Пример Построить параболу в декартовой системе координат и указать координаты её фокуса 3.3.3 ПАРАБОЛА - фокус
- 23. 3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ Это общее уравнение кривой
- 24. Пример Привести к каноническому виду уравнение Указать тип кривой и сделать чертёж в системе координат. Решение:
- 25. Пример Решение (продолжение): 4) Свернём полные квадраты, используя формулы сокращённого умножения 3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
- 26. Пример Решение (продолжение): 8) Сделаем замену 3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА И ПРИВЕДЕНИЕ ЕГО К
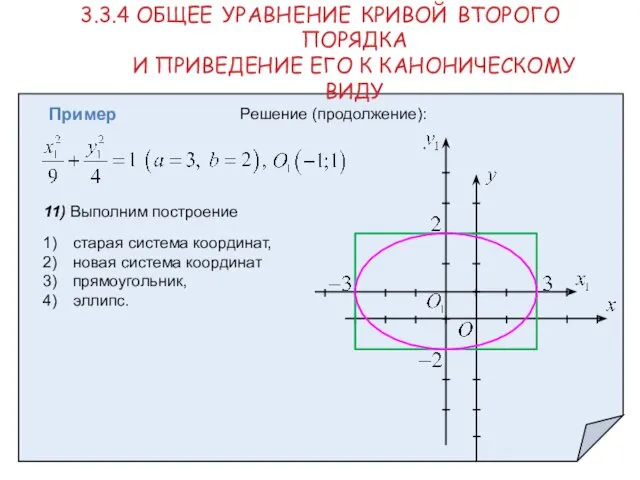
- 27. Пример Решение (продолжение): 11) Выполним построение 3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА И ПРИВЕДЕНИЕ ЕГО К
- 30. Скачать презентацию




















 Психология пищевого поведения подростков и взрослых
Психология пищевого поведения подростков и взрослых Колоректальный рак
Колоректальный рак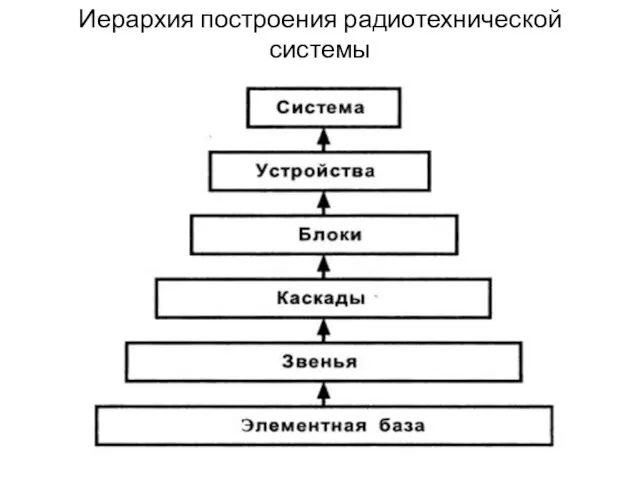 Иерархия построения радиотехнической системы
Иерархия построения радиотехнической системы ПРЕЗЕНТАЦИЯ ДЛЯ ВОСПИТАТЕЛЕЙ ТРЕБОВАНИЯ К ОРГАНИЗАЦИИ КНИЖНОГО УГОЛКА
ПРЕЗЕНТАЦИЯ ДЛЯ ВОСПИТАТЕЛЕЙ ТРЕБОВАНИЯ К ОРГАНИЗАЦИИ КНИЖНОГО УГОЛКА Государство Украина
Государство Украина Краеведение - наука о местности, в которой мы живём. Предмет биологического краеведения.
Краеведение - наука о местности, в которой мы живём. Предмет биологического краеведения. Формы организации производства
Формы организации производства С днем рождения, Ксюша
С днем рождения, Ксюша Продолжение Электронное портфолио 23 февраля
Продолжение Электронное портфолио 23 февраля 17.04. Літ. чит. М. Трублаїні Шоколад
17.04. Літ. чит. М. Трублаїні Шоколад Сильвестр Ольшевский, архиепископ Омский
Сильвестр Ольшевский, архиепископ Омский Первичная обр.рыбы
Первичная обр.рыбы Виды и оформление организационно-распорядительной документации
Виды и оформление организационно-распорядительной документации Кубань в каменном веке
Кубань в каменном веке Детёныши животных
Детёныши животных Изображение фигуры человека
Изображение фигуры человека Ф. И. Тютчев. 1803 – 1873 гг. Страницы биографии и творчества
Ф. И. Тютчев. 1803 – 1873 гг. Страницы биографии и творчества Культура речи, как основа эффективного общения
Культура речи, как основа эффективного общения Пищевые связи в экосистеме. Трофические уровни. Типы пищевых цепей
Пищевые связи в экосистеме. Трофические уровни. Типы пищевых цепей Генеральный план. Благоустройство территории
Генеральный план. Благоустройство территории Великобритания на рубеже XIX-XX веков
Великобритания на рубеже XIX-XX веков Легендарный разведчик Николай Иванович Кузнецов
Легендарный разведчик Николай Иванович Кузнецов Кавказские Минеральные Воды
Кавказские Минеральные Воды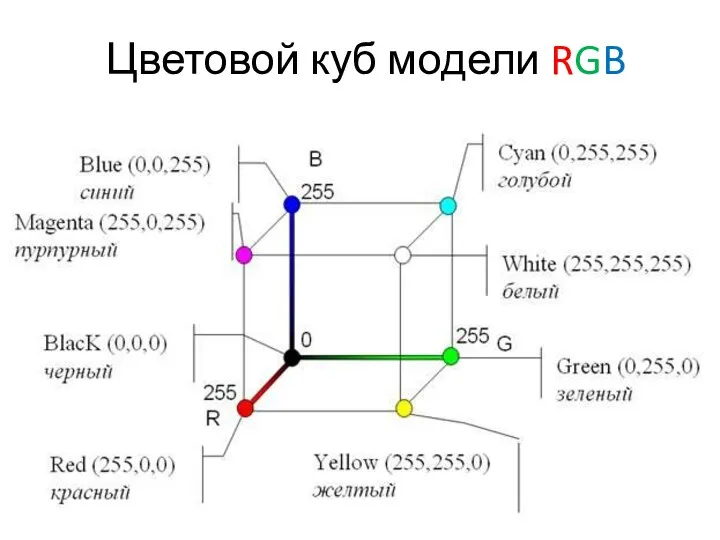 карточка RGB Диск
карточка RGB Диск Методы медицинской генетики человека
Методы медицинской генетики человека Повышение надежности систем электроснабжения
Повышение надежности систем электроснабжения Древняя Индия
Древняя Индия Явление царя. Подвиг искупления
Явление царя. Подвиг искупления