Аналитические функции распределения, используемые в гидрологии презентация

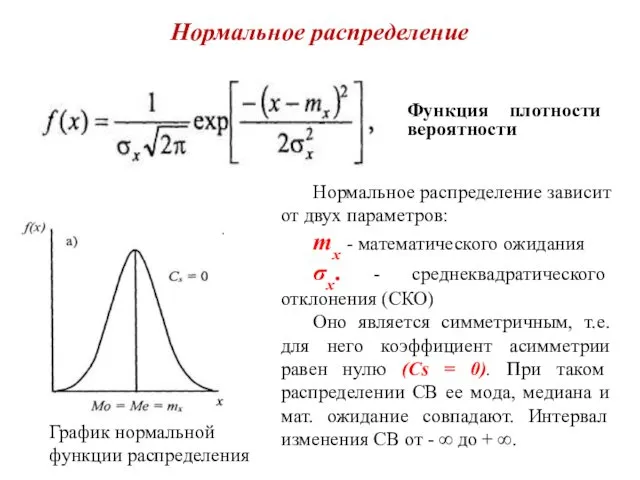
Нормальное распределение
Функция плотности вероятности
График нормальной функции распределения
Нормальное распределение зависит от двух параметров:
mx - математического ожидания
σx. - среднеквадратического отклонения (СКО)
Оно является симметричным, т.е. для него коэффициент асимметрии равен нулю (Cs = 0). При таком распределении СВ ее мода, медиана и мат. ожидание совпадают. Интервал изменения СВ от - ∞ до + ∞.

Интегральная
функция нормального распределения
Ординаты функции выражаются в виде таблицы. Рассматривается нормированная случайная величина – СВt , чтобы не публиковать различные значения для различных значений mx и σx.
где z – переменная интегрирования

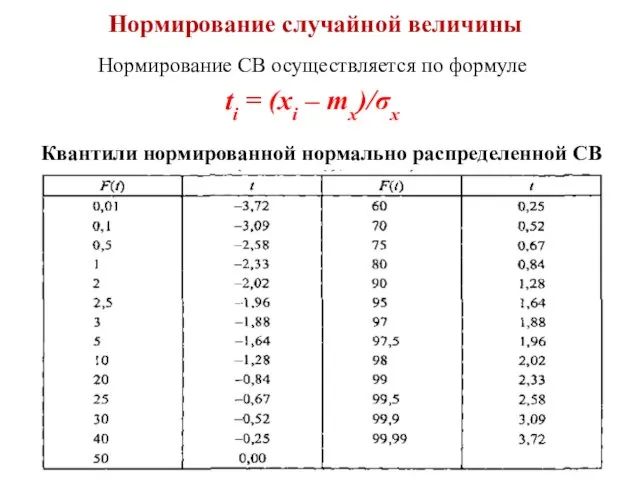
Нормирование случайной величины
Нормирование СВ осуществляется по формуле
ti = (xi – mx)/σx
Квантили нормированной нормально распределенной СВ

Переход
от нормированных значений СВ к исходным
Для расчета модульных коэффициентов используется формула kp = tpCv + 1
Перевод от нормированных значений СВ к исходным осуществляется по формуле xp = tp σx + mx
Нормальный закона
и гидрологические процессы
Расходы воды всегда положительны, а область значений СВ при нормальном распределении изменяется от - ∞ до + ∞
Для нормального распределения Cs = 0, а для многих гидрологических характеристик Cs >0.

Закон равномерной плотности
СВ Х подчиняется закону равномерной плотности, когда ни одному значению СВ Х не отдается предпочтение
Дифференциальная функция распределения закона равномерной плотности
Закон равномерной плотности определяется двумя параметрами: началом – а и концом – b интервала изменения СВ Х.
Плотность вероятности равна:

Интегральная функция
распределения закона равномерной плотности
Характерные особенности закона равномерной плотности распределения СВ:
- Медиана равна МО.
- Закон равномерной плотности не имеет Моды
Этот закон используется в гидрологии при моделировании искусственных гидрологических рядов.

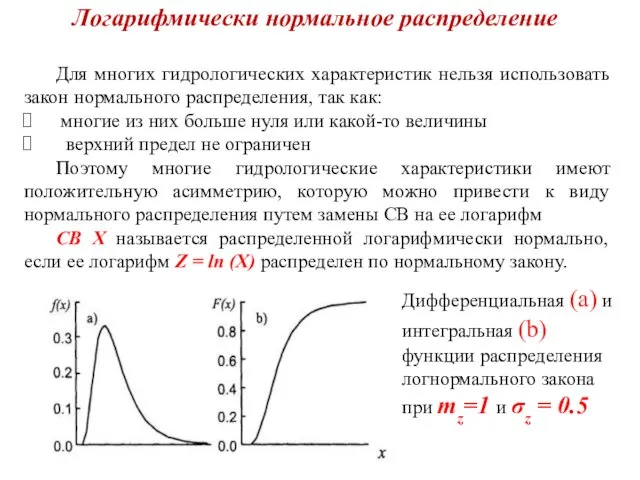
Логарифмически нормальное распределение
Для многих гидрологических характеристик нельзя использовать закон нормального распределения, так как:
многие из них больше нуля или какой-то величины
верхний предел не ограничен
Поэтому многие гидрологические характеристики имеют положительную асимметрию, которую можно привести к виду нормального распределения путем замены СВ на ее логарифм
СВ Х называется распределенной логарифмически нормально, если ее логарифм Z = ln (X) распределен по нормальному закону.
Дифференциальная (а) и интегральная (b) функции распределения логнормального закона при mz=1 и σz = 0.5

Интегральная и дифференциальная
функции логнормального распределении СВ
Интегральная функция логнормального распределения
Дифференциальная функция логнормального распределения
где u = (z- mz)/σz z = ln(x) s – переменная интегрирования

Характеристики логнормального распределения
Распределение определяется двумя параметрами: mz и σz
Величина mz – это МО, а σz – это СКО
Дисперсия, СКО и МО связаны соотношениями

Характеристики логнормального распределения (2)
Наибольшее соответствие эмпирических данных с логнормальным распределением случается при Cs/Cv = 3 – 3,5
Мода и медиана для СВ Х, имеющего логнормальное распределение, определяются равенствами:
Ординаты кривой обеспеченности логнормального распределения определяются по таблице стандартного нормального закона распределения, с учетом того, что Z = ln (X)
Cs = 3•Cv + Cv3
где Cv = σ/mx
Коэффициент асимметрии логнормального распределения определяется по формуле

Последовательность
расчетов среднегодовых расходов воды n% обеспеченности – P(n%) при логнормальном распределении
Так как на практике мы не знаем истинное распределение СВ Х, то допускается два варианта расчета:
оценка mz и σz производится по ряду значений СВ Z
по ряду значений СВ Х производится оценка mx и σx, а затем по формулам
определяется mz и σz

Последовательность расчетов (1 вариант)
Проводим преобразование исходного ряда наблюдений по формуле zi = lnQi
По ряду значений СВ Z приближенно определяем mz и σz (методика расчета будет изложена в последующих лекциях)
Вычисляем вероятность непревышения F(n%)=100 – P(n%)
По таблице квантилей для нормированной нормально распределенной СВt определяем F(n%) квантиль
по формуле xp=tpσp + mx определяем zp(n%) = tp(n%)σz + mz
Так как zp(n%) = ln Qp(n%), то Qp(n%) = exp (zp(n%)

Последовательность расчетов (2 вариант)
По исходному ряду определяем приближенно mx и σx
Вычисляем mz и σz по формулам
Дальнейший расчет проводится аналогично первому варианту

Трехпараметрическое логнормальное распределение
В этом распределении вместо преобразования Z = ln(X) используется преобразование Z = ln (X-a), где a – дополнительный третий параметр
Параметр a связан с коэффициентом асимметрии соотношением
где k0 – минимальный модульный коэффициент, k0 = a/mx. При k0 = 0, это выражение превращается в выражение
Этот тип распределения рекомендуется использовать при

Закон распределения
крайних членов выборки (распределение Гумбеля)
Закон разработан для расчетов СВ, связанных с экстремальными случаями (максимальные суточные расходы ….)
Функция обеспеченностей закона Гумбеля выглядит так
где у – безразмерная величина, связанная с х выражением
y = α(x – q)
где q - мода СВ Х, которая определяется в зависимости от среднего значения и СКО исходного ряда по формуле
а величину α можно выразить как

Распределение Гумбеля (продолжение)
На практике вместо уравнения
используется уравнение, полученное при его решении относительно х
Значение ур можно получить из выражения
после двух- кратного логарифмирования
где р - расчетная обеспеченность в процентах. Для основных опорных обеспеченностей значения ур приводятся в таблице

Распределение Гумбеля (продолжение)
Теңдеуі:
және
q және α параметрлерін
-пен байланыстырады σx при n →∞
Для конечных выборок Гумбель предложил формулы
и
Параметры
и σy определяются в зависимости от длины
анализируемого ряда

Распределение Гумбеля (жалғасы)
Формуласын ескерсек,
выражение плотности вероятности распределения Гумбеля имеет вид
Из выражения видно, что для распределения Гумбуля область возможных значений СВ Х находится в интервале (-∞, +∞). Распределение двухпараметрическру т.е. определяется параметрами
и σx.
распределение Гумбеля используется, в основном, при расчете дождевых паводков.