Содержание
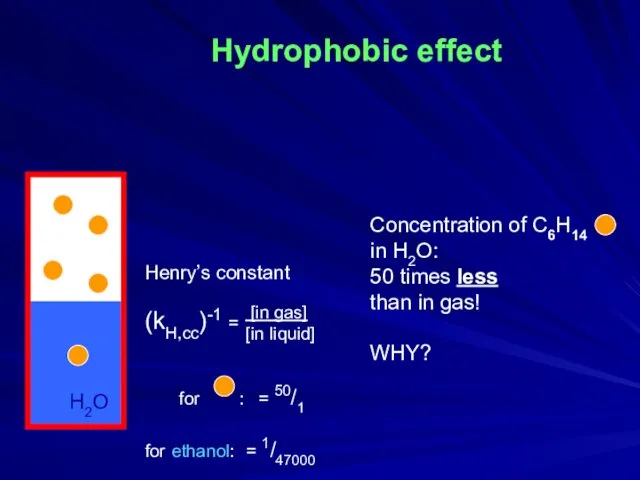
- 2. Hydrophobic effect Concentration of C6H14 in H2O: 50 times less than in gas! WHY? H2O Henry’s
- 3. ENTROPY: SE = kB • ln[ME]; ME=number_of_states(E) Why kB? What is kB? Because entropy SE comes
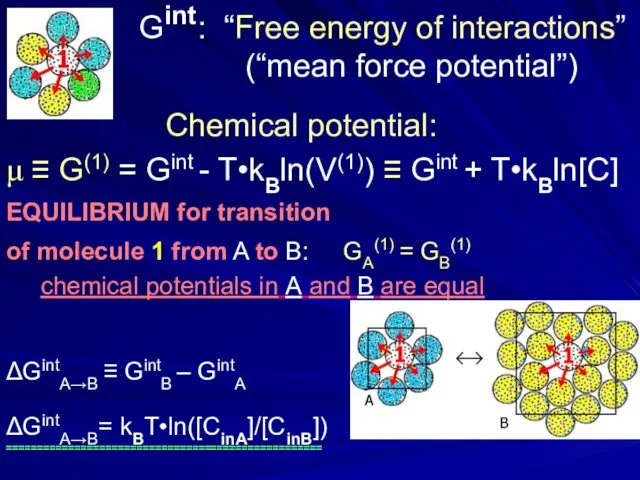
- 4. Gint : “Free energy of interactions” (“mean force potential”) Chemical potential: μ ≡ G(1) = Gint
- 5. Experiment: ΔG intA→B= kBT•ln([C1 in A]/[C1 in B]) ΔSintA→B = -d(ΔGintA→B)/dT ΔHintA→B = ΔGintA→B +TΔSintA→B C6H12
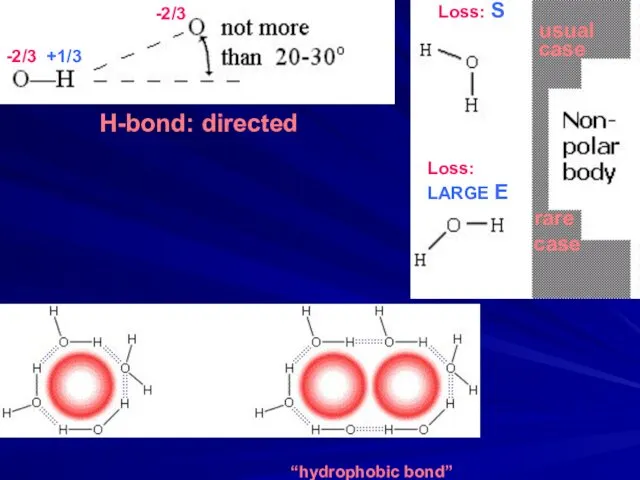
- 6. -2/3 +1/3 Loss: S usual case -2/3 Loss: LARGE E rare case H-bond: directed “hydrophobic bond”
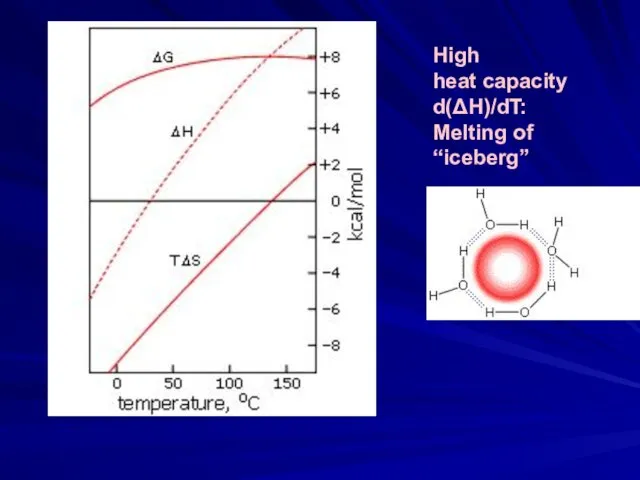
- 7. High heat capacity d(ΔH)/dT: Melting of “iceberg”
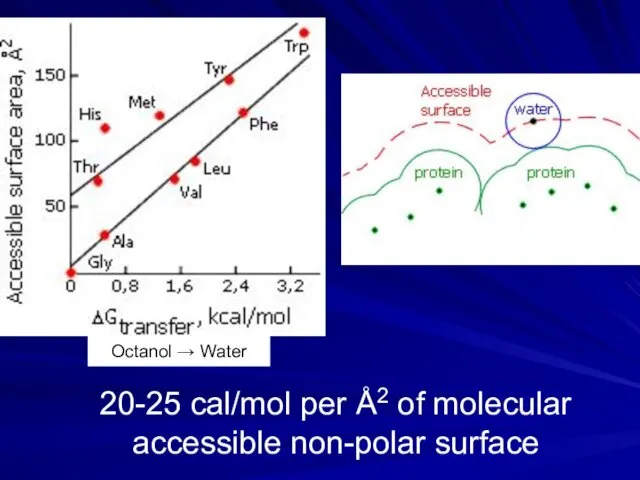
- 8. 20-25 cal/mol per Å2 of molecular accessible non-polar surface Octanol → Water
- 9. Семён Ефимович Бреслер (1911 – 1983) Давид Львович Талмуд (1900 - 1973) Cyrus Homi Chothia, 1942
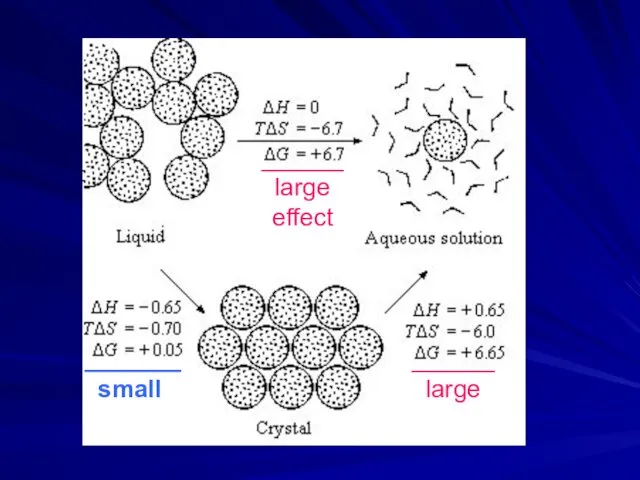
- 10. ______ large effect _______ small ______ large
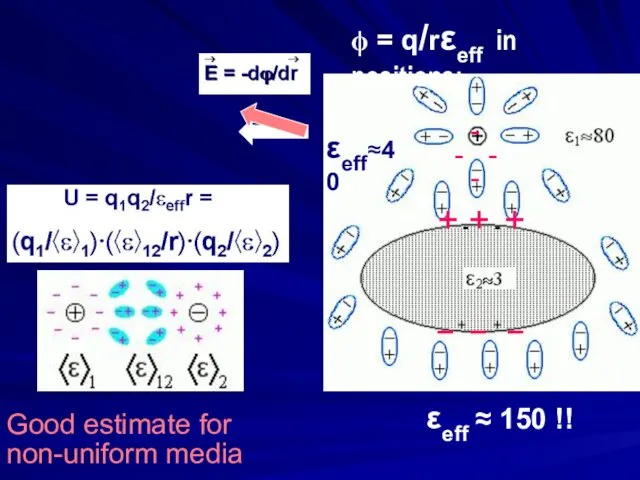
- 11. Electrostatics in uniform media: potential ϕ1 = q1/εr Interaction of two charges: U = ϕ1q2 =
- 12. (1736-1806)
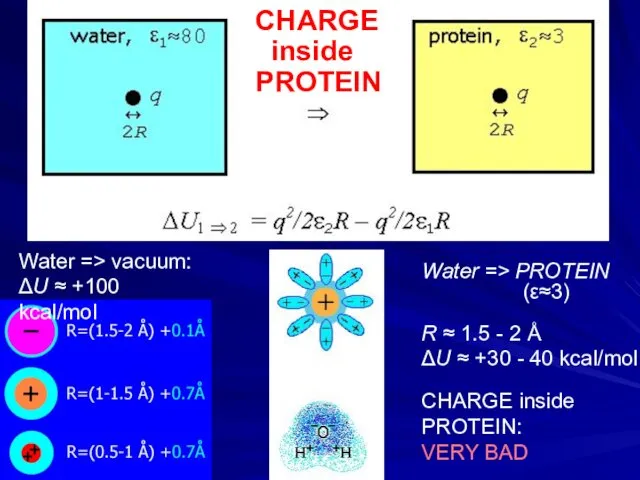
- 13. Water => PROTEIN (ε≈3) R ≈ 1.5 - 2 Å ΔU ≈ +30 - 40 kcal/mol
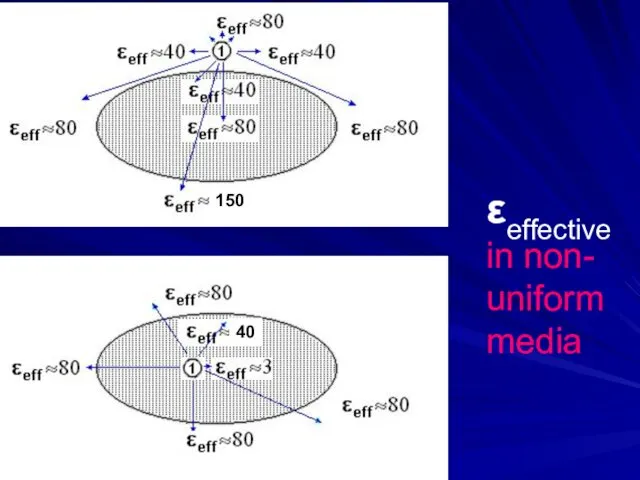
- 14. Non-uniform media: εeff = ?
- 15. Non-uniform media: εeff = ?
- 16. Non-uniform media: εeff = ? intermediate dipole
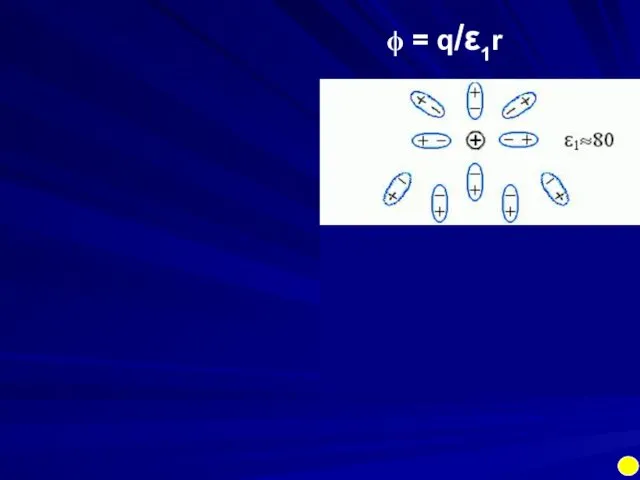
- 17. ϕ = q/ε1r
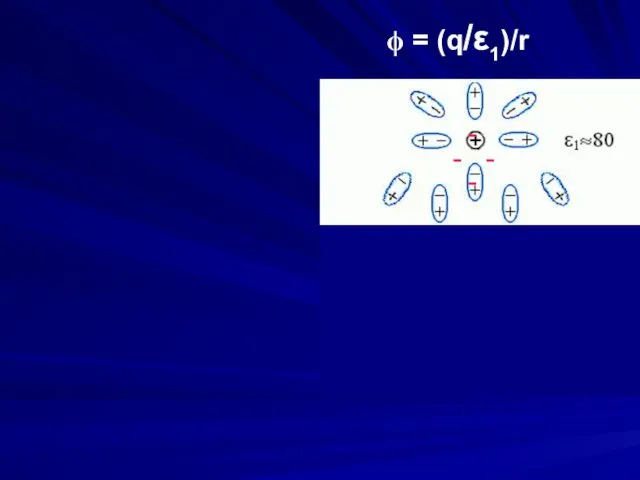
- 18. - - - - ϕ = (q/ε1)/r
- 19. Good estimate for non-uniform media + -+ - + – + – + – εeff ≈
- 20. εeffective in non- uniform media 150 40
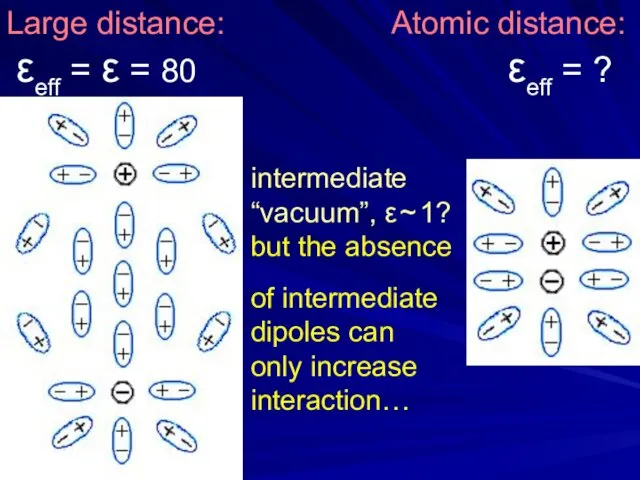
- 21. Large distance: Atomic distance: εeff = ε = 80 εeff = ? intermediate “vacuum”, ε ~
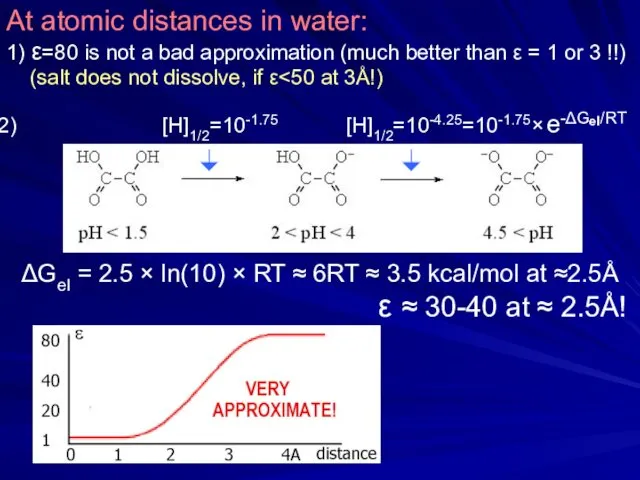
- 22. At atomic distances in water: 1) ε=80 is not a bad approximation (much better than ε
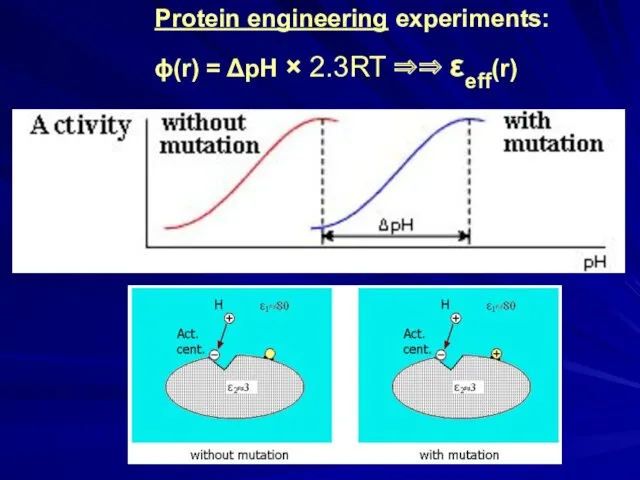
- 23. Protein engineering experiments: ϕ(r) = ΔpH × 2.3RT ⇒⇒ εeff(r)
- 24. Sir Alan Roy Fersht, 1943 Protein engineering
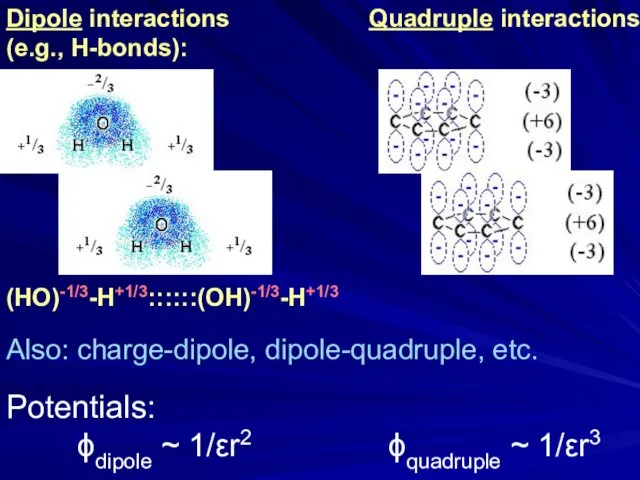
- 25. Dipole interactions (e.g., H-bonds): (HO)-1/3-H+1/3::::::(OH)-1/3-H+1/3 Quadruple interactions Also: charge-dipole, dipole-quadruple, etc. Potentials: ϕdipole ~ 1/εr2 ϕquadruple
- 26. Electrostatic interactions also occur between charge (q) and non-charged body, if its ε2 differs from the
- 27. Debye-Hückel screening of electrostatic by ions: U = [q1q2/εr]•exp(-r/D) ; in water: D = 3Å•I-1/2; Ionic
- 28. Electrostatics is T- dependent; U = (1/ε)•(q1q2/r) is free energy (U = H-TS); TS = T•(-dU/dT)
- 29. S-S bonds (Cys-Cys) exchange: entropic force S-S bond is not stable within a cell
- 31. Скачать презентацию
![ENTROPY: SE = kB • ln[ME]; ME=number_of_states(E) Why kB? What](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/28776/slide-2.jpg)
![Experiment: ΔG intA→B= kBT•ln([C1 in A]/[C1 in B]) ΔSintA→B =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/28776/slide-4.jpg)








![Debye-Hückel screening of electrostatic by ions: U = [q1q2/εr]•exp(-r/D) ;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/28776/slide-26.jpg)


 kak_stat_uspeshnym_chelovekom
kak_stat_uspeshnym_chelovekom Логика. Умозаключение
Логика. Умозаключение Война за независимость и образование США
Война за независимость и образование США Виды сов
Виды сов Презентация по географии в 10 классе по теме Научно-техническая революция и Мировое хозяйство
Презентация по географии в 10 классе по теме Научно-техническая революция и Мировое хозяйство Нормативная база по противодействию курению
Нормативная база по противодействию курению Способы обнаружения и устранения неисправностей и последовательность проверки работоспособности радиоприемника
Способы обнаружения и устранения неисправностей и последовательность проверки работоспособности радиоприемника 1_Введение
1_Введение Профессии будущего
Профессии будущего Социальная структура общества
Социальная структура общества Present continuous
Present continuous Поверхности нагрева паровых котлов
Поверхности нагрева паровых котлов Фотосинтез процесі
Фотосинтез процесі Фразеология. Фразеологические сращения. Фразеологические единства
Фразеология. Фразеологические сращения. Фразеологические единства ОМРК Добро и зло.
ОМРК Добро и зло. Всемирная сеть СТО. Компания Bosch
Всемирная сеть СТО. Компания Bosch Сүйек буын туберкулезі
Сүйек буын туберкулезі Методы арт-терапии в образовательном процессе ДОУ
Методы арт-терапии в образовательном процессе ДОУ Лабораторная диагностика вирусных инфекций
Лабораторная диагностика вирусных инфекций Ветер
Ветер Электроэнергетика мира
Электроэнергетика мира Дидактические игры по ФЭМП по Тихеевой
Дидактические игры по ФЭМП по Тихеевой Компоновка поперечной рамы
Компоновка поперечной рамы Презентация Несуществующие дорожные знаки Диск
Презентация Несуществующие дорожные знаки Диск Тематика задач на ЕГЭ по математике
Тематика задач на ЕГЭ по математике Интеллектуальная игра Брей-ринг
Интеллектуальная игра Брей-ринг Артикуляционная гимнастика
Артикуляционная гимнастика Новые подходы к изучению истории Великой Отечественной войны и их отражение в школьных учебниках
Новые подходы к изучению истории Великой Отечественной войны и их отражение в школьных учебниках