Содержание
- 2. Часть 3 Осевая симметрия
- 3. Симметрия «Симметрия» - слово греческого происхождения. Оно, как и слово «гармония», означает «соразмерность», «наличие определенного порядка,
- 4. Точка, симметричная относительно прямой Возьмем лист бумаги. Проведем на нем прямую и перегнем лист по этой
- 5. Построение точки, симметричной относительно прямой Пусть даны прямая l и точка M. Построим точку, симметричную точке
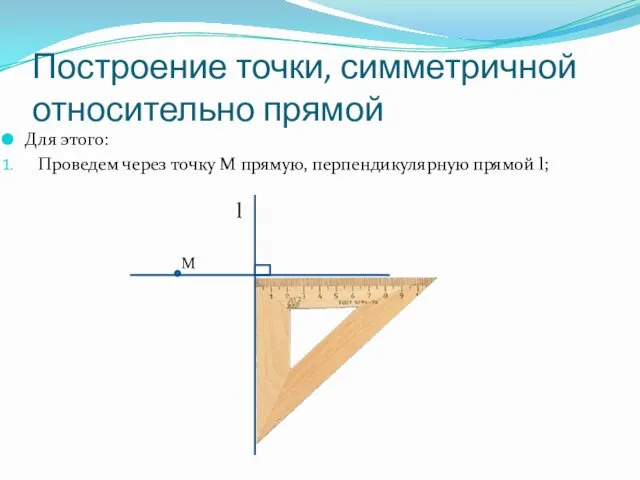
- 6. Построение точки, симметричной относительно прямой Для этого: Проведем через точку M прямую, перпендикулярную прямой l; l
- 7. Построение точки, симметричной относительно прямой Отметим на ней точку K, расположенную на таком же расстоянии от
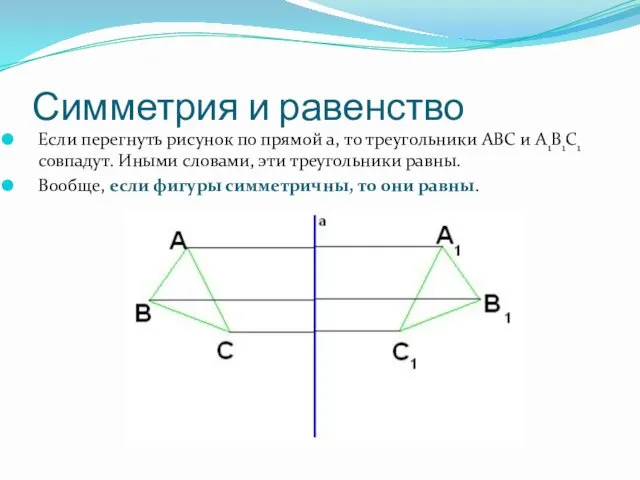
- 8. Симметрия и равенство Если перегнуть рисунок по прямой a, то треугольники ABC и A1B1C1 совпадут. Иными
- 9. Упражнения Ищем симметрию. 1 2 3 Подсказка. Выполняя задание, вы можете проверить себя, воспользовавшись зеркалом.
- 10. Упражнения Художник перерисовал картинку симметрично, относительно вертикальной прямой, но сделал 5 ошибок. Найдите эти ошибки.
- 11. Упражнения Построение фигур, симметричных, относительно прямой. Перенесите рисунок в тетрадь и постройте точки, симметричные точкам A,
- 12. Симметричная фигура Мы рассмотрели случай, когда две фигуры симметричны относительно некоторой прямой. Но прямая может пройти
- 13. Упражнения. Симметрия и координатная плоскость На координатной плоскости постройте треугольник ABC по координатам его вершин: A(2;2),
- 14. Упражнения. Симметрия и координатная плоскость Отметьте на координатной плоскости все точки, у которых ордината и абсцисса
- 16. Скачать презентацию











 Нормативно-правовая база
Нормативно-правовая база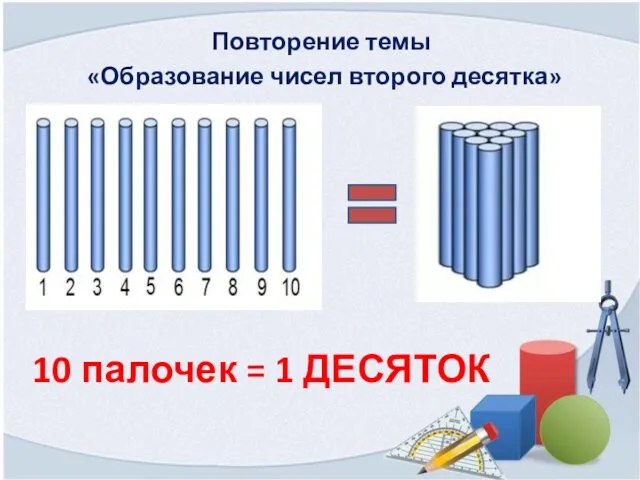 Образование чисел второго десятка. 1 класс
Образование чисел второго десятка. 1 класс Обучающее сочинение по картине А.К.Саврасова Грачи прилетели
Обучающее сочинение по картине А.К.Саврасова Грачи прилетели Первая оценка и как к ней относится
Первая оценка и как к ней относится Как и где зимуют птицы (1 класс)
Как и где зимуют птицы (1 класс) Макроэкономика. Макроэкономическая нестабильность: циклическое развитие экономики, инфляция, безработица. Тема 4
Макроэкономика. Макроэкономическая нестабильность: циклическое развитие экономики, инфляция, безработица. Тема 4 Табличные информационные модели. Моделирование и формализация
Табличные информационные модели. Моделирование и формализация Өсімдіктердің вегетация кезеңінде синтетикалық пиретроидтарға. Жататын инсектицидтерді қолдану
Өсімдіктердің вегетация кезеңінде синтетикалық пиретроидтарға. Жататын инсектицидтерді қолдану познавательные ууд
познавательные ууд Организация учебно- воспитательного процесса в условиях ФГОС
Организация учебно- воспитательного процесса в условиях ФГОС Презентация занятия Осеннее дерево
Презентация занятия Осеннее дерево Профилактика вредных привычек
Профилактика вредных привычек Расстройства аффективного спектра
Расстройства аффективного спектра Математика и наше здоровье
Математика и наше здоровье 9 класс.Электив. Уравнения с модулем -4.
9 класс.Электив. Уравнения с модулем -4. Фенол. 10 класс
Фенол. 10 класс Системы счисления. Древние системы счисления
Системы счисления. Древние системы счисления Презентация Цветочные фантазии из фетра. Мастер-класс
Презентация Цветочные фантазии из фетра. Мастер-класс Высотная поясность.
Высотная поясность. Латинская Америка в XIX – начале XX в.: время перемен
Латинская Америка в XIX – начале XX в.: время перемен Республика Молдова
Республика Молдова Географические координаты
Географические координаты Порядок проведения мероприятий по надзору (контролю) сотрудниками государственного пожарного надзора
Порядок проведения мероприятий по надзору (контролю) сотрудниками государственного пожарного надзора Writing an essay (C2)
Writing an essay (C2) Искусственные нейронные сети. Лекция 15-16
Искусственные нейронные сети. Лекция 15-16 Классный час Поговорим о здоровье Классный час Поговорим о здоровье. Здоровье — это здоровый образ жизни
Классный час Поговорим о здоровье Классный час Поговорим о здоровье. Здоровье — это здоровый образ жизни Заполнение бланков участников итогового сочинения (изложения)
Заполнение бланков участников итогового сочинения (изложения) Дробь как одна или несколько равных долей
Дробь как одна или несколько равных долей