Слайд 2

где коэффициенты А,В,С одновременно не обращаются в нуль. При А
= В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка.
К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
Слайд 3

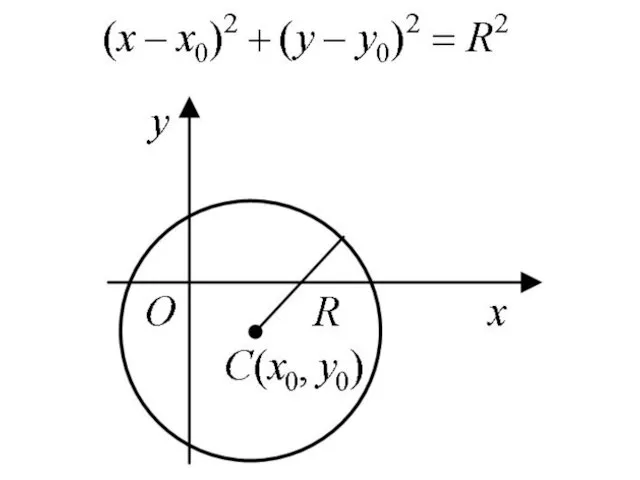
Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра).
Если центр
окружности поместить в начало координат, то каноническое уравнение окружности радиусом R имеет вид
Слайд 4

Если центр окружности находится в точке C(x0, y0), то ее уравнение
записывается в виде
Слайд 5
Слайд 6

Пусть на плоскости заданы две точки F1 и F2, расстояние между
которыми равно 2с, и задано число a > c.
Слайд 7

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух
данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 8
Слайд 9

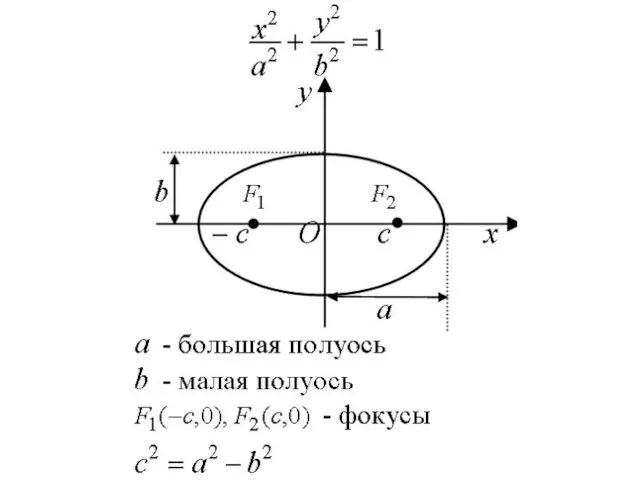
Если систему координат выбрать так, как указано на рис., то каноническое
уравнение эллипса запишется в виде
где а – большая, b – малая полуоси эллипса (при a>b).
Слайд 10

Фокусы эллипса расположены в точках F1(-c; 0) и F2(c; 0).
Окружность
есть частный случай эллипса при a = b.
Слайд 11

Пусть на плоскости заданы две точки F1 и F2, расстояние между
которыми равно 2с, и задано число a < c.
Слайд 12

Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до
двух данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 13
Слайд 14

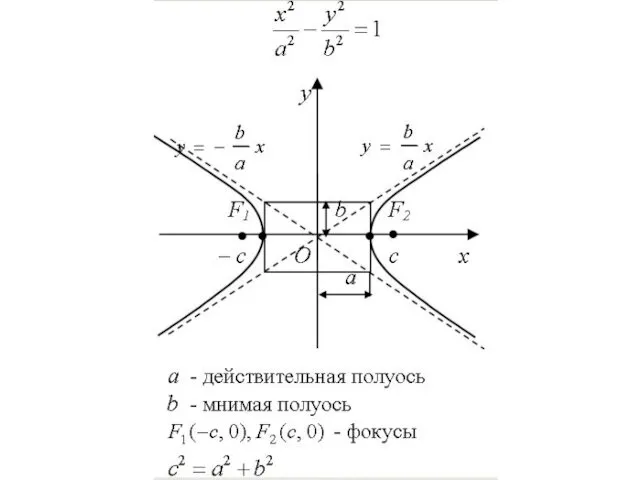
Если систему координат выбрать так, как указано на рис., то каноническое
уравнение гиперболы запишется в виде
где
а – действительная, b – мнимая полуоси гиперболы.
Слайд 15

Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей.
При этом ее ветви при удалении в бесконечность как угодно близко подходят к прямым которые называются асимптотами гиперболы.
Слайд 16

При построении гиперболы вначале строят основной прямоугольник со сторонами x =
± a, y = ± b. Затем через противоположные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы.
Слайд 17

Вершины гиперболы расположены в точках с координатами (– а,0) и (а,0),
а фокусы – в точках F1(-c; 0) и F2(c; 0).
Слайд 18

Уравнение
(или ) также задаёт гиперболу, сопряженную с гиперболой
Действительная и мнимая полуоси этой гиперболы соответственно равны b и а.
Слайд 19

Пусть на плоскости задана точка F и прямая D, расстояние между
которыми равно р.
Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).
Слайд 20
Слайд 21

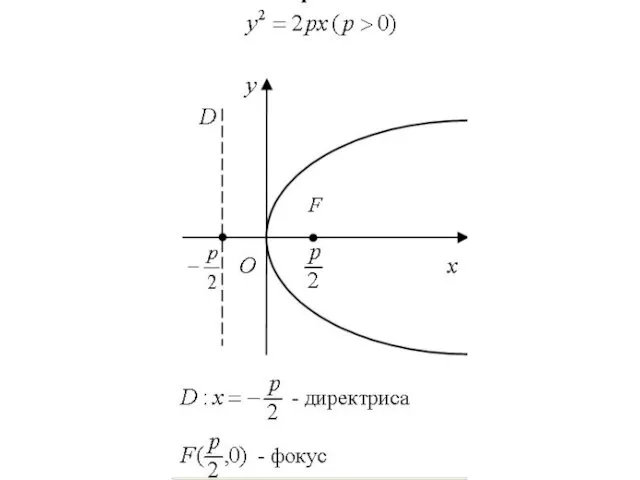
Если систему координат выбрать так, как указано на рис., то каноническое
уравнение параболы запишется в виде
Слайд 22

Эта парабола симметрична относительно оси Ох. Директрисой является прямая
точка
– фокус параболы, р – параметр параболы.
Слайд 23

Если p < 0, то парабола направлена в противоположную сторону.
Уравнение
задаёт параболу, симметричную относительно оси Оу.
Слайд 24

Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение
кривой приводят к каноническому виду и переходят к новой системе координат.
Слайд 25

Пример. Определить тип линии и схематически построить её:
Слайд 26

Решение. Приведем заданное уравнение к каноническому виду. Для этого в исходном
уравнении выделим полные квадраты по переменным х и у. Перепишем исходное уравнение в виде:
Слайд 27
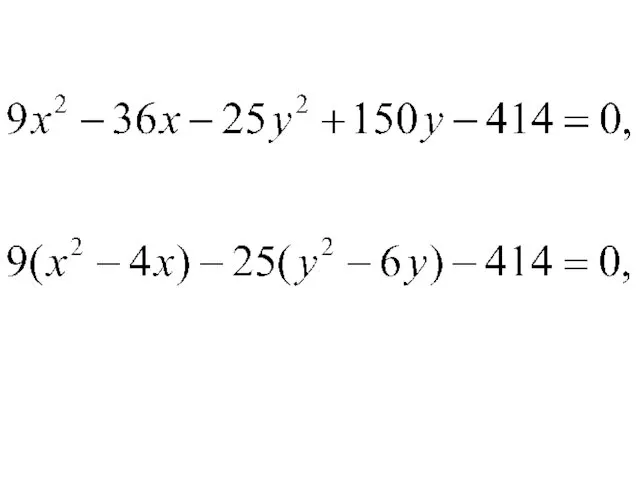
Слайд 28
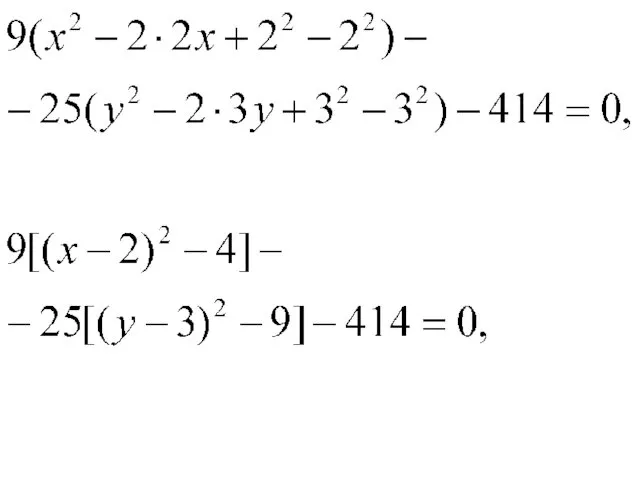
Слайд 29
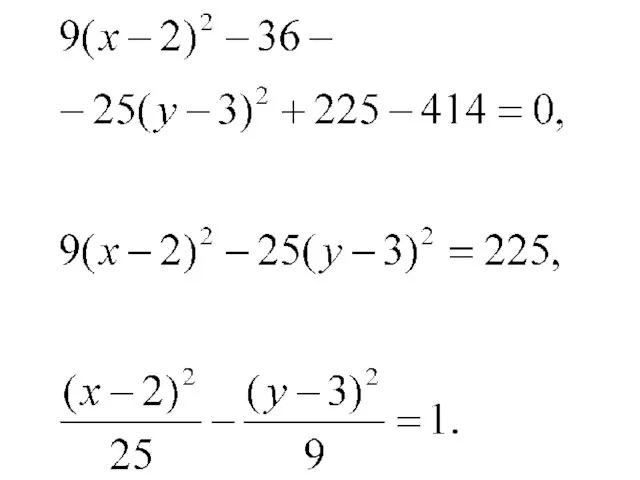
Слайд 30

Совершим параллельный перенос координатных осей по формулам:
(2, 3) –
координаты центра O1 системы координат X и Y. В этой системе координат уравнение принимает вид:
Слайд 31

Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось
b =3)

























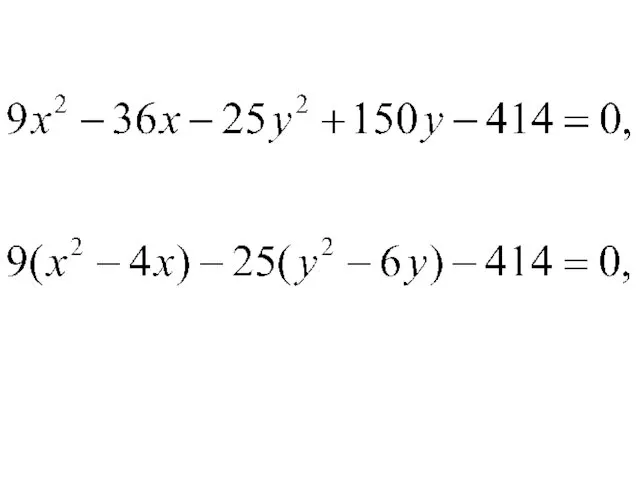
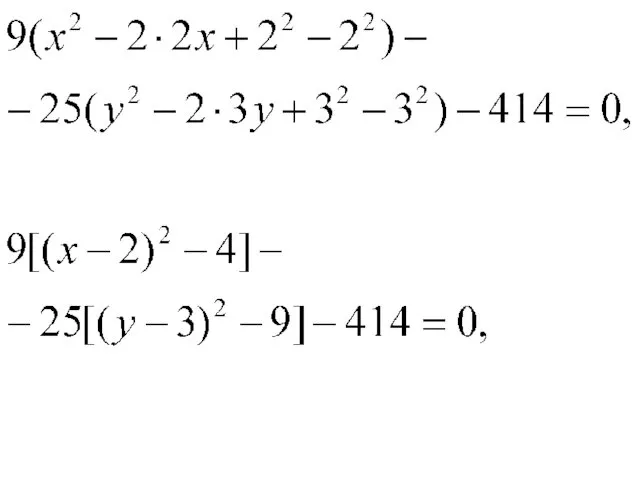
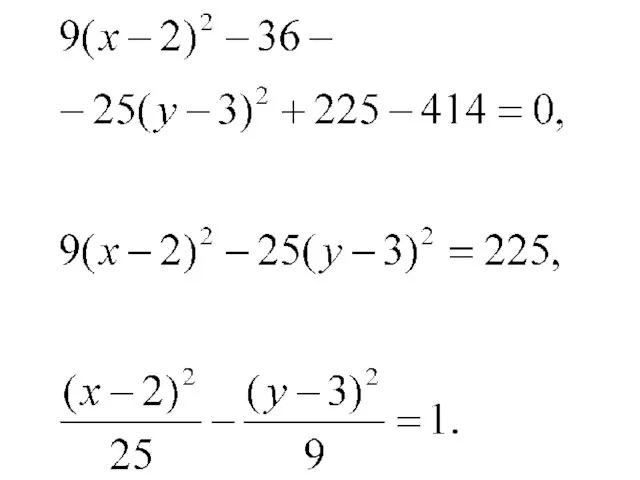


 Родительское собрание: Как воспитать уверенность ребёнка в себе
Родительское собрание: Как воспитать уверенность ребёнка в себе Ликвидация возможных аварийных ситуаций в резервуарном парке
Ликвидация возможных аварийных ситуаций в резервуарном парке Конспект открытого интегрированного занятия в подготовительной группе Путешествие в школу. Диск
Конспект открытого интегрированного занятия в подготовительной группе Путешествие в школу. Диск Болезни желудка и двенадцатиперстной кишки
Болезни желудка и двенадцатиперстной кишки Процессоры. Архитектура фон Неймана
Процессоры. Архитектура фон Неймана Наблюдения - основа астрономии
Наблюдения - основа астрономии Внеклассное мероприятие Путешествие по экологической тропе.
Внеклассное мероприятие Путешествие по экологической тропе. Паспорт комнатных растений
Паспорт комнатных растений Скульптура первой половины XIX века
Скульптура первой половины XIX века Ointments, creams and gels
Ointments, creams and gels Бойове застосування КЗА 86Ж6. Призначення та структурна схема комплексу програм КЗА 86Ж6. (Тема 8.1)
Бойове застосування КЗА 86Ж6. Призначення та структурна схема комплексу програм КЗА 86Ж6. (Тема 8.1) Урок математики во 2 классе. Квадрат
Урок математики во 2 классе. Квадрат презентация к уроку Дружба
презентация к уроку Дружба Фотоальбом
Фотоальбом ВИЧ - инфекция
ВИЧ - инфекция Правила игры и правила судейства в баскетболе
Правила игры и правила судейства в баскетболе Геодезический контроль точности выполнения СМР
Геодезический контроль точности выполнения СМР Своя игра по изобразительному искусству
Своя игра по изобразительному искусству Лекция 4 ВЕНТИЛЯЦИЯ
Лекция 4 ВЕНТИЛЯЦИЯ Строительство в г. Новый Уренгой учебного полигона. Объект строительства
Строительство в г. Новый Уренгой учебного полигона. Объект строительства Карл Павлович Брюллов (1799-1852). Итальянская тематика
Карл Павлович Брюллов (1799-1852). Итальянская тематика Соль: вред или польза?
Соль: вред или польза? Что нужно знать о ГТО
Что нужно знать о ГТО Гиперактивный ребёнок
Гиперактивный ребёнок Научное исследование, учебное исследование, проектная деятельность
Научное исследование, учебное исследование, проектная деятельность Фестиваль пасхальных посиделок
Фестиваль пасхальных посиделок Российская компания Art Lumiere. Производство и реализация декоративных элементов из гипсокартона KNAUF
Российская компания Art Lumiere. Производство и реализация декоративных элементов из гипсокартона KNAUF Элементы квантовой биофизики
Элементы квантовой биофизики