Содержание
- 2. Определение 1 Сложное высказывание называется тавтологией, если оно истинно при любых истинностных значениях входящих в него
- 3. Определение 2 Сложное высказывание называется противоречием, если оно ложно при любых истинностных значениях входящих в него
- 4. Определение 3 Сложное высказывание называется контингенцией, если оно не является ни тавтологией ни противоречием.
- 5. Пример 1 Можно построить тавтологию и противоречие, используя только одну пропозициональную переменную. Высказывание pp всегда истинно,
- 6. Два сложных высказывания называются логически эквивалентными, если они имеют одинаковые истинностные значения на всех возможных наборах
- 7. Определение 4 Сложные высказывания p и q называются логически эквивалентными, если сложное высказывание pq является тавтологией.
- 8. Для определения эквивалентности двух сложных высказываний можно использовать таблицы истинности. Будьте внимательны! В таблицах истинности, соответствующих
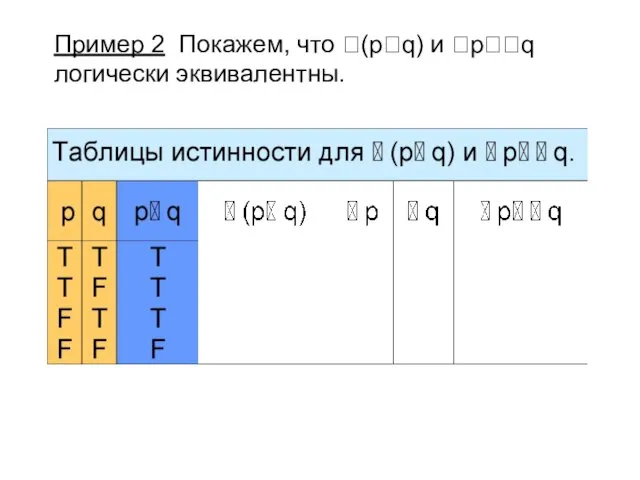
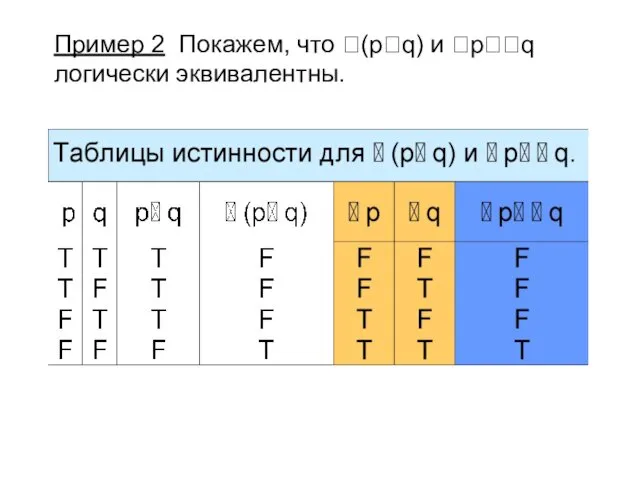
- 9. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 10. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 11. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 12. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 13. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 14. Пример 2 Покажем, что (pq) и pq логически эквивалентны.
- 15. Истинностные значения высказываний (pq) и pq совпадают на всех наборах истинностных значений переменных p и q,
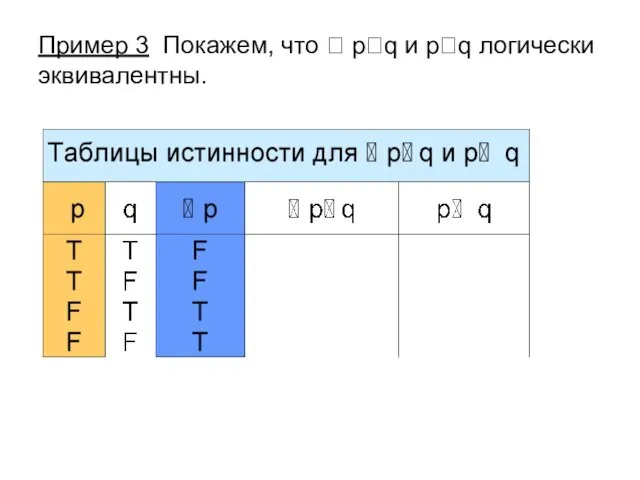
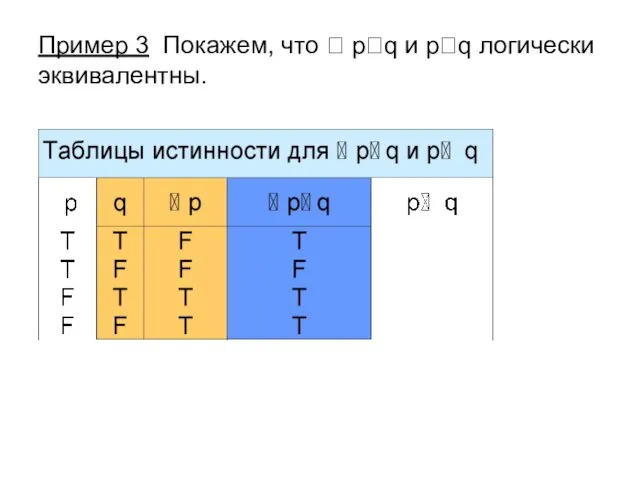
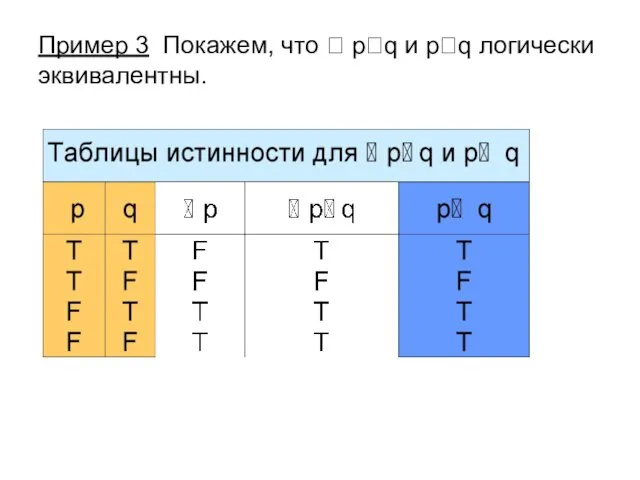
- 16. Пример 3 Покажем, что pq и pq логически эквивалентны.
- 17. Пример 3 Покажем, что pq и pq логически эквивалентны.
- 18. Пример 3 Покажем, что pq и pq логически эквивалентны.
- 19. Пример 3 Покажем, что pq и pq логически эквивалентны.
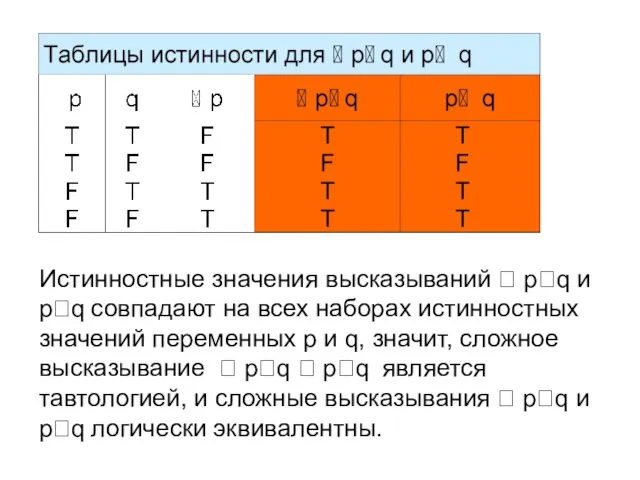
- 20. Истинностные значения высказываний pq и pq совпадают на всех наборах истинностных значений переменных p и
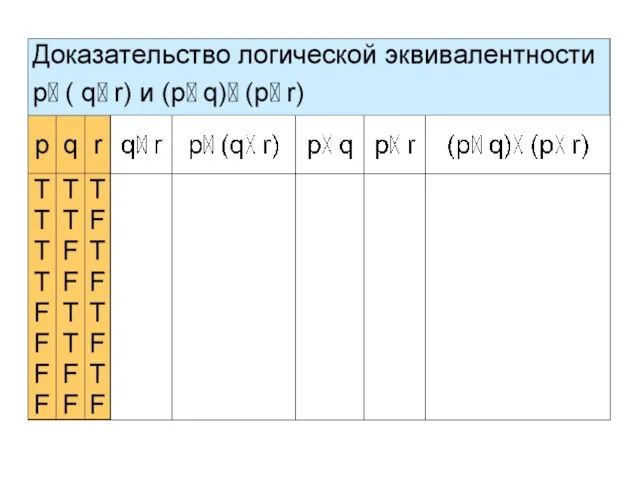
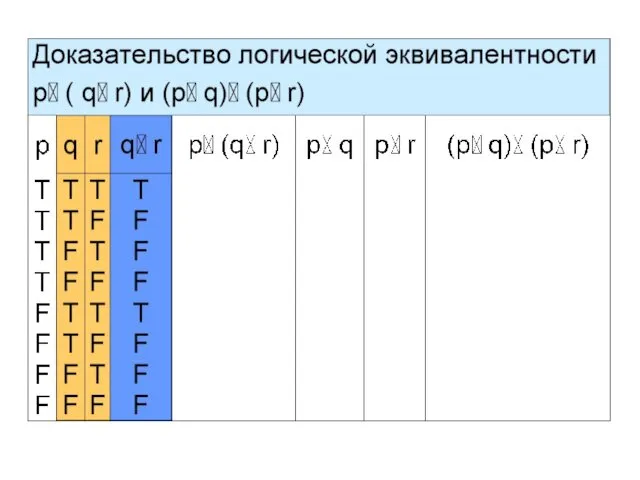
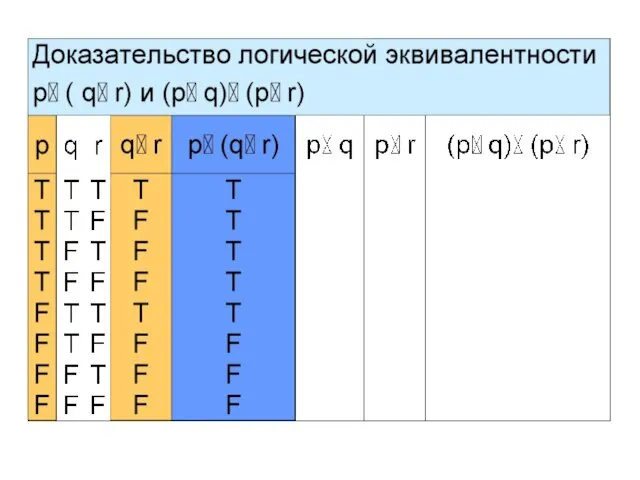
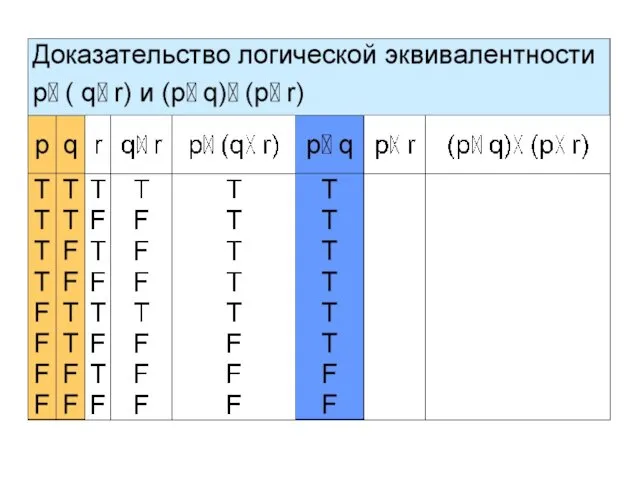
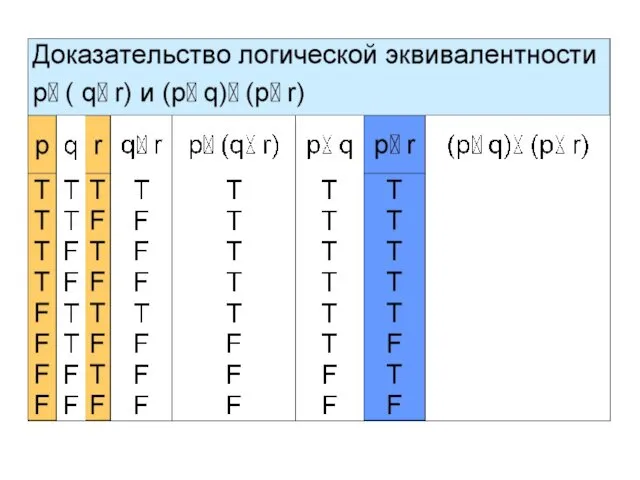
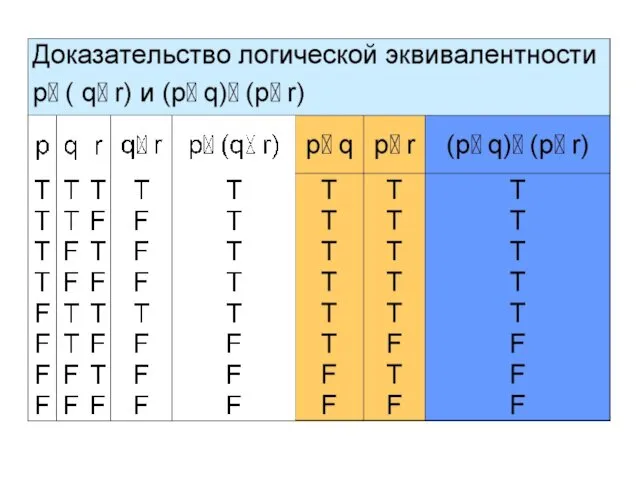
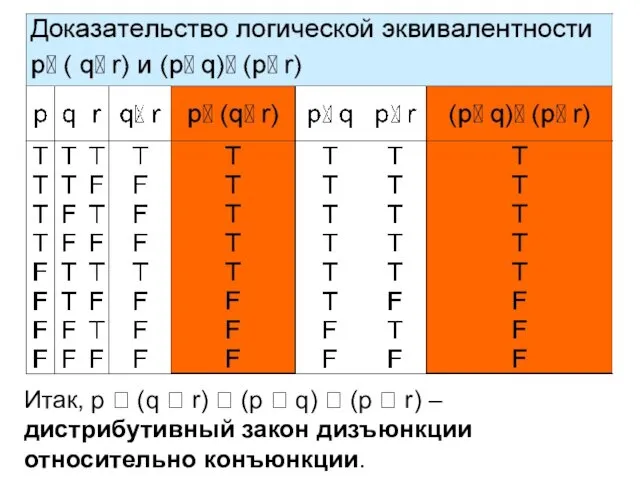
- 21. Пример 4 Покажем, что сложные высказывания p (q r) и (p q)
- 28. Итак, p (q r) (p q) (p r) – дистрибутивный
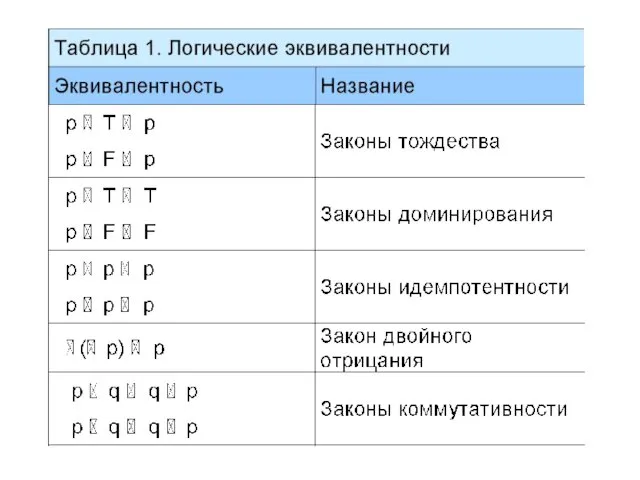
- 31. Множество сложных высказываний, на котором заданы логические операции , , , удовлетворяющие законам тождества, коммутативности, ассоциативности,
- 34. Применение законов Де Моргана Пример 5 Используем закон Де Моргана для построения отрицания высказывания: «Сергей пойдет
- 35. Применение законов Де Моргана Пример 6 Используем закон Де Моргана для построения отрицания высказывания: «У Ольги
- 36. Построение новых логических эквивалентностей Логические эквивалентности таблиц 1, 2 и 3 можно использовать для построения новых
- 37. Пример 7 Покажем с помощью преобразований, что высказывания (p q) и p q логически
- 38. Пример 7 Покажем с помощью преобразований, что высказывания (p q) и p q логически
- 39. Пример 7 Покажем с помощью преобразований, что высказывания (p q) и p q логически
- 40. Пример 8 Покажем с помощью преобразований, что высказывания (p (p q)) и (p
- 41. Пример 9 Покажем с помощью преобразований, что высказывание (p q) (p q) является
- 42. Определение 5 Сложное высказывание называется выполнимым, если существует набор истинностных значений пропозициональных переменных, на котором это
- 43. Определение 6 Набор истинностных значений пропозициональных переменных, на котором выполнимое высказывание принимает значение истина, называется решением
- 44. Пример 9 Выясним, какие из следующих высказываний являются выполнимыми: (p q) (q r)
- 45. Применения выполнимости В терминах выполнимости сложных высказываний моделируются задачи из различных областей науки и техники: робототехники,
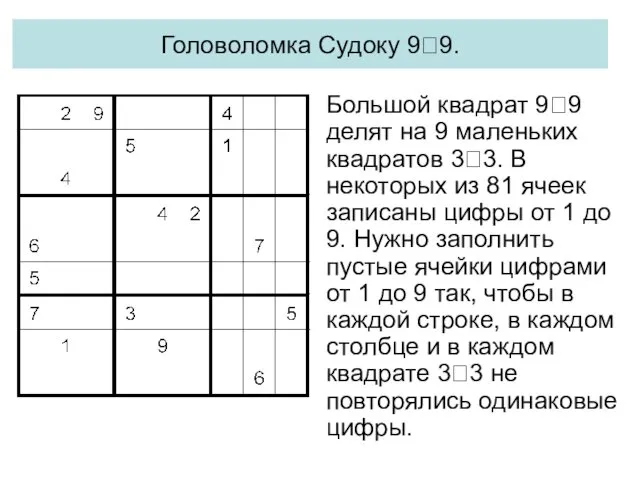
- 46. Головоломка Судоку 99. Большой квадрат 99 делят на 9 маленьких квадратов 33. В некоторых из 81
- 48. Скачать презентацию






























 Презентация мастер-класс по созданию игры Наряди ёлочку
Презентация мастер-класс по созданию игры Наряди ёлочку Present Continuous (Progressive)Tense. Настоящее длительное (продолженное) время
Present Continuous (Progressive)Tense. Настоящее длительное (продолженное) время Психологическое сопровождение речевого развития ребенка младшего дошкольного возраста.
Психологическое сопровождение речевого развития ребенка младшего дошкольного возраста. Responsibility for violation of legislation in the field of science
Responsibility for violation of legislation in the field of science Еволюція одноклiтинних і багатоклітинних організмів. Перiодизація еволюційних явищ
Еволюція одноклiтинних і багатоклітинних організмів. Перiодизація еволюційних явищ Китай: непростой путь от региональной к глобальной державе
Китай: непростой путь от региональной к глобальной державе Снятие мерок
Снятие мерок Местоимение. Теоретический материал
Местоимение. Теоретический материал Закономерности функционирования и развития систем
Закономерности функционирования и развития систем Проект Россия- родина моя
Проект Россия- родина моя Архитектурные памятники Липецкой области
Архитектурные памятники Липецкой области Безпечний інтернет
Безпечний інтернет Автоматты қайта қосылу
Автоматты қайта қосылу Мастер-класс ученика: Гиацинт.
Мастер-класс ученика: Гиацинт. Презентация Тревожные дети (диагностика, коррекция)
Презентация Тревожные дети (диагностика, коррекция) Творческий проект в школе
Творческий проект в школе Представление технологии Диск
Представление технологии Диск Системы диагностики электрооборудования и агрегаты бесперебойного питания
Системы диагностики электрооборудования и агрегаты бесперебойного питания 20230928_zvyozdnyy_chas
20230928_zvyozdnyy_chas Жизненная навигация. С кем вместе я буду идти к своей мечте?
Жизненная навигация. С кем вместе я буду идти к своей мечте? Занимательная атмосфера
Занимательная атмосфера Обучающий семинар. Инициативное бюджетирование в Пермском крае
Обучающий семинар. Инициативное бюджетирование в Пермском крае Основные требования нормативных документов ПАО Газпром по сварке при ремонте промысловых и магистральных газопроводов
Основные требования нормативных документов ПАО Газпром по сварке при ремонте промысловых и магистральных газопроводов Взаимодействие школы и семьи
Взаимодействие школы и семьи How to find a job
How to find a job Причины возникновения экстремизма и терроризма
Причины возникновения экстремизма и терроризма Предмет, объект, задачи и методы психологии
Предмет, объект, задачи и методы психологии Видобування нерудної природної сировини в Україні та країнах світу
Видобування нерудної природної сировини в Україні та країнах світу