Содержание
- 2. Математика греч. mathēmatikē от màthēma – знание, наука наука о количественных отношениях и пространственных формах действительного
- 3. Математика на педагогическом факультете Общие понятия Целые неотрицательные числа Расширение понятия числа Функции. Уравнения. Неравенства Элементы
- 4. Основная литература Стойлова, Л. П. Математика : учебное пособие для студентов сред. пед. заведений / Л.
- 5. Множества и операции над ними Понятие множества и элемента множества Способы задания множеств Отношения между множествами
- 6. Понятие множества и элемента множества Часто приходится рассматривать различные группы объектов как единое целое: … птиц
- 7. Множество – основное неопределяемое понятие математики Его поясняют на примерах. Примерами множеств могут служить: множество государств
- 8. Множества обозначают прописными буквами латинского алфавита: А, В, С, … Для некоторых множеств вводят специальные обозначения,
- 9. Множество не содержащее ни одного элемента называют пустым и обозначают символом ∅ Пример: А - множество
- 10. Объекты, из которых образовано множество, называют его элементами. Элементы множества принято обозначать строчными буквами латинского алфавита:
- 11. Множества бывают конечными и бесконечными. Примеры: 1) множество дней недели - … , 2) множество точек
- 12. Способы задания множеств Существуют два способа задания множеств. 1) перечислением всех его элементов Примеры: 1) А
- 13. 2) указанием характеристического свойства элементов множества Характеристическое свойство – свойство, которым обладают все элементы этого множества,
- 14. Примеры: 1) А – множество положительных двузначных чисел. Характеристическое свойство – «быть положительным двузначным числом». 21
- 15. Бесконечное множество можно задать лишь указанием характеристического свойства его элементов. Конечное множество можно задать двумя указанными
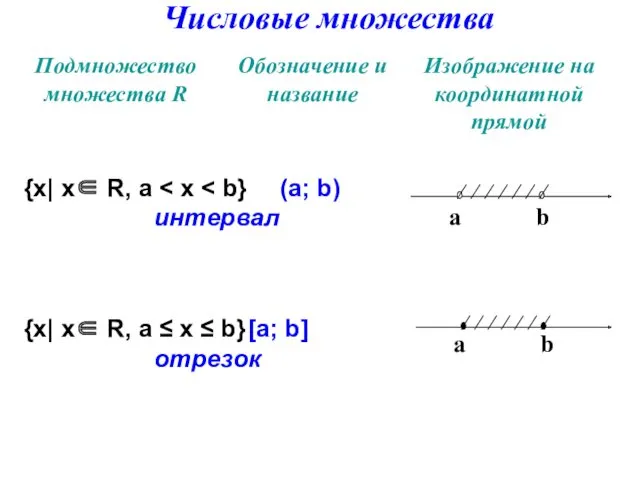
- 16. Числовые множества {х| х∈ R, а интервал {х| х∈ R, а ≤ х ≤ b} [а;
- 17. {х| х∈ R, а полуинтервал {х| х∈ R, а ≤ х полуинтервал
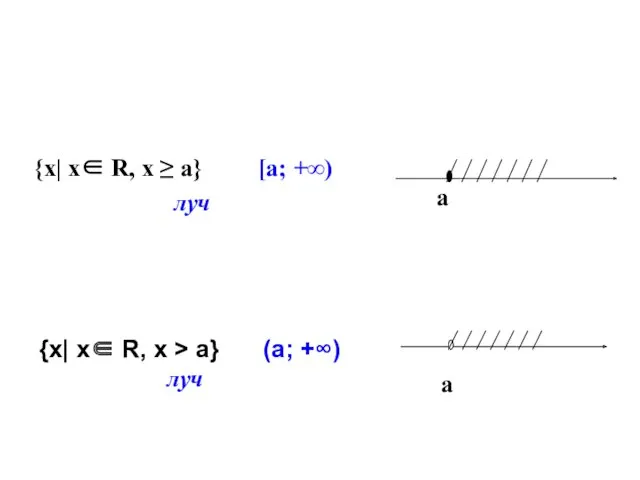
- 18. {х| х∈ R, х ≥ а} [а; +∞) луч {х| х∈ R, х > а} (а;
- 19. {х| х∈ R, х ≤ а} (- ∞; а] луч {х| х∈ R, х луч
- 20. Отношения между множествами
- 21. Отношения между множествами можно наглядно представить с помощью диаграмм Эйлера-Венна (кругов Эйлера). Множество изображается кругом на
- 22. Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то
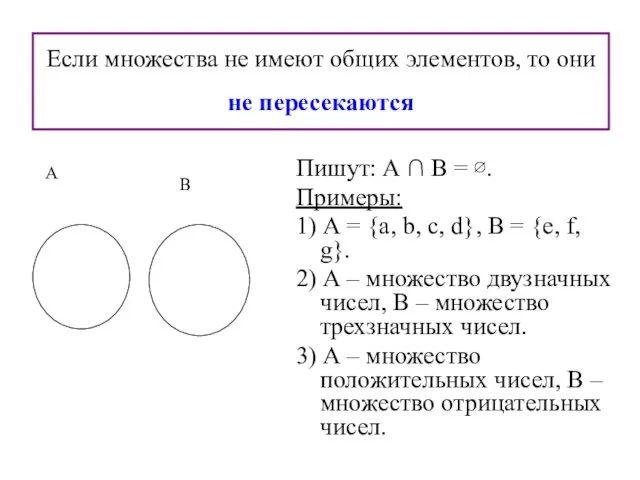
- 23. Если множества не имеют общих элементов, то они не пересекаются Пишут: А ∩ В = ∅.
- 24. Если каждый элемент множества А является элементом множества В, то говорят, что множество А включено во
- 25. Для любого множества А справедливы утверждения: 1) ∅ ⊂ А 2) А ⊂ А
- 26. Множества называют равными, если они состоят из одних и тех же элементов Примеры: 1) А =
- 27. Операции над множествами
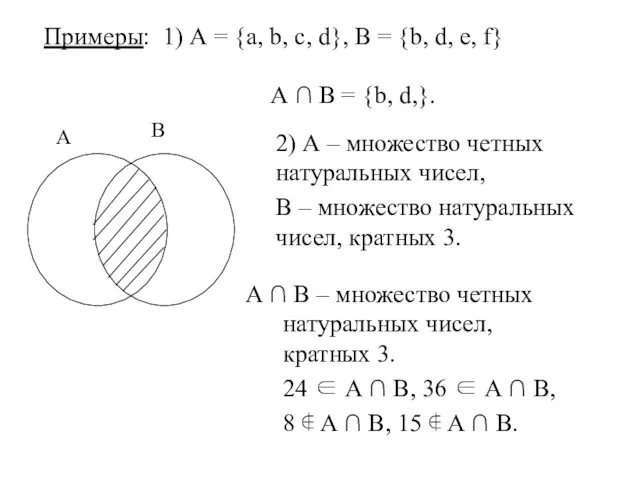
- 28. Пересечение множеств Пересечением множеств А и В называется множество А ∩ В, состоящее из тех и
- 29. Примеры: 1) А = {а, b, с, d}, В = {b, d, е, f} А ∩
- 30. 4) А – множество квадратов, В – множество прямоугольников 3) А – множество четных натуральных чисел,
- 31. Для любого множества А справедливы следующие утверждения: 1) А ∩ ∅ = ∅ 2) А ∩
- 32. х ∈ А ∩ В ⇔ х ∈ А и х ∈ В х ∉ А
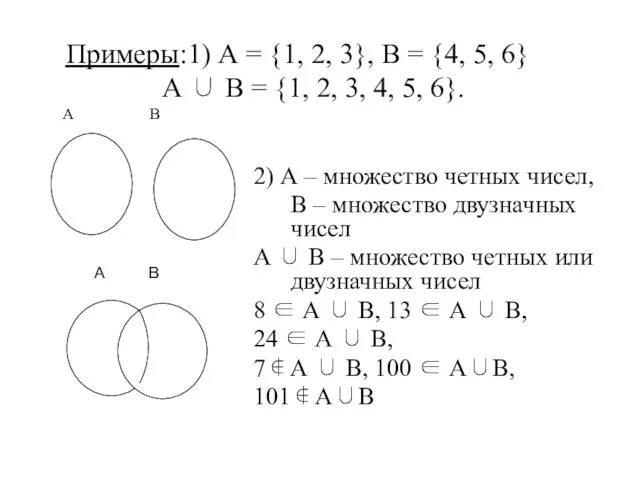
- 33. Объединение множеств Объединением множеств А и В называется множество А ∪ В, состоящее из тех и
- 34. Объединением множеств А и В называется множество А ∪ В, содержащие все элементы множества А, и
- 35. Примеры:1) А = {1, 2, 3}, В = {4, 5, 6} А ∪ В = {1,
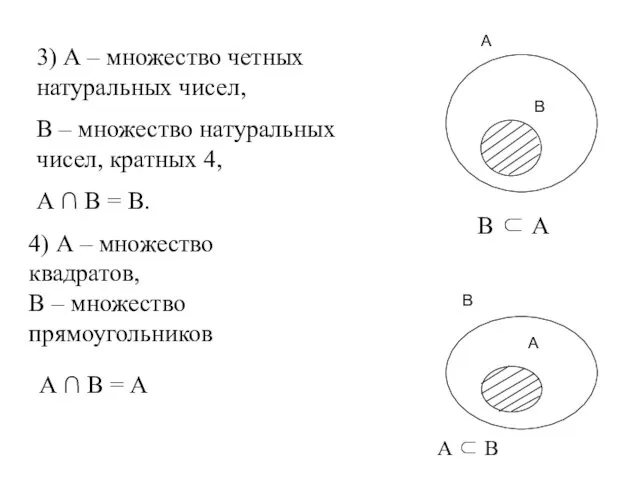
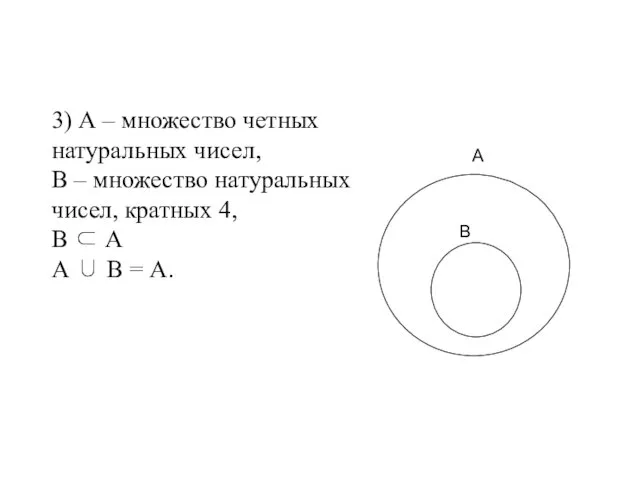
- 36. 3) А – множество четных натуральных чисел, В – множество натуральных чисел, кратных 4, В ⊂
- 37. Для любых множеств А и В справедливы следующие утверждения: 1) А ∪ ∅ = А 2)
- 38. х ∉ А ∪ В ⇔ х ∉А и х ∉ В х ∈ А ∪
- 39. Законы пересечения и объединения множеств
- 40. Операции над числами обладают рядом свойств: Например: а + b = b + а (а ·
- 41. Законы пересечения множеств 1) Коммутативный закон пересечения множеств: А ∩ В = В ∩ А Лат.
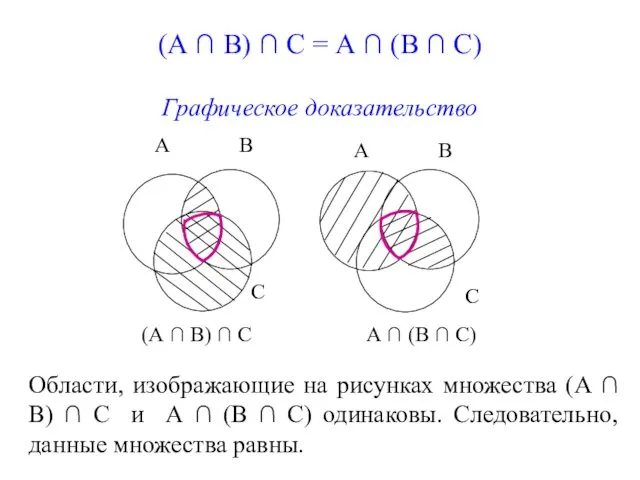
- 42. (А ∩ В) ∩ С = А ∩ (В ∩ С) Графическое доказательство А ∩ (В
- 43. Законы объединения множеств 1) Коммутативный закон объединения множеств: А ∪ В = В ∪ А 2)
- 44. 3) Дистрибутивный закон пересечения относительно объединения: (А∪В)∩С = (А∩С) ∪ (В∩С) 4) Дистрибутивный закон объединения относительно
- 45. Вычитание множеств. Дополнение подмножества
- 46. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству
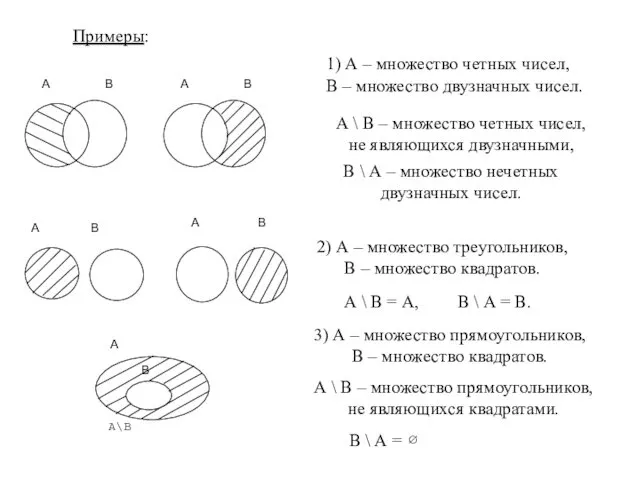
- 47. Примеры: 1) А – множество четных чисел, В – множество двузначных чисел. А \ В –
- 48. Дополнением множества В до множества А называется разность множеств А и В: В′А = А \
- 49. Примеры: 1) А = {1, 2, 3, 4, 5}, В = {1, 3, 5}. В′А =
- 50. Свойства вычитания множеств (А\В)\С = (А\С)\В (А∪В)\С = (А\С)∪(В\С) – дистрибутивность вычитания относительно объединения (А\В)∩С =
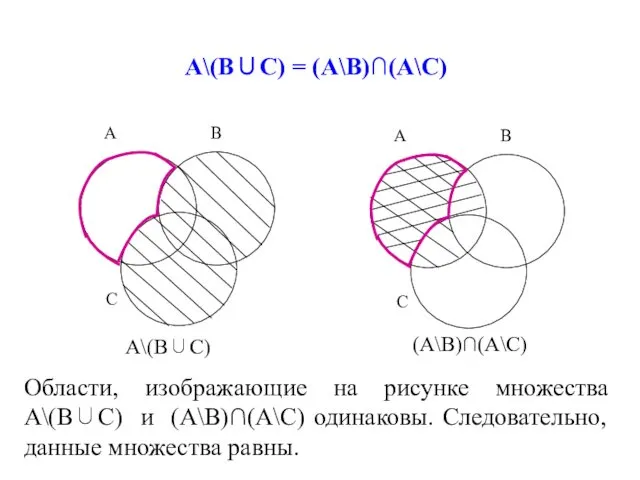
- 51. А\(В∪С) = (А\В)∩(А\С) А\(В∪С) (А\В)∩(А\С) Области, изображающие на рисунке множества А\(В∪С) и (А\В)∩(А\С) одинаковы. Следовательно, данные
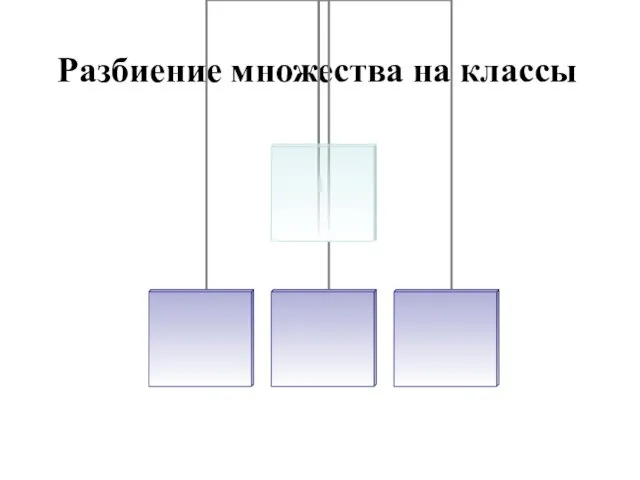
- 52. Разбиение множества на классы
- 53. Элементы некоторого множества можно распределить по классам на основании сходств элементов внутри класса и их отличия
- 54. Считают, что множество Х разбито на попарно непересекающиеся подмножества или классы Х1, Х2, …, Хn, если
- 55. Если не выполнено хотя бы одно их этих условий, классификацию считают неправильной. 2. Любые два таких
- 56. Примеры: Произошло ли разбиение множества Х на классы? или Верна ли классификация? 1. Х – множество
- 57. Разбиения множества Х на классы Х1, Х2, Х3 не получим. 2. Х – множество треугольников, Х1
- 58. Декартово умножение множеств
- 59. 2 и 7 22 27 72 77 В том случае, когда важен порядок следования элементов, в
- 60. Упорядоченные наборы элементов называют кортежами и различают по длине. Длина кортежа – это число элементов, из
- 61. Декартовым произведением множеств А и В называется множество всех упорядоченных пар, первая компонента которых принадлежит множеству
- 62. А×А = {(а; а), (а; b), (а; с), (b; а), (b; b), (b; с), (с; а),
- 63. Декартовым произведением множеств Х1, Х2, …, Хn называется множество всех кортежей длины n, первая компонента которых
- 64. (3;4;6), (3;4;7), (3;5;6), (3;5;7)}. А×В×С = {(1;4;6), (1;4;7), (1;5;6), (1;5;7), (2;4;6), (2;4;7), (2;5;6), (2;5;7), 2) А
- 65. Свойства декартова умножения 3. Дистрибутивный закон декартова умножения относительно объединения: (А∪В)×С = (А×С) ∪ (В×С) 1.
- 66. 4. Дистрибутивный закон декартова умножения относительно пересечения: (А∩В)×С = (А×С) ∩ (В×С) 5. Дистрибутивный закон декартова
- 67. График декартова произведения двух числовых множеств Примеры: Построить график декартова произведения множеств А и В. А×В={(1;3),
- 68. 2) А = [2; 5], В = {1, 3, 5} 3) А = [2; 5], В
- 69. 4) А = [2; 5], В = R 5) А = [-2; 2], В = ]2;
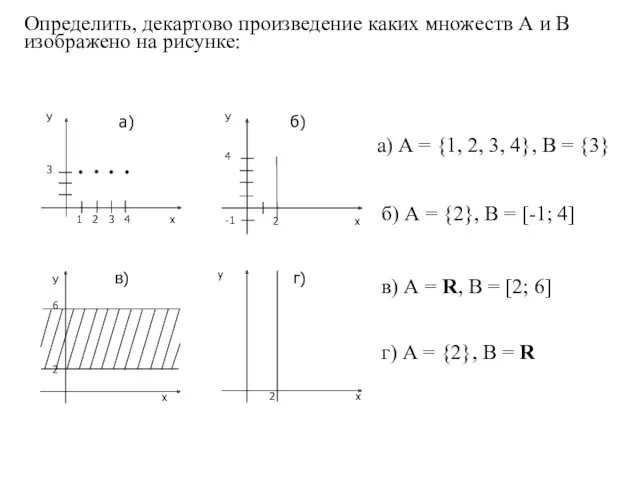
- 70. Определить, декартово произведение каких множеств А и В изображено на рисунке: а) А = {1, 2,
- 72. Скачать презентацию















![{х| х∈ R, х ≤ а} (- ∞; а] луч {х| х∈ R, х луч](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/60042/slide-18.jpg)












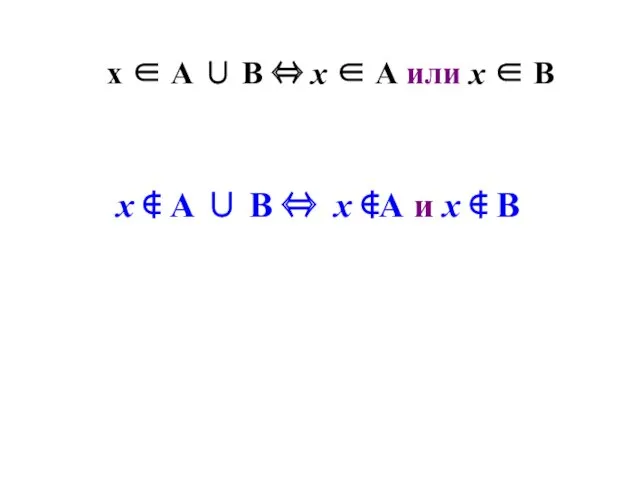

























![2) А = [2; 5], В = {1, 3, 5}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/60042/slide-67.jpg)
![4) А = [2; 5], В = R 5) А](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/60042/slide-68.jpg)
 Природные комплексы. Презентация. 6 класс
Природные комплексы. Презентация. 6 класс Хронический гастрит
Хронический гастрит Тип связи в словосочетаниях
Тип связи в словосочетаниях Проект по экспериментальной деятельности Волшебные кристаллы
Проект по экспериментальной деятельности Волшебные кристаллы Непрерывные сигналы. (Лекция 1.4)
Непрерывные сигналы. (Лекция 1.4) Влияние цены на излишек производителей
Влияние цены на излишек производителей Эпоха дворцовых переворотов
Эпоха дворцовых переворотов Науково-методичні засади організації роботи з обдарованими дітьми
Науково-методичні засади організації роботи з обдарованими дітьми Аргентина. Визитная карточка
Аргентина. Визитная карточка Презентация Малая летняя академия
Презентация Малая летняя академия Преимущества и выгода продукции Nature’s Sunshine перед аптечными аналогами
Преимущества и выгода продукции Nature’s Sunshine перед аптечными аналогами Информационные жанры. Как писать заметку
Информационные жанры. Как писать заметку Поздравляем с 23 февраля
Поздравляем с 23 февраля Воспитательный потенциал современной семьи
Воспитательный потенциал современной семьи Площади подобных фигур
Площади подобных фигур Вентиляция помещений
Вентиляция помещений Презентация Шоколад
Презентация Шоколад Международный день охраны памятников и исторических мест
Международный день охраны памятников и исторических мест Симплекс-метод
Симплекс-метод содержание работы по развитию слухового восприятия речи
содержание работы по развитию слухового восприятия речи Внеурочная деятельность Мои первые проекты. тема Декупаж
Внеурочная деятельность Мои первые проекты. тема Декупаж Направления реализации Национальной стратегии по обращению с ТКО и ВМР
Направления реализации Национальной стратегии по обращению с ТКО и ВМР 2.2. Элементарные действия. Алгоритмические структуры [ТРИК]
2.2. Элементарные действия. Алгоритмические структуры [ТРИК] Презентация к занятию по предшкольной подготовке Снеговик - почтовик
Презентация к занятию по предшкольной подготовке Снеговик - почтовик Этнос и этничность в российской этнологии. Признаки этноса – факторы актуализации этничности
Этнос и этничность в российской этнологии. Признаки этноса – факторы актуализации этничности Патофизиология: предмет, задачи, методы
Патофизиология: предмет, задачи, методы Ассортимент курток FW 19-20
Ассортимент курток FW 19-20 Робототехника. Понятие, история и современность
Робототехника. Понятие, история и современность