Содержание
- 2. 03.10.2019 Лекция № 5 1. Модель гармонического осциллятора. Свободные незатухающие колебания. 1.1. Основное уравнение движения 1.2.
- 3. 03.10.2019 Колеба́ния — это повторяющийся во времени процесс, в ходе которого система изменяет свое состояние около
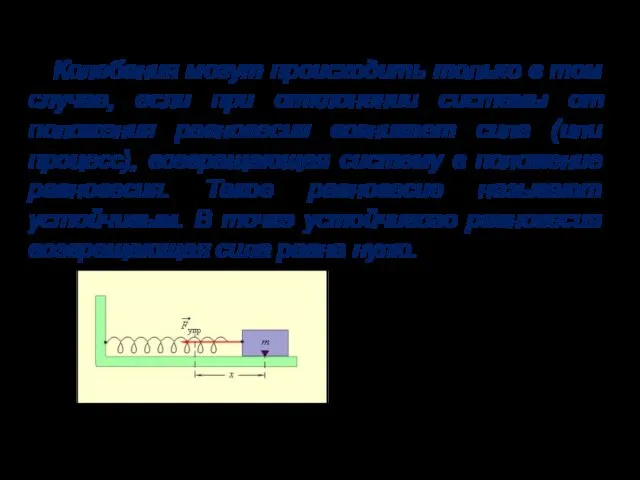
- 4. 03.10.2019 Колебания могут происходить только в том случае, если при отклонении системы от положения равновесия возникает
- 5. 03.10.2019 Модель гармонического осциллятора. Свободные незатухающие колебания. Колебания называются свободными (или собственными), если они совершаются за
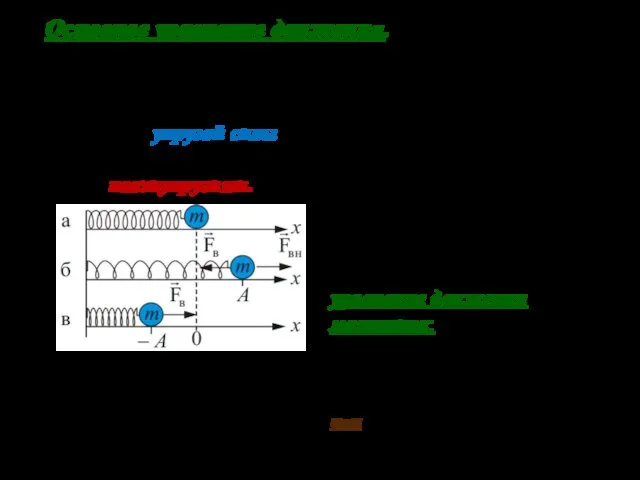
- 6. 03.10.2019 Основное уравнение движения. В качестве конкретного примера рассмотрим груз массой m, прикрепленный абсолютно упругой пружиной
- 7. 03.10.2019 Обозначим Получим основное уравнение динамики гармонических колебаний, вызываемых упругими силами: Уравнение, содержащее производные, называют дифференциальным
- 8. 03.10.2019 - амплитудой колебания, максимальное значение колеблющейся величины, величина неотрицательная, - круговая (циклическая) частота, - фаза
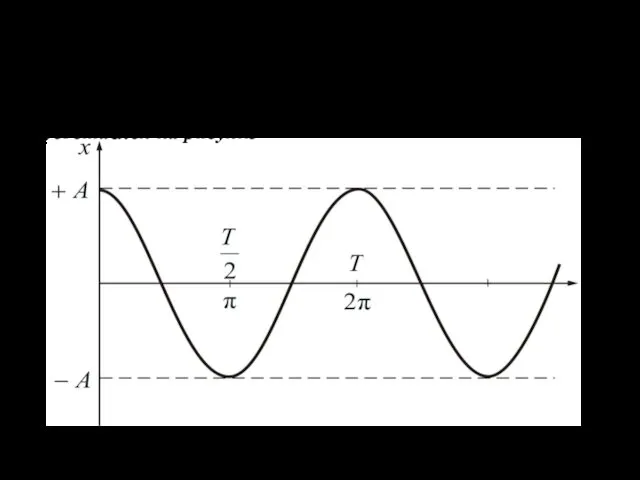
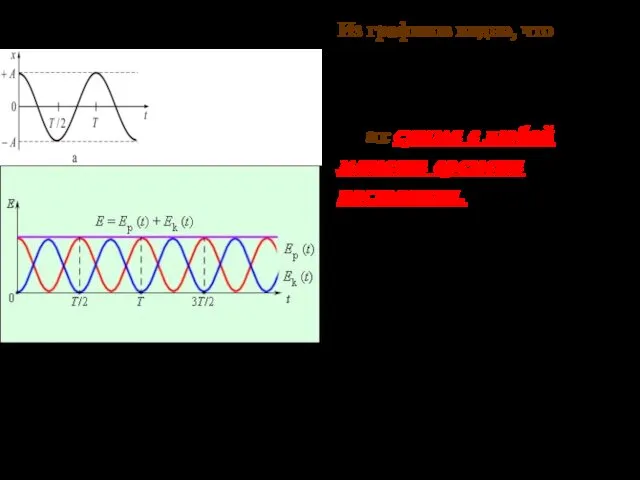
- 9. 03.10.2019 График этой функции для случая = 0 представлен на рисунке время фаза
- 10. 03.10.2019 Состояние системы, совершающей гармонические колебания, повторяется через промежуток времени Т, называемый периодом колебаний. За один
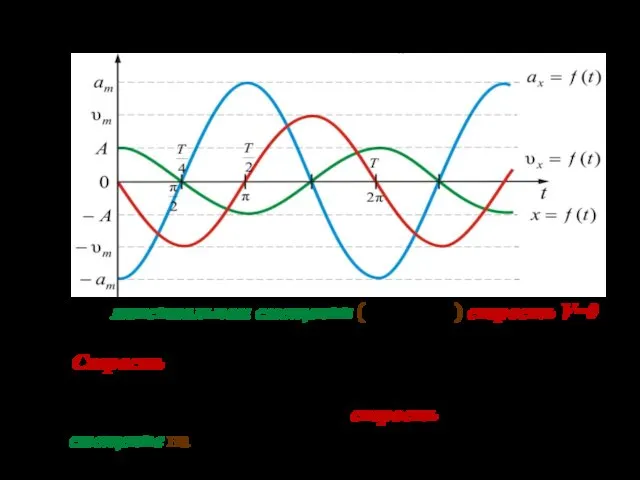
- 11. 03.10.2019 Скорость и ускорение в колебательном процессе Согласно определению, первая производная от по времени является скоростью:
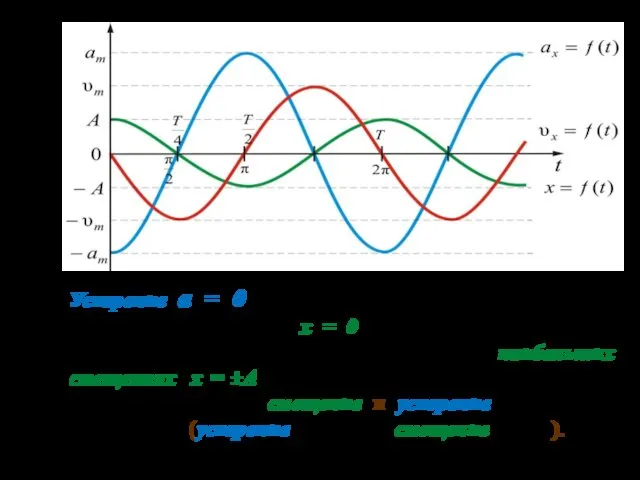
- 12. 03.10.2019 Рассмотрим графики , , При максимальном смещении ( ) скорость V=0 Скорость колебаний тела максимальна
- 13. 03.10.2019 Ускорение a = 0 равно нулю при прохождении телом положения равновесия (x = 0) и
- 14. 03.10.2019 Энергия гармонических колебаний складывается из кинетической энергии движения и потенциальной энергии в поле упругой силы
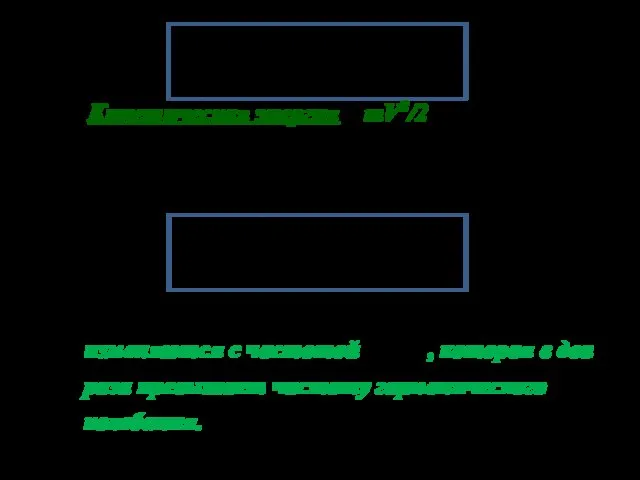
- 15. 03.10.2019 или Кинетическая энергия mV2/2 или Из формул, приведенных в рамках следует, что U и K
- 16. 03.10.2019 Сложив выражения для U и K, получим формулу для полной энергии: Полная энергия остается постоянной,
- 17. 03.10.2019 Из графиков видно, что происходит переход кинетической энергии в потенциальную и наоборот, но их сумма
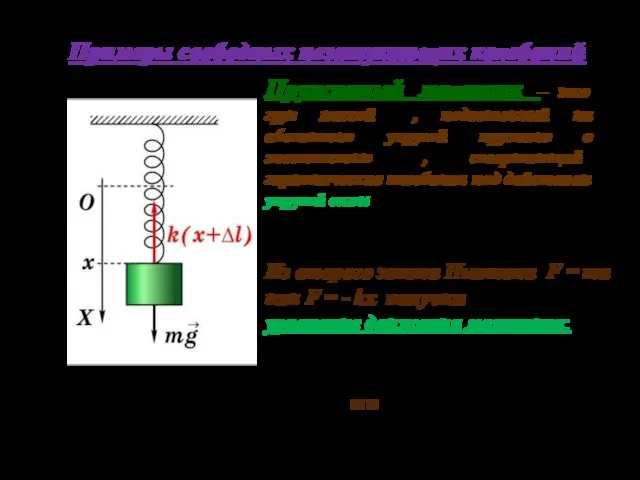
- 18. 03.10.2019 Примеры свободных незатухающих колебаний Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой
- 19. 03.10.2019 Решение этого уравнения – гармонические колебания вида: циклическая частота период
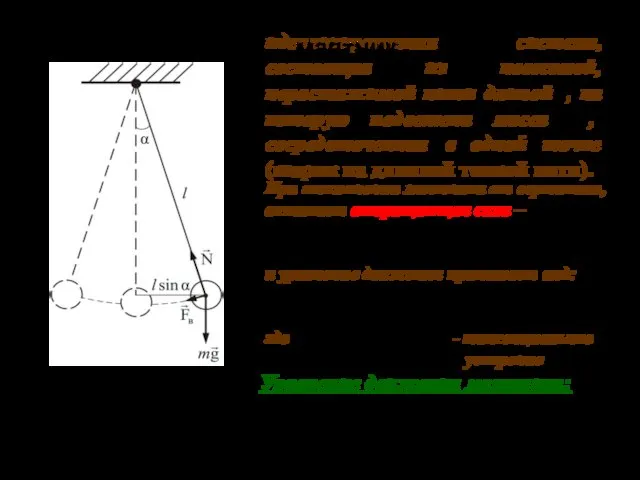
- 20. 03.10.2019 идеализированная система, состоящая из невесомой, нерастяжимой нити длиной l, на которую подвешена масса m, сосредоточенная
- 21. 03.10.2019 Так как рассматриваются только малые отклонения ( ), уравнение движения маятника можно упростить Решением этого
- 22. 03.10.2019
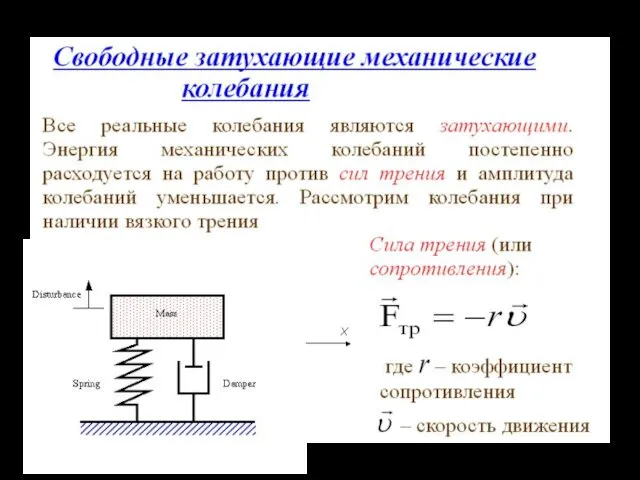
- 23. 03.10.2019 Второй закон Ньютона для затухающих колебаний вдоль оси x примет вид : где kx –
- 24. 03.10.2019 Дифференциальное уравнение свободных затухающих колебаний: Решение этого уравнения (при δ Частота колебаний: Период:
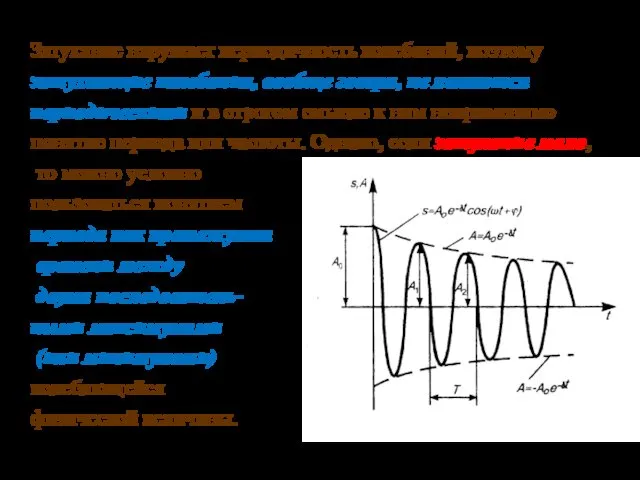
- 25. 03.10.2019 Затухание нарушает периодичность колебаний, поэтому затухающие колебания, вообще говоря, не являются периодическими и в строгом
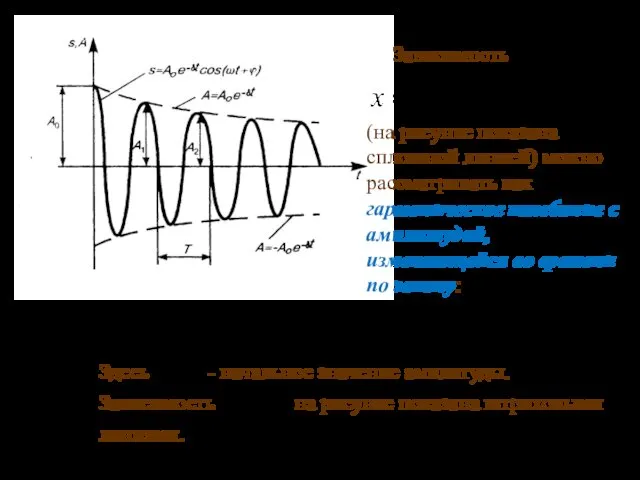
- 26. 03.10.2019 Зависимость (на рисунке показана сплошной линией) можно рассматривать как гармоническое колебание с амплитудой, изменяющейся во
- 27. 03.10.2019 Основные параметры (характеристики) затухающих колебаний Время релаксации - τ - время, за которое амплитуда уменьшается
- 28. 03.10.2019 Логарифмическим декрементом затухания d называется натуральный логарифм отношения амплитуд, следующих друг за другом через период
- 29. 03.10.2019 Добротность является важнейшей характеристикой колебательной системы, которая при малых значениях коэффициента затухания равна Добротность обратна
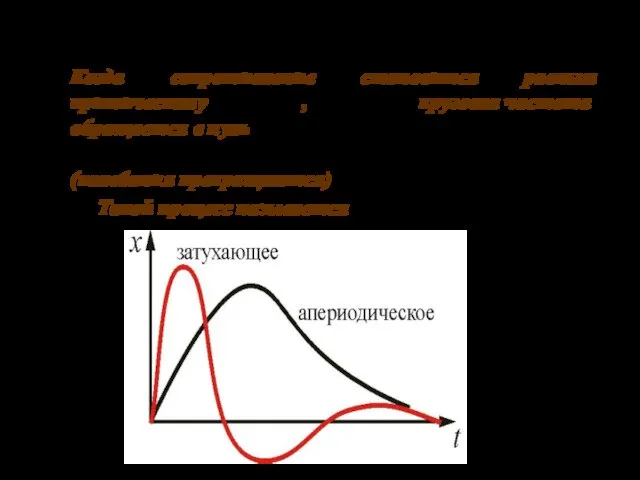
- 30. 03.10.2019 Когда сопротивление становится равным критическому , круговая частота обращается в нуль (колебания прекращаются) Такой процесс
- 31. 03.10.2019 Отличия апериодического процесса от рассмотренных затухающих колебаний в следующем. При колебаниях, тело, возвращающееся в положении
- 32. 03.10.2019 Вынужденные колебания гармонического осциллятора Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери
- 33. 03.10.2019 Дифференциальное уравнение вынужденных колебаний под действием гармонической силы Рассмотрим систему, на которую кроме упругой силы
- 34. 03.10.2019 Решение этого уравнения в общем случае имеет сложный вид, но для t >> 1/δ решение
- 35. 03.10.2019 Видно, что амплитуда колебаний имеет максимум при некоторой частоте, которую называют резонансной Чтобы определить резонансную
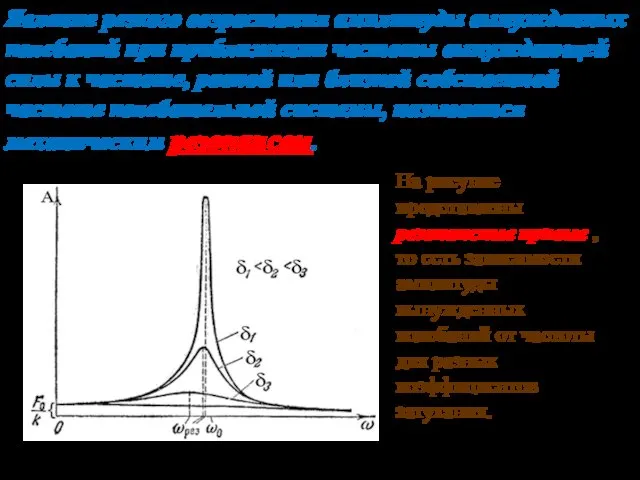
- 36. 03.10.2019 Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или
- 37. 03.10.2019 При малом затухании: Разделим полученную резонансную амплитуду на статическое смещение системы из положения равновесия под
- 39. Скачать презентацию



















 Шаблон курсового проекта
Шаблон курсового проекта Использование ИКТ в образовательном пространстве ДОУ
Использование ИКТ в образовательном пространстве ДОУ Тема: Здоровый образ жизни.
Тема: Здоровый образ жизни. Волоховой
Волоховой Реконструкция подстанции 110/10 кВ с разработкой релейной защиты силового трансформатора
Реконструкция подстанции 110/10 кВ с разработкой релейной защиты силового трансформатора Программа по внеурочной деятельности пректного направления Мой родной край
Программа по внеурочной деятельности пректного направления Мой родной край Презентация Виды работы с текстом учебника географии
Презентация Виды работы с текстом учебника географии Лучевая диагностика туберкулеза органов дыхания
Лучевая диагностика туберкулеза органов дыхания Презентация Механизм взаимодействия учителя-логопеда с педагогом-психологом и социальным педагогом в рамках деятельности ПМПконсилиума общеобразовательной организации
Презентация Механизм взаимодействия учителя-логопеда с педагогом-психологом и социальным педагогом в рамках деятельности ПМПконсилиума общеобразовательной организации Презентация к уроку 70 лет со дня освобождения Кубани от фашистских захватчиков
Презентация к уроку 70 лет со дня освобождения Кубани от фашистских захватчиков презентация к уроку Географическое положение Африки
презентация к уроку Географическое положение Африки Первоклассник
Первоклассник Под знаком двойной розы. Англия при Тюдорах
Под знаком двойной розы. Англия при Тюдорах презентацияАзбука нравственности
презентацияАзбука нравственности Вторая Мировая война. Тихоокеанский фронт
Вторая Мировая война. Тихоокеанский фронт Рождение протестантизма православия
Рождение протестантизма православия Витамин В-12. Дефицитная анемия
Витамин В-12. Дефицитная анемия Природные зоны Австралии
Природные зоны Австралии Сити-фермер - профессия будущего
Сити-фермер - профессия будущего Зажимные устройства технологической оснастки и их расчёт
Зажимные устройства технологической оснастки и их расчёт Химический состав клетки. (9 класс)
Химический состав клетки. (9 класс) бизнес план
бизнес план Саул. Царственные задатки и непослушание, гордость, зависть
Саул. Царственные задатки и непослушание, гордость, зависть Центральная и осевая симметрии презентации по геометрии для 8АВ
Центральная и осевая симметрии презентации по геометрии для 8АВ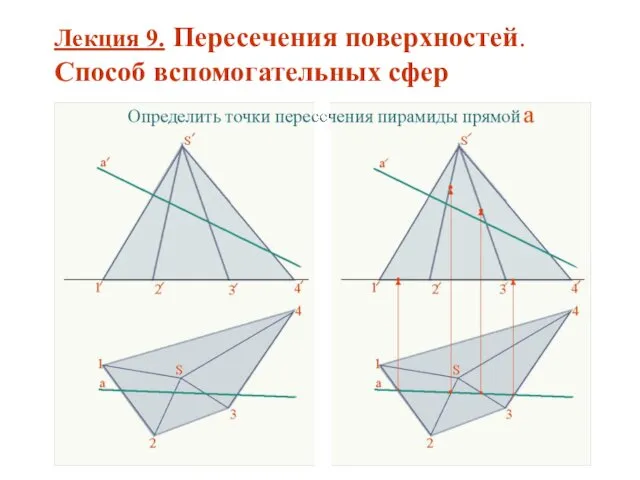 Пересечения поверхностей. Способ вспомогательных сфер. (Лекция 9)
Пересечения поверхностей. Способ вспомогательных сфер. (Лекция 9) Атлас педагогических идей
Атлас педагогических идей Слесарное дело. Тест
Слесарное дело. Тест Век медный, бронзовый, железный. Презентация к уроку химии 9 класс.
Век медный, бронзовый, железный. Презентация к уроку химии 9 класс.