Содержание
- 2. Для решения линейных и квадратных неравенств в 9 классе рассматриваются следующие приемы решения данных неравенств, данные
- 3. 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком (не
- 4. Например. Решить неравенство
- 5. Неравенство равносильно неравенству член перенесли из правой части неравенства в левую с противоположным знаком.
- 6. 2. Обе части неравенства можно умножить или разделить на одно и тоже положительное число, не меняя
- 7. Например. Решить неравенство
- 8. Неравенство равносильно Неравенству обе части первого неравенства разделили на положительное число 4
- 9. 3. Обе части неравенства можно умножить и разделить на одно и тоже отрицательное число, заменив при
- 10. Например. Решить неравенство
- 11. Неравенство равносильно Неравенству обе части первого неравенства умножили на отрицательное число -1, изменив при этом знак
- 12. Рассмотренные правила 2 и 3 допускают обобщения (соответствующие утверждения представляют собой теоремы) Теорема 1. Если обе
- 13. Например. Решить неравенство неравенство равносильно неравенству (обе части исходного неравенства умножили на выражение ( ), отрицательное
- 14. Теорема 2. Если обе части неравенства с переменной x умножить или разделить на одно и тоже
- 15. Например. Решить неравенство неравенство равносильно неравенству X+7>0 (обе части исходного неравенства разделили на выражение , положительное
- 16. Рациональные неравенства. При решении рациональных неравенств используются те приемы, которые были рассмотрены выше. С помощью этих
- 17. Метод интервалов Сущность метода интервалов заключается в следующем: ввести функцию; найти область определения; найти нули функции;
- 18. Например. Решить неравенство
- 19. Ввели функцию D (f)= R/{3} 3. Нули функции: x=1; X=-2 4-5. 6. F (x)>0 ⬄ 7.
- 20. Система неравенств Задача. Задумано натуральное число. Известно, что если к квадрату задуманного числа прибавить 13, то
- 21. Решение. Первый этап. Составление математической модели. Пусть x – задуманное число. По первому условию сумма чисел
- 23. Второй этап. Работа с составленной моделью. Преобразуем первое неравенство к виду: Найдем корни трехчлена С помощью
- 24. Преобразуем, второе неравенство системы и приведем к виду Найдем корни трехчлена С помощью параболы делаем вывод,
- 25. Третий этап. Ответ на вопрос задачи. Нас интересует натуральное число, принадлежащее интервалу (13, 15). Таким числом
- 26. Метод парабол неравенство преобразуется к виду находятся корни квадратного трехчлена x1,x2; парабола, служащая графиком функции пересекает
- 27. Например. Решить неравенство 1. 2. 3.
- 28. 4. y Ответ:
- 29. Системы уравнений Метод подстановки Суть данного метода заключается в следующем: выражается y через x из одного
- 30. Система уравнений Метод алгебраического сложения. Суть метода решения данного уравнения учащиеся рассматривается в 7 классе, где
- 32. Скачать презентацию




















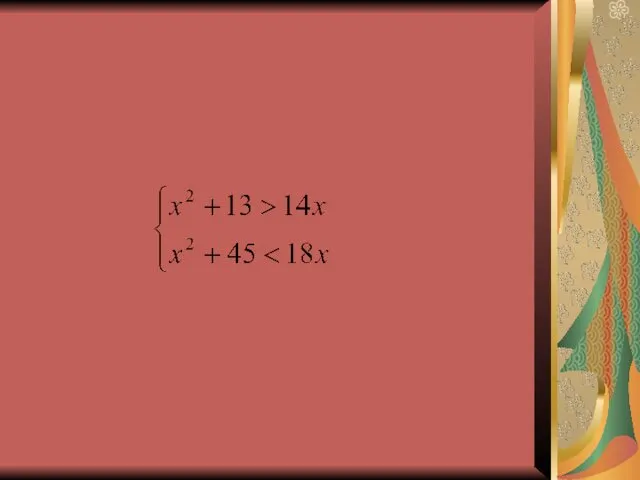








 Урок 30
Урок 30 Б английский 13.04
Б английский 13.04 Вредные советы Оратору. Юмористически-познавательная работа для всех кто выступает с презентациями
Вредные советы Оратору. Юмористически-познавательная работа для всех кто выступает с презентациями Психологические модели интеллектуальных способностей
Психологические модели интеллектуальных способностей Германия и дизайн. Послевоенное время
Германия и дизайн. Послевоенное время Презентация Текстильные бусы
Презентация Текстильные бусы Фрагмент текста. Операции над фрагментами
Фрагмент текста. Операции над фрагментами Путешествие на остров Кижи в день праздника Преображения Господня
Путешествие на остров Кижи в день праздника Преображения Господня Пермская и Кунгурская епархия РПЦ Добрянское благочиние. Храм св.апостола Иоанна Богослова
Пермская и Кунгурская епархия РПЦ Добрянское благочиние. Храм св.апостола Иоанна Богослова Иррациональные уравнения
Иррациональные уравнения урок творчесва веер
урок творчесва веер МИНИ МУЗЕЙ В ГРУППЕ РАННЕГО ВОЗРАСТА ТЕМА № 3 ИГРУШКИ А. БАРТО Диск
МИНИ МУЗЕЙ В ГРУППЕ РАННЕГО ВОЗРАСТА ТЕМА № 3 ИГРУШКИ А. БАРТО Диск Презентация к открытому занятию Подарок от сердца
Презентация к открытому занятию Подарок от сердца Правовые отношения
Правовые отношения Рациональные числа. Урок обобщение и систематизации знаний
Рациональные числа. Урок обобщение и систематизации знаний Введение в изучение обществознания в 7 классе
Введение в изучение обществознания в 7 классе Оборудование предприятий торговли. Транспортирующие машины периодического и непрерывного действия
Оборудование предприятий торговли. Транспортирующие машины периодического и непрерывного действия Технология возведения кирпичных зданий
Технология возведения кирпичных зданий Таблица сложения. 1 класс
Таблица сложения. 1 класс Устройства плавного пуска
Устройства плавного пуска poeziya-zhenskoy-dushi--
poeziya-zhenskoy-dushi-- Írsko. Geografická poloha
Írsko. Geografická poloha Список международных конференций на весенний семестр 2016 года
Список международных конференций на весенний семестр 2016 года Николай Алексеевич Некрасов и музыка
Николай Алексеевич Некрасов и музыка Технологический подход к обучению как процесс поиска построения эффективного процесса обучения
Технологический подход к обучению как процесс поиска построения эффективного процесса обучения Августовский педагогический совет. Анализ работы школы за 2017-2018 учебный год. Задачи на 2018-2019 учебный год
Августовский педагогический совет. Анализ работы школы за 2017-2018 учебный год. Задачи на 2018-2019 учебный год Презентация без названия (7)
Презентация без названия (7) Булгаков Михаил Афанасьевич
Булгаков Михаил Афанасьевич