Многогранники. Геометрические понятия презентация

Многогранники
Тетраэдр
Параллелепипед

Геометрические понятия
Плоскость – грань
Прямая – ребро
Точка – вершина
грань
ребро
вершина

Определение сечения.
Секущей плоскостью многогранника называется…
Сечением многогранника называется …

Сечением поверхности
геометрических тел называется
плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости

сечение

Плоскость
(в том числе и секущую) можно задать
следующим
образом

Секущая плоскость
А
В
С
D
M
N
K
α

Секущая плоскость
сечение
A
B
C
D
M
N
K
α

Секущая плоскость пересекает грани многогранника по прямым, а точнее по отрезкам - разрезам.
Так как секущая плоскость идет непрерывно, то разрезы образуют замкнутую фигуру-многоугольник.
Полученный таким образом многоугольник и будет сечением тела.

Демонстрация сечений

P
N
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
В
С
D
P
M
N
2. Отрезок PN
А
В
С
D
M
L 1. Отрезок MP
Построение:
3. Отрезок MN
MPN – искомое сечение
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение

Аксиоматический метод
Метод следов
Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .

Построить сечение тетраэдра плоскостью, заданной тремя точками.
Метод …
Построение:
А
С
В
D
N
P
Q
R
E
1. Отрезок NQ
2. Отрезок NP
Прямая NP пересекает АС в точке Е
3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение

Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
B
C
D
M
N
P
X
K
S
L
1. MN; отрезок МК
2. MN пересекает АВ в точке Х
3. ХР; отрезок SL
MKLS – искомое сечение

XY – след секущей плоскости
на плоскости основания
D
C
B
Z
Y
X
M
N
P
S
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
А
F

Когда метод следов не нужен

Когда метод следов не нужен
Найти площадь сечения, проведённого
Через середины рёбер при одной вершине, если ребро куба а см.

Задача 3. Построить сечение плоскостью, проходящей через точки К, L, М.
К
L
М
Построение:
1. ML
2. ML ∩ D1А1 = E
3. EK
МLFKPG – искомое сечение
F
E
N
P
G
T
4. EK ∩ А1B1 = F
6. LM ∩ D1D = N
5. LF
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK

Пояснения к построению:
1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1.
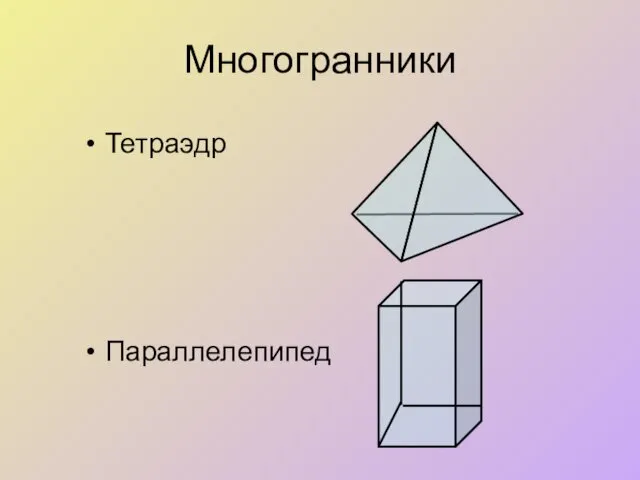
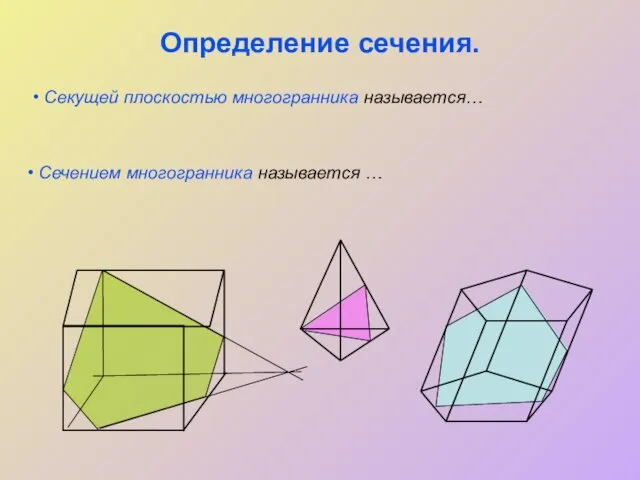
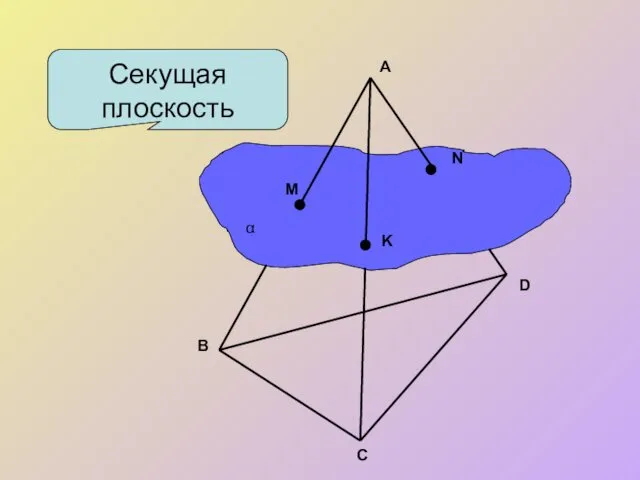
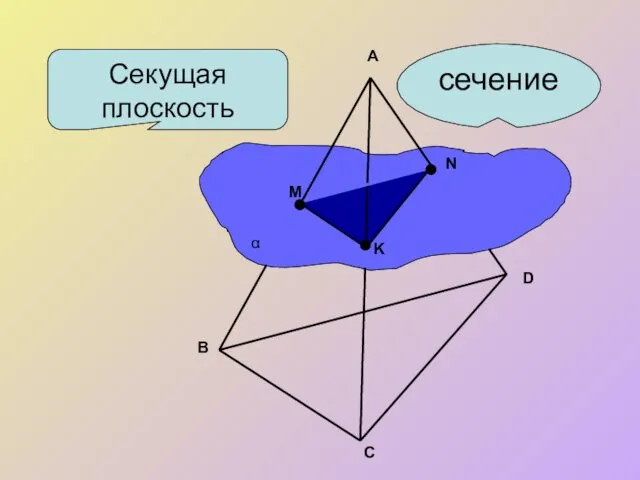
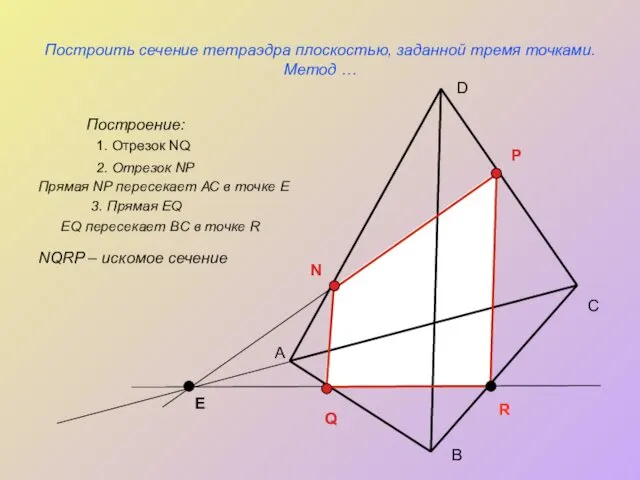
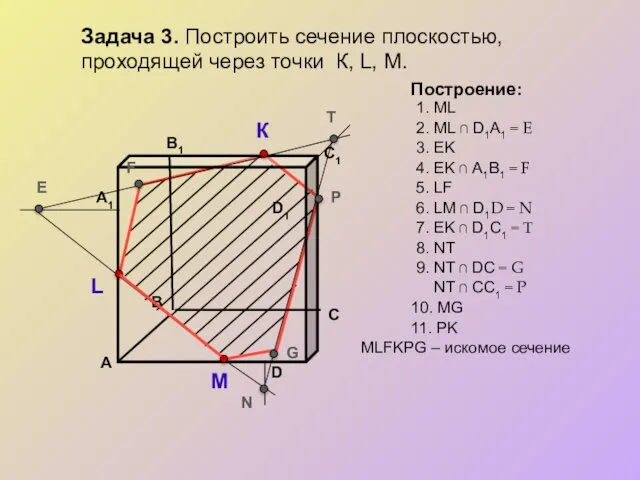
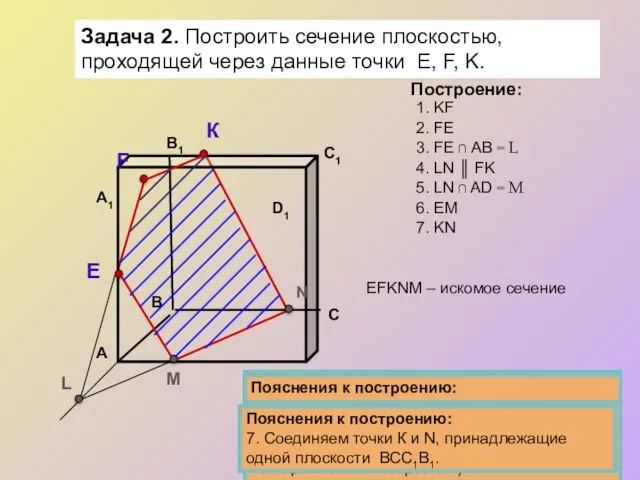
Задача 2. Построить сечение плоскостью, проходящей через данные точки Е, F, K.
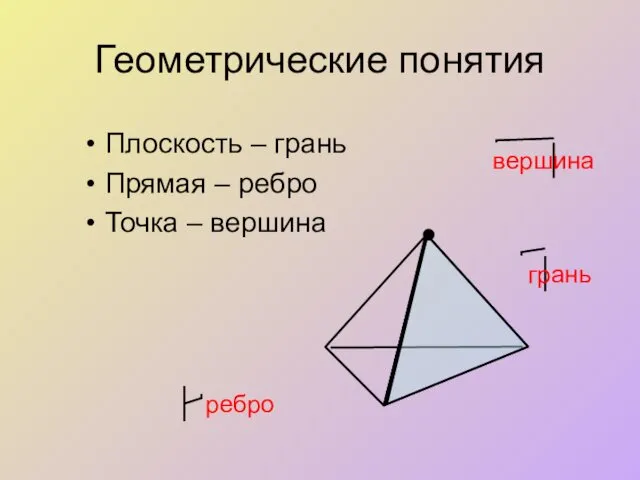
К
L
М
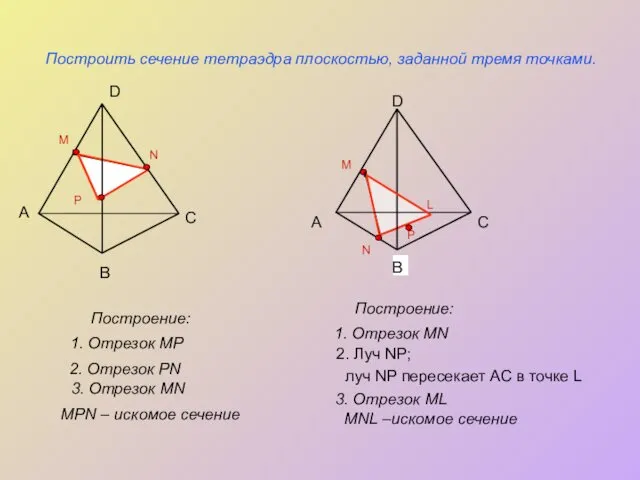
Построение:
1. KF
2. FE
3. FE ∩ АB = L
EFKNM – искомое сечение
F
E
N
4. LN ║ FK
6. EM
5. LN ∩ AD = M
7. KN
Пояснения к построению:
2. Соединяем точки F и E, принадлежащие одной плоскости АА1В1В.
Пояснения к построению:
3. Прямые FE и АВ, лежащие в одной плоскости АА1В1В, пересекаются в точке L .
Пояснения к построению:
4. Проводим прямую LN параллельно FK (если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам).
Пояснения к построению:
5. Прямая LN пересекает ребро AD в точке M.
Пояснения к построению:
6. Соединяем точки Е и М, принадлежащие одной плоскости АА1D1D.
Пояснения к построению:
7. Соединяем точки К и N, принадлежащие одной плоскости ВСС1В1.

Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
M
A
1)
1)
2)
2)
В
С
К
В
A
С
E
F
H
E
H
F
1 вариант
2 вариант
D
C
B
M
N
P
А
F
D
C
B
M
N
P
А
F