Содержание
- 2. Непрерывные случайные величины Примеры: артериальное давление пациента; масса тела пациента; - скорость биохимической реакции в клетке.
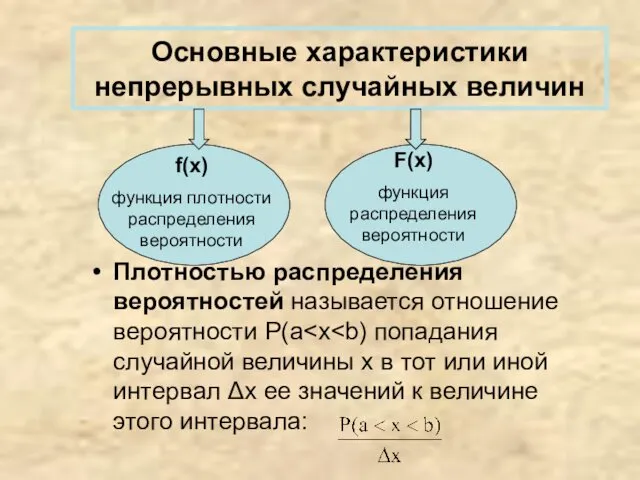
- 3. Основные характеристики непрерывных случайных величин Плотностью распределения вероятностей называется отношение вероятности Р(a f(x) функция плотности распределения
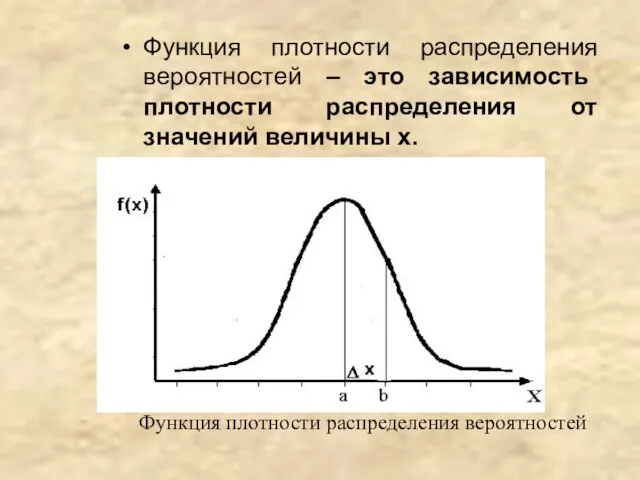
- 4. Функция плотности распределения вероятностей – это зависимость плотности распределения от значений величины x. Функция плотности распределения
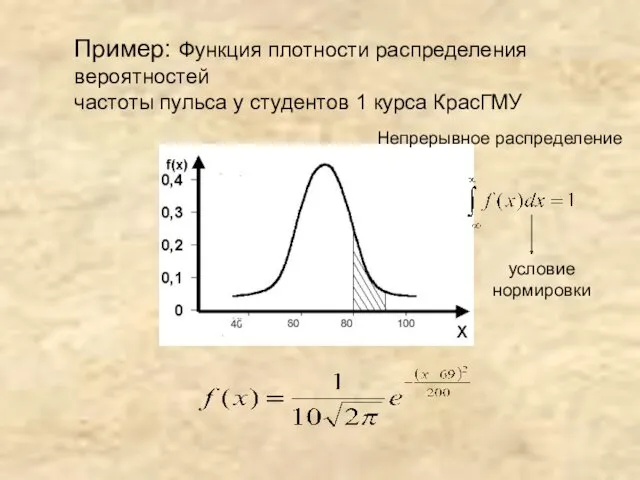
- 5. Пример: Функция плотности распределения вероятностей частоты пульса у студентов 1 курса КрасГМУ Непрерывное распределение условие нормировки
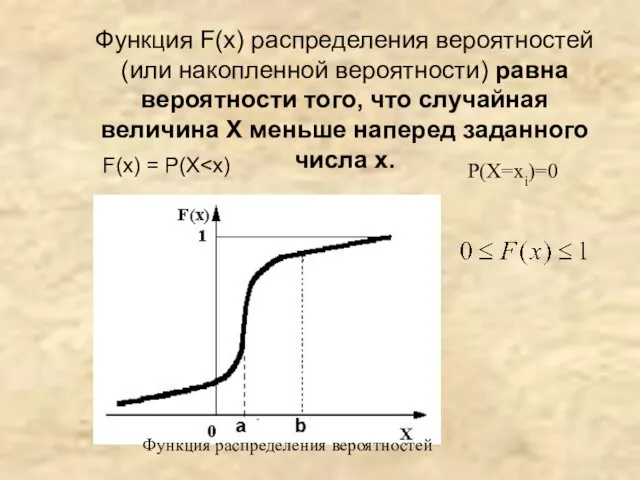
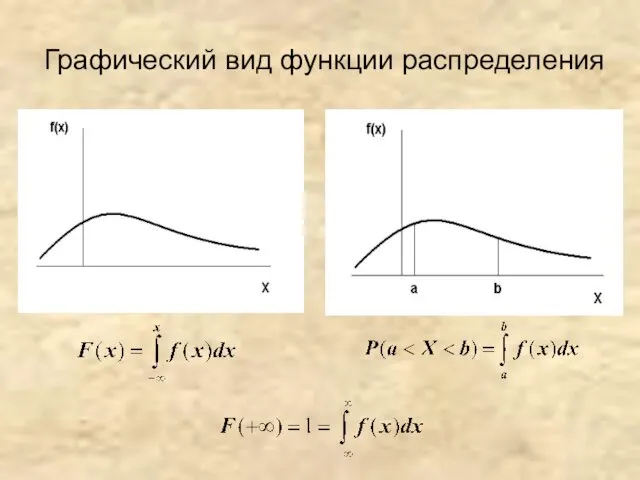
- 6. Функция F(х) распределения вероятностей (или накопленной вероятности) равна вероятности того, что случайная величина Х меньше наперед
- 7. Вероятность попадания случайной величины на заданный участок Задача: вычислить вероятность того, что случайная величина примет значение
- 8. Вероятность попадания случайной величины на заданный участок-2 По теореме сложения вероятностей получим: Вероятность попадания случайной величины
- 9. Плотность распределения случайной величины Вероятность попадания случайной величины на участок от х до х+Δх f(x) –
- 10. Графический вид функции распределения
- 11. Связь между f(x) и F(x) F(x)=Р(a f(x)=F′(x) f(x)-дифференциальная функция распределения F(x)-интегральная функция распределения F(х) – является
- 12. Задача
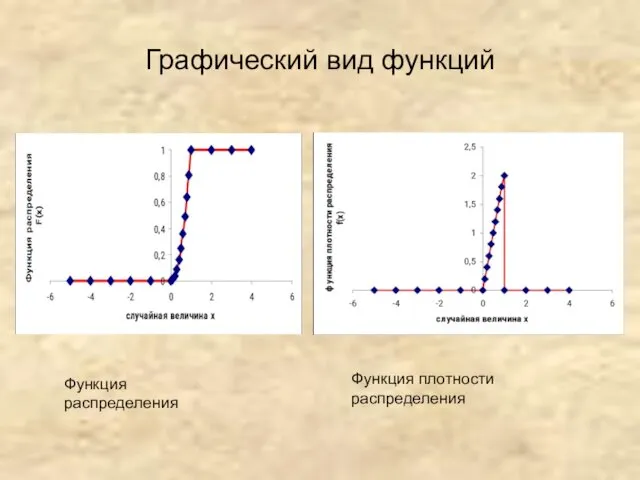
- 13. Графический вид функций Функция распределения Функция плотности распределения
- 14. Примеры: Задана функция распределения вероятностей непрерывной случайной величины: Найти: а)значение с, б)функцию плотности распределения вероятностей f(Х),
- 15. Решение: Константу С находим из условия :
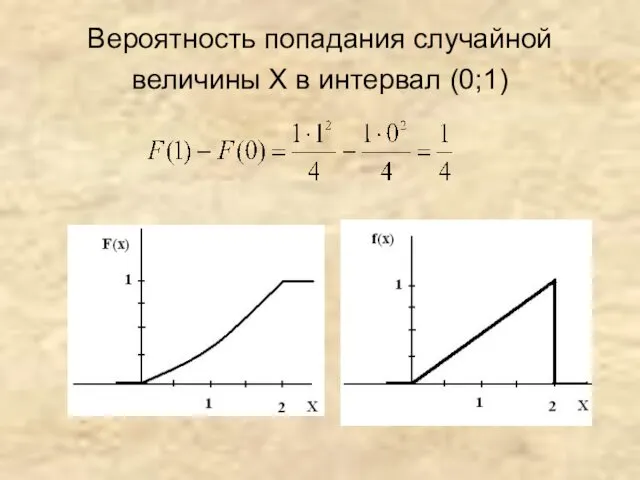
- 16. Вероятность попадания случайной величины Х в интервал (0;1)
- 17. Основные числовые характеристики непрерывных случайных величин Математическое ожидание Дисперсия Среднее квадратическое отклонение
- 19. Свойства математического ожидания Математическое ожидание постоянной величины С равно этой постоянной: М(С)=С Постоянный множитель можно выносить
- 20. Свойства дисперсии случайной величины Дисперсия постоянной величины С равна нулю: D(C)=0 Постоянный множитель можно выносить за
- 22. Скачать презентацию





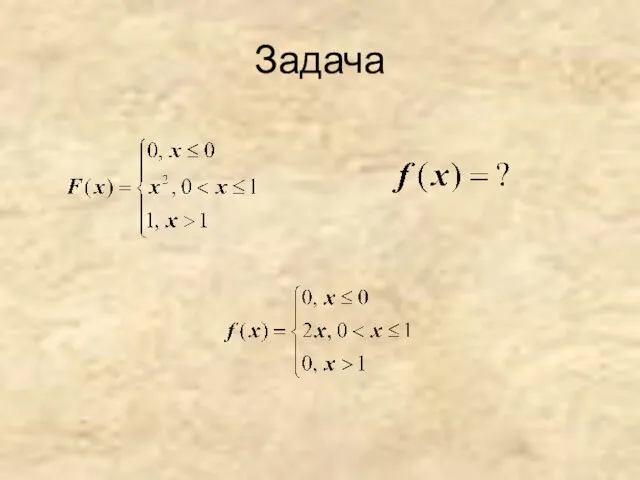



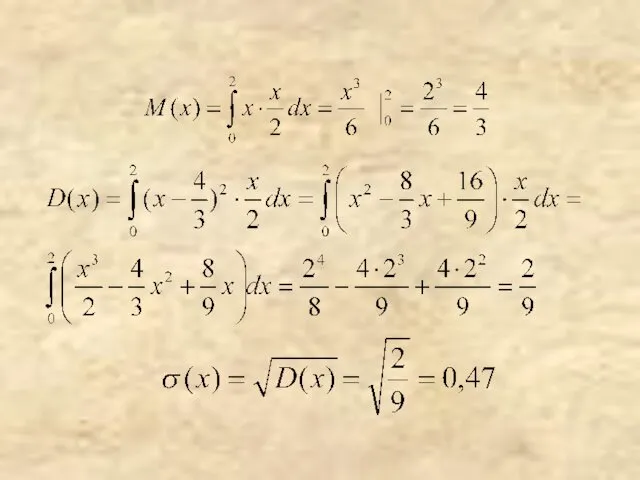


 Педагогические технологии на основе личностно-ориентированного подхода
Педагогические технологии на основе личностно-ориентированного подхода Конструкторское бюро 13.04-19.04
Конструкторское бюро 13.04-19.04 Неоплатонизм
Неоплатонизм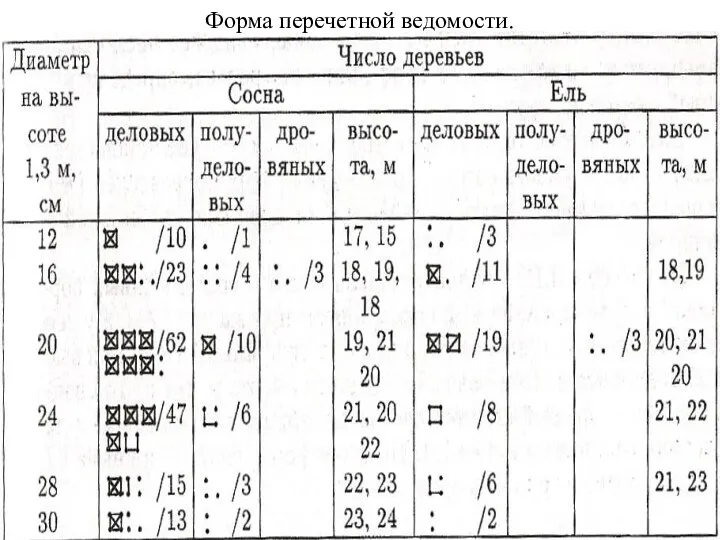 Определение запаса насаждения
Определение запаса насаждения Дефекты сварных швов
Дефекты сварных швов Организация исследовательской деятельности учащихся на уроках математики.
Организация исследовательской деятельности учащихся на уроках математики. Повышение интереса к профессии сварщик
Повышение интереса к профессии сварщик Полевой отчёт ООО Нива
Полевой отчёт ООО Нива Презентация к семинару ИКТ на уроках английского языка 1 часть
Презентация к семинару ИКТ на уроках английского языка 1 часть Этапы развития жизни на земле
Этапы развития жизни на земле Борисова К. Н. 41-АН
Борисова К. Н. 41-АН Сущность и роль коммуникаций в системе управления
Сущность и роль коммуникаций в системе управления Меню на 02.06.15 по столовой ООО ЧАША. Завтрак
Меню на 02.06.15 по столовой ООО ЧАША. Завтрак Электрические станции и подстанции. Введение. Основные понятия, термины и определения
Электрические станции и подстанции. Введение. Основные понятия, термины и определения Медико-социальное сопровождение сирот
Медико-социальное сопровождение сирот Районный семинар школьных библиотекарей
Районный семинар школьных библиотекарей Термические повреждения, ожоги, отморожения, электротравма
Термические повреждения, ожоги, отморожения, электротравма Выдающиеся женщины-художницы
Выдающиеся женщины-художницы Игры для развития мелкой моторики своими руками.
Игры для развития мелкой моторики своими руками. Православные праздники на Руси
Православные праздники на Руси Демографическая ситуация в современной России
Демографическая ситуация в современной России Презентация Обучение дошкольников правилам дорожного движения
Презентация Обучение дошкольников правилам дорожного движения Моя улица
Моя улица Ремонт КДЦ
Ремонт КДЦ Использование нетрадиционной техники изобразительной деятельности в работе с детьми дошкольного возраста
Использование нетрадиционной техники изобразительной деятельности в работе с детьми дошкольного возраста Иероним Босх (около 1460-1516гг.)
Иероним Босх (около 1460-1516гг.) Презентация Художественное выпиливание
Презентация Художественное выпиливание Подготовка к ОГЭ по алгебре (базовая часть)
Подготовка к ОГЭ по алгебре (базовая часть)