Содержание
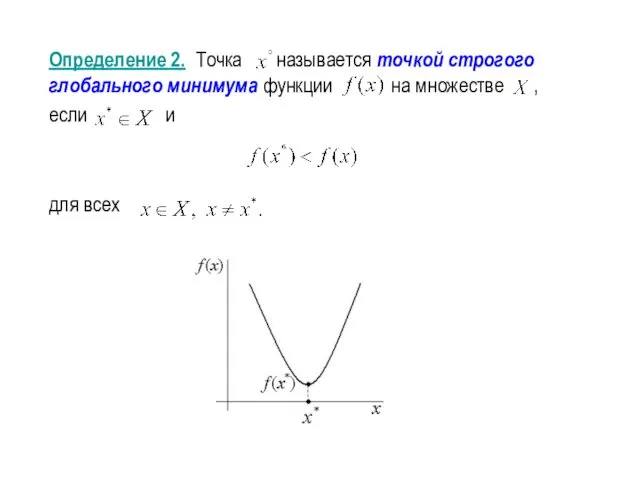
- 2. Определение 2. Точка называется точкой строгого глобального минимума функции на множестве , если и для всех
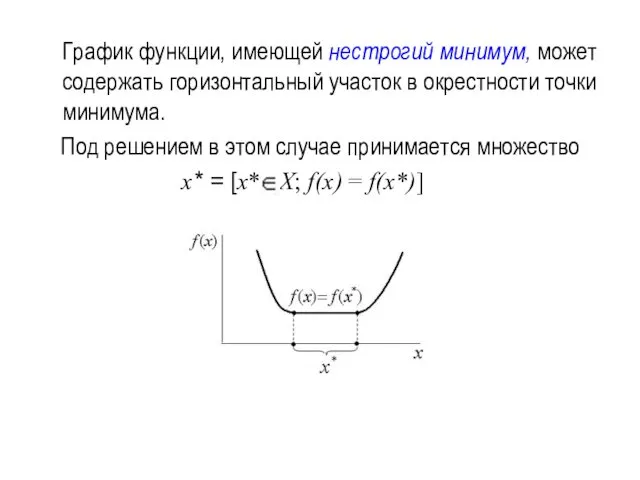
- 3. График функции, имеющей нестрогий минимум, может содержать горизонтальный участок в окрестности точки минимума. Под решением в
- 4. Определение 3. Точка называется точкой локального минимума функции , если существует такое число , что для
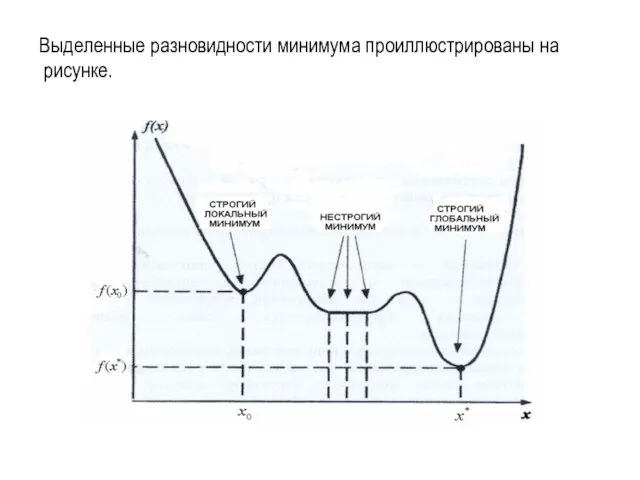
- 5. Выделенные разновидности минимума проиллюстрированы на рисунке.
- 6. в) алгоритм нахождения точки минимума с использованием производной Найти первую производную функции Найти критические (стационарные) точки
- 7. г) достаточные условия экстремума Если функция дважды непрерывно дифференцируема, то достаточным условием минимума является положительность, а
- 8. Пример 2.1. Решить пример 1.1, используя необходимые и достаточные условия экстремума. Решение. Целевая функция имеет вид
- 9. Из условия найдем: т.е. высота цилиндрического бака должна быть равна диаметру основания бака.
- 10. 2.2. Численные методы поиска экстремума функции одной переменной 2.2.1. Постановка задачи. Будем предполагать, что в пределах
- 12. Унимодальная функция может быть непрерывной, разрывной или дискретной. Для проверки унимодальной функции на практике обычно используют
- 13. Решение. Функция определена при Найдем ее производные: при Следовательно, функция унимодальна на интервале Первая производная при
- 14. 2.2.2. Стратегии поиска Существуют две принципиально различные стратегии выбора точек, в которых производится вычисление значений целевой
- 15. Последовательную стратегию можно реализовать двумя способами: построением последовательности вложенных в друг друга интервалов, каждый из которых
- 16. Алгоритм последовательной стратегии Выбор начального интервала изменения параметра , называемого интервалом неопределенности. Границы интервала выбираются таким
- 17. Прием уменьшения интервала неопределенности Пусть функция унимодальна на интервале и ее минимум достигается в точке Возьмем
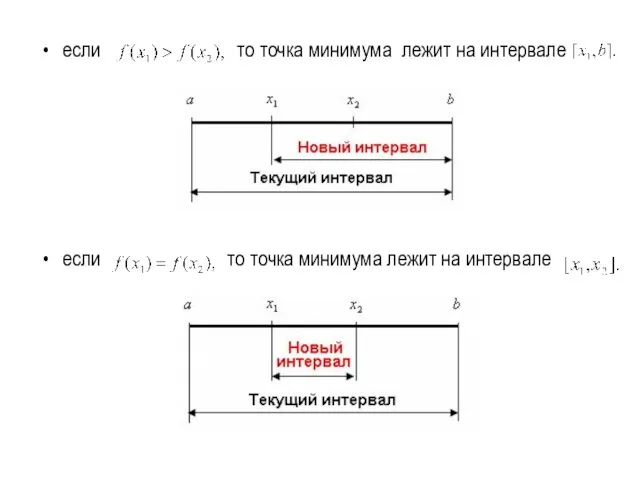
- 18. если то точка минимума лежит на интервале если то точка минимума лежит на интервале
- 19. Рассмотрим наиболее распространенные в практике следующие приближенные методы поиска минимума: метод равномерного поиска; метод дихотомии; метод
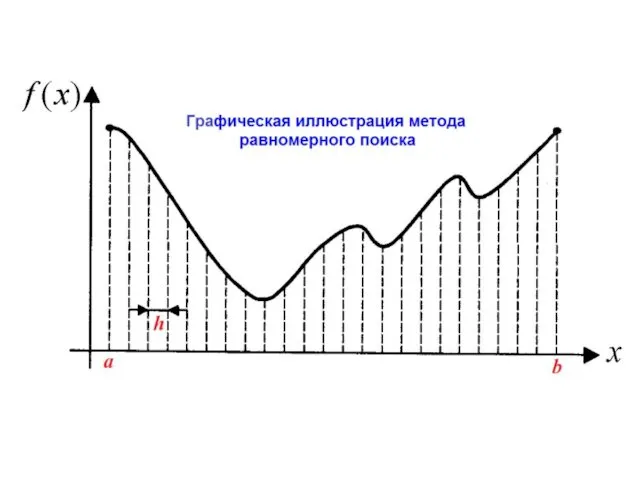
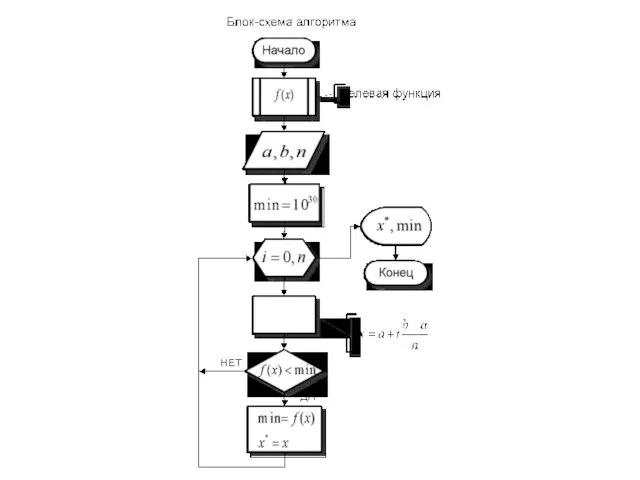
- 20. 2.2.3. Метод равномерного поиска Метод относится к пассивным стратегиям. Задается начальный интервал неопределенности и количество вычислений
- 21. Среди точек находится точка , в которой целевая функция принимает наименьшее значение Эффективность метода невелика и
- 24. 2.2.4. Метод дихотомии Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность поиска
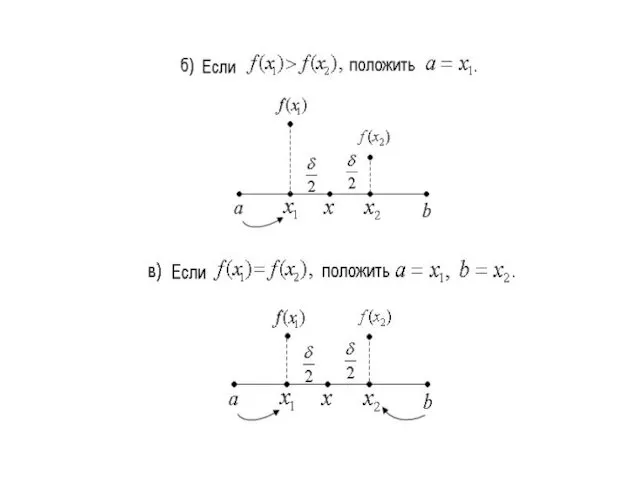
- 25. Вычисляются функции и Сравниваются полученные значения и находится новый уменьшенный интервал неопределенности:
- 27. Затем снова вычисляются координаты и и продолжается поиск. За оценку прекращения поиска принимают а за минимальное
- 28. Точность на м шаге вычислений определяется неравенством Отсюда следует, что для достижения точности потребуется итераций. На
- 30. Скачать презентацию



















 Пошаговая инструкция по заполнению заявления о выдаче повторного свидетельства о рождении
Пошаговая инструкция по заполнению заявления о выдаче повторного свидетельства о рождении Сын есімнің сөйлемдегі қызметі
Сын есімнің сөйлемдегі қызметі Маркировка кабелей
Маркировка кабелей Сигналы светофора
Сигналы светофора Jeopardy. Ad main topic here
Jeopardy. Ad main topic here опыт работы презентация
опыт работы презентация Основные положения законодательства об охране окружающей среды
Основные положения законодательства об охране окружающей среды Методика изучения и обобщения передового педагогического опыта
Методика изучения и обобщения передового педагогического опыта Английские надписи на одежде и их влияние на культуру современных подростков
Английские надписи на одежде и их влияние на культуру современных подростков Сварка чугуна
Сварка чугуна Внеклассное занятие Если добрый ты...
Внеклассное занятие Если добрый ты... Портрет выпускника начальной школы по ФГОС
Портрет выпускника начальной школы по ФГОС Духовные искания Пьера Безухова
Духовные искания Пьера Безухова Отчет о создании развивающей среды.
Отчет о создании развивающей среды. Из опыта работы учителя математики Никифоровой З.З
Из опыта работы учителя математики Никифоровой З.З Орфография. Слитное, раздельное, дефисное написание. Написание не с разными частями речи
Орфография. Слитное, раздельное, дефисное написание. Написание не с разными частями речи Динамические структуры данных
Динамические структуры данных Инструкция по проведению Вводного тренинга ЭТП
Инструкция по проведению Вводного тренинга ЭТП География черной металлургии
География черной металлургии
 Организация исследовательское деятельности в учебном процессе. Из опыта работы учителя географии
Организация исследовательское деятельности в учебном процессе. Из опыта работы учителя географии Ликвидация дефектных участков на морских нефте- и газопроводах
Ликвидация дефектных участков на морских нефте- и газопроводах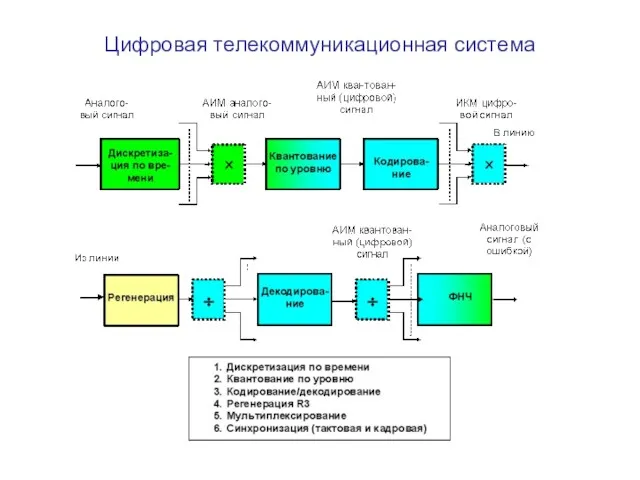 Цифровая телекоммуникационная система
Цифровая телекоммуникационная система Культура и духовная жизнь общества
Культура и духовная жизнь общества Причины и клинические синдромы перинатального поражения нервной системы в периоде новорожденности
Причины и клинические синдромы перинатального поражения нервной системы в периоде новорожденности Экологические болезни
Экологические болезни Выпускники
Выпускники Household items furniture
Household items furniture