Содержание
- 2. План лекции: Актуальность темы. Проверка простых гипотез о параметрах. Сравнение выборочной средней с гипотетической генеральной средней
- 3. Проверка простых гипотез о параметрах
- 4. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности. Алгоритм может быть использован при проверке соответствия
- 5. 1. Дисперсия генеральной совокупности известна. Генеральная средняя неизвестна, но предполагается равной а0. Пусть из нормальной генеральной
- 6. т.е. надо установить значимо или незначимо отличаются выборочная и генеральная средняя. В качестве критерия служит величина:
- 7. по таблице функции Лапласа найдем критическую точку двусторонней критической области по равенству:Ф(uкр)=(1-α)/2 Если |Uнабл| Если |Uнабл|>uкр
- 8. Пример1. Из нормальной генеральной совокупности извлечена выборка объемом n=36 и по ней найдена выборочная средняя =21,6,
- 9. 2. Дисперсия генеральной совокупности неизвестна (например, при малых выборках). В качестве критерия принимают СВ Т, которая
- 10. Если |Tнабл| Если |Tнабл|>tкрдвуст нулевую гипотезу отвергают б) Н0: а= а0 Н1: а> а0 По таблице
- 11. Пример: По выборке объема n=20, извлеченной из нормальной генеральной совокупности, найдена выборочная средняя =16 и исправленное
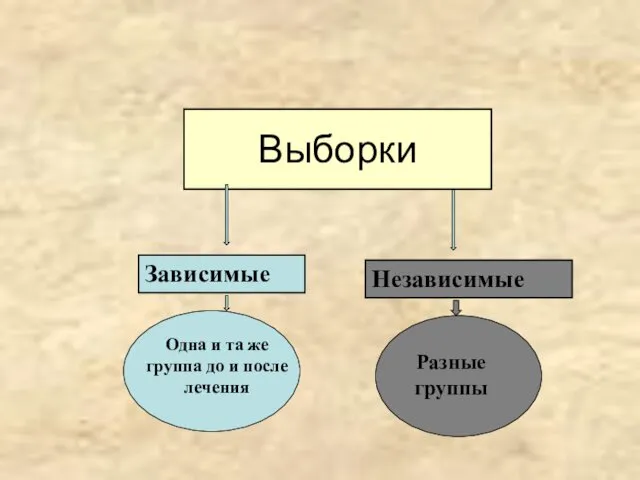
- 12. Выборки Зависимые Независимые Одна и та же группа до и после лечения Разные группы
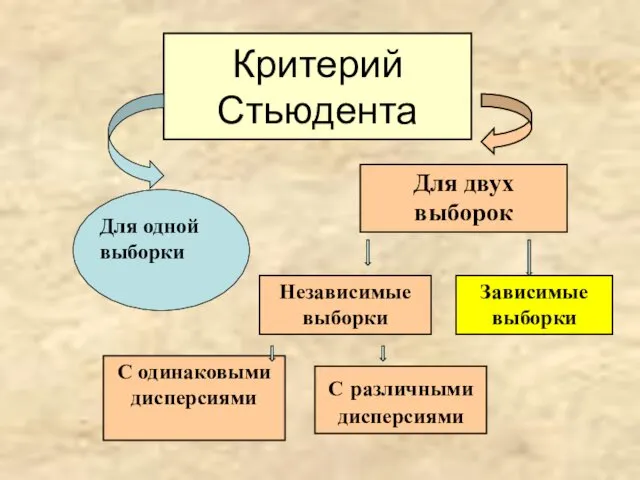
- 13. Критерий Стьюдента Для одной выборки Для двух выборок Независимые выборки Зависимые выборки С одинаковыми дисперсиями С
- 14. Критерий tнабл для определения достоверности средней арифметической одной выборки tнабл tнабл> tкр (df, α=0,05) выборка не
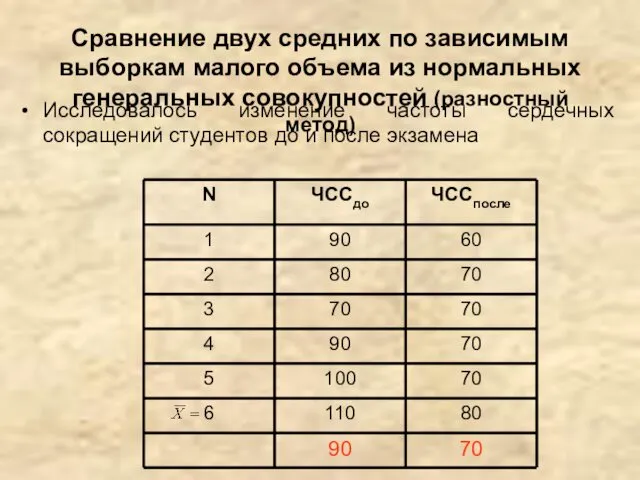
- 15. Сравнение двух средних по зависимым выборкам малого объема из нормальных генеральных совокупностей (разностный метод) Исследовалось изменение
- 16. 1. Найдем среднее арифметическое значение выборки: 2. Вычислим дисперсию (рассеивание ряда) где df = n-1 число
- 17. 3. Среднее квадратическое отклонение выборки: Это - точечные (т.е. выраженные одним значением) параметры малой выборки. Результат
- 18. 4. Определим среднюю квадратическую ошибку: 5. Определим доверительный интервал для генеральной средней. По таблицам Стьюдента находим
- 19. Для второго ряда измерений:
- 20. Нулевая гипотеза: В генеральной совокупности нет различия между средними арифметическими выборок Проверяем гипотезу по критерию Стьюдента
- 21. Нулевая гипотеза: Определяем критическое значение критерия Стьюдента (tкр)для α=0,05 и df=n-1 Если tнабл ≥ tкр нулевая
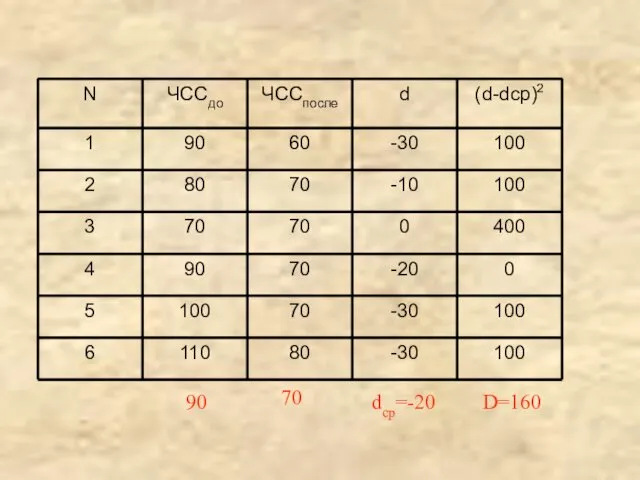
- 22. dср=-20 90 70 D=160
- 23. Для разности:
- 24. Определим, достоверно ли определена средняя арифметическая разности: tкр(0,05;5)=2,57 tнабл> tкр Это означает, что нулевая гипотеза отвергается,
- 25. Примечание:*-значимость различий α Рассчитаем эффект: ЧСС студентов после экзамена снизилась на 22% (α
- 26. Сравнение генеральных средних двух групп по независимым выборкам из нормальных совокупностей. Допущения: В генеральной совокупности выборки
- 27. Нормированное отклонение: 1. Для n≥30, ошибка разницы sd определяется по формуле: Пример: n1=40 n2=50 Определить значимость
- 28. 2. Для n tнабл= =0,277 tкрит (0,05)=1,96, tнабл Разница средних арифметических недостоверна.
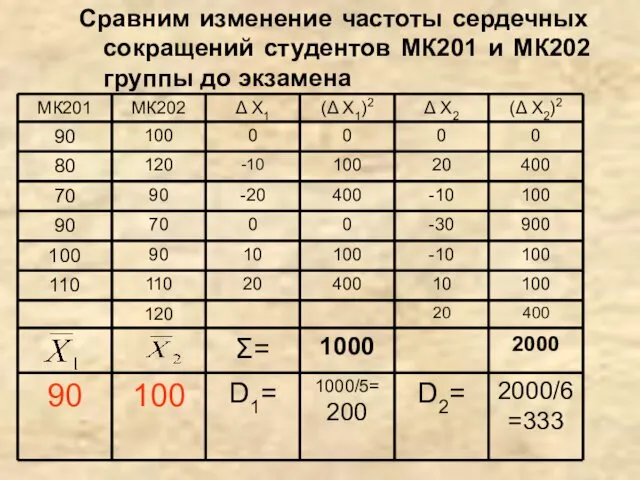
- 29. Сравним изменение частоты сердечных сокращений студентов МК201 и МК202 группы до экзамена
- 30. df=(n1-1)+(n2-1)=11 tкр=2,2 tнабл Fкрит(6,5,0,05)=4,95 1,67
- 32. Сводка основных формул Средняя арифметическая выборки Дисперсия Среднее квадратическое отклонение Средняя квадратическая ошибка:
- 33. Критерий нормированного отклонения (по Стьюденту) Доверительный интервал для генеральной средней Критерий tнабл для определения достоверности средней
- 34. Критерий tэксп разности средних арифметических двух выборок а) n≥30 б) n
- 35. Заключение Нами рассмотрены критерии проверки однородности средних по выборкам из нормальных совокупностей.
- 36. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Попов А.М. Теория вероятней и математическая статистика /А.М. Попов, В.Н. Сотников. –
- 38. Скачать презентацию

















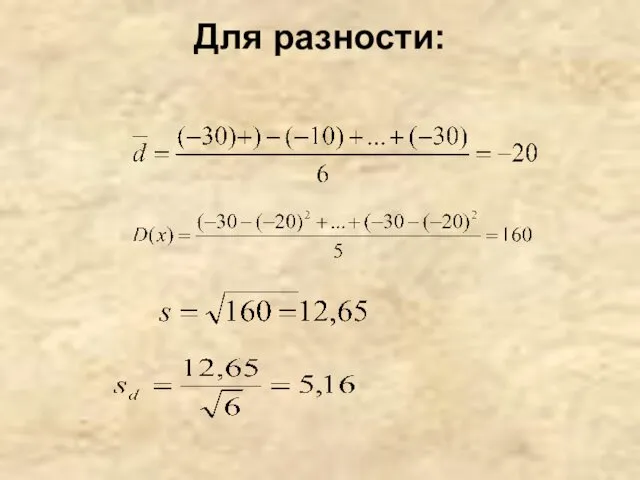












 Зубченко Раїса Федорівна
Зубченко Раїса Федорівна Игрушка из зубочисток, 4 класс
Игрушка из зубочисток, 4 класс Функции мышления. Классификация мышления. Объект и субъект мышления
Функции мышления. Классификация мышления. Объект и субъект мышления Электрические машины. Лекция 4
Электрические машины. Лекция 4 Портфолио воспитателя
Портфолио воспитателя Кейс-метод при обучении химии в условиях перехода на ФГОС ООО
Кейс-метод при обучении химии в условиях перехода на ФГОС ООО Учим стихи.
Учим стихи. Опухоли легких у детей
Опухоли легких у детей Введение в патологическую анатомию, история патологической анатомии. Альтерация. Некроз, апоптоз
Введение в патологическую анатомию, история патологической анатомии. Альтерация. Некроз, апоптоз Газобаллонное оборудование четвертого поколения
Газобаллонное оборудование четвертого поколения РобоПлатформа. Старт 2.0 Урок 10
РобоПлатформа. Старт 2.0 Урок 10 Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Рецепты гениальных сценариев
Рецепты гениальных сценариев 12 апреля — День Космонавтики
12 апреля — День Космонавтики Developing of telecommunications
Developing of telecommunications Физиологические механизмы боли
Физиологические механизмы боли Деление и умножение натуральных чисел
Деление и умножение натуральных чисел Маркетинговая информация и выбор исследования
Маркетинговая информация и выбор исследования презентация
презентация Профилактика онкологических заболеваний в России
Профилактика онкологических заболеваний в России Е.Пермяк Самое страшное. 4 класс
Е.Пермяк Самое страшное. 4 класс Равнины
Равнины Футуризм в искусстве
Футуризм в искусстве 20240125_prezentatsiya_1
20240125_prezentatsiya_1 Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Мета-информация на странице
Мета-информация на странице МЕТОДИЧЕСКАЯ РАЗРАБОТКА РАЗДЕЛА ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ОРИГАМИ БАЗОВЫЕ ФОРМЫ
МЕТОДИЧЕСКАЯ РАЗРАБОТКА РАЗДЕЛА ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ОРИГАМИ БАЗОВЫЕ ФОРМЫ Сельское хозяйство, его отраслевая структура
Сельское хозяйство, его отраслевая структура