Слайд 2Резистор R в цепи синусоидального тока

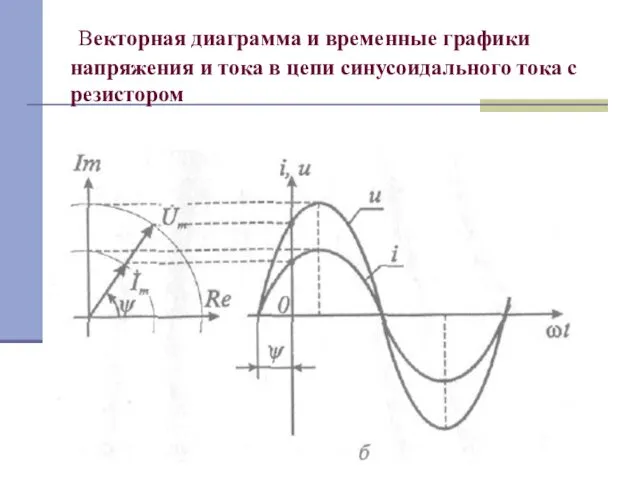
Слайд 3 Векторная диаграмма и временные графики напряжения и тока в цепи синусоидального тока
с резистором
Слайд 4Комплексное сопротивление и комплексная проводимость цепи с резистором
Комплексное сопротивление z и комплексная проводимость
Y цепи с резистором являются вещественными величинами и равны соответственно его активному сопротивлению R и активной проводимости g, а разность фаз φ = 0; векторы Um и Iт совпадают по направлению.

Слайд 5 Катушка индуктивности в цепи синусоидального тока

Слайд 6Векторная диаграмма и временные графики напряжения и тока в цепи с катушкой индуктивности
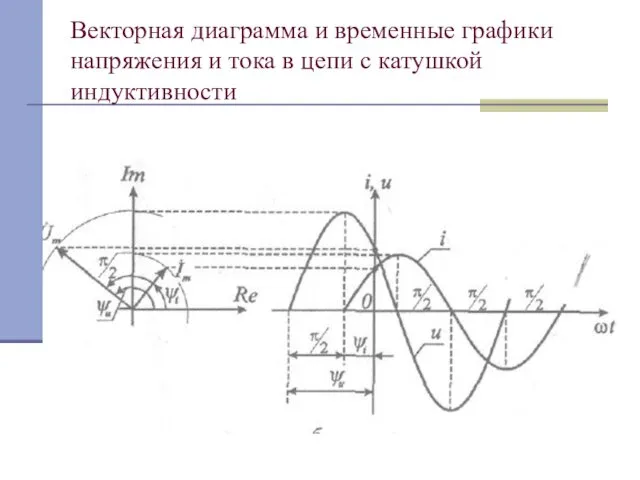
Слайд 7Графики индуктивных сопротивления и проводимости
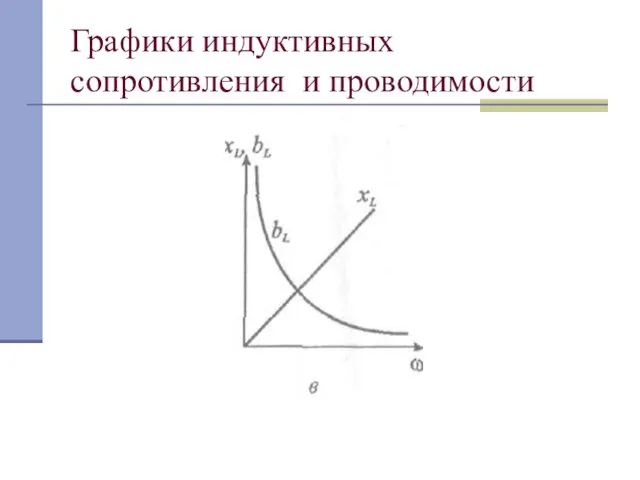
Слайд 8Комплексное сопротивление катушки индуктивности
Xl = ωL –индуктивное сопротивление, имеющее размерность в Омах
[Ом].
![Комплексное сопротивление катушки индуктивности Xl = ωL –индуктивное сопротивление, имеющее размерность в Омах [Ом].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65808/slide-7.jpg)
Слайд 9Физический смысл индуктивного сопротивления
Физический смысл индуктивного сопротивления — противодействие прохождению тока за счет
ЭДС самоиндукции eL, возникающей в катушке индуктивности при прохождении по ней переменного тока и направленной навстречу приложенному к ней напряжению.

Слайд 10Комплексная проводимость индуктивного сопротивления

Слайд 11Конденсатор в цепи синусоидального тока

Слайд 12Конденсатор в цепи синусоидального тока
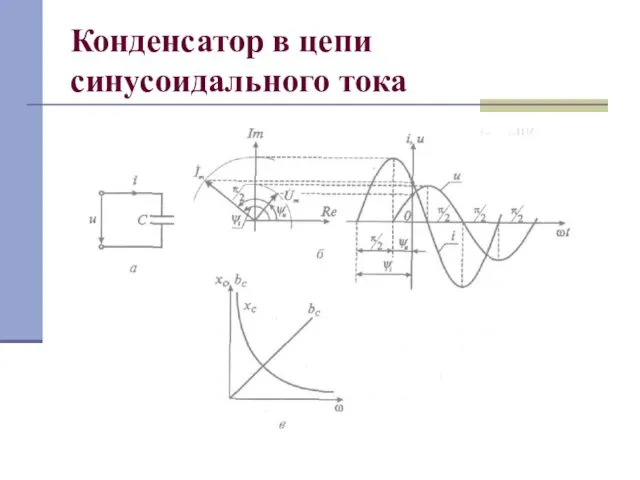
Слайд 13Конденсатор в цепи синусоидального тока
φ = –π/2, т. е. ток через конденсатор опережает
приложенное к нему напряжение по фазе π/2

Слайд 14Комплексное сопротивление конденсатора
хс = 1/ωС - емкостное сопротивление, измеряемое в Омах [Ом].
Физический
смысл емкостного сопротивления — противодействие напряжению той разностью потенциалов, которая возникает при заряде конденсатора.
![Комплексное сопротивление конденсатора хс = 1/ωС - емкостное сопротивление, измеряемое в Омах [Ом].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65808/slide-13.jpg)
Слайд 15Комплексная проводимость конденсатора
где bс = ωС- емкостная проводимость.
При ω = 0
она равна нулю, т. е. на постоянном токе ветвь с конденсатором равносильна разрыву ветви.

Слайд 16Цепь синусоидального напряжения с последовательным соединением R, L, С
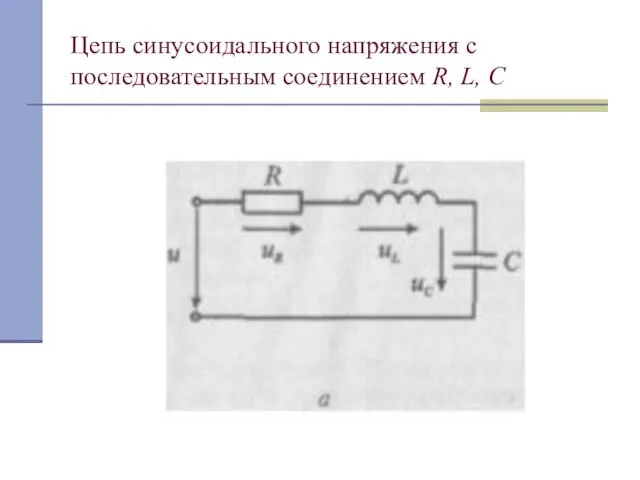
Слайд 17Цепь синусоидального тока с последовательным соединением R, L u C

Слайд 18Комплексное сопротивление цепи с последовательным соединением R, L u C

Слайд 19Векторная диаграмма цепи с последовательным соединением R, L, С
при φ>0
xl > хс;
φ > 0, ток в цепи отстает от приложенного к ней напряжения.
Цепь носит индуктивный характер.

Слайд 20Векторная диаграмма цепи с последовательным соединением R, L, С для φ<0
xl < хс;
φ > 0, ток опережает напряжение .
Цепь
носит емкостный характер.

Слайд 21Векторная диаграмма цепи с последовательным соединением R, L, С для φ=0
xl = хс;
φ=0, ток совпадает с напряжением.
Цепь носит характер активного сопротивления.

Слайд 23Понятие о настройке и расстройке контура
На частотах ω < ω0 полное сопротивление последовательного
колебательного контура носит емкостный характер, а на частотах ω > ω0 — индуктивный.
Когда частота сигнала совпадает с резонансной частотой ω0 , то контур настроен на частоту сигнала.
Когда ω ≠ ω0 контур расстроен; расстройка контура тем сильнее, чем больше его реактивное сопротивление х, и равна нулю, если х = 0.

Слайд 24Волновое или характеристическое сопротивление контура
Сопротивление индуктивности или емкости контура при резонансе называется волновым
или характеристическим сопротивлением контура.

Слайд 25Резонанс напряжений
Напряжения на реактивных элементах контура при резонансе равны по амплитуде и обратны
по фазе.

Слайд 26Добротность контура
Добротность контура определяет эффективность или качество контура и в радиотехнических контурах достигает
значения Q = 200—500.
Величина, обратная Q, - затухание контура.

Слайд 27Затухание контура
Величина, обратная Q, называется затуханием контура.

Слайд 28Применение последовательного колебательного контура
Последовательный колебательный контур широко применяется в различных электро -
и радиотехнических схемах и устройствах главным образом в качестве резонансной системы, т. е. системы, «усиливающей» в Q раз гармонические колебания, поступающие на ее вход.

Слайд 29Энергия при резонансе напряжений
При резонансе суммарная энергия, запасенная в контуре, остается неизменной: происходит
лишь непрерывное периодическое перераспределение (колебание) энергии, запасенной в индуктивности и емкости.
В момент, когда энергия магнитного поля катушки индуктивности достигает максимума, энергия электрического поля конденсатора равна нулю, и наоборот; происходит обмен энергии между индуктивностью L и емкостью С.

Слайд 30Параллельный колебательный контур
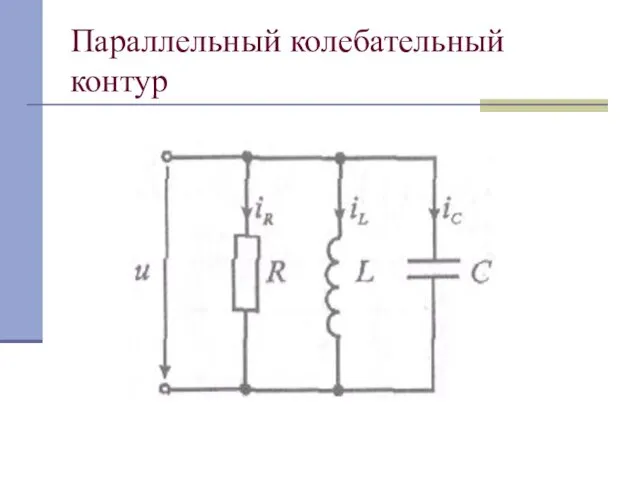
Слайд 31Параллельный колебательный контур







![Комплексное сопротивление катушки индуктивности Xl = ωL –индуктивное сопротивление, имеющее размерность в Омах [Ом].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65808/slide-7.jpg)





![Комплексное сопротивление конденсатора хс = 1/ωС - емкостное сопротивление, измеряемое в Омах [Ом].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/65808/slide-13.jpg)

















 Эстетическое воспитание дошкольников через декоративно – прикладное искусство.
Эстетическое воспитание дошкольников через декоративно – прикладное искусство. Самостоятельная работа студента
Самостоятельная работа студента Государства Востока: традиционное общество в эпоху раннего Нового времени
Государства Востока: традиционное общество в эпоху раннего Нового времени Проект Моя профессия - педагог
Проект Моя профессия - педагог турнир по рус.языку
турнир по рус.языку Воспитание культуры речи с использование игровых технологий
Воспитание культуры речи с использование игровых технологий Решение задач с помощью рациональных уравнений
Решение задач с помощью рациональных уравнений Музеї другої половини XIX століття
Музеї другої половини XIX століття Стратегическое z планирование
Стратегическое z планирование Внутренняя среда организма. Значение крови и ее состав
Внутренняя среда организма. Значение крови и ее состав 35 лет
35 лет Графические возможности Turbo Pascal
Графические возможности Turbo Pascal Презентация Развитие речи детей дошкольного возраста.
Презентация Развитие речи детей дошкольного возраста. Учитесь властвовать собой - не попадая в плен зависимостей и привычек!
Учитесь властвовать собой - не попадая в плен зависимостей и привычек! Eschyo_odna_RKh
Eschyo_odna_RKh Слайд-фильм по охране труда
Слайд-фильм по охране труда Влияние инфляции на семейную экономику
Влияние инфляции на семейную экономику Банковская система
Банковская система Путешествие по России
Путешествие по России Famous People of Great Britain
Famous People of Great Britain Презентация открытого урока Классификация растений и их размещение в природных комплексах
Презентация открытого урока Классификация растений и их размещение в природных комплексах Окончание смутного времени в России. Воцарение династии Романовых
Окончание смутного времени в России. Воцарение династии Романовых Морские котики г. Северодвинск. Квест-игра Неразлучники
Морские котики г. Северодвинск. Квест-игра Неразлучники Розіборка ноутбука Lenovo G580
Розіборка ноутбука Lenovo G580 Бортовые системы контроля и индикации работы авиадвигателей
Бортовые системы контроля и индикации работы авиадвигателей Презентация ФГОС НОО: направленность и основа.
Презентация ФГОС НОО: направленность и основа. Виды транспорта
Виды транспорта Синтаксис. Повторение
Синтаксис. Повторение