Содержание
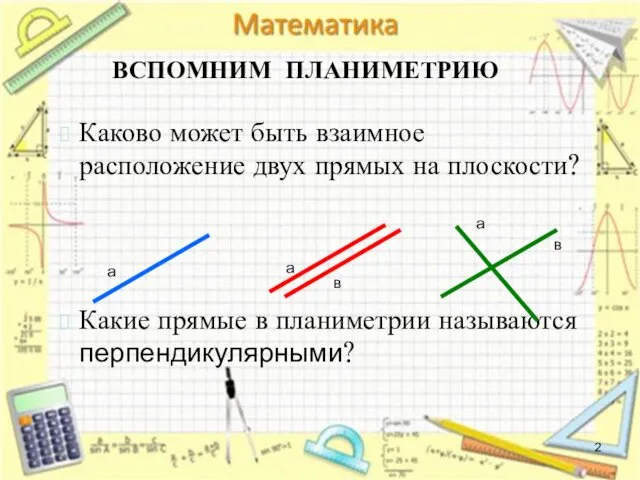
- 2. ВСПОМНИМ ПЛАНИМЕТРИЮ Каково может быть взаимное расположение двух прямых на плоскости? Какие прямые в планиметрии называются
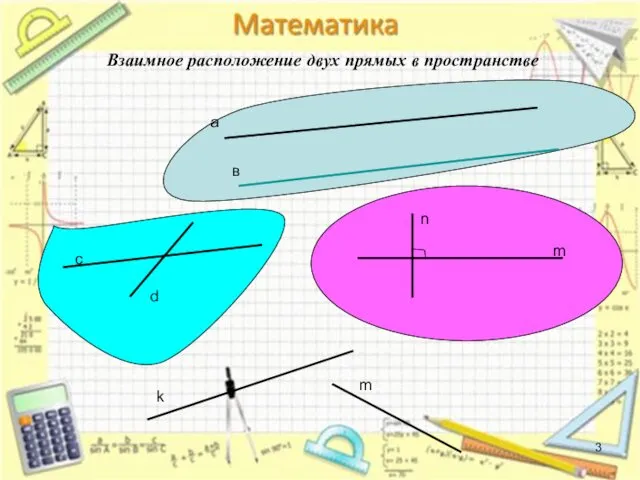
- 3. Взаимное расположение двух прямых в пространстве а в с d m n k m
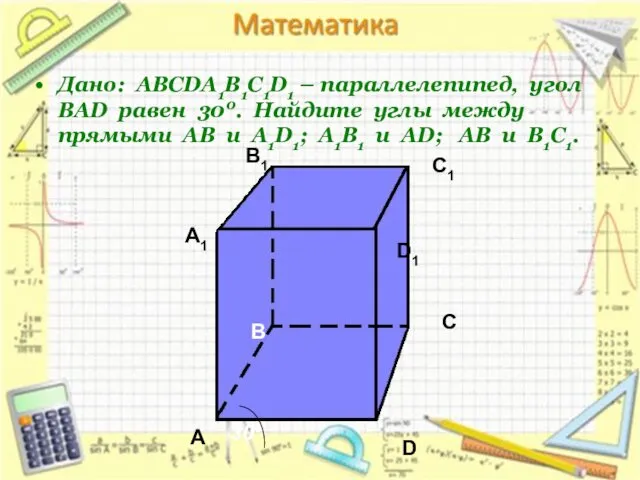
- 4. Дано: АВСDA1B1C1D1 – параллелепипед, угол ВАD равен 300. Найдите углы между прямыми АВ и А1D1; А1В1
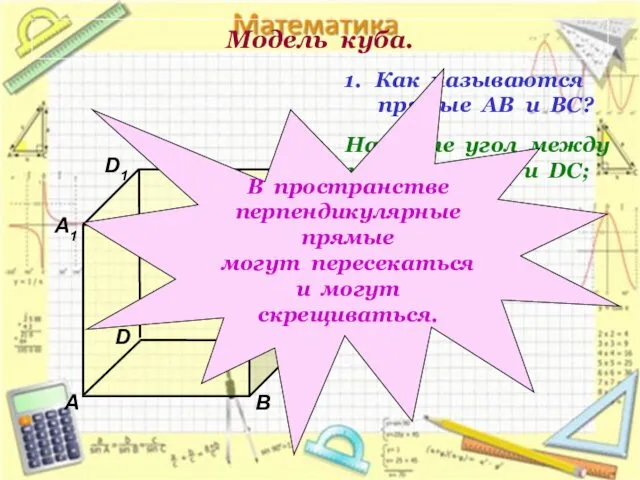
- 5. Модель куба. D1 В А1 А D С1 С В1 Как называются прямые АВ и ВС?
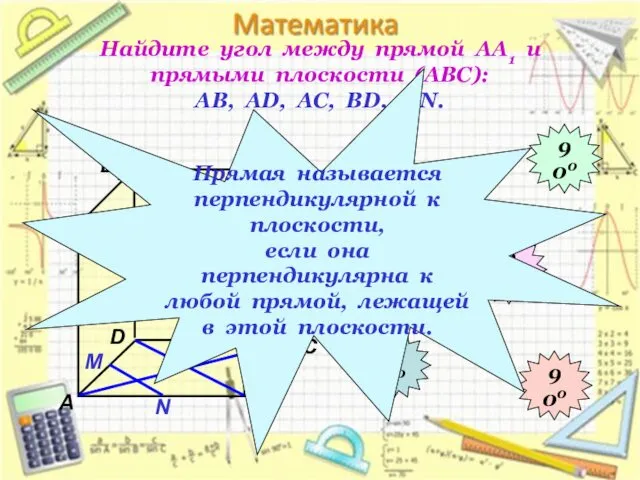
- 6. Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними
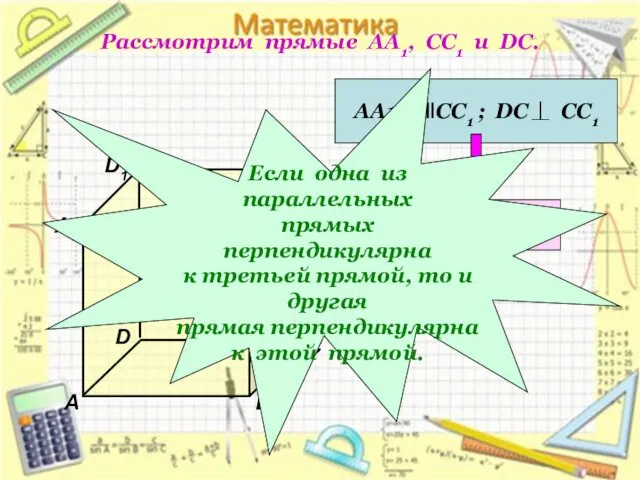
- 7. Рассмотрим прямые АА1, СС1 и DC. D1 В А1 А D С1 С В1 АА1
- 8. Свойства : 1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой прямой.
- 9. Свойства : 4. Если две различные плоскости перпендикулярны одной и той же прямой, то эти плоскости
- 10. Найдите угол между прямой АА1 и прямыми плоскости (АВС): АВ, АD, АС, ВD, МN. D1 В
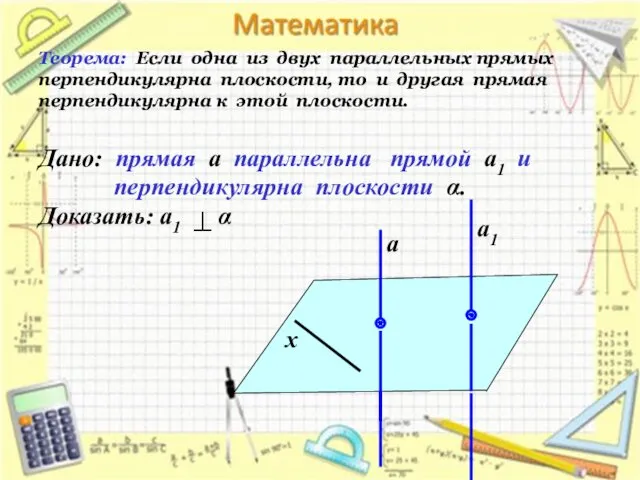
- 11. Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой
- 12. Проведем прямую х в плоскости α. Так как а⊥α, то а⊥х. По лемме о перпендикулярности двух
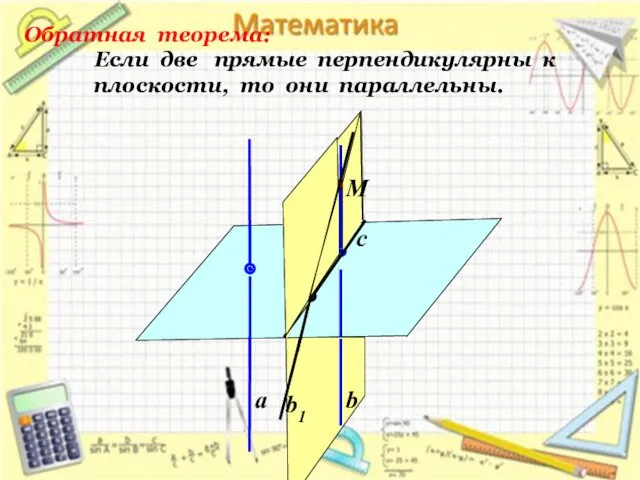
- 13. а b b1 Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны. M c
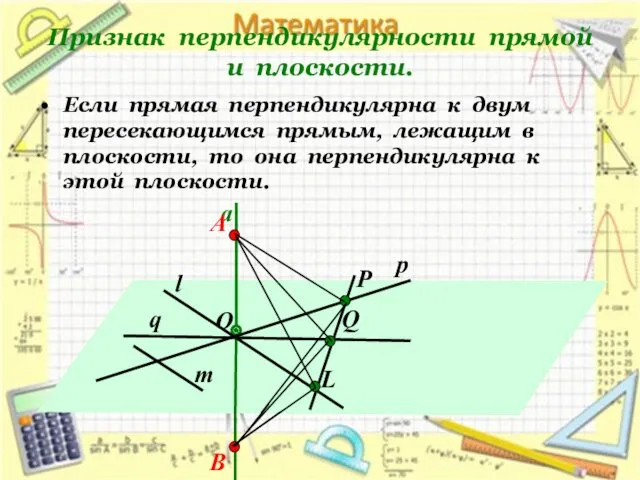
- 14. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то
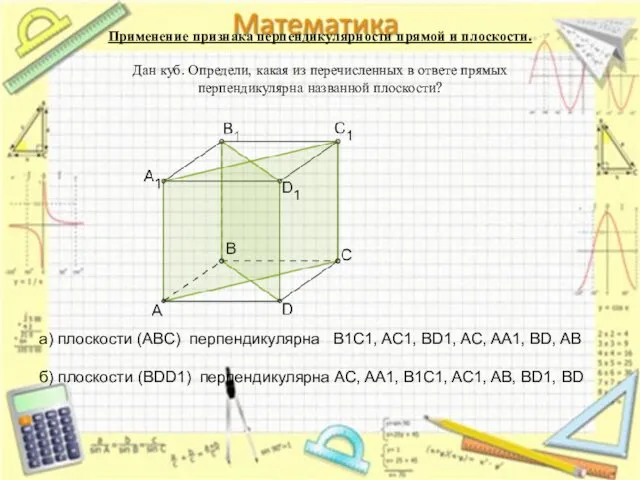
- 15. Применение признака перпендикулярности прямой и плоскости. Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна
- 17. Скачать презентацию




 История информационных войн (лекция № 2)
История информационных войн (лекция № 2) Поняття, ознаки, принципи формування сучасних міжнародних організацій
Поняття, ознаки, принципи формування сучасних міжнародних організацій Влияние оболочек Земли на формирование плодородия почв
Влияние оболочек Земли на формирование плодородия почв Невербальные средства коммуникации
Невербальные средства коммуникации Управление в биотехнических системах
Управление в биотехнических системах Уникальный тур по Центральной России. В гостях у сказки на Ласточке!
Уникальный тур по Центральной России. В гостях у сказки на Ласточке! Team Roles “Coming together is a beginning. Keeping together is progress. Working together is success” Henry Ford
Team Roles “Coming together is a beginning. Keeping together is progress. Working together is success” Henry Ford Международный проект. Бизнес-академия OriBinar
Международный проект. Бизнес-академия OriBinar 20230912_pamyat_o_holokoste_put_k_tolerantnosti
20230912_pamyat_o_holokoste_put_k_tolerantnosti Презинтация
Презинтация 21 политика
21 политика Итоги 2 триместра, 5 класс
Итоги 2 триместра, 5 класс Признаки подобия. Обобщающий урок
Признаки подобия. Обобщающий урок Круглые числа
Круглые числа Капитилизация тәсілі
Капитилизация тәсілі 70-летию Великой Победы посвящается
70-летию Великой Победы посвящается Lukoil company
Lukoil company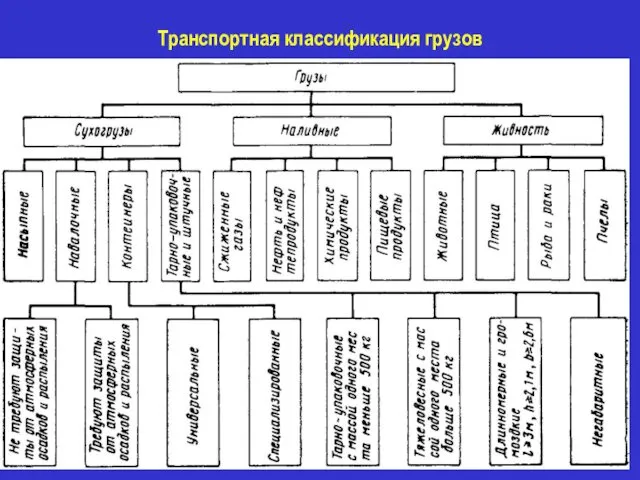 Транспортная классификация грузов
Транспортная классификация грузов Этика и право.Мастерская радости.Внеклассное мероприятие.ч.2.Сопровождение к Мини-презентациии
Этика и право.Мастерская радости.Внеклассное мероприятие.ч.2.Сопровождение к Мини-презентациии Татьянин день - День студента
Татьянин день - День студента Мировая экономика
Мировая экономика Презентация Альбина Ахатова
Презентация Альбина Ахатова Урок Ислам и наука 4-5 класс.
Урок Ислам и наука 4-5 класс. Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей
Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей Металлорежущие станки
Металлорежущие станки Le subjonctif présent. Французкий язык
Le subjonctif présent. Французкий язык Опросник описания поведения Томаса
Опросник описания поведения Томаса Строительные башенные краны
Строительные башенные краны