Содержание
- 2. Геометрические условия: ν = –1/2 (или 0, или +1/2); – уравнение Фурье. или 0 ≤ x
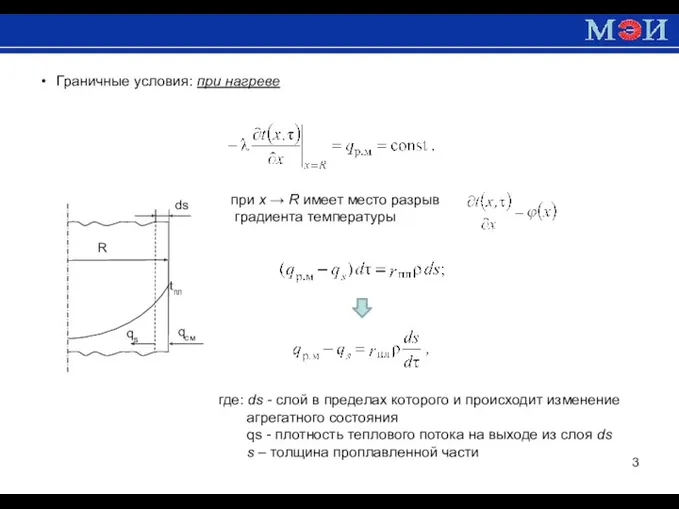
- 3. Граничные условия: при нагреве при x → R имеет место разрыв градиента температуры где: ds -
- 4. Постулата мгновенного регулярного режима (МРР) : Где: – средняя температура слоя ds; – средняя температура нерасплавленной
- 5. Подставив (2) и (3) в (1) получим: Заметим, что = ϕ(R) = ϕ(R0∙ω), где ω =
- 6. Введение Постулата мгновенного регулярного режима (МРР) : (6) Используя Cусл, получим: т.к. (7) Средняя температура слоя
- 7. Используя полученную зависимость , найдем:
- 8. Из рисунка видно, что при N ≤ 0,3 зависимость ω(F0) линейная и имеет вид: Продолжительность плавления:
- 9. О Для слоя расплава: ; -1/2 0 1/2 R0ω ≤ x ≤ R0 , ; где:
- 10. О Для нерасплавленной части тела : = -1/2, или 0, или + ½ ; При τ
- 11. Эта задача может быть решена методом МРР. Асимптотическое приближение этого решения (при N ≤ 0,3) имеет
- 13. Скачать презентацию









 Предмет, цели и задачи товароведения
Предмет, цели и задачи товароведения Визуальная диагностика нефро- и уролитиаза
Визуальная диагностика нефро- и уролитиаза Электроснабжение. Понятие о системах электроснабжения
Электроснабжение. Понятие о системах электроснабжения проектная деятельность в начальной школе
проектная деятельность в начальной школе Формирование здорового образа жизни младших школьников на уроках и во внеурочное время
Формирование здорового образа жизни младших школьников на уроках и во внеурочное время Западная Европа в V – X вв
Западная Европа в V – X вв Наблюдение за горящей свечей
Наблюдение за горящей свечей Издержки производства
Издержки производства Презентация о Сергие Радонежском
Презентация о Сергие Радонежском Презентация к уроку технологии Грибы
Презентация к уроку технологии Грибы Древний мир истории Казахстана. Каменный период
Древний мир истории Казахстана. Каменный период Презентация к классному часу Наш герой! Презентация предназначена для учащихся начальных классов, способствующая расширению кругозора и общему развитию детей. Человек и космос. Ю.А.Гагарин.
Презентация к классному часу Наш герой! Презентация предназначена для учащихся начальных классов, способствующая расширению кругозора и общему развитию детей. Человек и космос. Ю.А.Гагарин. 20230816_prezentatsiya_istoriya_raketostroeniya
20230816_prezentatsiya_istoriya_raketostroeniya Персональный компьютер
Персональный компьютер Диагностика детей по программ дополнительного образования художественно-эстетической направленности
Диагностика детей по программ дополнительного образования художественно-эстетической направленности Обобщение по теме Гидросфера
Обобщение по теме Гидросфера Книги, которые я выбираю
Книги, которые я выбираю Музыкальные формы
Музыкальные формы Парад на Красной площади 7 ноября 1941 года
Парад на Красной площади 7 ноября 1941 года Дедушка
Дедушка Образ героя Отечества в портретной живописи
Образ героя Отечества в портретной живописи Жалған круп
Жалған круп Francja
Francja Prezentatsia_Vitaliy
Prezentatsia_Vitaliy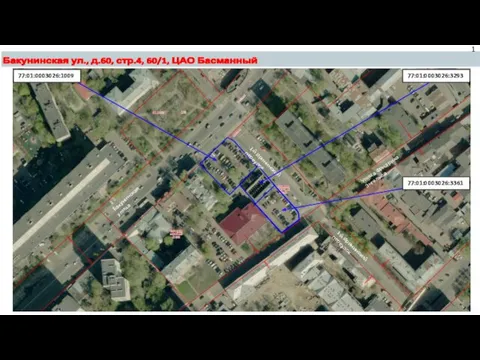 Генеральный план. Бакунинская ул.,д. 60, стр 4, 60/1, ЦАО Бесманный
Генеральный план. Бакунинская ул.,д. 60, стр 4, 60/1, ЦАО Бесманный Жұқпалы аурулардың эпидемиологиялық жіктелуі
Жұқпалы аурулардың эпидемиологиялық жіктелуі Водный транспорт. Морской и речной транспорт
Водный транспорт. Морской и речной транспорт Технология конструкционных материалов в машиностроении
Технология конструкционных материалов в машиностроении