Содержание
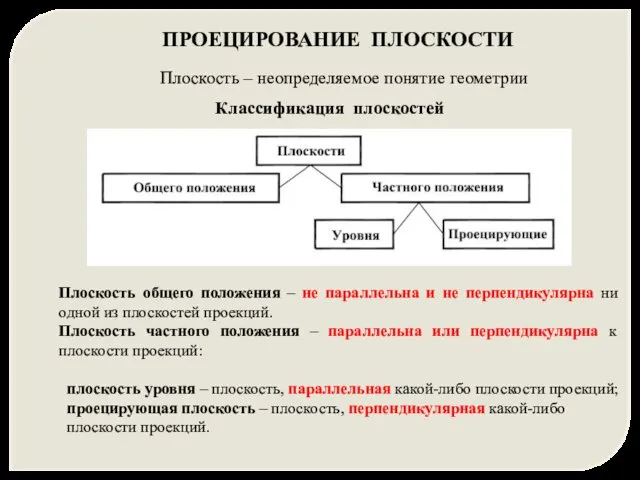
- 2. ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ Плоскость – неопределяемое понятие геометрии Плоскость общего положения – не параллельна и не перпендикулярна
- 3. Задание плоскости на чертеже Три точки, не лежащие на одной прямой, задают плоскость в пространстве ПЛОСКОСТЬ
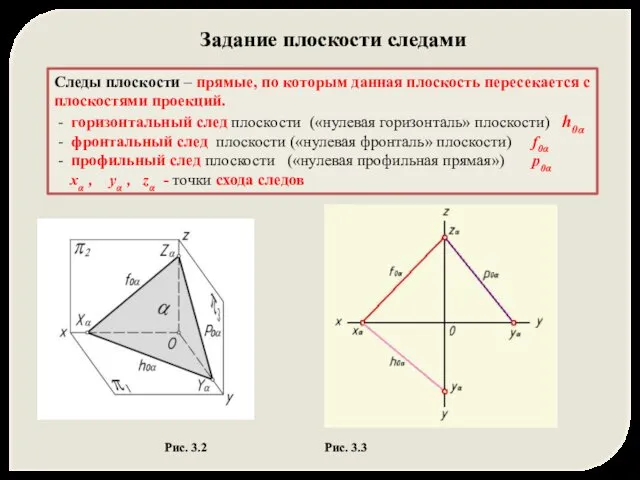
- 4. Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями проекций. - горизонтальный след плоскости
- 5. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ Признаки принадлежности: Теорема. Если точка принадлежит плоскости, то проекции точки принадлежат
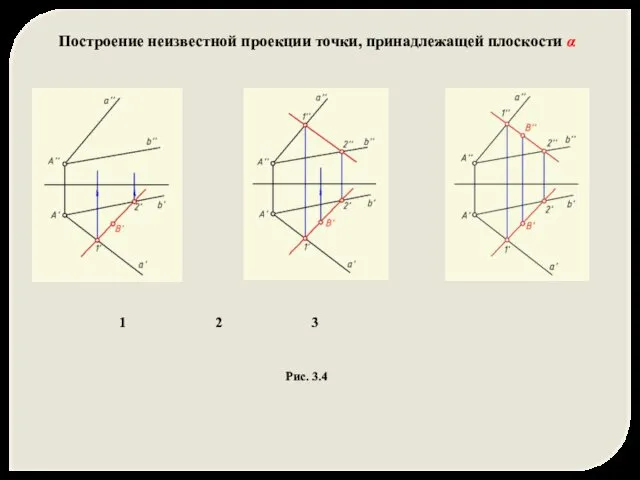
- 6. Построение неизвестной проекции точки, принадлежащей плоскости α 1 2 3 Рис. 3.4
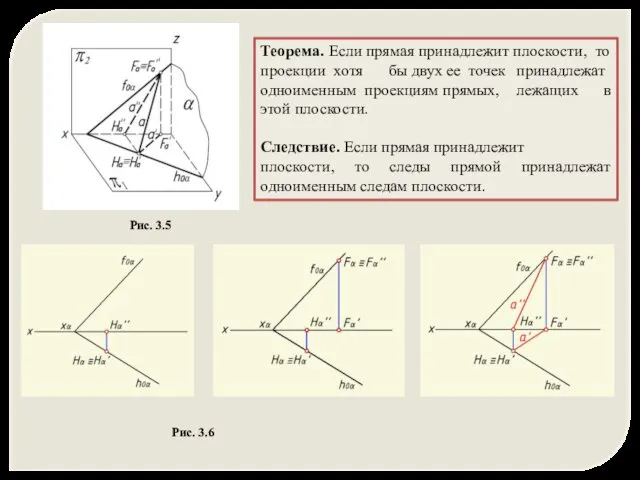
- 7. Теорема. Если прямая принадлежит плоскости, то проекции хотя бы двух ее точек принадлежат одноименным проекциям прямых,
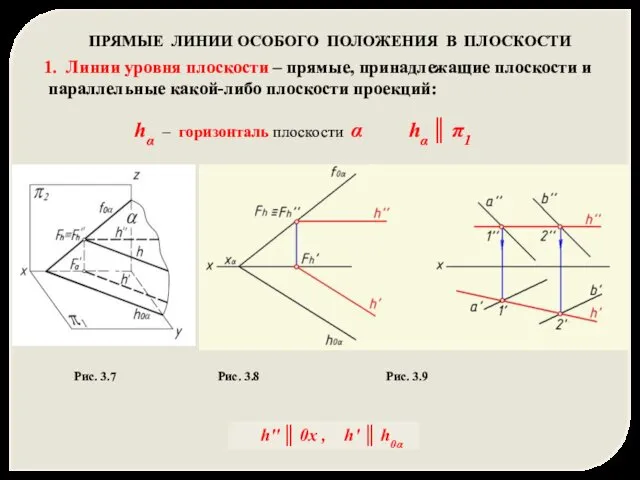
- 8. ПРЯМЫЕ ЛИНИИ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ 1. Линии уровня плоскости – прямые, принадлежащие плоскости и параллельные
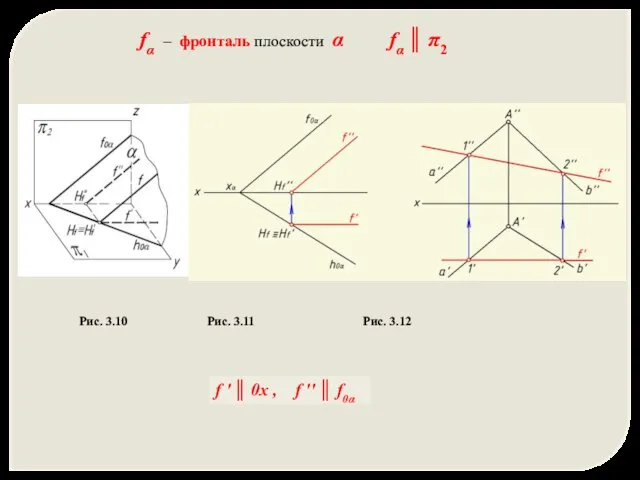
- 9. fα – фронталь плоскости α fα ║ π2 Рис. 3.10 Рис. 3.11 Рис. 3.12 f '
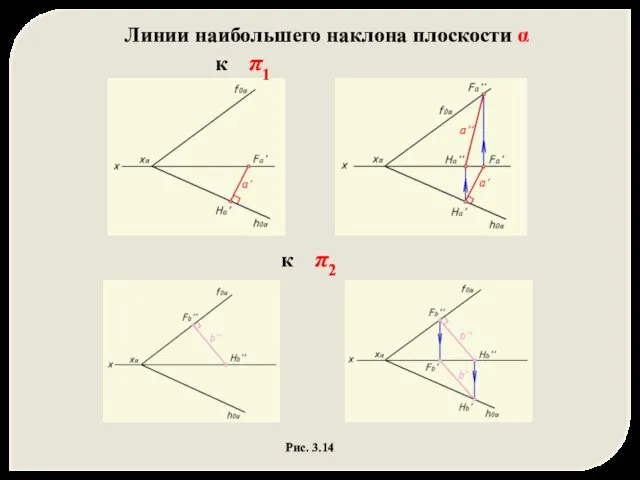
- 10. Линии наибольшего наклона (ЛНН) плоскости к плоскостям проекций – прямые, принадлежащие плоскости и образующие с соответствующей
- 11. Рис. 3.14 Линии наибольшего наклона плоскости α к π1 к π2
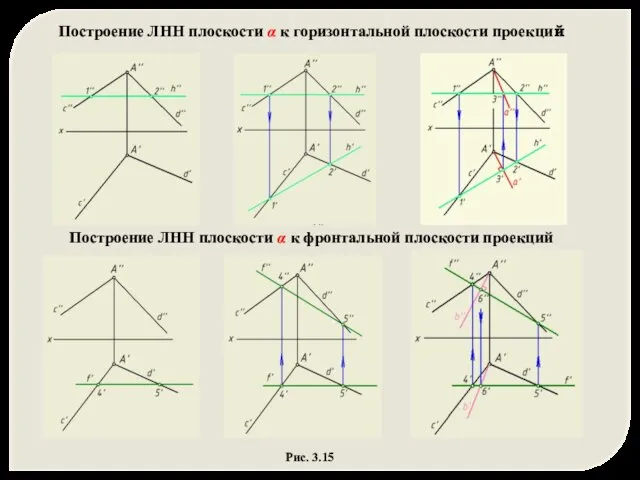
- 12. Рис. 3.15 Построение ЛНН плоскости α к фронтальной плоскости проекций Построение ЛНН плоскости α к горизонтальной
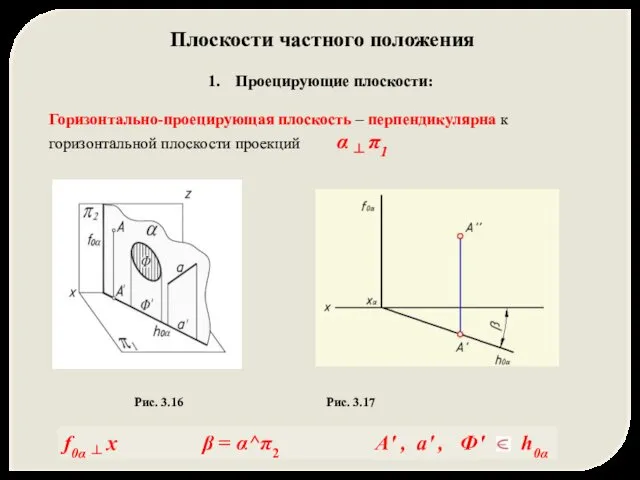
- 13. Плоскости частного положения Проецирующие плоскости: Горизонтально-проецирующая плоскость – перпендикулярна к горизонтальной плоскости проекций α ┴ π1
- 14. Фронтально-проецирующая плоскость – перпендикулярна к фронтальной плоскости проекций α ┴ π2 Рис. 3.18 Рис. 3.19 h0α
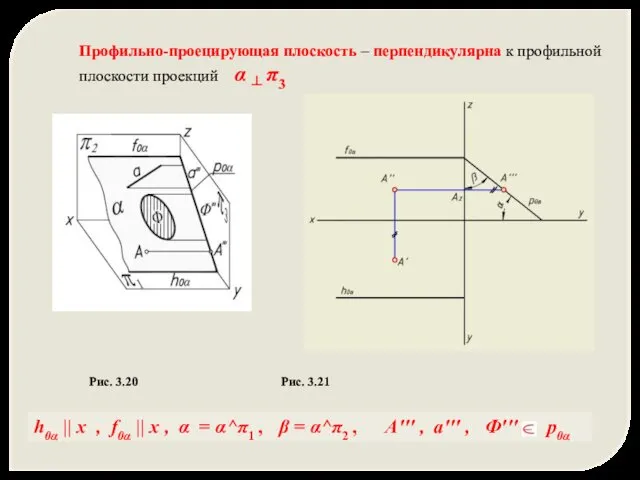
- 15. Профильно-проецирующая плоскость – перпендикулярна к профильной плоскости проекций α ┴ π3 Рис. 3.20 Рис. 3.21 h0α
- 16. 2. Плоскости уровня: Горизонтальная плоскость – параллельна горизонтальной плоскости проекций α ║ π1 Плоскости частного положения
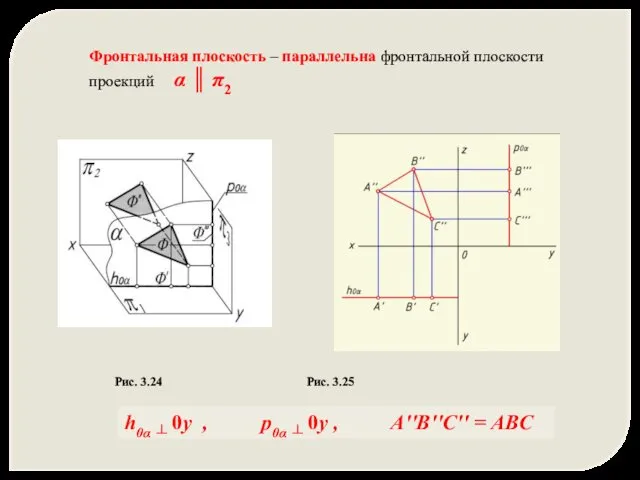
- 17. Фронтальная плоскость – параллельна фронтальной плоскости проекций α ║ π2 Рис. 3.24 Рис. 3.25 h0α ┴
- 18. Профильная плоскость – параллельна профильной плоскости проекций α ║ π3 Рис. 3.26 Рис. 3.27 h0α ┴
- 19. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 20. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая параллельна плоскости, то проекции данной прямой параллельны одноименным проекциям
- 21. ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Две плоскости параллельны, если проекции двух пересекающихся прямых одной плоскости параллельны одноименным
- 22. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая перпендикулярна плоскости, то горизонтальная проекция прямой перпендикулярна горизонтальной проекции
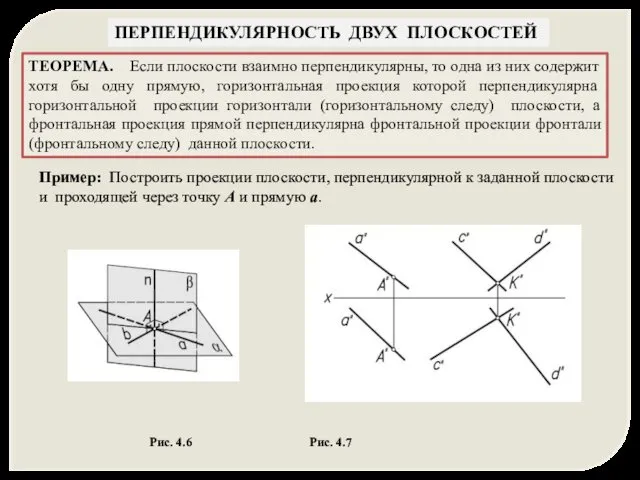
- 23. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Если плоскости взаимно перпендикулярны, то одна из них содержит хотя бы одну
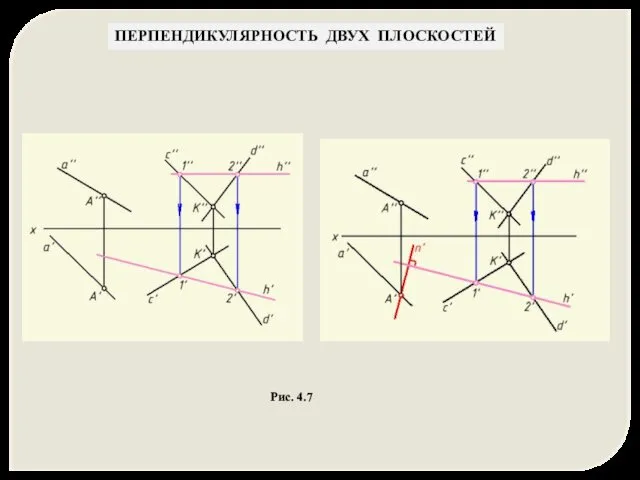
- 24. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Рис. 4.7
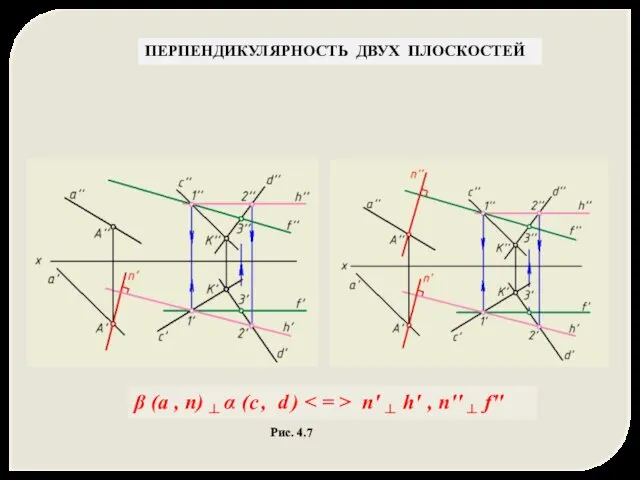
- 25. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Рис. 4.7 β (а , n) ┴ α (c , d ) n'
- 26. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Пример: Построить проекции плоскости, перпендикулярной к заданной плоскости и проходящей через точку A
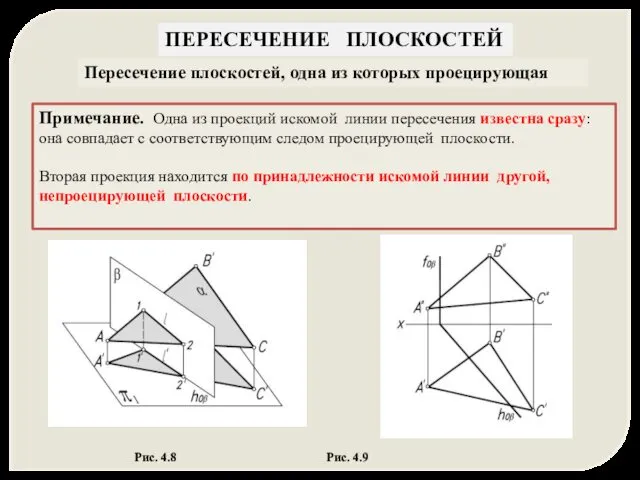
- 27. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ Пересечение плоскостей, одна из которых проецирующая Примечание. Одна из проекций искомой линии пересечения известна
- 28. Пересечение плоскостей, одна из которых проецирующая Рис. 4.9 β ∩ α (α ┴ π1) = >
- 29. Пересечение двух плоскостей общего положения Алгоритм решения: Ввести плоскость-посредник γ1 (γ1 ┴ π) Построить линии пересечения
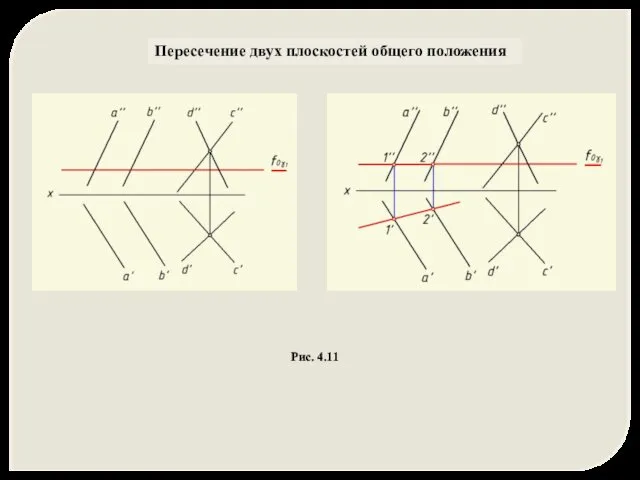
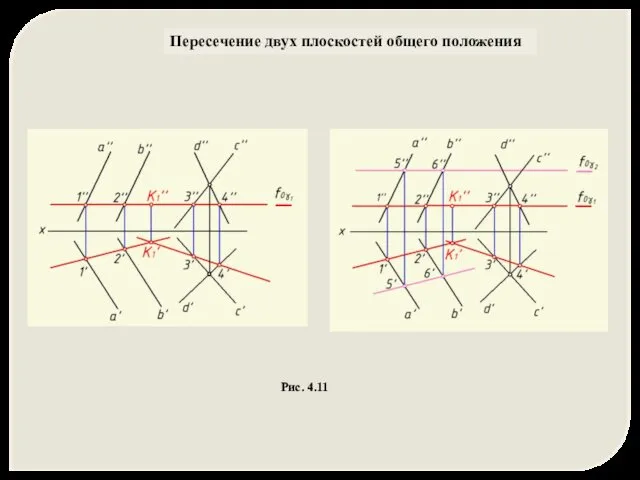
- 30. Пересечение двух плоскостей общего положения Рис. 4.11
- 31. Пересечение двух плоскостей общего положения Рис. 4.11
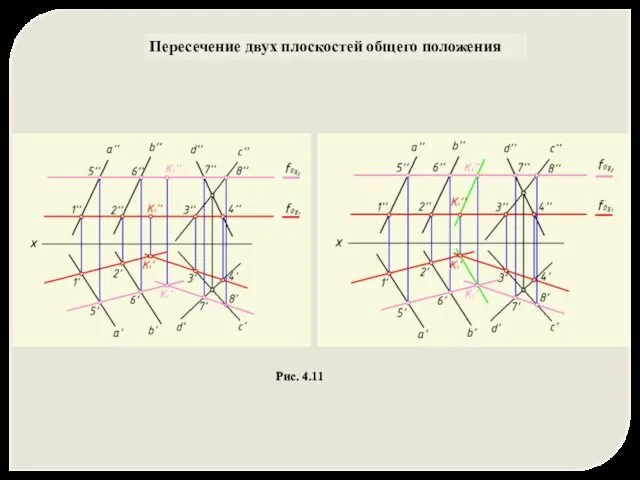
- 32. Рис. 4.11 Пересечение двух плоскостей общего положения
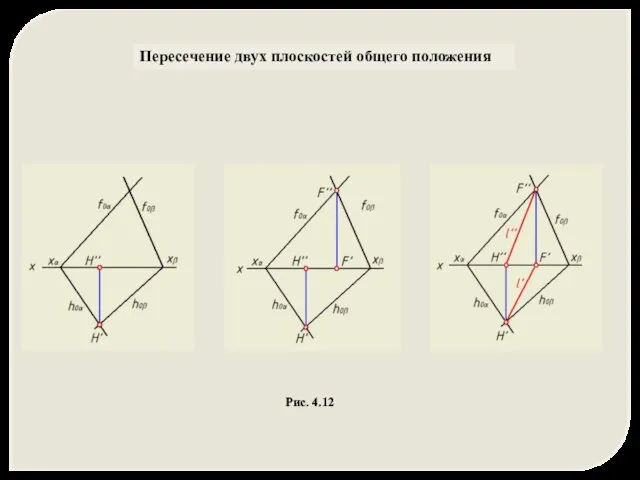
- 33. Пересечение двух плоскостей общего положения Рис. 4.12
- 34. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ 1. Пересечение прямой общего положения с проецирующей плоскостью Одна из поверхностей –
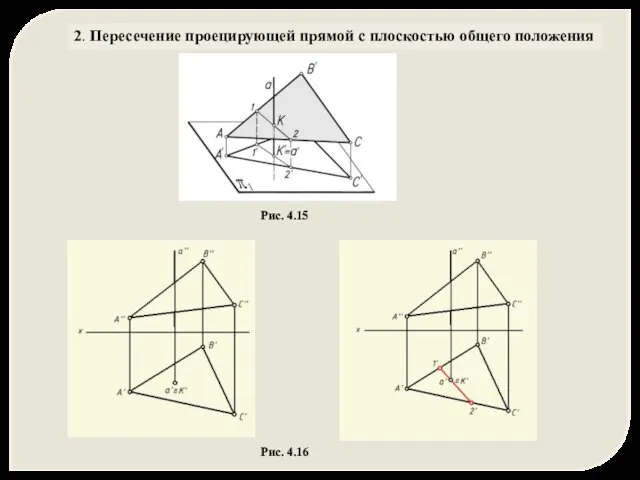
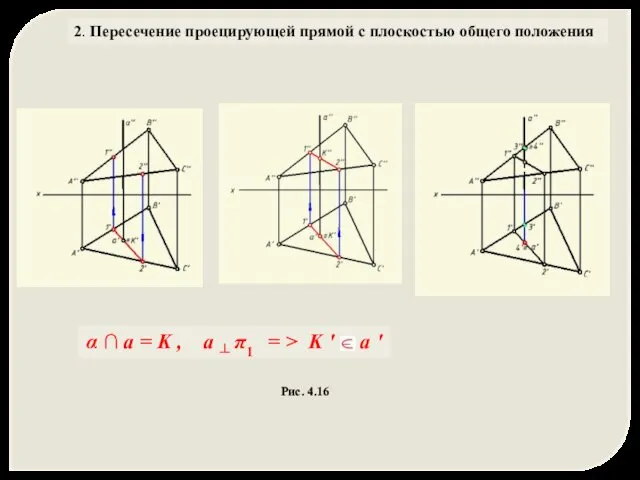
- 35. 2. Пересечение проецирующей прямой с плоскостью общего положения Рис. 4.15 Рис. 4.16
- 36. 2. Пересечение проецирующей прямой с плоскостью общего положения Рис. 4.16 α ∩ а = K ,
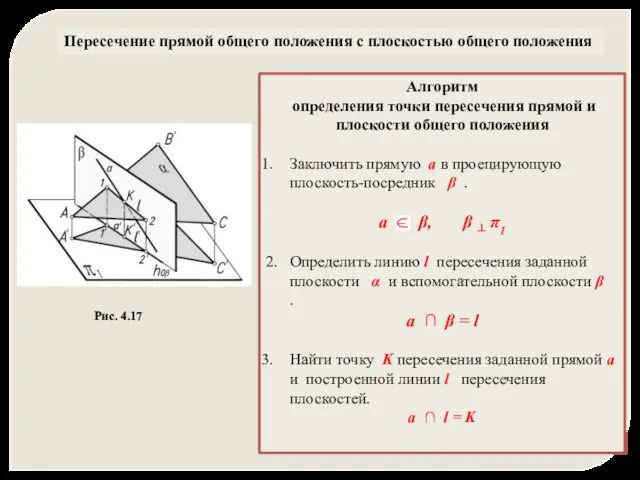
- 37. Пересечение прямой общего положения с плоскостью общего положения Алгоритм определения точки пересечения прямой и плоскости общего
- 38. Задача. Построить проекции точки пересечения прямой а с плоскостью, заданной пересекающимися прямыми b и c .
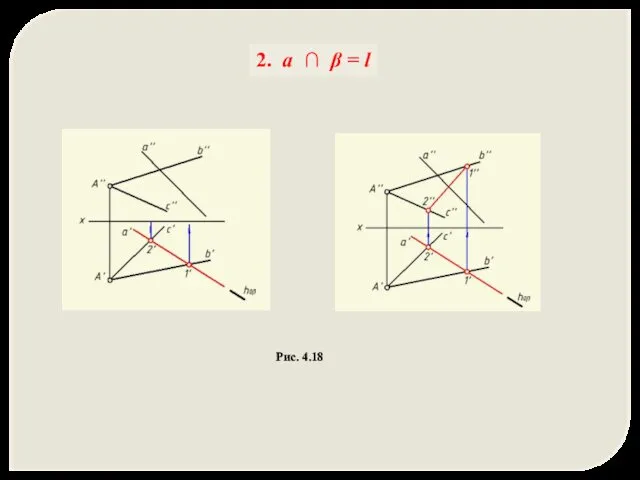
- 39. 2. a ∩ β = l Рис. 4.18
- 41. Скачать презентацию















 Кислородсодержащие органические вещества
Кислородсодержащие органические вещества Создание теста через программу MyTest
Создание теста через программу MyTest Физические свойства Металлов
Физические свойства Металлов Организация помощи при автодорожной травме. Осмотр
Организация помощи при автодорожной травме. Осмотр Стресс в профессиональной деятельности: причины и методы преодоления
Стресс в профессиональной деятельности: причины и методы преодоления С днем рождения
С днем рождения Изготовление домашнего халата
Изготовление домашнего халата Деление обыкновенных дробей
Деление обыкновенных дробей Егіз ұрықпен босанушы әйелдерде босанғаннан кейін қан кетудің алдын алу
Егіз ұрықпен босанушы әйелдерде босанғаннан кейін қан кетудің алдын алу ВКР: Цифровий термометр на мікроконтролері PIC16f628a
ВКР: Цифровий термометр на мікроконтролері PIC16f628a Зимующие птицы
Зимующие птицы Родительское собрание О подростковом возрасте
Родительское собрание О подростковом возрасте жизнь возле свалки
жизнь возле свалки История троллейбуса БТЗ-5276-04
История троллейбуса БТЗ-5276-04 Litania do Dzieciątka Jezus
Litania do Dzieciątka Jezus Фруктовое пиво - новый тренд? Что нам с этим делать?
Фруктовое пиво - новый тренд? Что нам с этим делать? Синдром раздраженного кишечника
Синдром раздраженного кишечника Гипотоническая болезнь. Коллапс
Гипотоническая болезнь. Коллапс Мюзикл Норд - Ост, по роману Вениамина Каверина Два капитана
Мюзикл Норд - Ост, по роману Вениамина Каверина Два капитана Вимірювання потужності. Вимірювачі іімпульсної, середньої і великої потужності. (Тема 11.3)
Вимірювання потужності. Вимірювачі іімпульсної, середньої і великої потужності. (Тема 11.3) Урок по краеведению климат Карабаша
Урок по краеведению климат Карабаша Плюсы и минусы дистанционного образования
Плюсы и минусы дистанционного образования Конспект урока географии 6 класс Биосфера – сфера жизни Центры происхождения культурных растений (на основе системно-деятельностного подхода) Учебник: География.5-6 класс. Авторы: А.И.Алексеев, Е.К.Липкина В.В.Николина;
Конспект урока географии 6 класс Биосфера – сфера жизни Центры происхождения культурных растений (на основе системно-деятельностного подхода) Учебник: География.5-6 класс. Авторы: А.И.Алексеев, Е.К.Липкина В.В.Николина; terapiya ppt
terapiya ppt Природа Новосибирской области. Урок-игра
Природа Новосибирской области. Урок-игра Система маслоснабжения генератора
Система маслоснабжения генератора Компания ЗапСибЛогистика
Компания ЗапСибЛогистика 22 июня 1941 год
22 июня 1941 год