Содержание
- 2. Происхождение производной. В конце 17 века в Европе образовались две крупные математические школы. Главой одной из
- 3. Исаак Ньютон (1643 – 1727) Готфрид Вильгельм Лейбниц (1646 – 1716)
- 4. Происхождение производной. Ряд задач дифференциального исчисления был решен еще в древности. Такие задачи можно найти у
- 5. Памятник Ньютону в Кэмбридже.
- 6. Ньютон пришел к понятию производной, исходя из вопросов механики. Свои результаты в этой области он изложил
- 7. В подходе Лейбница к математическому анализу были некоторые особенности. Лейбниц мыслил высший анализ не кинематически, как
- 8. Памятник Лейбницу в Лейпциге.
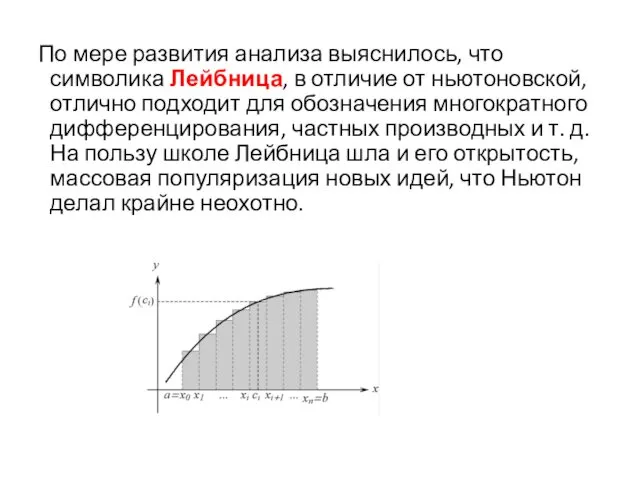
- 9. По мере развития анализа выяснилось, что символика Лейбница, в отличие от ньютоновской, отлично подходит для обозначения
- 10. Работы Лейбница по математике многочисленны и разнообразны. В 1666 году он написал первое сочинение: «О комбинаторном
- 11. В1672 году Лейбниц изобретает собственную конструкцию арифмометра, гораздо лучше паскалевской — он умел выполнять умножение, деление
- 12. Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке х этого
- 13. Нахождение производной называют дифференцированием
- 14. Таблица производных
- 15. Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 16. Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 17. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 18. Примеры
- 19. Примеры
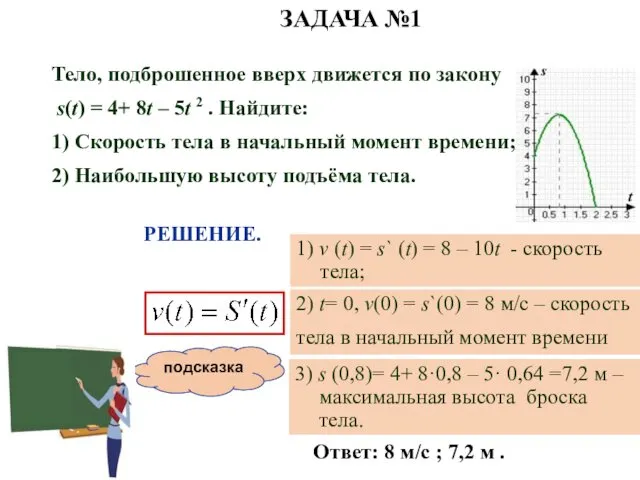
- 20. подсказка Тело, подброшенное вверх движется по закону s(t) = 4+ 8t – 5t 2 . Найдите:
- 21. ЗАДАЧА №2 При каких значениях х значение производной функции равно 0
- 22. “При изучении наук примеры не менее поучительны, нежели правила” “Примеры учат больше, чем теория”. И. Ньютон
- 23. Примеры
- 25. Производная и ее применение
- 26. Правильный ответ Правильный ответ Правильный ответ Правильный ответ Правильный ответ Найдите производные функций:
- 27. Найдите производную функции(устно): а) у = 6х5 – 7х3 + 2х2 – 5, у/ = 30
- 28. Найдите производную функции(устно): Правильный ответ Правильный ответ Правильный ответ Правильный ответ
- 30. 3. 4. 5.
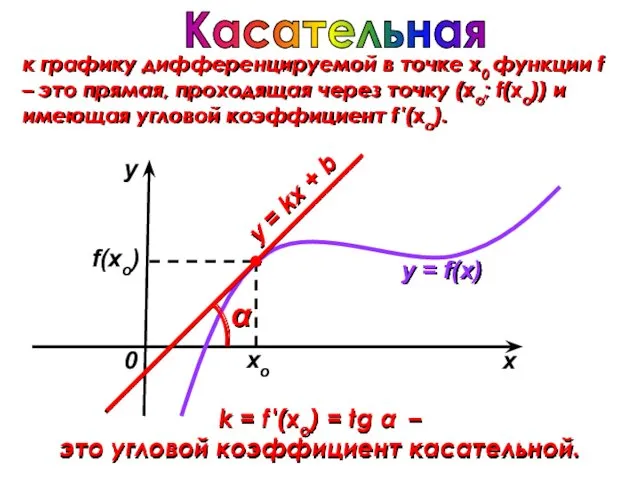
- 31. k = f ′(xo) = tg α – это угловой коэффициент касательной. f(xo) Касательная к графику
- 32. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 33. Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания. Признак возрастания
- 34. Алгоритм решения неравенств методом интервалов: Выделить функцию y=f(x). Найти область определения функции D(f). Указать промежутки непрерывности.
- 35. Решите неравенство: 1. 2x+5≠0, х ≠-2,5 2. f(x)=0, если x1= 8, x2= -2 3. Ответ:
- 36. Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x): Найти производную функции f´(x). Решить уравнение f´ (x) =0.
- 37. Найдите промежутки возрастания и убывания функции: 1. 2. f´(x)=0, если 3. Ответ:
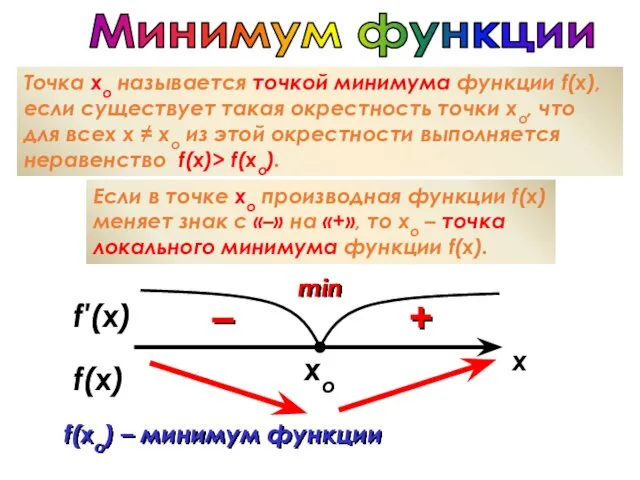
- 38. f′(x) xo Минимум функции Точка хо называется точкой минимума функции f(x), если существует такая окрестность точки
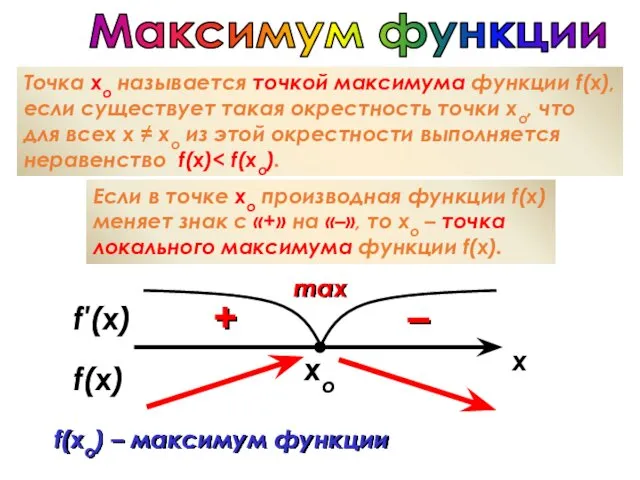
- 39. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
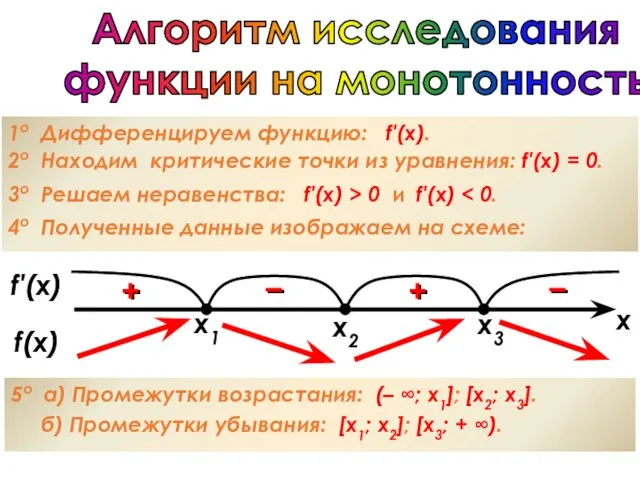
- 40. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
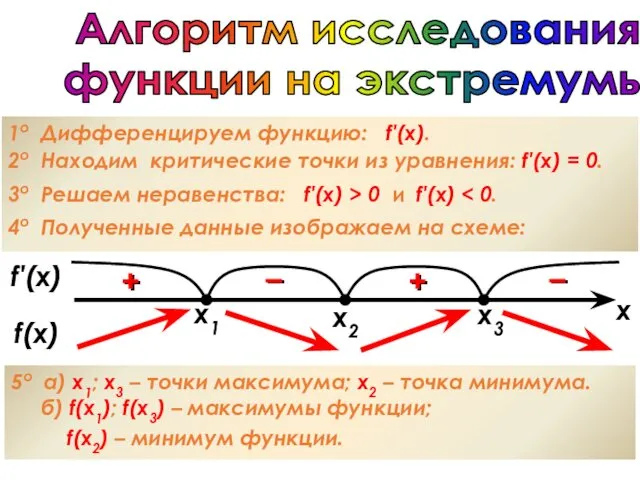
- 41. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 42. Примеры
- 44. + + + – –
- 47. Скачать презентацию




















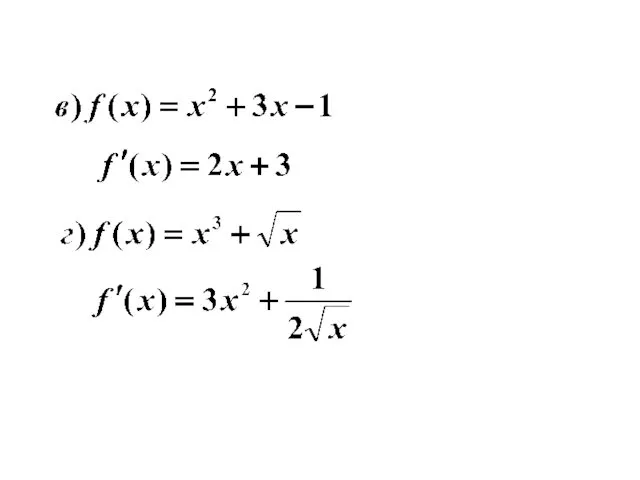
















 Физиология растений
Физиология растений Фрезерование. Выбор шага зубьев
Фрезерование. Выбор шага зубьев Элементы комплексного благоустройства объекта: лесопарк Сосновка
Элементы комплексного благоустройства объекта: лесопарк Сосновка Шесть самых провальных строительных проектов мира. Самые большие и самые смелые проекты на планете
Шесть самых провальных строительных проектов мира. Самые большие и самые смелые проекты на планете Компьютерное моделирование швейных изделий
Компьютерное моделирование швейных изделий Поисковый проект Я помню! Я горжусь!
Поисковый проект Я помню! Я горжусь! Пневмонии. Классификация пневмонии
Пневмонии. Классификация пневмонии Ударные и безударные слоги
Ударные и безударные слоги Презентация к обобщающему уроку по теме АТМОСФЕРА 6 класс
Презентация к обобщающему уроку по теме АТМОСФЕРА 6 класс 20231001_zemnovodnye_tulskoy_oblasti
20231001_zemnovodnye_tulskoy_oblasti Памятники воинам, погибшим в годы войны, в селе Кижинга и работа по их содержанию
Памятники воинам, погибшим в годы войны, в селе Кижинга и работа по их содержанию Конфликт как социально-психологическая проблема
Конфликт как социально-психологическая проблема Выступление на методическом собрании.
Выступление на методическом собрании. Сестринская помощь при ишурии (острая задержка мочи)
Сестринская помощь при ишурии (острая задержка мочи) Статистика ЕГЭ. Результаты ЕГЭ по физике 2018 года и перспективы 2019 года
Статистика ЕГЭ. Результаты ЕГЭ по физике 2018 года и перспективы 2019 года Технические основы блокчейн-технологий и криптовалют
Технические основы блокчейн-технологий и криптовалют 290 лет Колпино
290 лет Колпино Микрофлора воздуха
Микрофлора воздуха Проект внедрения технологии ADSL в микрорайоне X
Проект внедрения технологии ADSL в микрорайоне X Экосистема. Виды взаимодействия
Экосистема. Виды взаимодействия Способы сглаживания последствий хронического недосыпания
Способы сглаживания последствий хронического недосыпания программа кружка Умелые руки (детский сад)
программа кружка Умелые руки (детский сад) Чувствительность
Чувствительность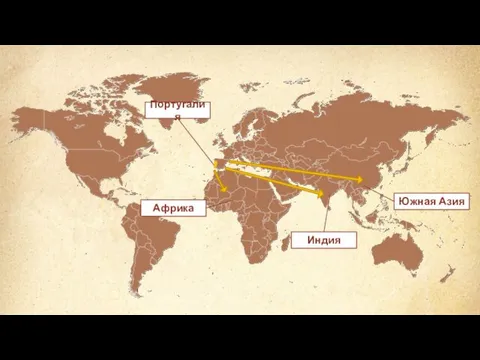 Начало колониальных захватов и создания колониальных империй
Начало колониальных захватов и создания колониальных империй Правила надлежащей производственной практики применительно к биотехнологии. Международные стандарты GMP
Правила надлежащей производственной практики применительно к биотехнологии. Международные стандарты GMP Дидактические игры как средство развития познавательной активности детей
Дидактические игры как средство развития познавательной активности детей Подарок своими руками
Подарок своими руками Ипользование инновационных и традиционных пед. технологий в начальной школе ( из опыта работы)
Ипользование инновационных и традиционных пед. технологий в начальной школе ( из опыта работы)