Содержание
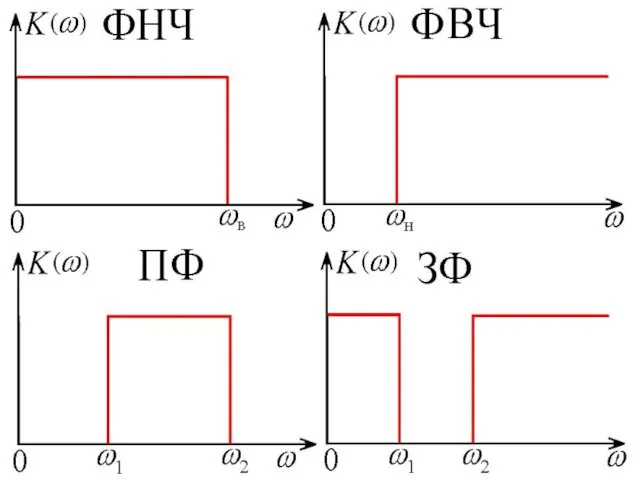
- 2. Радиотехнические цепи и сигналы Целью курса является изучение фундаментальных закономерностей, связанных с анализом и синтезом сигналов,
- 3. Программа 1. Канал связи, его составные части. 2. Свойства сигналов: длительность, динамический диапазон, энергия, мощность, ортогональность
- 4. 16. Дискретизация непрерывных сигналов. Теорема Котельникова во временной и частотной областях. 17. Аналого-цифровые и цифро-аналоговые преобразования.
- 5. Литература Иванов М.Т., Сергиенко А.Б., Ушаков В.Н. Теоретические основы радиотехники. – М.: Высшая школа, 2008. –
- 9. Важнейшие физические характеристики сигнала: длительность, энергия, динамический диапазон Реальные сигналы обладают конечной длительностью (t2 – t1).
- 10. Энергия сигнала определяется как
- 11. Допустимы линейные операции над сигналами: 1. Для всех Si(t),Sj(t) существует сумма S(t)=Si(t)+Sj(t), равенство должно выполняться для
- 12. Расстояние между сигналами Si(t) и Sj(t) Скалярное произведение вещественных сигналов Скалярное произведение комплексных сигналов
- 13. Скалярное произведение двух ортогональных сигналов равно (fi, fj ) = 0, если i ≠ j; (fi,
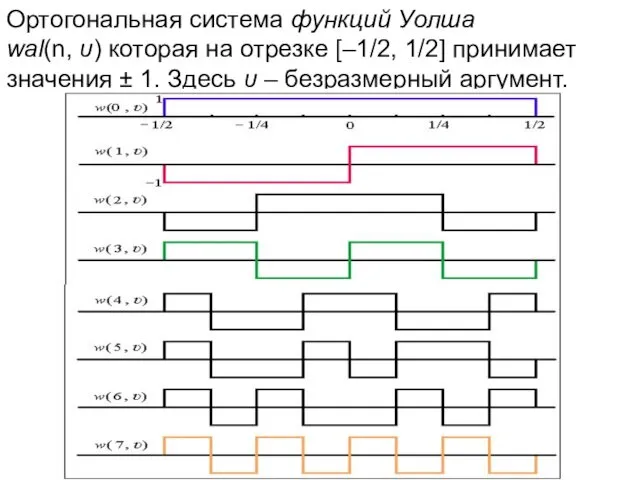
- 14. Ортогональная система функций Уолша wal(n, υ) которая на отрезке [–1/2, 1/2] принимает значения ± 1. Здесь
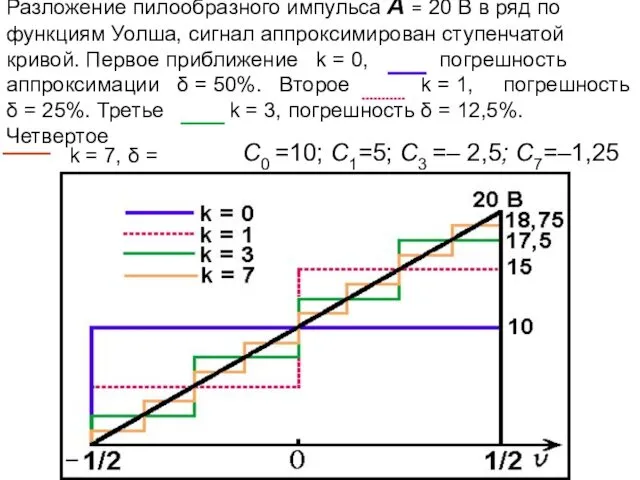
- 15. Разложение пилообразного импульса А = 20 В в ряд по функциям Уолша, сигнал аппроксимирован ступенчатой кривой.
- 16. Наиболее распространена система ортогональных тригонометрических функций. Любая периодическая функция s(t) с периодом T, с конечной энергией
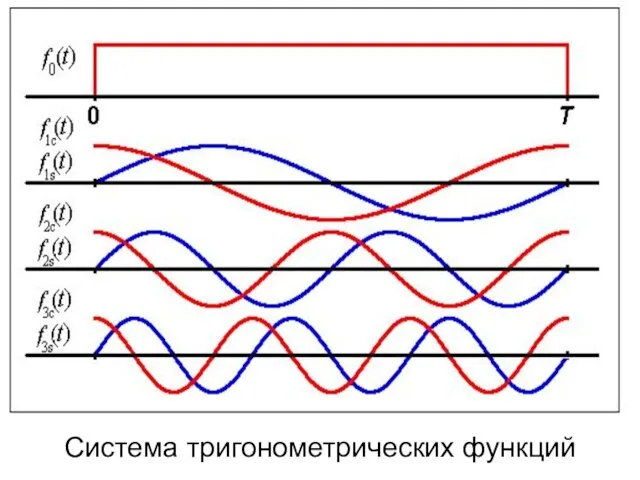
- 17. Система тригонометрических функций
- 18. с0 – «постоянная составляющая» сигнала сn –амплитуда n-ой гармонической составляющей с частотой ωn = nω0 и
- 19. Экспоненциальная форма тригонометрического ряда Фурье где j – мнимая единица. Положим φ–n = – φn
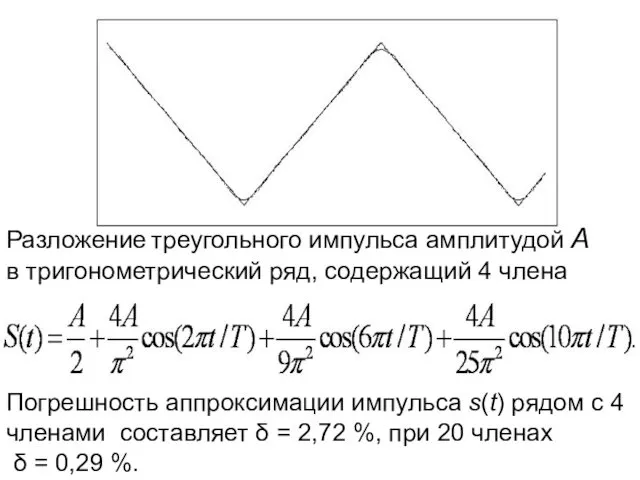
- 20. Разложение треугольного импульса амплитудой А в тригонометрический ряд, содержащий 4 члена Погрешность аппроксимации импульса s(t) рядом
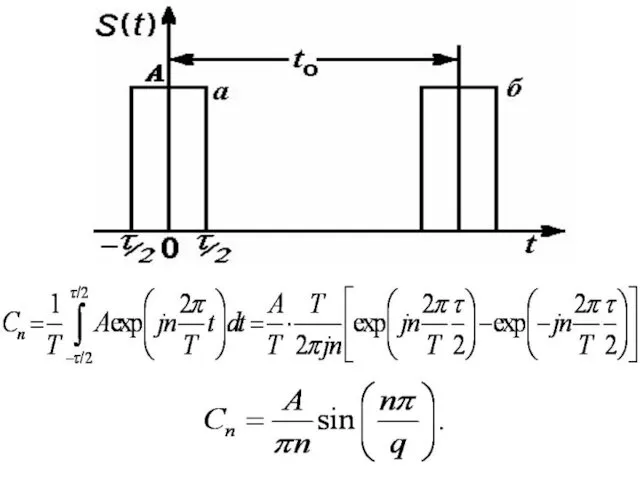
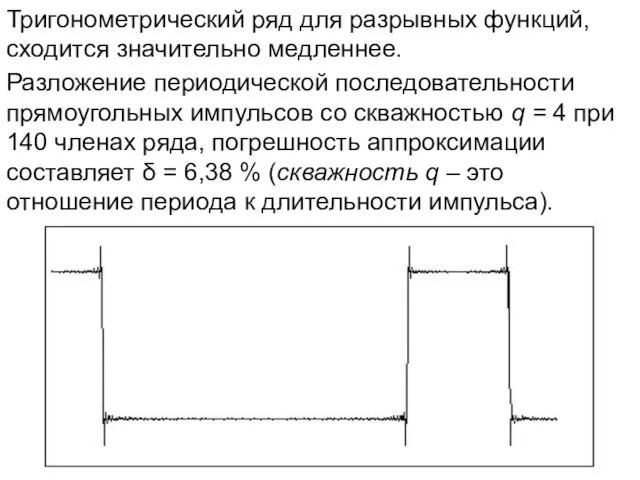
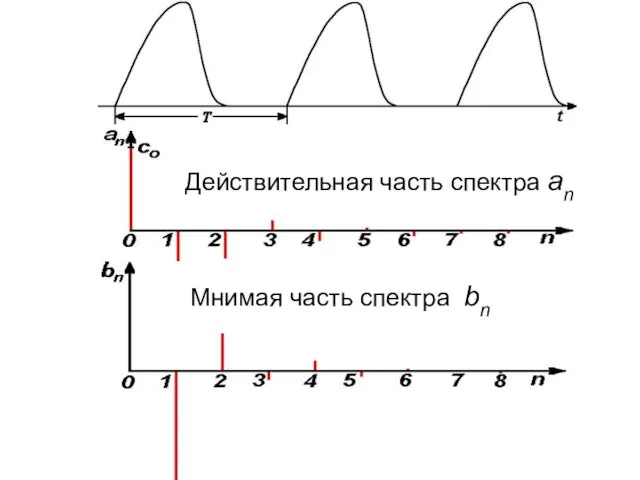
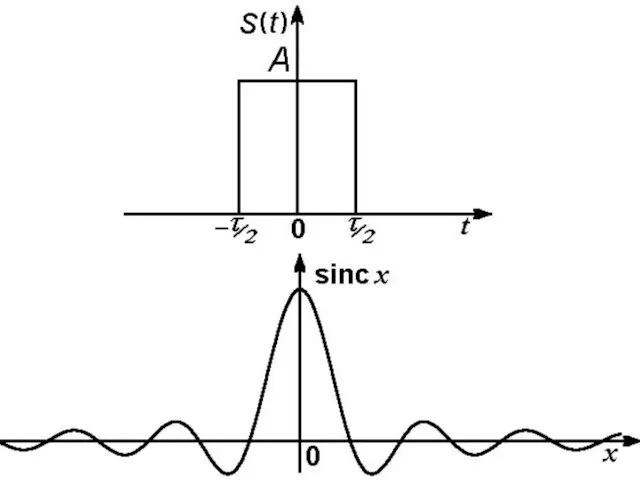
- 22. Тригонометрический ряд для разрывных функций, сходится значительно медленнее. Разложение периодической последовательности прямоугольных импульсов со скважностью q
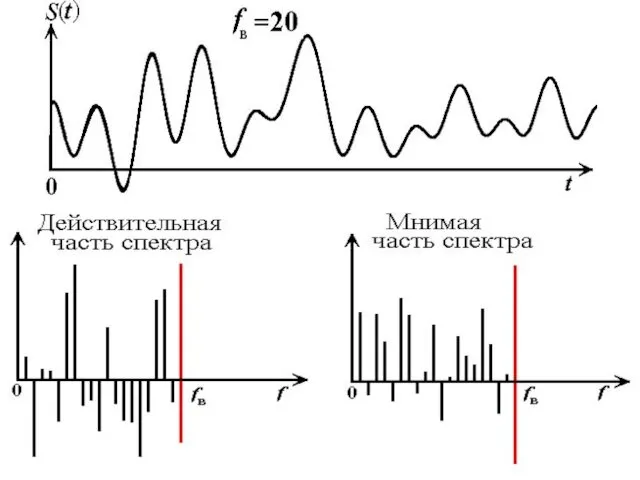
- 23. Действительная часть спектра an Мнимая часть спектра bn
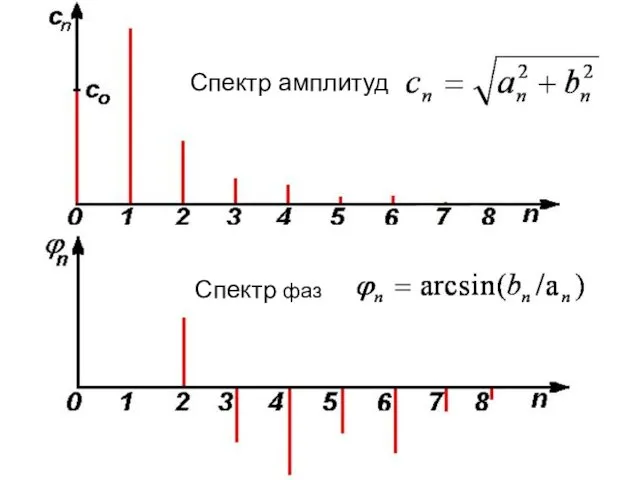
- 24. Спектр амплитуд Спектр фаз
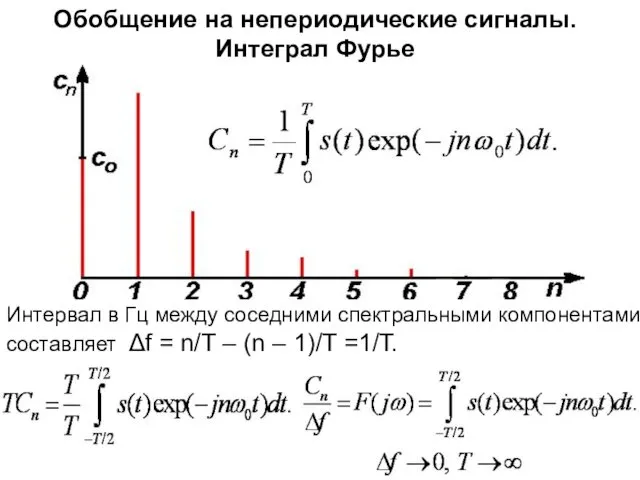
- 25. Обобщение на непериодические сигналы. Интеграл Фурье Интервал в Гц между соседними спектральными компонентами составляет Δf =
- 26. Устремим Δf 0 . Предельный переход имеет смысл, так как
- 27. Свойства преобразования Фурье 1. Преобразование Фурье – линейное, так как интегралы Фурье – это предел суммы.
- 28. Из равенства нулю мнимой части и ортогональности функций cosωt и sinωt следует, что A(ω) = A(–ω),
- 30. 5. Из п.4 следует, что длительность сигнала и ширина спектра связаны между собой. Произведение ΔΩ ·ΔT
- 31. Наличие пиков указывает на периодичность. Одна из причин применения ряда Фурье и интеграла Фурье – необходимость
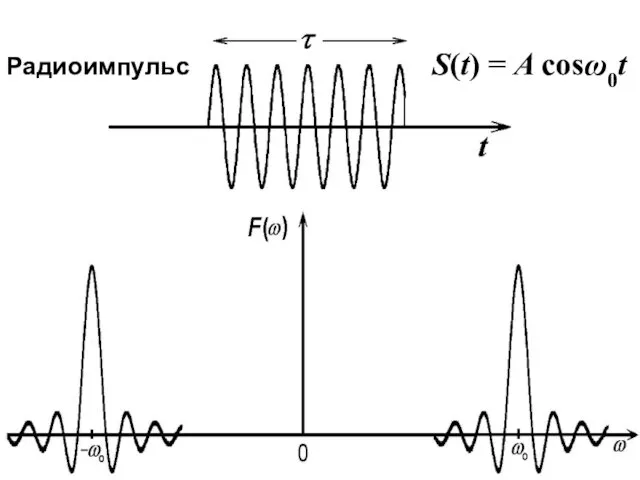
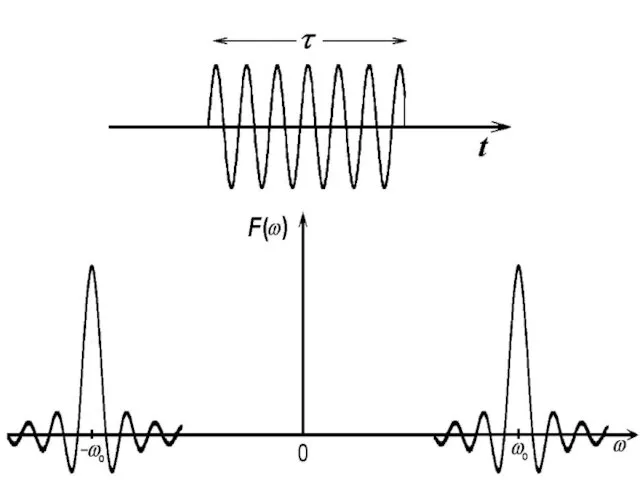
- 32. S(t) = A cosω0t Радиоимпульс
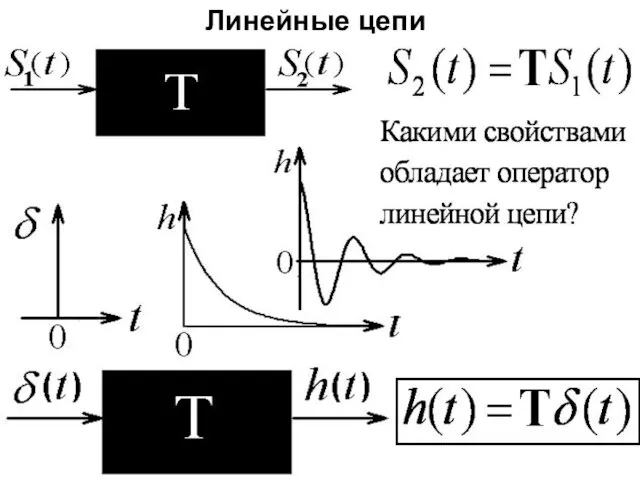
- 33. Линейные цепи
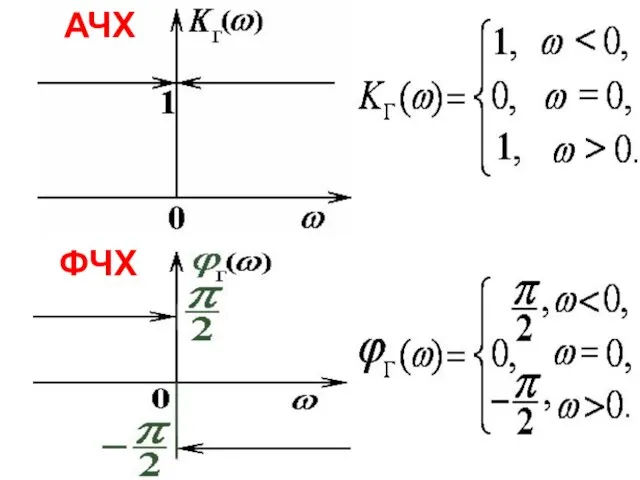
- 35. АЧХ ФЧХ Амплитудно-частотная характеристика показывает, как изменилась амплитуда Фазо-частотная характеристика показывает величину задержки фазы на выходе
- 36. Сигналы несинусоидальной формы искажаются линейными цепями. У сигналов синусоидальной формы изменяется амплитуда, происходит задержка по фазе,
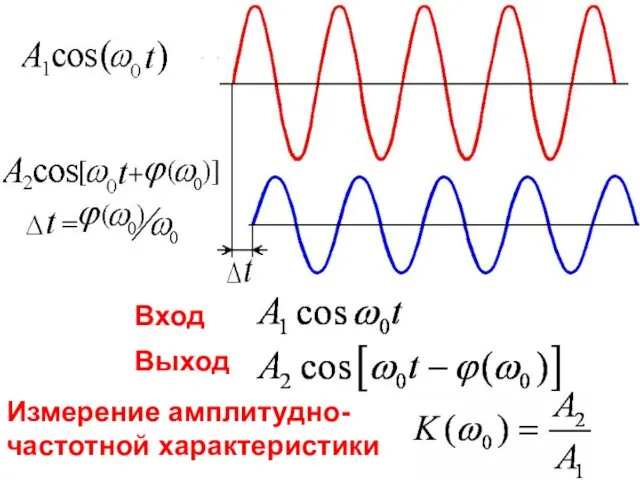
- 37. Вход Выход Измерение амплитудно- частотной характеристики
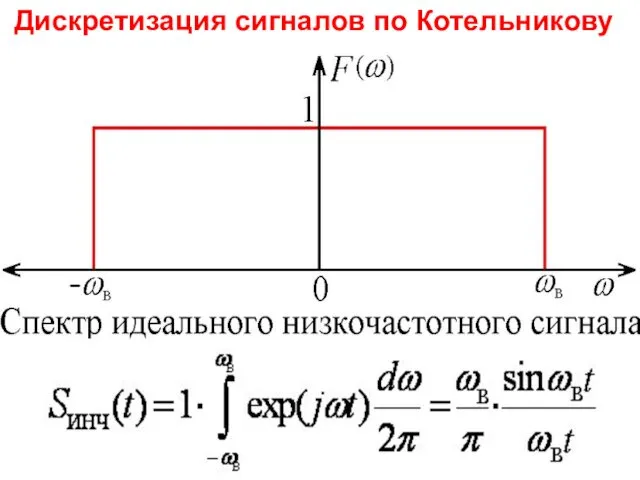
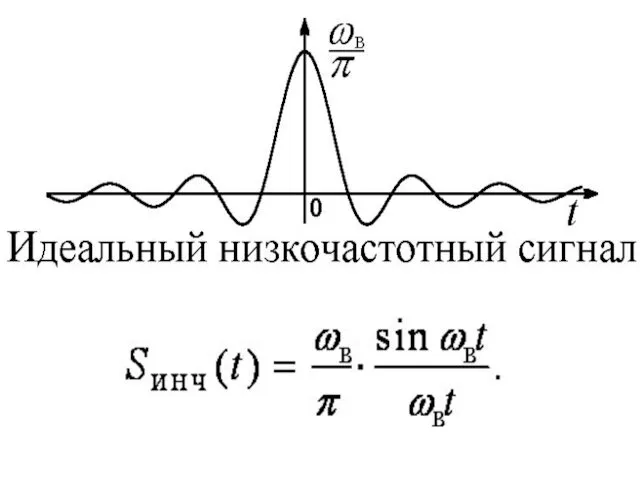
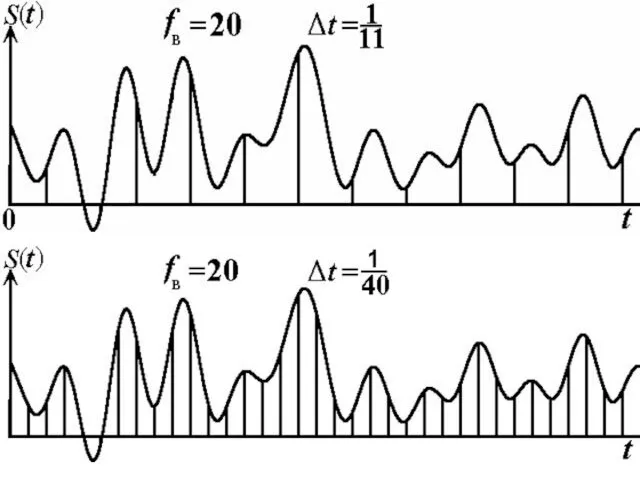
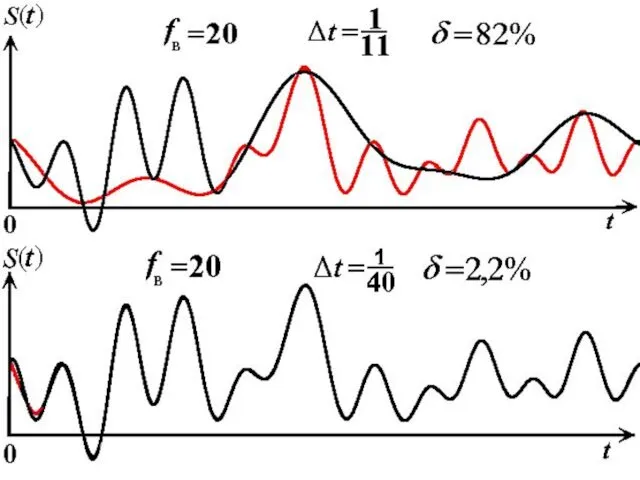
- 40. Дискретизация сигналов по Котельникову
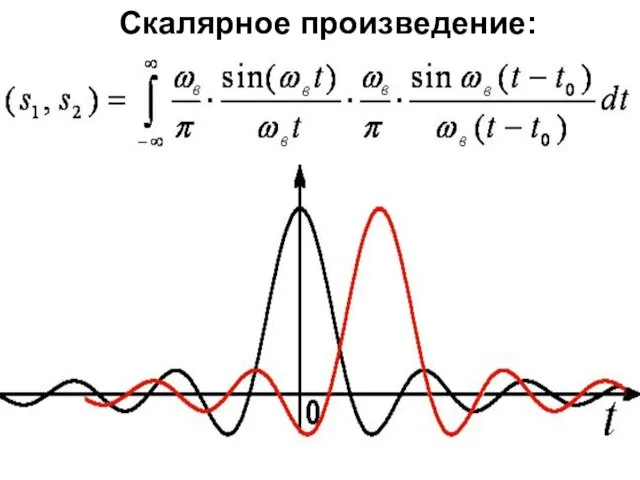
- 42. Скалярное произведение:
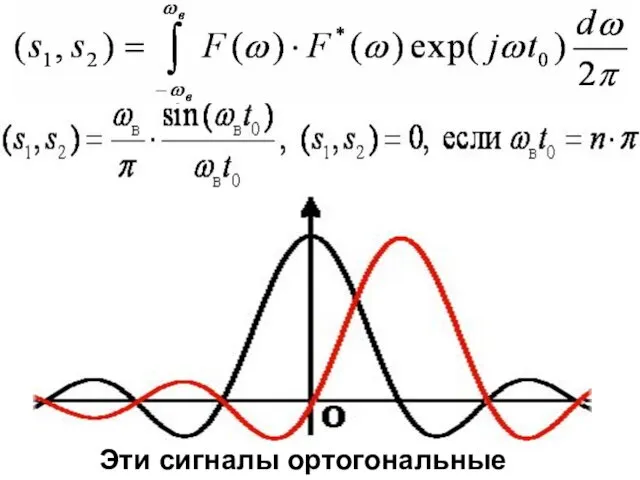
- 43. Эти сигналы ортогональные
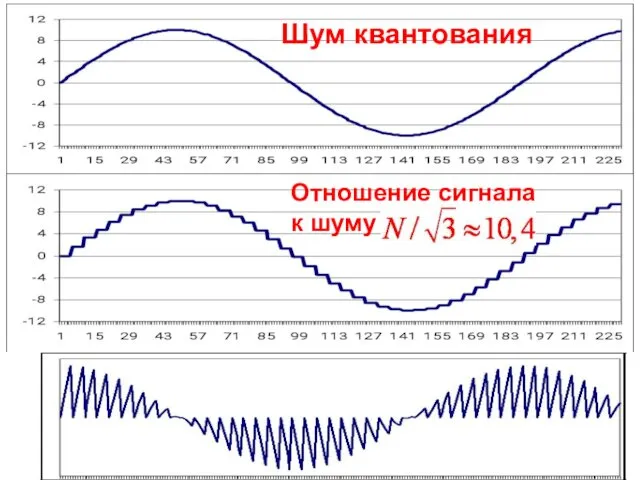
- 48. Отношение сигнала к шуму Шум квантования
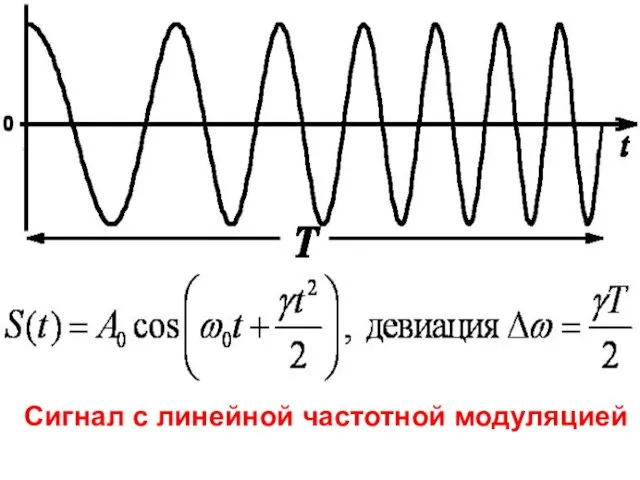
- 54. Сигнал с линейной частотной модуляцией
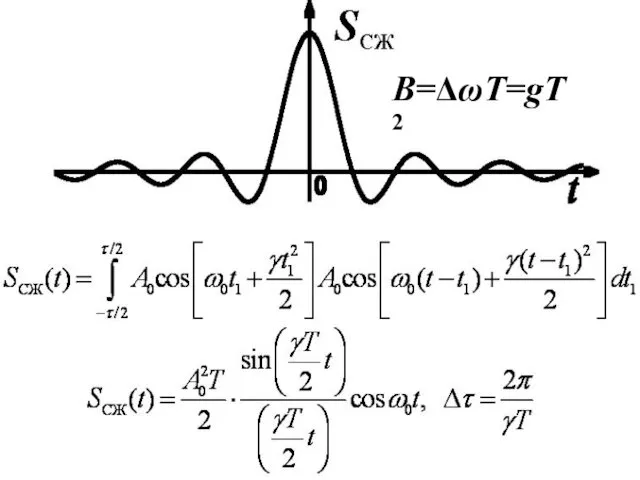
- 56. Β=ΔωT=gT2
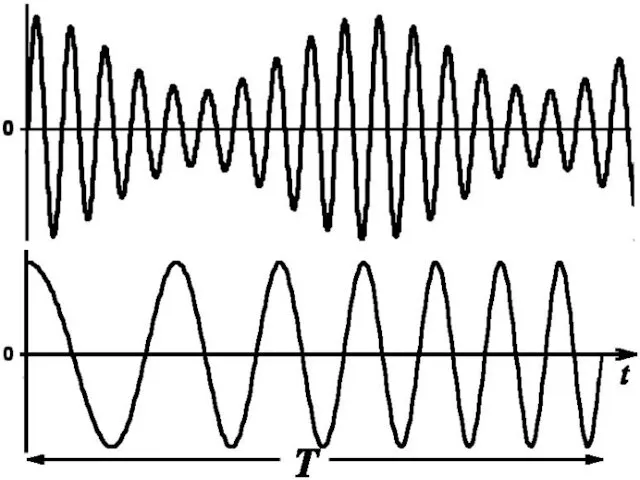
- 58. ОГИБАЮЩАЯ U(t)
- 62. АЧХ ФЧХ
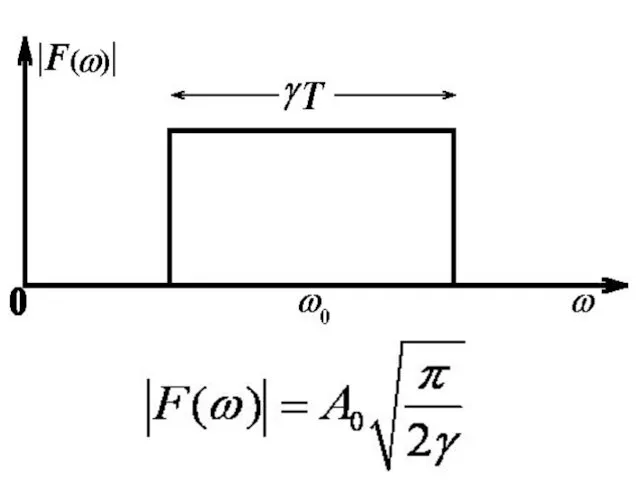
- 67. Спектр аналитического сигнала
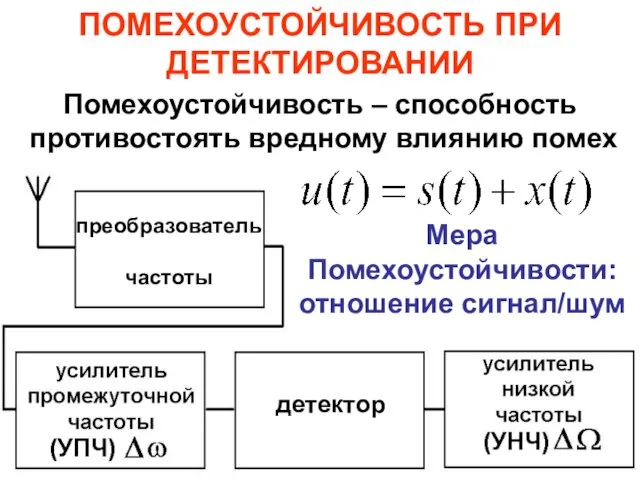
- 68. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ДЕТЕКТИРОВАНИИ Помехоустойчивость – способность противостоять вредному влиянию помех преобразователь частоты детектор Мера Помехоустойчивости: отношение
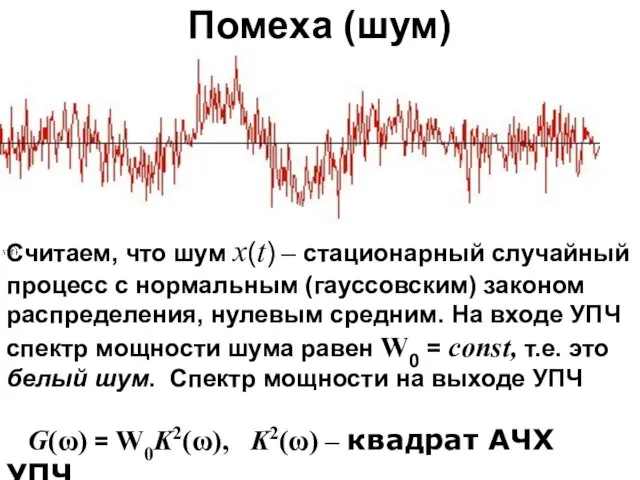
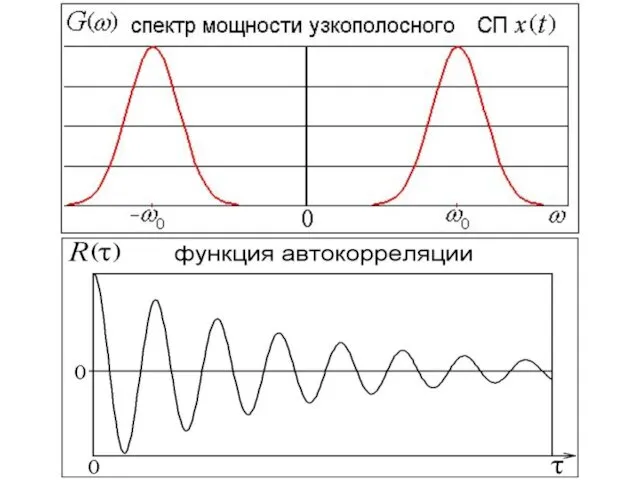
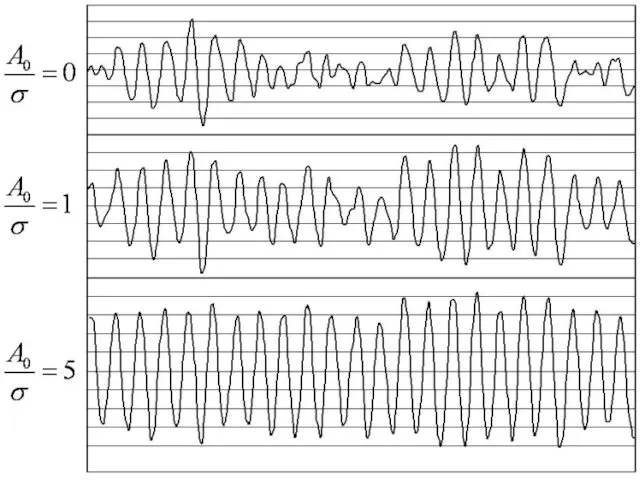
- 69. Помеха (шум) Считаем, что шум x(t) – стационарный случайный процесс с нормальным (гауссовским) законом распределения, нулевым
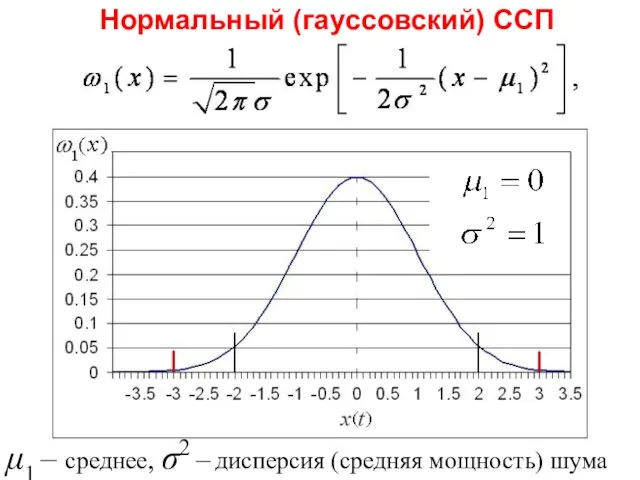
- 70. Нормальный (гауссовский) ССП μ1 – среднее, σ2 – дисперсия (средняя мощность) шума
- 71. По теореме Винера-Хинчина
- 73. Для белого шума
- 74. Фазовый детектор Вход: отношение несущая/шум
- 75. После ограничителя U(t) = U0 = const
- 79. Сигнал амплитудная импульсная модуляция
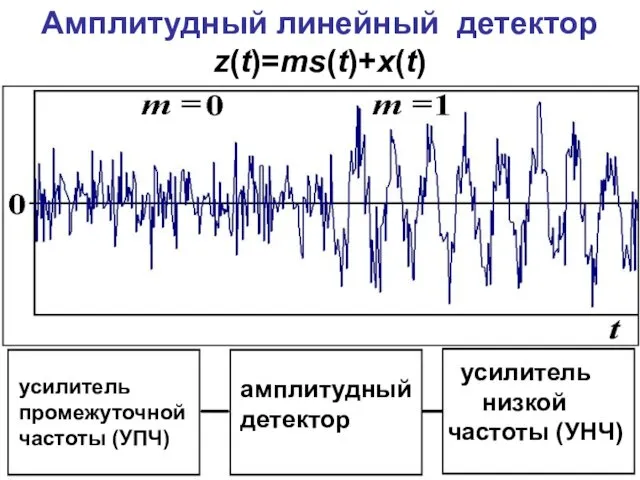
- 80. Амплитудный линейный детектор z(t)=ms(t)+x(t) усилитель промежуточной частоты (УПЧ) амплитудный детектор усилитель низкой частоты (УНЧ)
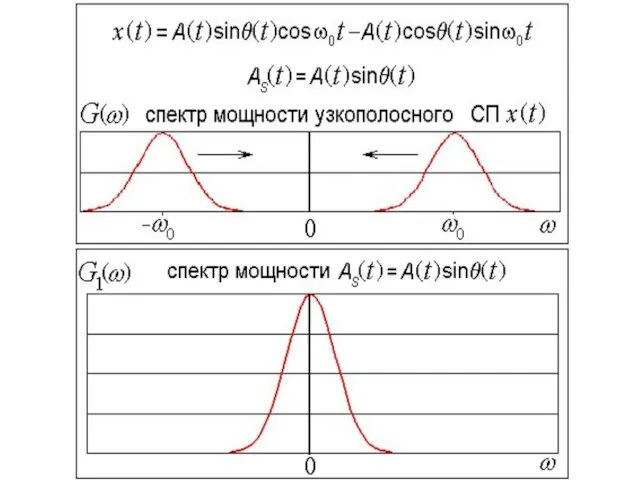
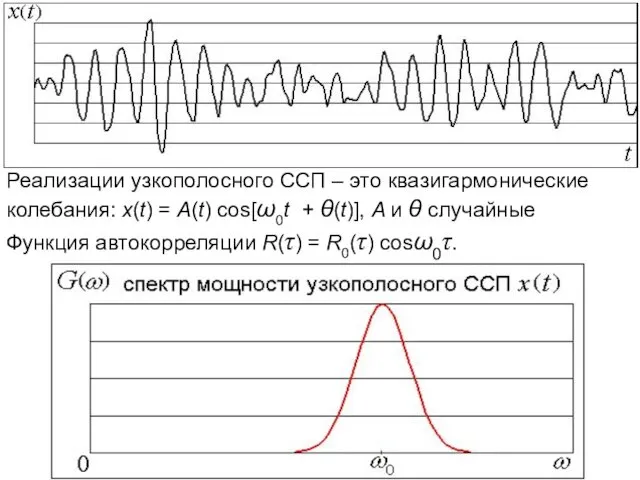
- 81. Реализации узкополосного ССП – это квазигармонические колебания: x(t) = A(t) cos[ω0t + θ(t)], A и θ
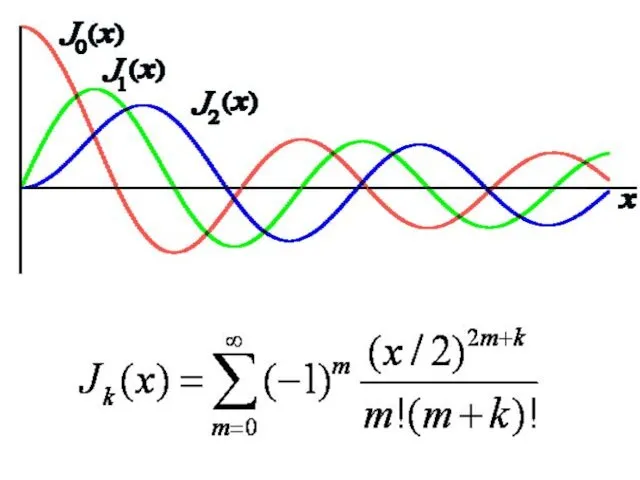
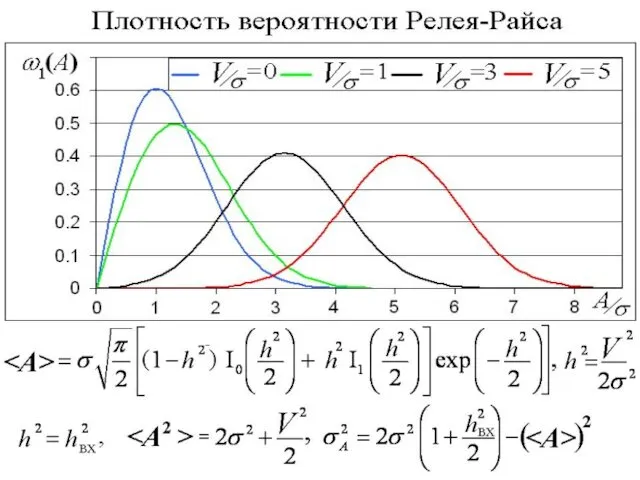
- 87. Отношение сигнала к шуму на выходе линейного детектора Функция Бесселя от мнимого аргумента Функция Бесселя от
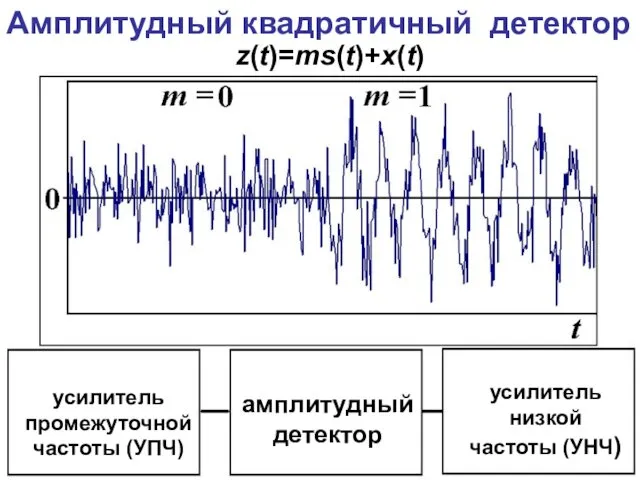
- 90. усилитель промежуточной частоты (УПЧ) амплитудный детектор усилитель низкой частоты (УНЧ) Амплитудный квадратичный детектор z(t)=ms(t)+x(t)
- 94. Скачать презентацию









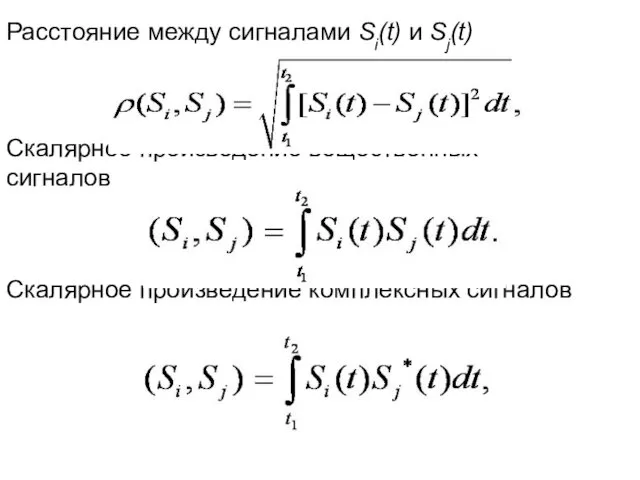




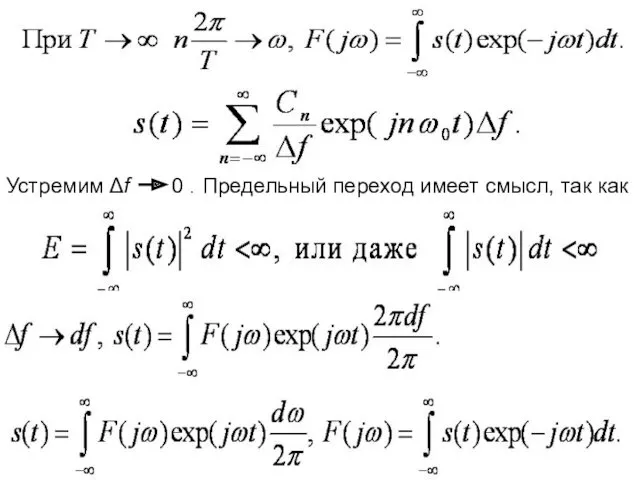




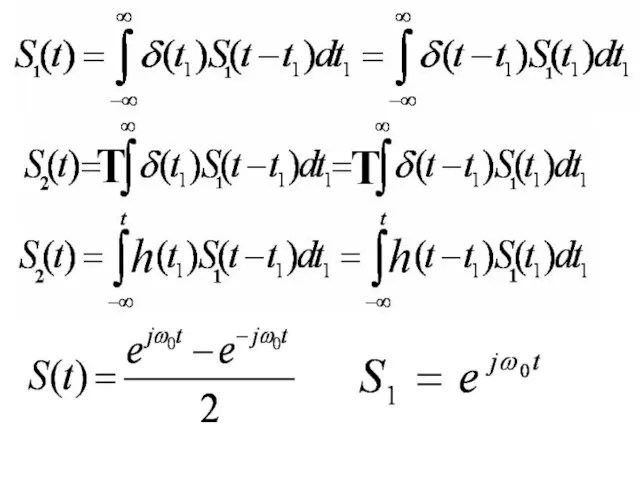


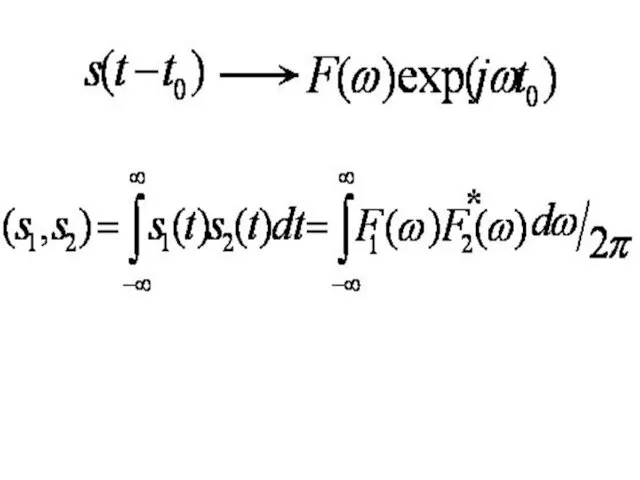
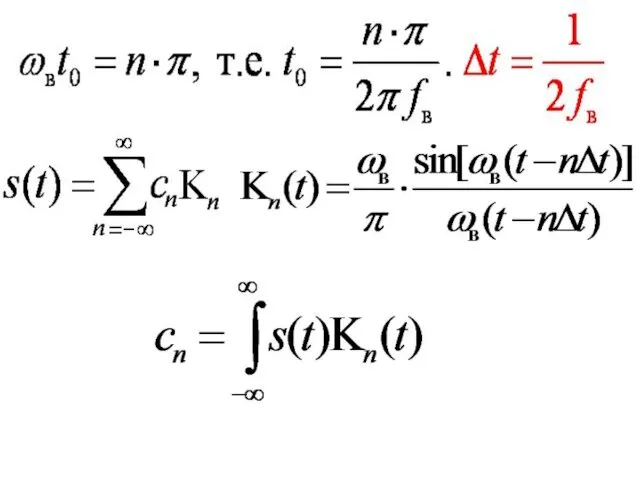
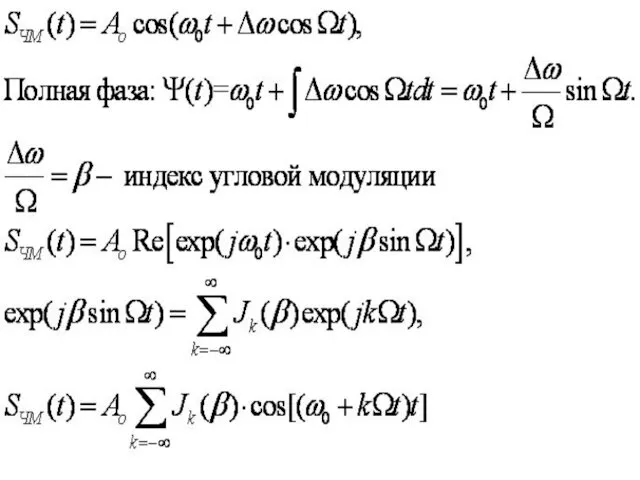

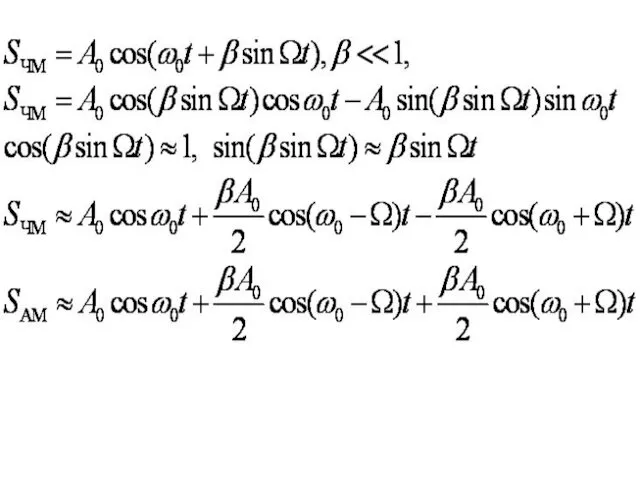






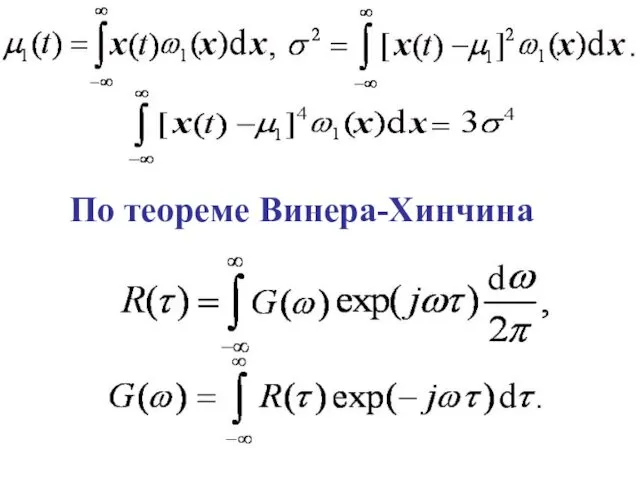



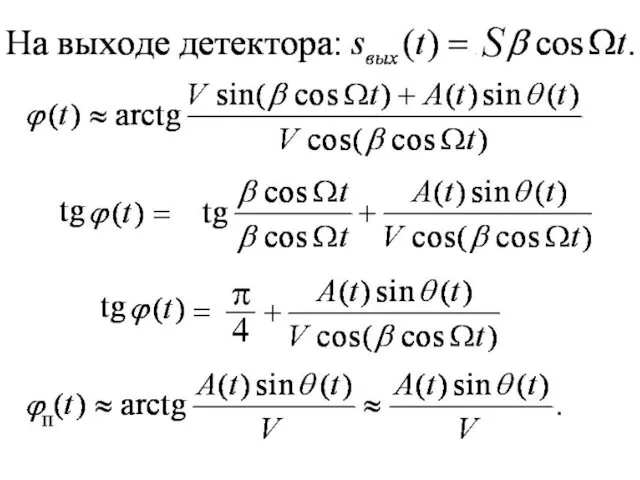


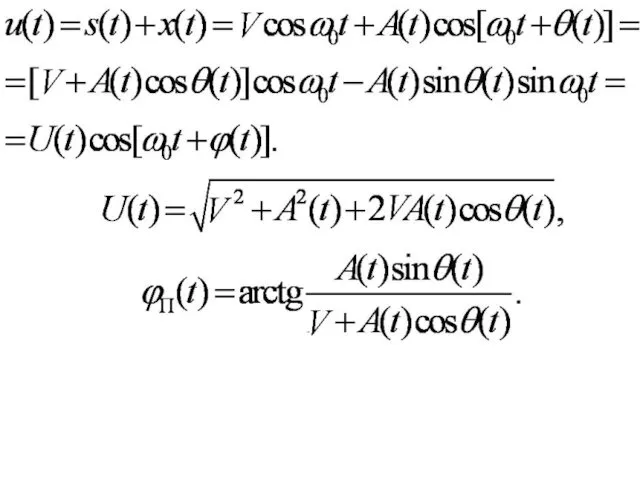


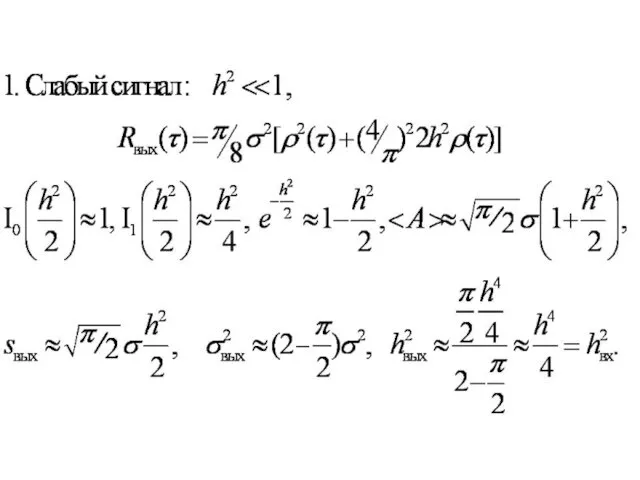
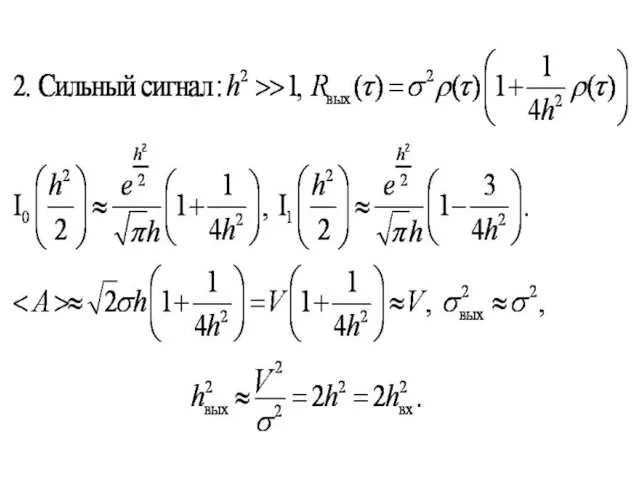
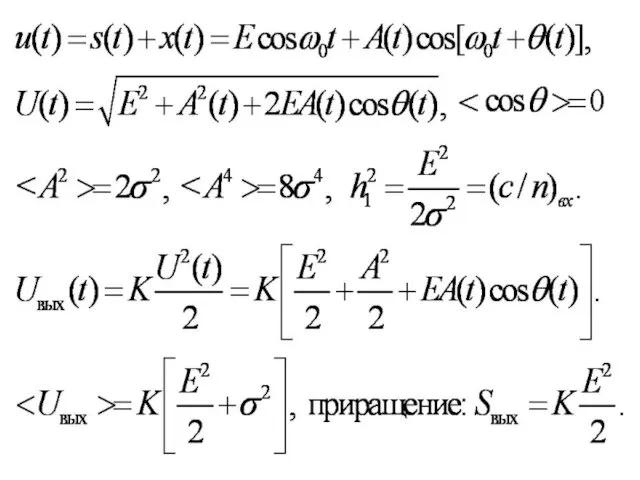
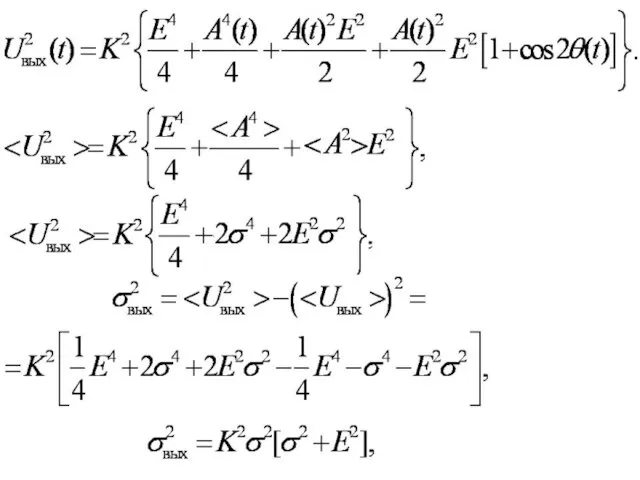
 Теории мотивации
Теории мотивации Визитка для участника интернет-проекта Путешествие в мир химии
Визитка для участника интернет-проекта Путешествие в мир химии Первые представления о решении рациональных уравнений
Первые представления о решении рациональных уравнений Средства и устройства пожаротушения
Средства и устройства пожаротушения Первый закон термодинамики
Первый закон термодинамики gimnastika_dlya_glaz_zvezdochet
gimnastika_dlya_glaz_zvezdochet Логопедическое занятие: Нахождение приставки в словах.
Логопедическое занятие: Нахождение приставки в словах. Числовые ряды
Числовые ряды Сценарий праздника До свидания, первый класс!
Сценарий праздника До свидания, первый класс! Гепатит. Классификация гепатита
Гепатит. Классификация гепатита Горячие сладкие блюда
Горячие сладкие блюда Прямоугольный параллелепипед
Прямоугольный параллелепипед Презентация к статье
Презентация к статье Зарядка для пальчиков
Зарядка для пальчиков Положение рабов в Древнем Риме
Положение рабов в Древнем Риме Цифровые последовательностные устройства. Тема 4.3
Цифровые последовательностные устройства. Тема 4.3 Family_Guess who
Family_Guess who GPS и все такое прочее
GPS и все такое прочее Внутреннее устройство компьютера
Внутреннее устройство компьютера Индикация формируемого маршрута. Работа схем в различных режимах
Индикация формируемого маршрута. Работа схем в различных режимах Формирование сенсорных эталонов формы и величины как основа формирования элементарных математических представлений детей 3-го года жизни
Формирование сенсорных эталонов формы и величины как основа формирования элементарных математических представлений детей 3-го года жизни Kesimlar. Kesim turlari.Kesimda shartlilik va soddalashtirishlar. Qirqimlar
Kesimlar. Kesim turlari.Kesimda shartlilik va soddalashtirishlar. Qirqimlar Сценарий и презентация праздника Проводы масленицы
Сценарий и презентация праздника Проводы масленицы Газообразное состояние вещества
Газообразное состояние вещества Топонимика мира: происхождение названия озёр
Топонимика мира: происхождение названия озёр Родительское собрание Детская агрессия
Родительское собрание Детская агрессия Сделки с заинтересованностью
Сделки с заинтересованностью Методи аналізу електричних кіл. Основні поняття електричних величин
Методи аналізу електричних кіл. Основні поняття електричних величин