Содержание
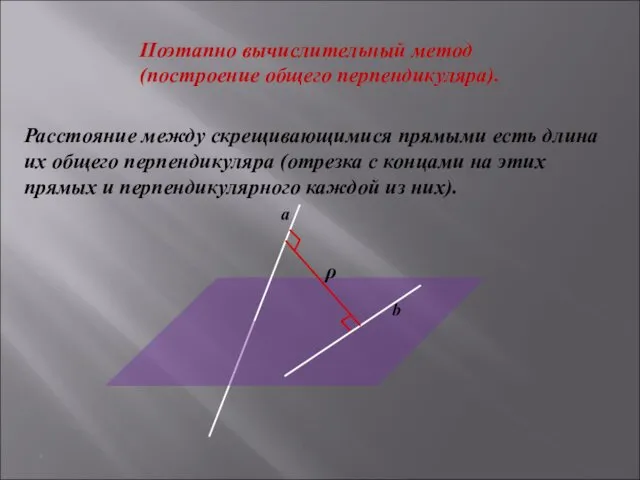
- 2. * Расстояние между скрещивающимися прямыми есть длина их общего перпендикуляра (отрезка с концами на этих прямых
- 3. * Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстоянию
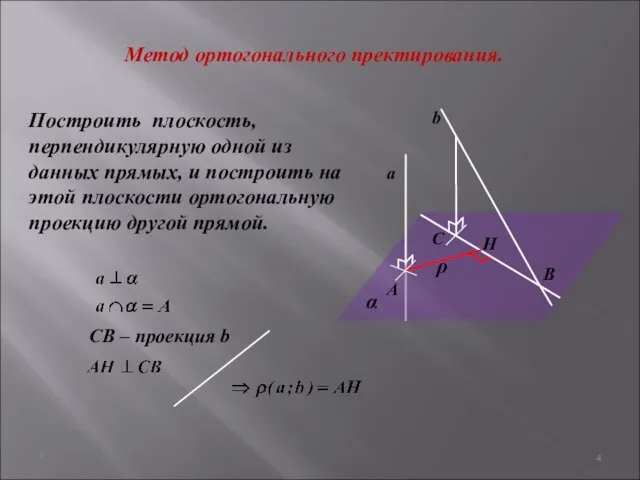
- 4. * Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию другой
- 5. * Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, d – расстояние между ними,
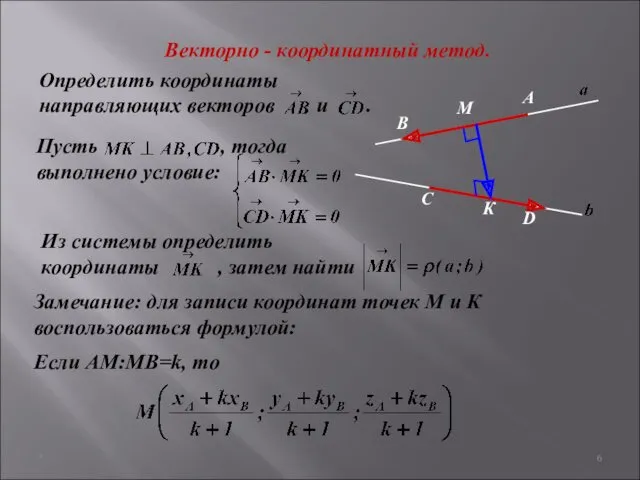
- 6. Из системы определить координаты , затем найти Пусть , тогда выполнено условие: * Определить координаты направляющих
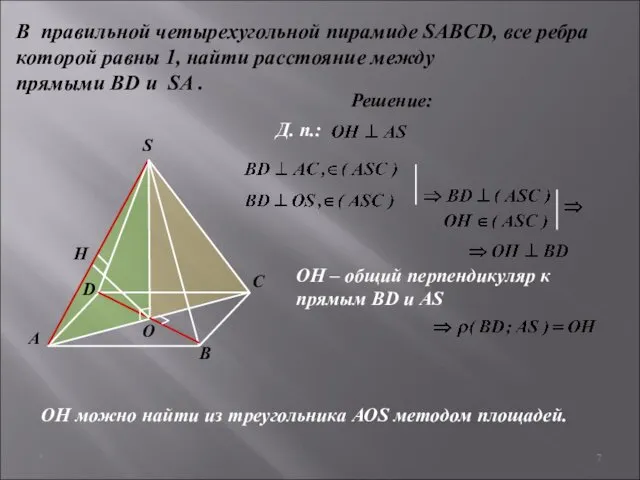
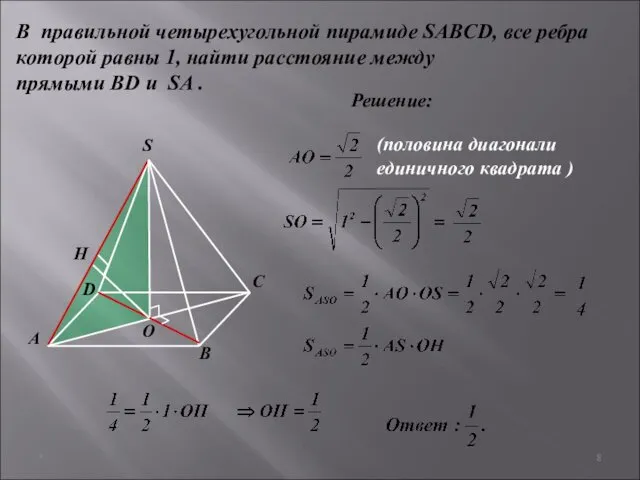
- 7. * В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти расстояние между прямыми BD
- 8. * В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти расстояние между прямыми BD
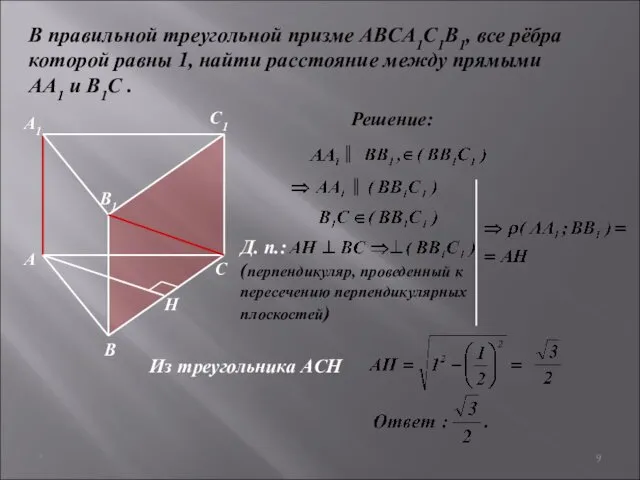
- 9. * В правильной треугольной призме ABCA1C1B1, все рёбра которой равны 1, найти расстояние между прямыми АA1
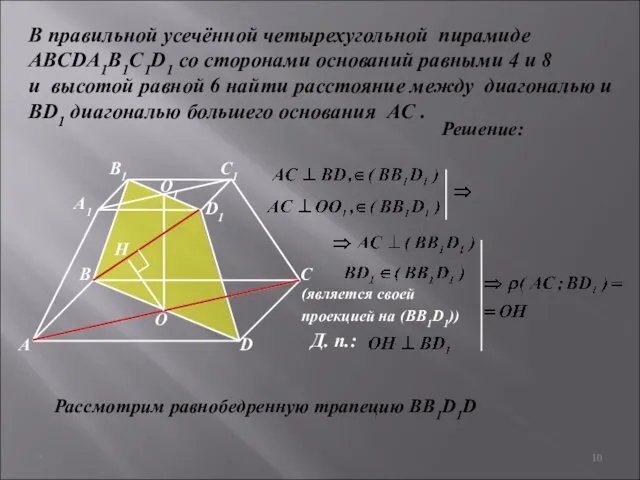
- 10. * В правильной усечённой четырехугольной пирамиде ABCDA1B1C1D1 со сторонами оснований равными 4 и 8 и высотой
- 11. * В правильной усечённой четырехугольной пирамиде ABCDA1B1C1D1 со сторонами оснований равными 4 и 8 и высотой
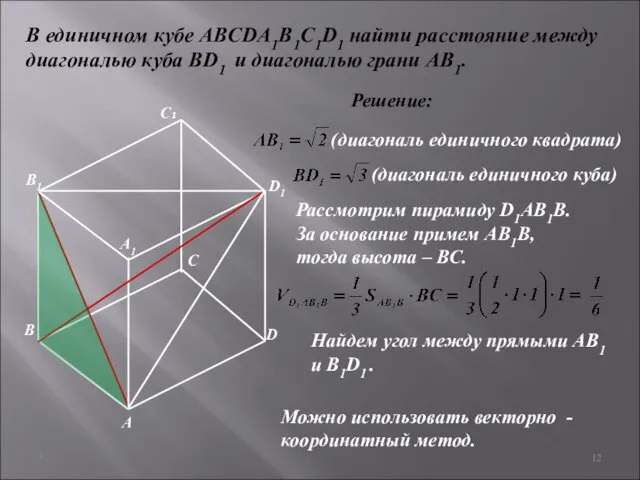
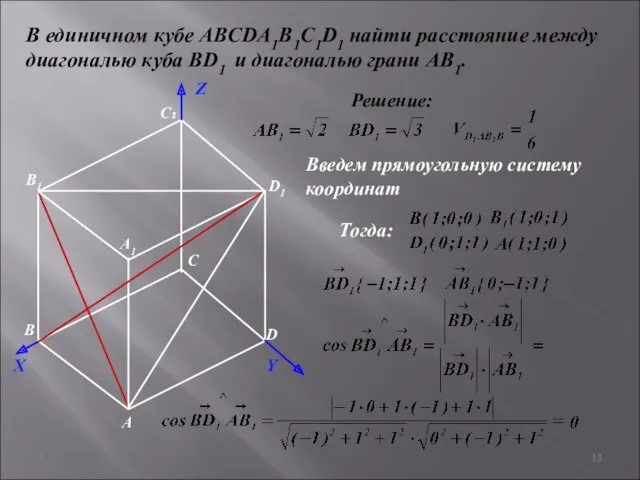
- 12. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1. Решение:
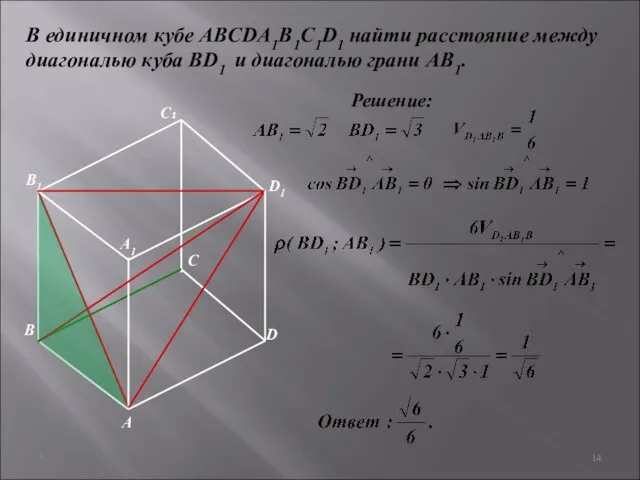
- 13. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1. Решение:
- 14. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1. Решение:
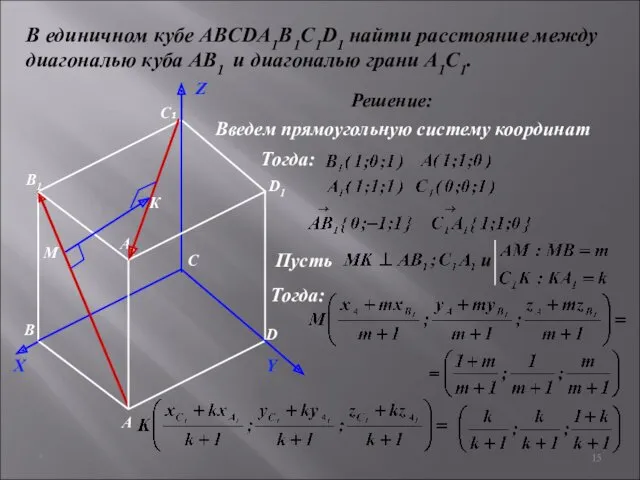
- 15. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба АВ1 и диагональю грани A1С1. Решение:
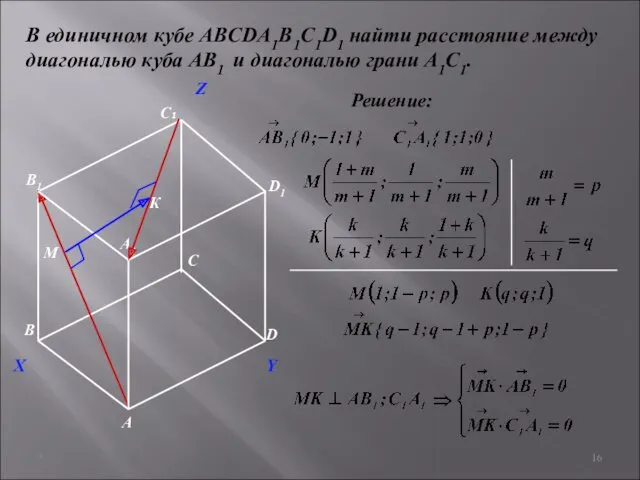
- 16. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба АВ1 и диагональю грани A1С1. Решение:
- 17. * В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба АВ1 и диагональю грани A1С1. Решение:
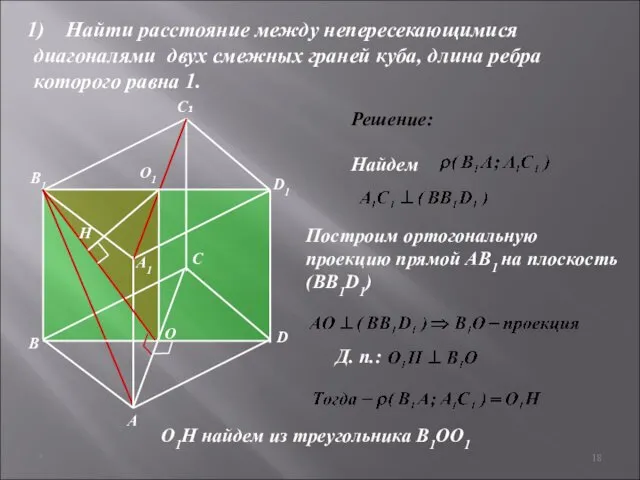
- 18. * Решение: Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна 1.
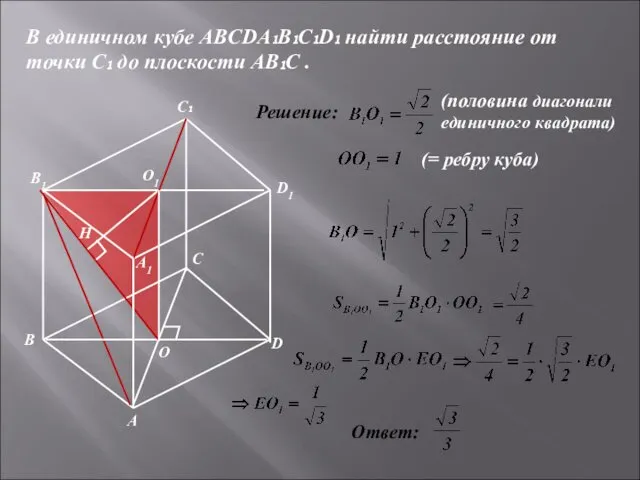
- 19. В единичном кубе ABCDA₁B₁C₁D₁ найти расстояние от точки С₁ до плоскости АВ₁С . (половина диагонали единичного
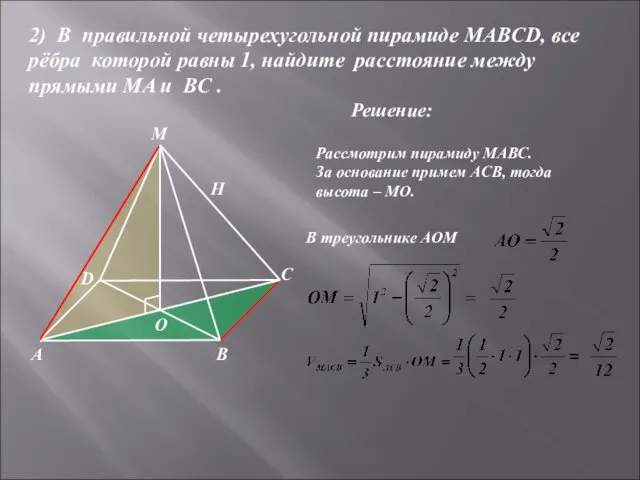
- 20. Решение: А D В С М О Н 2) В правильной четырехугольной пирамиде MABCD, все рёбра
- 22. Скачать презентацию




 Работа с программой Octopus и сайтом статистики
Работа с программой Octopus и сайтом статистики презентация к уроку технология УМК Гармония 1 класс Работа с разными материалами
презентация к уроку технология УМК Гармония 1 класс Работа с разными материалами Поисковая система Яндекс
Поисковая система Яндекс Презентация к уроку ОРКСЭ 4 класс Тема:Мусульманские праздники и памятные дни
Презентация к уроку ОРКСЭ 4 класс Тема:Мусульманские праздники и памятные дни 3D-моделирование
3D-моделирование О вреде использованных батареек для окружающей среды
О вреде использованных батареек для окружающей среды Западно-европейская традиция обращения философии к образованию и отечественная философская мысль об образовании
Западно-европейская традиция обращения философии к образованию и отечественная философская мысль об образовании Нарушение водно - солевого обмена
Нарушение водно - солевого обмена Дроби вокруг нас
Дроби вокруг нас Тәуелсіз Қазақстан тарихнамасында. Алаш қозғалысына байланысты еңбектерді талдау. Ә. Бөкейханов, М. Шоқай, А. Байтұрсынұлы
Тәуелсіз Қазақстан тарихнамасында. Алаш қозғалысына байланысты еңбектерді талдау. Ә. Бөкейханов, М. Шоқай, А. Байтұрсынұлы ВЗАИМОДЕЙСТВИЕ ОБЩЕСТВА И ПРИРОДЫ 10КЛ
ВЗАИМОДЕЙСТВИЕ ОБЩЕСТВА И ПРИРОДЫ 10КЛ Делимость чисел
Делимость чисел Планирование производства строительно-монтажных работ
Планирование производства строительно-монтажных работ Література і театр в 15- 16 ст. Стиль бароко
Література і театр в 15- 16 ст. Стиль бароко Развитие жизни на Земле. 9 класс
Развитие жизни на Земле. 9 класс Мал суару қөздері
Мал суару қөздері Высоковольтные электрические аппараты
Высоковольтные электрические аппараты Экологическое воспитание в современном ДОУ.
Экологическое воспитание в современном ДОУ. Музыка в движении. Попутная песня. Г.Свиридов М.Глинка
Музыка в движении. Попутная песня. Г.Свиридов М.Глинка Валютный курс как элемент валютной системы
Валютный курс как элемент валютной системы Phonics & Grammar
Phonics & Grammar Выбор эффективных строительных материалов для коттеджа
Выбор эффективных строительных материалов для коттеджа Материалы для подготовки к ЕГЭ по биологии, схемы и таблицы
Материалы для подготовки к ЕГЭ по биологии, схемы и таблицы Проектирование досугового центра
Проектирование досугового центра История русского литературного языка
История русского литературного языка Music in our life
Music in our life Силы, действующие на мотоцикл
Силы, действующие на мотоцикл Новые проекты Санкт-Петербурга
Новые проекты Санкт-Петербурга