Содержание
- 2. § 1. ВВЕДЕНИЕ Линейное алгебраическое уравнение имеет вид: Система m уравнений с n неизвестными: Здесь aij
- 3. Обозначим матрицы: тогда A⋅ Χ = B – запись системы в матричной форме. Решением системы называется
- 4. Решить систему – это, значит, выяснить, совместна ли она, а в случае совместности, найти ее общее
- 5. § 2. МЕТОД ОБРАТНОЙ МАТРИЦЫ Рассмотрим частный случай системы линейных уравнений когда m = n или
- 6. Определитель этой матрицы ∆ называется определителем системы. Если определитель системы не равен нулю, то система называется
- 7. Решение. Представим систему в матричном виде: т.е. в матричной форме система имеет вид A⋅ X =
- 9. Используя формулу X = A−1B, найдем решения системы: т.е. решение системы: x1 = 6, x2 =
- 10. § 3. ФОРМУЛЫ КРАМЕРА Матричное равенство X = A−1B запишем в виде
- 11. Здесь A1ib1 + A2ib2 +…+ Anibn есть разложение определителя по элементам i − го столбца. Тогда
- 13. Скачать презентацию






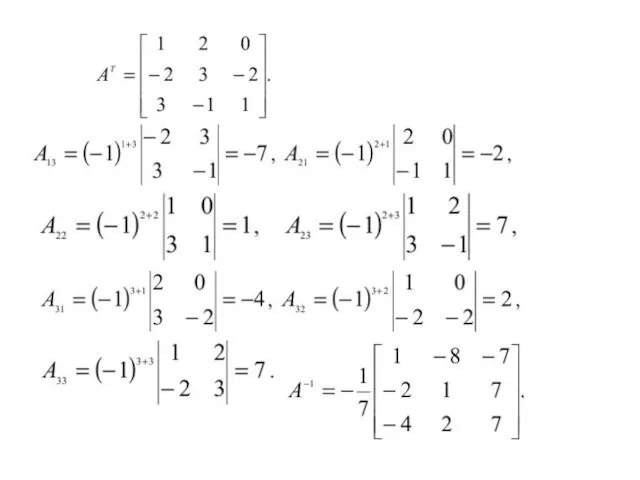



 Правовой режим информации, распространение которой ограничивается или запрещается
Правовой режим информации, распространение которой ограничивается или запрещается Цветы в саду
Цветы в саду Инновационная образовательная программа Теремок для детей от 2 месяцев до 3 лет
Инновационная образовательная программа Теремок для детей от 2 месяцев до 3 лет Теңіз ұңғылары бұрғылау ерекшеліктері
Теңіз ұңғылары бұрғылау ерекшеліктері MY21 exterior plastic tooling delivery and launch
MY21 exterior plastic tooling delivery and launch Детско - родительский проект по теме: Дорога–без приключений
Детско - родительский проект по теме: Дорога–без приключений Токарный станок по дереву. Технология точения конических, фасонных и внутренних поверхностей
Токарный станок по дереву. Технология точения конических, фасонных и внутренних поверхностей Своя игра по математике
Своя игра по математике Проектирование автоматической телефонной станции на железнодорожном транспорте
Проектирование автоматической телефонной станции на железнодорожном транспорте Гласные в корнях с чередованием
Гласные в корнях с чередованием Команда присаивания
Команда присаивания Музей О племени крылатых
Музей О племени крылатых Социально-экономическая обусловленность здоровья населения
Социально-экономическая обусловленность здоровья населения Игра Назови сказку
Игра Назови сказку Дмитрий Сергеевич Мережковский (1865-1941)
Дмитрий Сергеевич Мережковский (1865-1941) Цифровая связь на ЖД транспорте
Цифровая связь на ЖД транспорте Сестринский процесс при заболеваниях детей раннего возраста. Лекция 6
Сестринский процесс при заболеваниях детей раннего возраста. Лекция 6 Традиционные конфессии как основа духовности России
Традиционные конфессии как основа духовности России Презентация История русской письменности немыслима без берестяных грамот
Презентация История русской письменности немыслима без берестяных грамот Родительское собрание
Родительское собрание Женские образы в творчестве В. М. Васнецова
Женские образы в творчестве В. М. Васнецова Концепции современного естествознания
Концепции современного естествознания Lektsia_1_Vvedenie_v_UP
Lektsia_1_Vvedenie_v_UP Острый коронарный синдром
Острый коронарный синдром Строительство школ и детсадов в Пермском крае
Строительство школ и детсадов в Пермском крае Физический и моральный износ промышленных зданий и сооружений. (Лекция 2)
Физический и моральный износ промышленных зданий и сооружений. (Лекция 2)
 Зарождение медицинского страхования в России
Зарождение медицинского страхования в России