Содержание
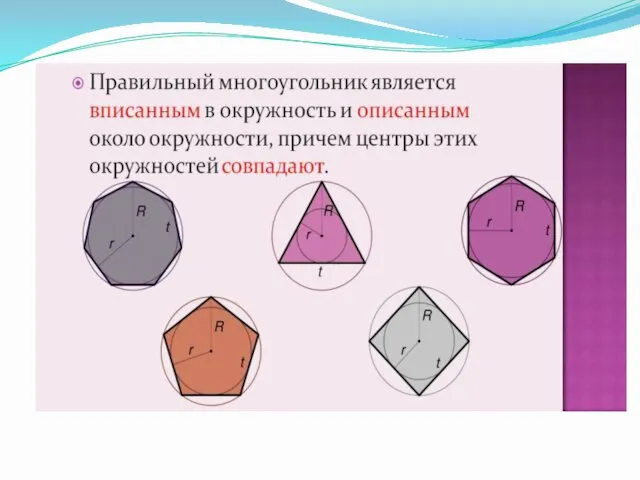
- 2. Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Центром правильного
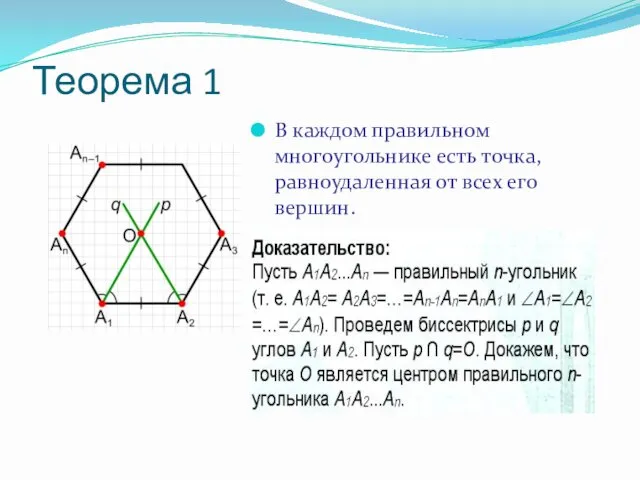
- 3. Теорема 1 В каждом правильном многоугольнике есть точка, равноудаленная от всех его вершин.
- 4. Центр правильного многоугольника Точка, которая равноудалена от всех вершин и от всех сторон правильного многоугольника, является
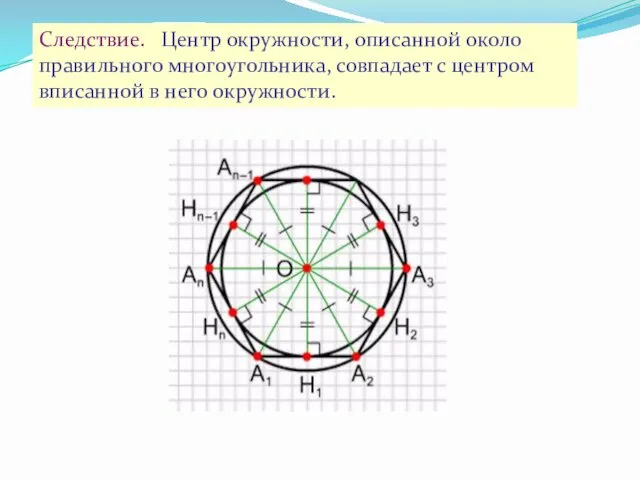
- 5. Следствие. Центр окружности, описанной около правильного многоугольника, совпадает с центром вписанной в него окружности.
- 7. Пример 1 Правильный треугольник (n = 3) Известно, что около любого треугольника АВС, в том числе
- 8. Пример 2 Дан пример окружности, описанной около прямоугольника ABCD. Диагонали прямоугольника пересекаются в точке О, равноудаленной
- 9. Пример 3. Равносторонний треугольник Точка О равноудалена от вершин треугольника: А, В, С, т. к. точка
- 10. Пример 4. Равнобедренная трапеция Следующий пример – равнобедренная трапеция ABCD . Как известно, около такой трапеции
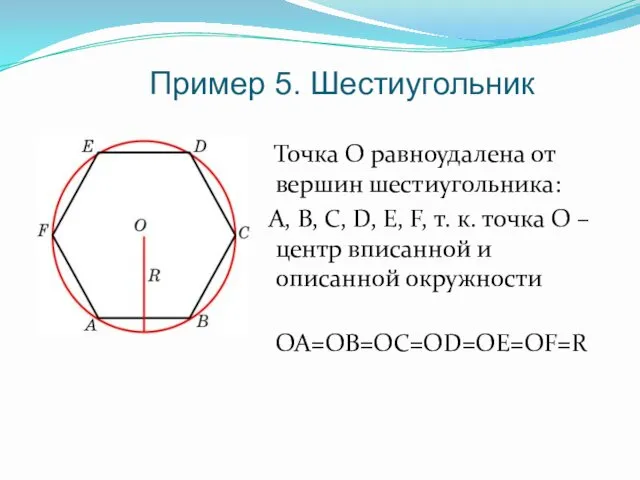
- 11. Пример 5. Шестиугольник Точка О равноудалена от вершин шестиугольника: А, В, С, D, E, F, т.
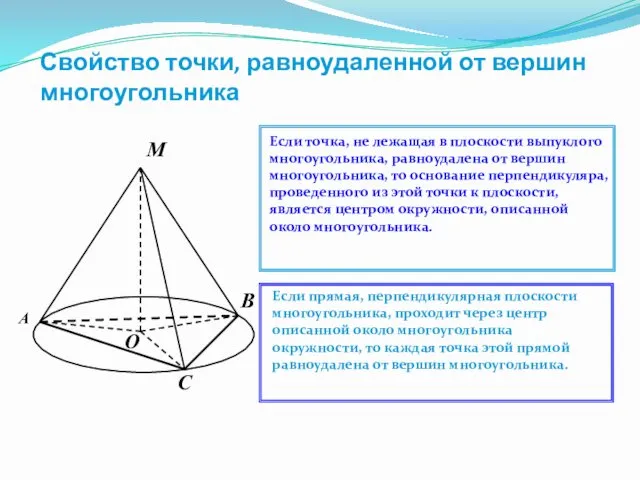
- 12. Свойство точки, равноудаленной от вершины многоугольника Теорема 2. Если через центр окружности, описанной вокруг многоугольника, проведено
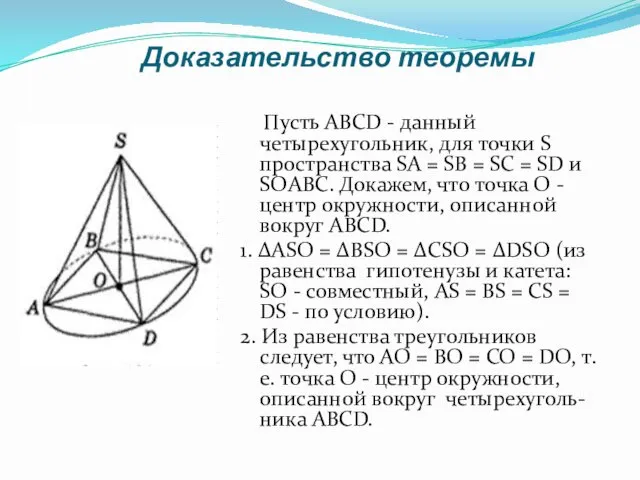
- 13. Доказательство теоремы Пусть ABCD - данный четырехугольник, для точки S пространства SA = SB = SC
- 14. Свойство точки, равноудаленной от вершин многоугольника М О В С А
- 15. Доказательство теоремы Пусть ABCD - четырехугольник, вокруг которого описана окружность с центром в точке О, и
- 16. Свойство точки, равноудаленной от вершины многоугольника Теорема Если некоторая точка равноудалена от вершин многоугольника, то основание
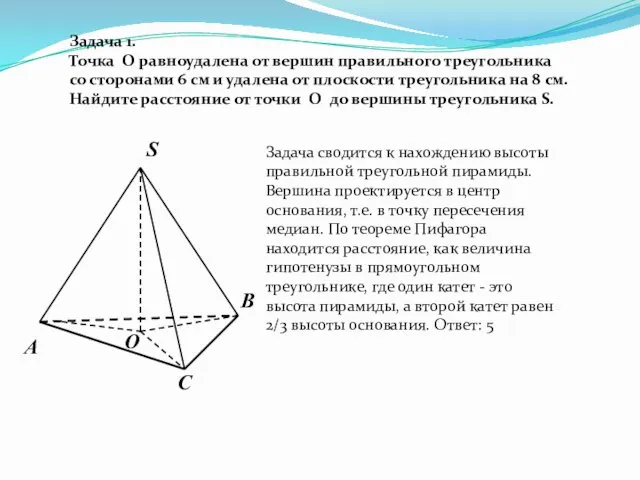
- 17. О С В S А Задача 1. Точка O равноудалена от вершин правильного треугольника со сторонами
- 18. Задача 2 Расстояние от точки А до вершин квадрата равны а. найти расстояние от точки А
- 19. Задача 3 Пусть SO L а - данная прямая, а β - плоскость многоугольника Пусть на
- 20. Решение задачи Рассмотрим ΔA1OS, ΔA2OS, ..., ΔAnOS. Они - прямоугольные, ОА1 = ОА2 = ... =
- 21. Задача 4 Дано: Точка М равноудалена от всех вершин равнобедренного прямоугольного треугольника АВС (угол С=90 градусов).
- 23. Скачать презентацию













 Ультразвуковая диагностика. УЗИ лимфатических узлов
Ультразвуковая диагностика. УЗИ лимфатических узлов Дириг амытаннардан алыр кара эмнер
Дириг амытаннардан алыр кара эмнер Комплекс упражнений для разминки баскетболиста
Комплекс упражнений для разминки баскетболиста Гистиоцитоз. Этиология и патогенез
Гистиоцитоз. Этиология и патогенез Электрические машины и электропривод. Введение
Электрические машины и электропривод. Введение Возможности, преимущества и недостатки автоматической обработки данных
Возможности, преимущества и недостатки автоматической обработки данных Публичная презентация результатов педагогической учителя МБОУ СОШ №74 Зятиковой Светланы Андреевны
Публичная презентация результатов педагогической учителя МБОУ СОШ №74 Зятиковой Светланы Андреевны Мобильное приложение для москвичей и гостей столицы
Мобильное приложение для москвичей и гостей столицы Всемирная компьютерная сеть интернет. Доменная система имен. Протоколы
Всемирная компьютерная сеть интернет. Доменная система имен. Протоколы Технология каменной кладки. Правила разрезки кладки
Технология каменной кладки. Правила разрезки кладки Обобщение опыта работы на тему:Развитие речи детей через использование презентаций по лексическим темам
Обобщение опыта работы на тему:Развитие речи детей через использование презентаций по лексическим темам Прощание с Азбукой
Прощание с Азбукой Синдром Лайелла
Синдром Лайелла Решение тригонометрических уравнений, приводимых к алгебраическим
Решение тригонометрических уравнений, приводимых к алгебраическим Люди милосердия
Люди милосердия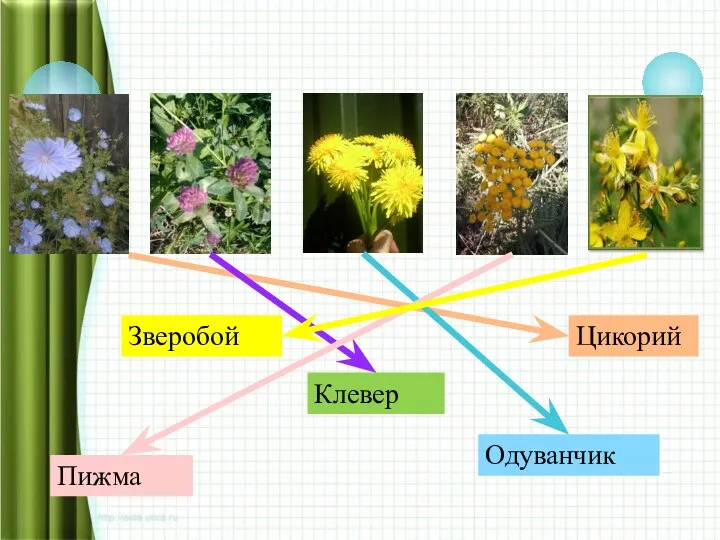 тест по лекарственным растениям
тест по лекарственным растениям Тепловое оборудование. Классификация теплового оборудования
Тепловое оборудование. Классификация теплового оборудования Рак шейки матки
Рак шейки матки Рациональное использование природных ресурсов. (8 класс)
Рациональное использование природных ресурсов. (8 класс) 25 самых необычных животных мира
25 самых необычных животных мира Презентация Создание языковой среды по повторению пройденного материала по татарскому языку
Презентация Создание языковой среды по повторению пройденного материала по татарскому языку Архитектура XVIII века в России
Архитектура XVIII века в России События Октябрьской революции 1917 г. и установление советской власти в Беларуси
События Октябрьской революции 1917 г. и установление советской власти в Беларуси Экологическая политика Японии в годы кризиса
Экологическая политика Японии в годы кризиса Министерство юстиции Российской Федерации. Федеральная служба исполнения наказаний. Федеральная служба судебных приставов
Министерство юстиции Российской Федерации. Федеральная служба исполнения наказаний. Федеральная служба судебных приставов Чудотворцы
Чудотворцы Греция
Греция Что такое настоящий друг
Что такое настоящий друг