Содержание
- 2. Пифагор Самосский Великий учёный Пифагор родился около 570 г.до н.э. на острове Самосе. Отцом Пифагора был
- 3. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 4. Дано: АВС - прямоугольный; а,в - катеты; с – гипотенуза. Доказать: с2=а2+в2. Достроим треугольник до квадрата.
- 5. Проблемный вопрос
- 6. Простейшее доказательство теоремы получается в простейшем случае равно- бедренного прямоугольного треугольни- ка. Вероятно, с него и
- 7. Зная, две стороны прямоугольного треугольника, найдите третью.
- 8. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания»), крупнейшего индийского математика XII в. Бхаскары,
- 9. Решить устно На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17 м,
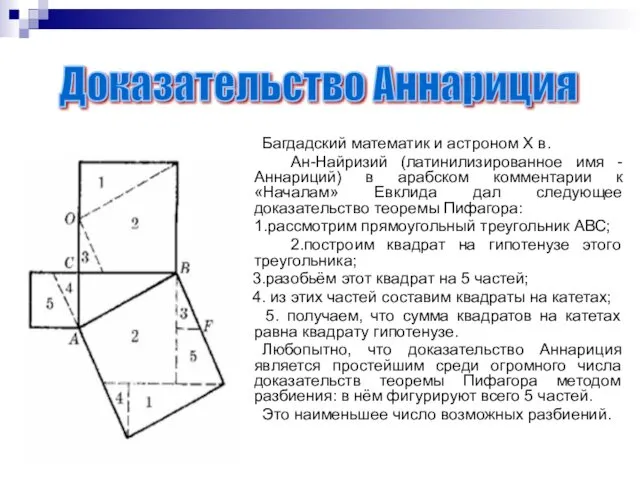
- 10. Доказательство Аннариция Багдадский математик и астроном X в. Ан-Найризий (латинилизированное имя - Аннариций) в арабском комментарии
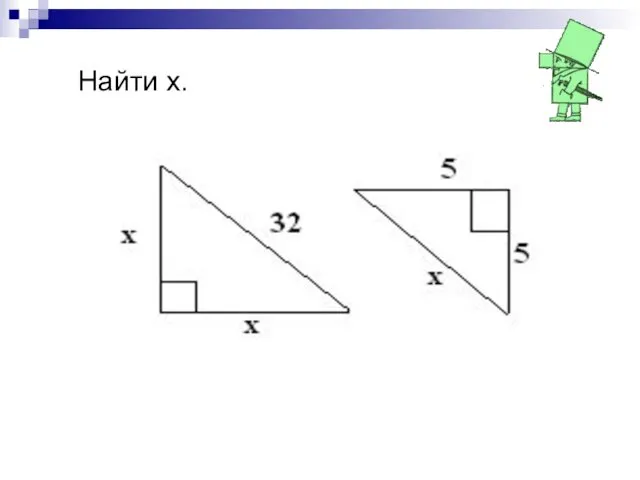
- 11. Найти х.
- 13. Скачать презентацию








 Художественные направления в русской литературе и живописи XVIII-XIX веков
Художественные направления в русской литературе и живописи XVIII-XIX веков Понятие, признаки,структура нормы права
Понятие, признаки,структура нормы права Повторение по теме Текст. 2 класс
Повторение по теме Текст. 2 класс Қант диабеті ауруының алдын алу шаралары тақырыбындағы диплом жұмысы
Қант диабеті ауруының алдын алу шаралары тақырыбындағы диплом жұмысы шаблон Чёрныйдля презентации
шаблон Чёрныйдля презентации Новые форматы офисов
Новые форматы офисов Цветаева Марина Ивановна
Цветаева Марина Ивановна Автомобиль будущего - каким он будет? Технологии будущего. Летающие автомобили
Автомобиль будущего - каким он будет? Технологии будущего. Летающие автомобили Физическое моделирование динамических воздействий на подземные сооружения, основные положения теории подобия
Физическое моделирование динамических воздействий на подземные сооружения, основные положения теории подобия Сестринский уход за недоношенным ребёнком
Сестринский уход за недоношенным ребёнком конспект внеклассного занятия Шоколад - есть или не есть! (согласно требованиям ФГОС ОО)
конспект внеклассного занятия Шоколад - есть или не есть! (согласно требованиям ФГОС ОО) Селекция микроорганизмов
Селекция микроорганизмов Бюджетное право (часть 2)
Бюджетное право (часть 2) Игра-презентация Читаем по слогам
Игра-презентация Читаем по слогам Презентация к уроку географии на тему Безлесные природные зоны России.
Презентация к уроку географии на тему Безлесные природные зоны России. Мой опыт использования разнообразных форм работы с родителями
Мой опыт использования разнообразных форм работы с родителями Имя прилагательное. Имя числительное. Наречие
Имя прилагательное. Имя числительное. Наречие Хобби
Хобби Повсякденне життя українців в 40-50 роках
Повсякденне життя українців в 40-50 роках Хохольский район - без сирот
Хохольский район - без сирот Агрессия и агрессивность. Понятие, виды, рекомендации педагогам
Агрессия и агрессивность. Понятие, виды, рекомендации педагогам Государственные стандарты на выполнение штукатурных и малярных работ
Государственные стандарты на выполнение штукатурных и малярных работ Презентация к сообщению Календари
Презентация к сообщению Календари КУЛЬТУРОВЕДЧЕСКОЕ ОБОГАЩЕНИЕ ИНОЯЗЫЧНОЙ КОММУНИКАТИВНОЙ ПРАКТИКИ СТАРШЕКЛАССНИКОВ
КУЛЬТУРОВЕДЧЕСКОЕ ОБОГАЩЕНИЕ ИНОЯЗЫЧНОЙ КОММУНИКАТИВНОЙ ПРАКТИКИ СТАРШЕКЛАССНИКОВ Крымская война 1853-1856 года
Крымская война 1853-1856 года Выступление на педсовете Системно - деятельностный подход на уроках информатики
Выступление на педсовете Системно - деятельностный подход на уроках информатики 20240107_rabstvo_v_dr_rime
20240107_rabstvo_v_dr_rime Проект Духовно-нравственное воспитание посредством эстетической деятельности
Проект Духовно-нравственное воспитание посредством эстетической деятельности