Содержание
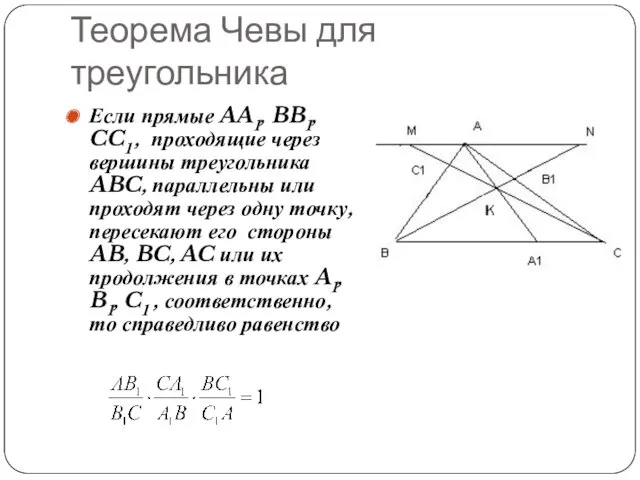
- 2. Теорема Чевы для треугольника Если прямые AA1, BB1, CC1 , проходящие через вершины треугольника ABC, параллельны
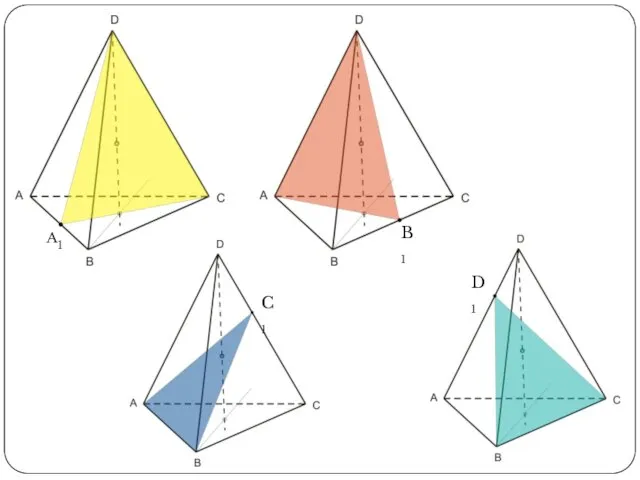
- 3. Обобщение теоремы Чевы Пусть точка M внутри тетраэдра ABCD, точки A1 , B1 , C1, D1
- 4. А1 B1 C1 D1
- 5. Справедливо и обратное: если для точек A1 , B1 , C1, D1 , лежащих на соответствующих
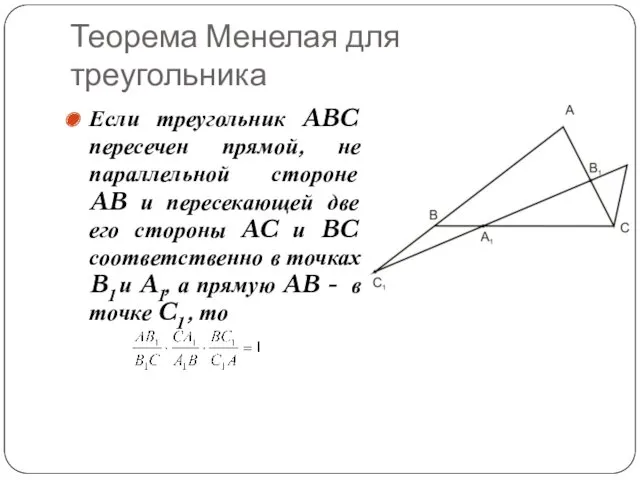
- 6. Теорема Менелая для треугольника Если треугольник ABC пересечен прямой, не параллельной стороне AB и пересекающей две
- 7. Обратная теорема Точки A1, B1, C1 принадлежат прямым BC, CA, AB, соответственно, т.е. лежат на сторонах
- 8. Обобщение теоремы Менелая Если плоскость α пересекает ребра AB, BC, CD, DA тетраэдра ABCD в точках
- 10. Скачать презентацию




 Введение. Основные характеристики сигналов
Введение. Основные характеристики сигналов Монтажные работы СКС. Приемо-сдаточные испытания
Монтажные работы СКС. Приемо-сдаточные испытания Презентация Путешествие В Олимпию(4 класс)
Презентация Путешествие В Олимпию(4 класс) Поливинилхлорид
Поливинилхлорид родной язык 15
родной язык 15 Кома кезіндегі визуальды диагностикасы
Кома кезіндегі визуальды диагностикасы Ericsson RBS 6601
Ericsson RBS 6601 gazeta_bitlerende
gazeta_bitlerende СПЕШИ ТВОРИТЬ ДОБРО.3 декабря - Международный день инвалидов
СПЕШИ ТВОРИТЬ ДОБРО.3 декабря - Международный день инвалидов победа в сердце каждого
победа в сердце каждого Классный час Их именами названы (улицы Красносельского района), посвященный героям Великой Отечественной войны
Классный час Их именами названы (улицы Красносельского района), посвященный героям Великой Отечественной войны Мировая экономика. Международные экономические отношения
Мировая экономика. Международные экономические отношения Силикаты. Лекция 16
Силикаты. Лекция 16 Електрифіковані залізниці. Електропостачання залізниць
Електрифіковані залізниці. Електропостачання залізниць Таблица сложения (1 класс)
Таблица сложения (1 класс) ЖК-мониторы. Принцип действия и свойства
ЖК-мониторы. Принцип действия и свойства Птица из ткани. Традиционная кукла
Птица из ткани. Традиционная кукла Рельеф Африки. 7 класс
Рельеф Африки. 7 класс Правила сервировки и сопровождения вин
Правила сервировки и сопровождения вин Одежда коренных жителей Кузбасса
Одежда коренных жителей Кузбасса Общие закономерности экономической организации общества
Общие закономерности экономической организации общества Приспособительные особенности строения, окраски тела и поведения животных
Приспособительные особенности строения, окраски тела и поведения животных Возникновение ислама. Арабский халифат и его распад. Культурастран Халифата
Возникновение ислама. Арабский халифат и его распад. Культурастран Халифата Элементы и соединения. Узлы Ферм. Лекция 9
Элементы и соединения. Узлы Ферм. Лекция 9 Бытовые электропотребители
Бытовые электропотребители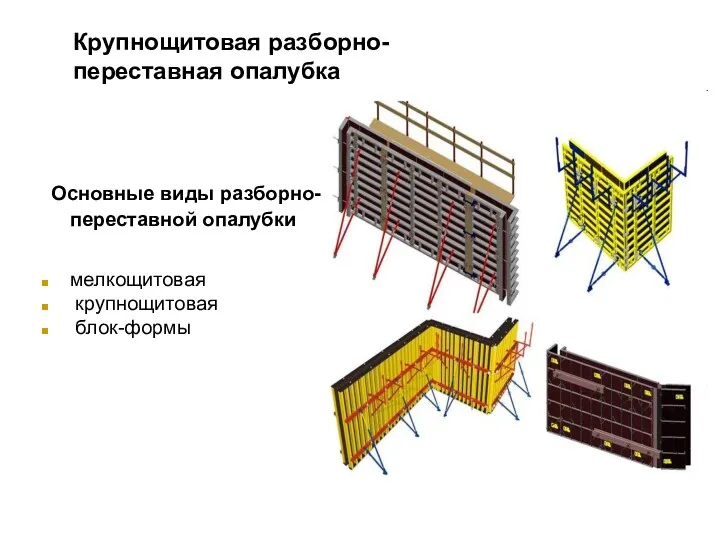 Крупнощитовая разборно-переставная опалубка
Крупнощитовая разборно-переставная опалубка Виды предпринимательской деятельности
Виды предпринимательской деятельности Мировое хозяйство и международное разделение труда
Мировое хозяйство и международное разделение труда