Цифровая обработка сигналов и изображений. Дискретное преобразование Фурье и его свойства презентация
Содержание
- 2. Дискретное преобразование Фурье и его свойства
- 3. Ортогональность сигналов Множество непрерывных функций действительного переменного {Un(t)} = {U0(t), U1(t), …} называется ортогональным на интервале
- 4. Коэффициенты разложения an из указанного соотношения можно определить, если умножить обе его части на Un(t) и
- 5. Для доказательства теоремы Парсеваля возведем обе части соотношения в квадрат: Проинтегрируем обе части: По условию ортогональности:
- 6. Впервые в 1807 году французский математик и физик Жан Батист Жозеф Фурье показал, что любую произвольную
- 7. Коэффициенты {a0, an, bn} можно вычислить с учетом ортогональности множества функций {cos nω0t, sin nω0t} на
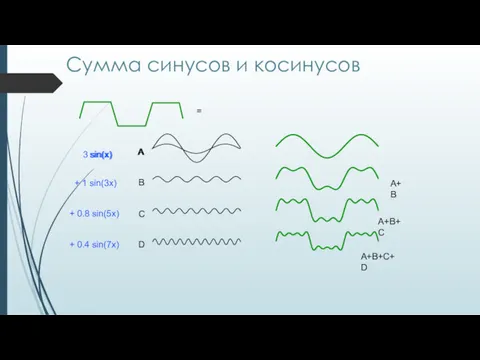
- 8. = Сумма синусов и косинусов
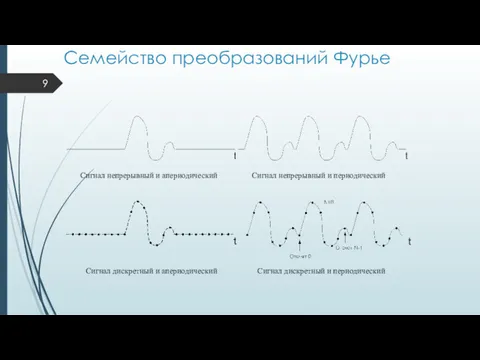
- 9. Семейство преобразований Фурье Cигнал непрерывный и апериодический Cигнал непрерывный и периодический Cигнал дискретный и апериодический Cигнал
- 10. Прямое и обратное непрерывное преобразование Фурье x(t) – исходная функция времени Прямое преобразование Фурье (отображение исходной
- 11. Основная идея дискретного преобразования Фурье Обозначения: X(m) – значение сигнала в момент времени n; – значение
- 12. Таким образом, если {X(m)} означает последовательность X(m) конечных действительных или комплексных чисел, где m = 0,
- 13. Основные свойства ДПФ Теорема линейности Теорема комплексной сопряженности Теорема сдвига Теорема свертки Теорема корреляции
- 14. Основные свойства ДПФ Теорема линейности: ДПФ является линейным, т.е. если то Теорема комплексной сопряженности: если -
- 15. Если и - последовательность действительных чисел, при которых , , а свертка этих последовательностей определяются как
- 16. Если и - последовательность действительных чисел, при которых , , а корреляция этих последовательностей определяются как
- 18. Скачать презентацию













 Презентация о профессии тракторист
Презентация о профессии тракторист Дом из дров и глины по технологии Cordwood
Дом из дров и глины по технологии Cordwood Знаменитые вокалисты Тюмени
Знаменитые вокалисты Тюмени Сказка о язычке
Сказка о язычке Город Глазов в Удмуртской Республике России
Город Глазов в Удмуртской Республике России E-waste
E-waste Великий канон cвятого Андрея Критского, читаемый в четверг пятой седмицы Великого поста
Великий канон cвятого Андрея Критского, читаемый в четверг пятой седмицы Великого поста Вирус иммунодефицита человека
Вирус иммунодефицита человека Памятка контроля по выполнению домашних заданий.
Памятка контроля по выполнению домашних заданий. Агрессия у детей
Агрессия у детей Евразия. Географическое положение (приложение)
Евразия. Географическое положение (приложение) Япония
Япония Влияние Электромагнитного излучения компьютера на память школьников
Влияние Электромагнитного излучения компьютера на память школьников Индивидуальный заказ
Индивидуальный заказ Техническая термодинамика
Техническая термодинамика Презентация: Использование информационно-просветительских форм работы с родителями по правилам дорожного движения
Презентация: Использование информационно-просветительских форм работы с родителями по правилам дорожного движения Фальсификации истории Великой Отечественной войны. Тезисы
Фальсификации истории Великой Отечественной войны. Тезисы Компьютерные сети: типы компьютерных сетей. Топологии компьютерных сетей
Компьютерные сети: типы компьютерных сетей. Топологии компьютерных сетей Оплата по КСГ: преимущества и недостатки
Оплата по КСГ: преимущества и недостатки Активизация интереса к изучению коми языка посредством игры
Активизация интереса к изучению коми языка посредством игры Выбор конструктивных систем
Выбор конструктивных систем Счетчики газа
Счетчики газа История водоснабжения Санкт-Петербурга.
История водоснабжения Санкт-Петербурга. Клинический случай
Клинический случай Первые христиане и их учение
Первые христиане и их учение Электронные ресурсы в учебной деятельности. 10 класс
Электронные ресурсы в учебной деятельности. 10 класс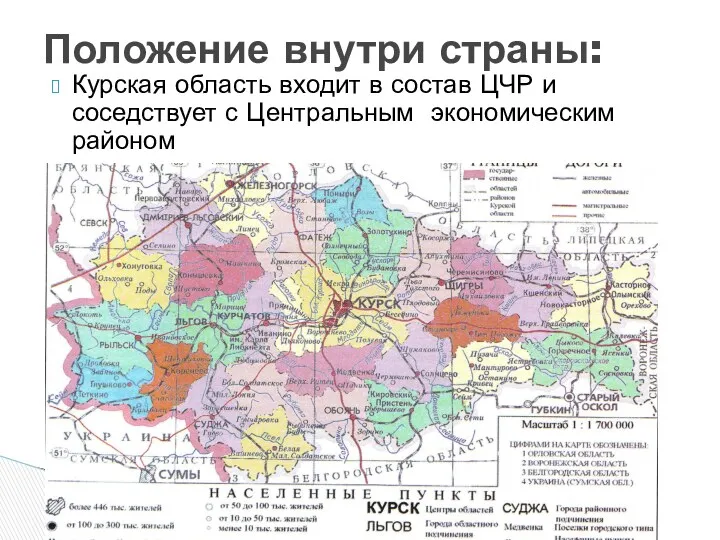 Презентация к уроку Экономико-географическое положение курской области( окончание)
Презентация к уроку Экономико-географическое положение курской области( окончание) Тренажёры для собак для юлагоустройства города и придомовых территорий
Тренажёры для собак для юлагоустройства города и придомовых территорий