Упрощение и оптимизация логических схем. (Лекция 3) презентация

1. Группировка
Применение закона ассоциативности
Применение тождеств – законы отрицания
Пример:
Возможно использование тождества не относящееся к базовым
Пример:

Теорема о непротиворечивости
Пример:
Пусть В·С = Х, а D·E = Y, тогда
Применяя теорему непротиворечивости получаем:

Приведение выражения к каноническому виду с последующем упрощением
1. Выражение записанное в дизъюнктивной форме можно привести к СДНФ путём умножения импликат на множитель типа
2.После раскрытия скобок, члены выражения могут быть так перегруппированы, что в результате получится упрощенное выражение.
Порядок выполнения операций: сначала выполняются операции конъюнкций, а затем дизъюнкций. В сложных логических выражениях для задания порядка выполнения используют скобки.
При необходимости для формирования групп можно ввести повторяющиеся члены.
Пример:

Использование теоремы де Моргана
После инвертирования правых частей
Пример:

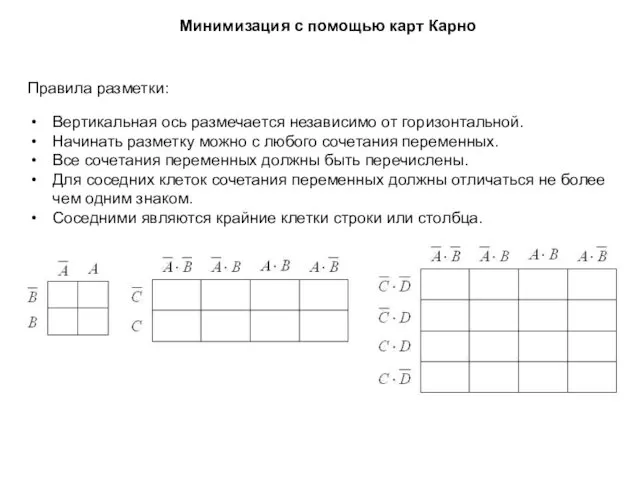
Минимизация с помощью карт Карно
Правила разметки:
Вертикальная ось размечается независимо от горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны быть перечислены.
Для соседних клеток сочетания переменных должны отличаться не более чем одним знаком.
Соседними являются крайние клетки строки или столбца.

Диаграмма Вейча

Правила составления контуров
Контуры должны быть прямоугольными и содержать количество единиц, равное 2n, где n – целое число, т.е. в контуре может быть 1, 2, 4, 8. и т. д. единиц.
Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой.
Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами.

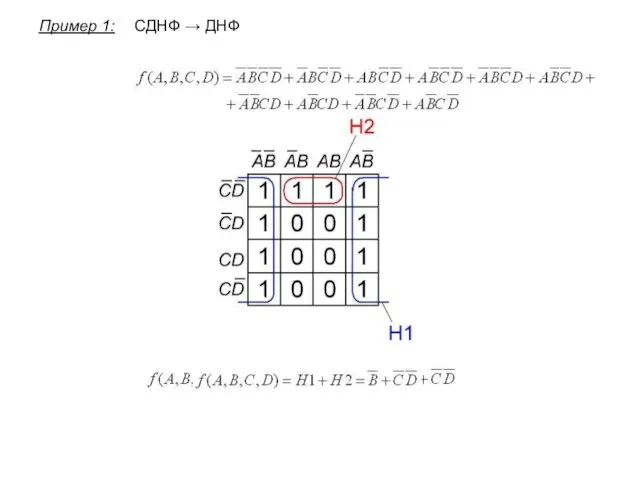
Пример 1:
СДНФ → ДНФ

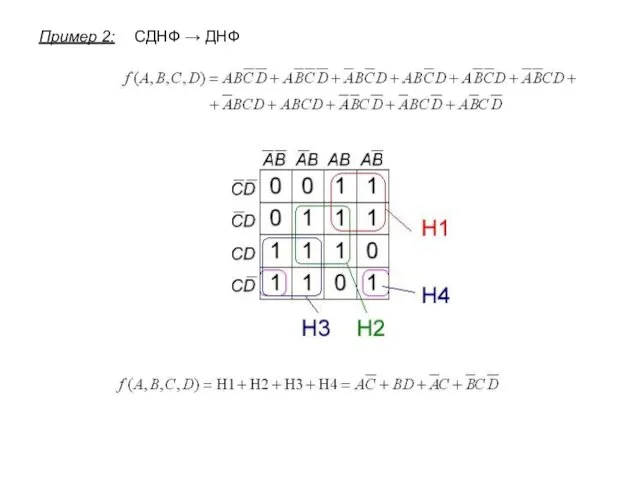
СДНФ → ДНФ
Пример 2:

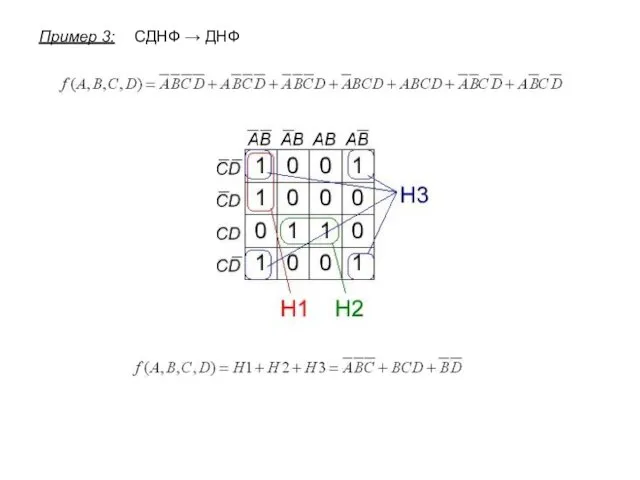
СДНФ → ДНФ
Пример 3:

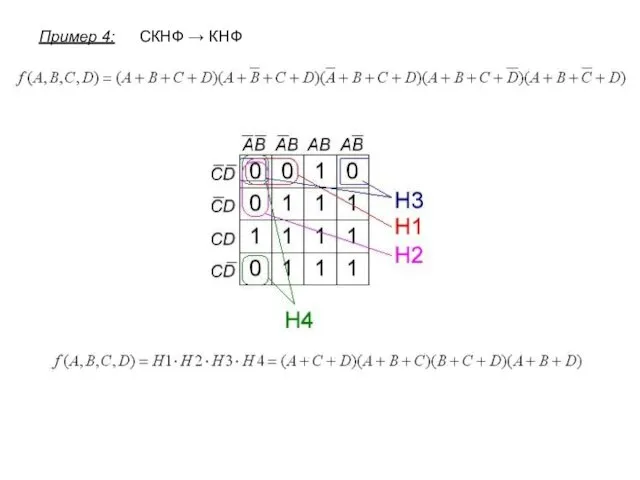
СКНФ → КНФ
Пример 4:

Построение логических схем

При построении логических схем следует придерживаться следующей последовательности:
Этап I. Составление таблицы истинности производится на основе задания содержащего неформальные признаки (определения, «хотелки») допускающие неоднозначную трактовку.
Основная цель – формализация задания.
Результат этапа – составление задания, неоднозначное толкование которого невозможно, то есть составление полностью и однозначно определённой таблицы истинности.
Этап II. Если функция определена не на всех наборах аргументов, то доопределить функцию нулями или единицами, но так, чтобы уменьшить число членов СДНФ прямой функции или её инверсии.
Этап III. По полностью определённой таблице истинности составить СДНФ или несколько СДНФ в зависимости от количества вариантов доопределения.

Этап IV. Минимизировать СДНФ любым доступным методом.
Этап V. Реализовать получившиеся дизъюнктивные формы на логическом базисе заданного семейства элементов.
Этап VI. Оценить двойственный вариант логической схемы с учётом изменения числа входных и выходных инверторов.
Этап VII. Попытаться найти такую декомпозицию функции, чтобы каждый фрагмент полученного разложения зависел от возможно меньшего числа аргументов, чем исходная функция. Попытаться выполнить это различными способами.
Этап VIII. Выбрать из полученных на этапах V, VI, VII вариантов наиболее подходящих с точки зрения поставленной задачи

Оценка качества функциональных схем
Время задержки распространения сигнала – Т
Основные критерии качества функциональной схемы:
Аппаратурные затраты – W

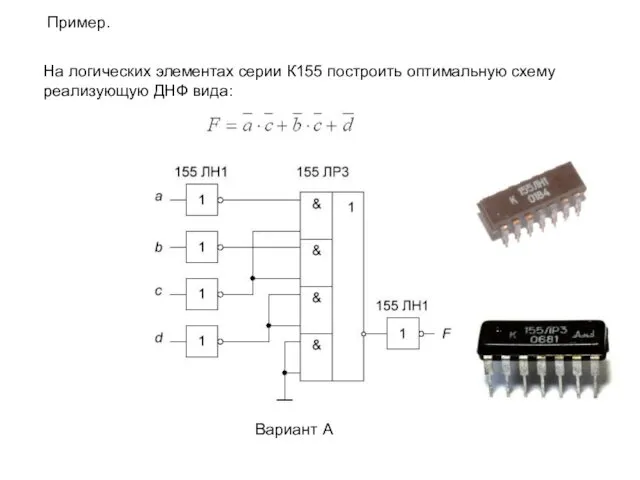
Пример.
На логических элементах серии К155 построить оптимальную схему реализующую ДНФ вида:
Вариант А

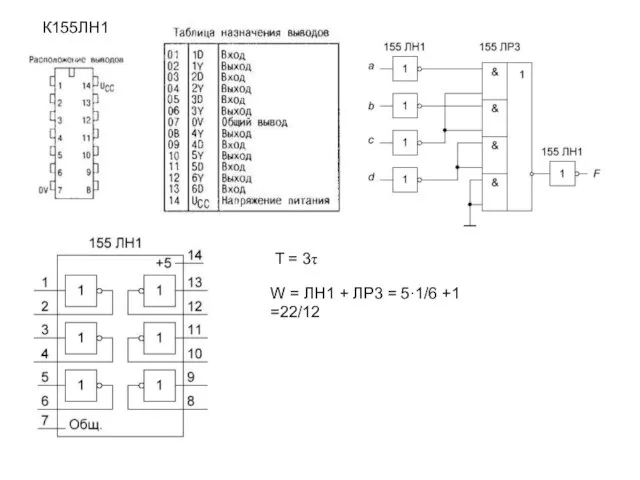
T = 3τ
W = ЛН1 + ЛР3 = 5·1/6 +1 =22/12
К155ЛН1

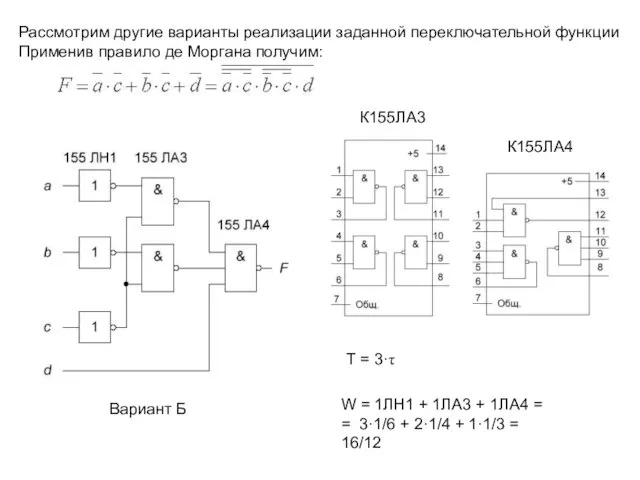
Рассмотрим другие варианты реализации заданной переключательной функции
Применив правило де Моргана получим:
К155ЛА3
К155ЛА4
Вариант Б
W = 1ЛН1 + 1ЛА3 + 1ЛА4 =
= 3·1/6 + 2·1/4 + 1·1/3 = 16/12
Т = 3·τ

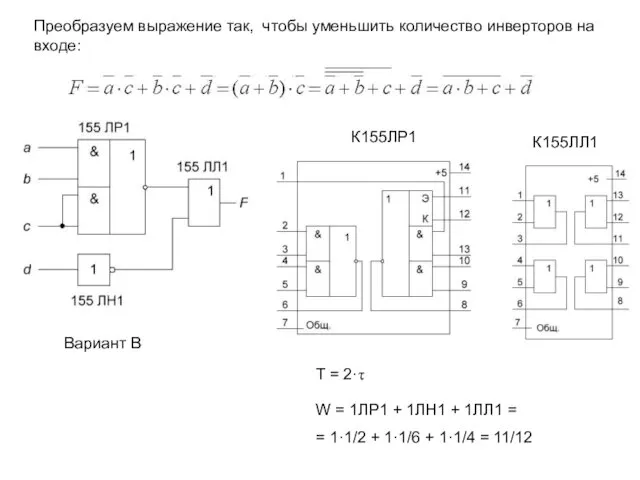
Преобразуем выражение так, чтобы уменьшить количество инверторов на входе:
К155ЛР1
К155ЛЛ1
Вариант В
T = 2·τ
W = 1ЛР1 + 1ЛН1 + 1ЛЛ1 =
= 1·1/2 + 1·1/6 + 1·1/4 = 11/12

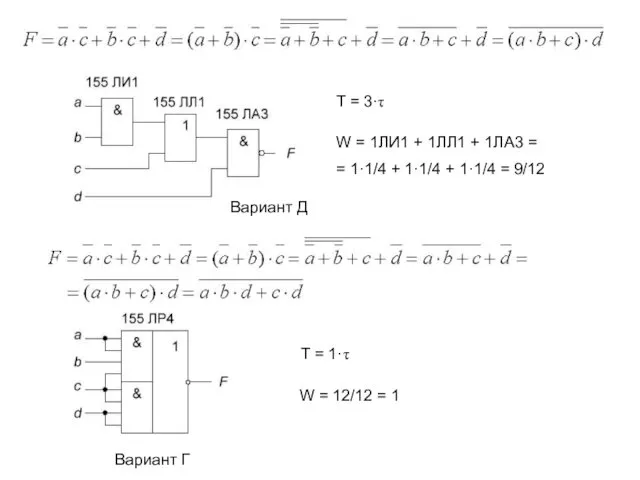
T = 3·τ
W = 1ЛИ1 + 1ЛЛ1 + 1ЛА3 =
= 1·1/4 + 1·1/4 + 1·1/4 = 9/12
T = 1·τ
W = 12/12 = 1
Вариант Д
Вариант Г

Говорят, что х доминирует над х* “по Парето”, если х не хуже х* по всем критериям и хотя бы по одному критерию превосходит х*. В таком случае в выборе х* нет смысла, так как х по всем параметрам не уступает, а по каким-то и превосходит х.
Если рассматривать всего два критерия, то на рисунке 1 показана область пространства, доминируемая решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А.
Рисунок 1 – Доминируемые решения
Решением задачи оптимизации, с несколькими критериями, является множество Парето.
Элемент х* ∈ {X} – называется “оптимальным по Парето”, если не существует такого х ∈ {X} , который будет “лучше” х*.

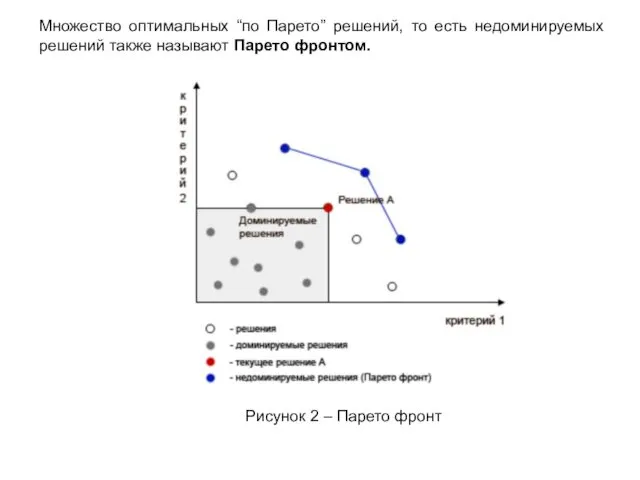
Множество оптимальных “по Парето” решений, то есть недоминируемых решений также называют Парето фронтом.
Рисунок 2 – Парето фронт