Содержание
- 2. В 1924 г. французский физик Луи де Бройль предположил, что любая частица, в том числе и
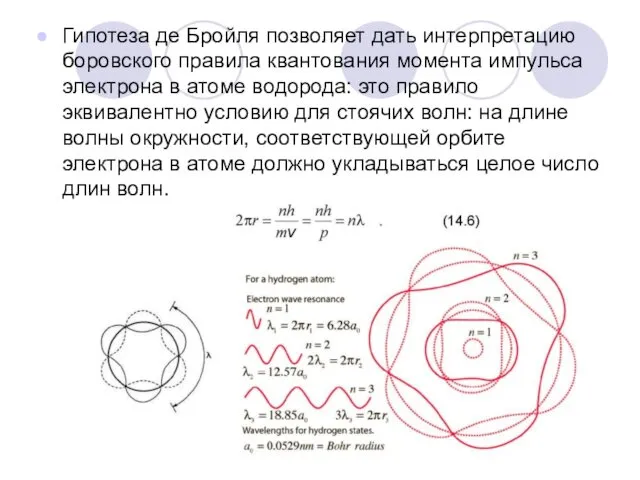
- 3. Гипотеза де Бройля позволяет дать интерпретацию боровского правила квантования момента импульса электрона в атоме водорода: это
- 4. Можно ввести понятие волнового числа, то есть числа волн, укладывающихся на 2 см = 1,054·10-34 Дж
- 5. Кинетическая энергия свободного электрона =9,1 10-31 кг – масса свободного электрона
- 6. В 1926 г. австрийский физик Эрвин Шрёдингер вывел уравнение для волн де Бройля. Волна, связанная с
- 7. Уравнение Шрерингера Э́рвин Ру́дольф Йо́зеф Алекса́ндр Шрёдингер (нем. Erwin Rudolf Josef Alexander Schrödinger 12 12 08
- 8. Квантовые операторы − символические изображения математических операций преобразования величин в квантовой теории. В квантовой механике постулируется,
- 9. Например: оператор может означать дифференцирование по какой-либо переменной
- 10. Примеры некоторых операторов Оператор координаты равен самой координате x, т.е. сводится к умножению на эту переменную:
- 11. Энергия частицы массой имеет две составляющие – кинетическую и потенциальную: В этом случае , где −
- 12. Свободная частица массы m0: - оператор Лапласа Примеры некоторых гамильтонианов
- 13. Примеры некоторых гамильтонианов Частица в одномерной потенциальной яме U(x), 0
- 14. Кинетическая энергия Если заменить в правой части уравнения величину импульса на так называемый оператор импульса, –
- 15. операторы проекций импульсов
- 16. уравнения для собственных функций и собственных значений операторов проекций импульсов
- 17. Решением первого уравнения системы является волновая функция где - произвольная функция (y,z) - уравнение Шредингера для
- 18. Уравнение Шредингера для свободной частицы Решения уравнения Шрёдингера существуют только для волновых функций, характеризуемых набором целых
- 19. Уравнение Шредингера для свободной частицы В стационарном случае Шредингер заметил, что при определенных условиях решение его
- 21. Учитывая потенциальную энергию электрона Это уравнение в частных производных имеет множество решений. В каждой конкретной задаче
- 23. В любой момент времени t, состояние квантовой частицы задается двумя величинами: координатами (радиусом-вектором) и импульсом: –
- 24. Волновая функция Это – комплексная синусоида.
- 25. Решения в виде стоячей волны зависят от времени благодаря множителю , причем возможные значения частоты образуют
- 26. Волновая функция Если нам известна волновая функция (5), то из нее можно получить энергию, продифференцировав ее
- 27. Волновая функция
- 28. Как определить саму волновую функцию? в соответствии с соотношением неопределенностей немецкого физика Вернера Гейзенберга, выведенного им
- 29. Ве́рнер Карл Ге́йзенберг (нем. Werner Karl Heisenberg; 5 5 12 19015 12 1901 — 1 5
- 32. Максимум, что можно сделать – это определить три координаты или три компоненты импульса, а затем из
- 33. Так что такое волновая функция? В 1926 г. немецкий физик Макс Борн предложил, что волновая функция
- 34. Макс Борн Макс Борн (нем. Max Born; 11; 1112 1882; 1112 1882 - 5 ; 1112
- 35. Волновая функция Шредингеровская волновая функция (амплитуда волны де Бройля) определяет вероятность нахождения частицы в данной точке
- 36. Вероятность обнаружить данную частицу в объеме dV здесь – комплексно-сопряженная с функцией . Согласно Постулата №1
- 38. Для свободной частицы =0 Таким образом, для свободной частицы общее решение представляется в виде двух монохроматических
- 39. Если взять волну де Бройля, идущую в сторону положительных значений оси Х, то и значит, плотность
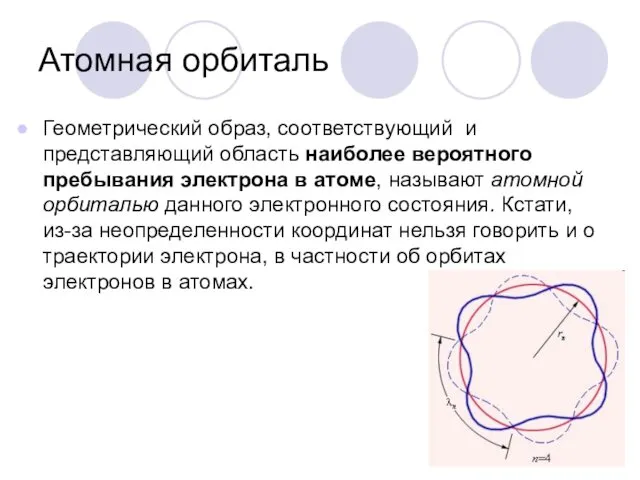
- 40. Атомная орбиталь Геометрический образ, соответствующий и представляющий область наиболее вероятного пребывания электрона в атоме, называют атомной
- 41. При условии стационарности поля внешних сил ( ) волновую функцию можно представить в следующем виде: ,
- 42. После разделения переменных можно получить два уравнения для временной и координатной частей функции соответственно:
- 43. Решение уравнения с точностью до множителя С будет иметь во всех случаях один и тот же
- 44. Решение уравнение Шредингера частицы, находящейся в потенциальной яме
- 45. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Вводя обозначение В=0
- 46. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Заметим, что условие соответствует образованию в области стоячей
- 48. Решение уравнение Шредингера частицы, находящейся в потенциальной яме где n=1, 2, 3…
- 49. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Случай п=0 следует отбросить, так как при этом
- 50. Решение уравнение Шредингера частицы, находящейся в потенциальной яме
- 51. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Как энергия состояния, так и разность энергий соседних
- 52. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Каждому значению соответствует собственная волновая функция
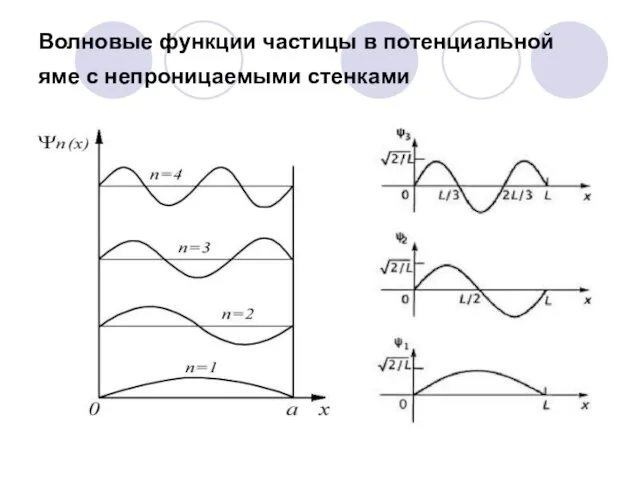
- 53. Волновые функции частицы в потенциальной яме с непроницаемыми стенками
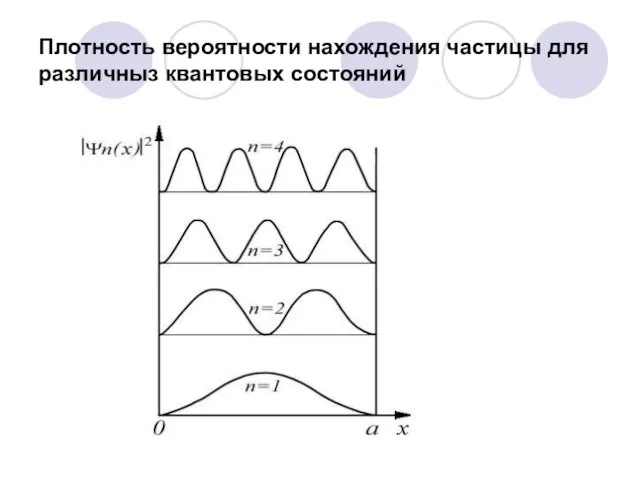
- 54. Плотность вероятности нахождения частицы для различныз квантовых состояний
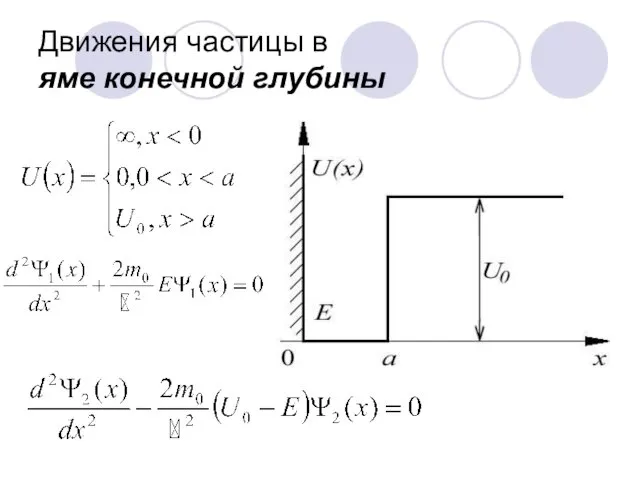
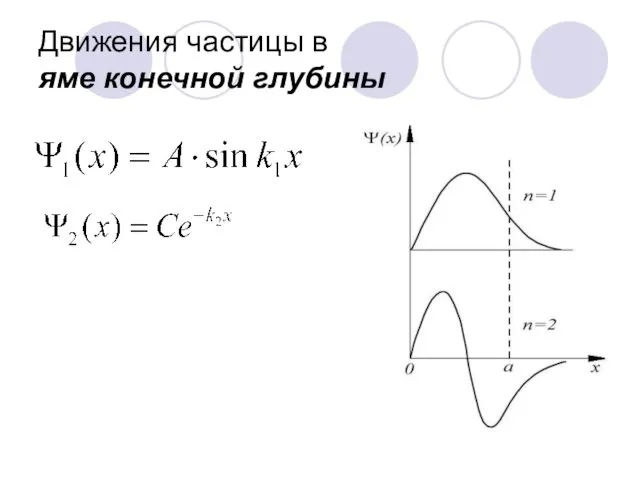
- 55. Движения частицы в яме конечной глубины
- 56. Движения частицы в яме конечной глубины
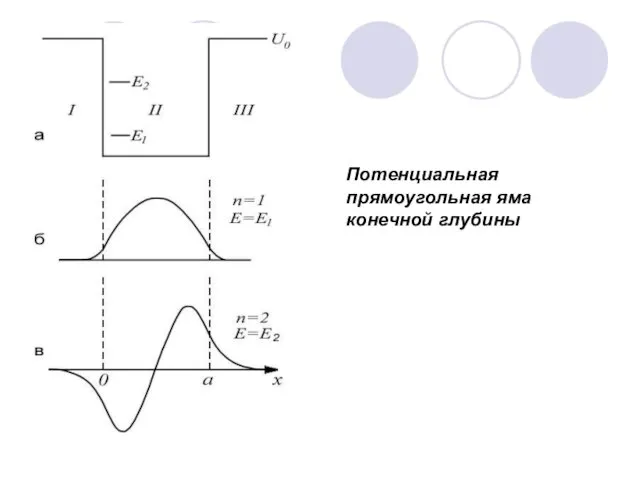
- 57. Потенциальная прямоугольная яма конечной глубины
- 58. Потенциальная прямоугольная яма конечной глубины
- 59. Туннельный эффект Как было показано, решение уравнения Шредингера для свободной частицы (U=0) дает одинаковую плотность вероятности
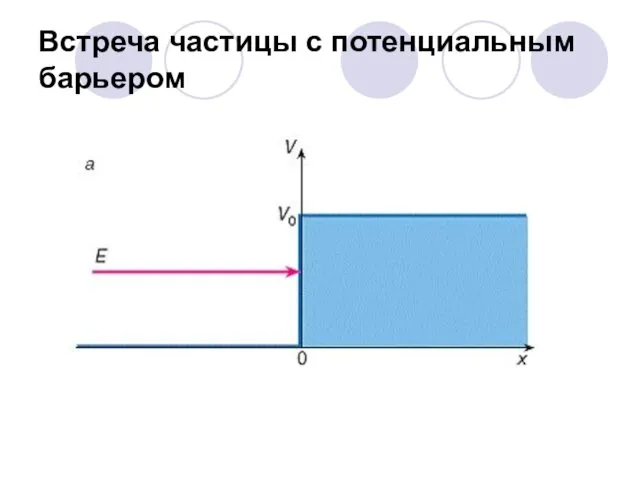
- 60. Встреча частицы с потенциальным барьером
- 61. Встреча частицы с потенциальным барьером В рамках классической механики априорно ясно, что тело имеющее полную энергию
- 62. Встреча частицы с потенциальным барьером Туннельный эффект является принципиально квантово-механическим эффектом, не имеющим аналогов в классической
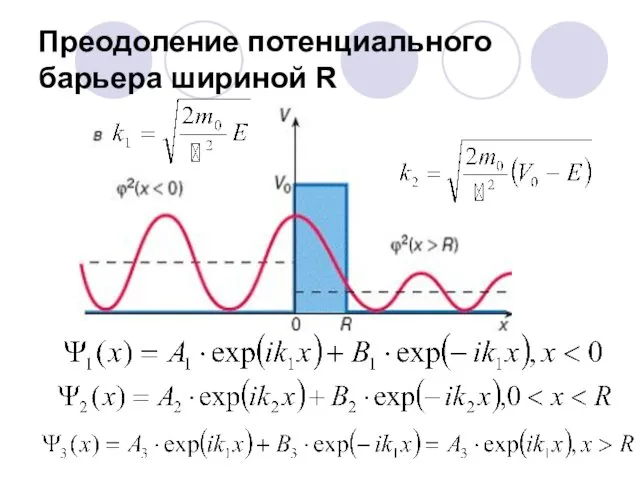
- 63. Преодоление потенциального барьера шириной R
- 64. Преодоление потенциального барьера шириной R Отношение квадратов модулей амплитуд отраженной и падающей волн определяет коэффициент отражения
- 65. Коэффициент прохождения D (коэффициент прозрачности), определяющий часть потока частиц, прошедшего сквозь барьер, связан с коэффициентом отражения:
- 66. Встреча частицы с потенциальным барьером Рассмотрение случая высокого потенциального барьера ( ) проводится аналогично, но теперь
- 67. Полагая В2=0 (отражением от второй границы барьера можно пренебречь при условии достаточно высокого и широкого потенциального
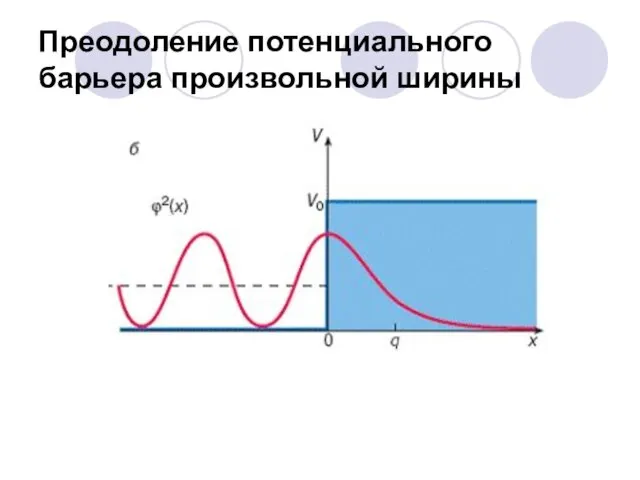
- 68. Преодоление потенциального барьера произвольной ширины
- 69. Можно показать, что для высокого потенциального барьера любой формы коэффициент прозрачности , то есть имеется вероятность
- 70. Вероятность туннелирования уменьшается с ростом ширины барьера, его высоты (точнее, разности ) и с увеличением массы
- 71. Основы теории туннельных переходов заложены работами советских ученых Л.И. Мандельштама и М.А. Леонтовича в 1928 г.
- 72. Квантовый осциллятор Известно, что гармонический осциллятор, то есть система, совершающая гармонические колебания с круговой частотой ,
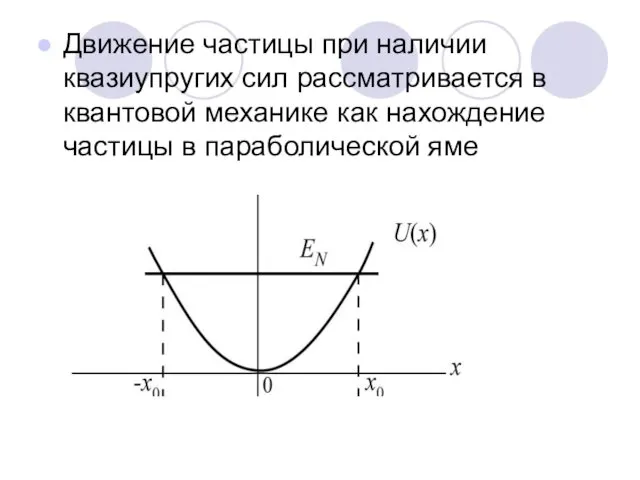
- 73. Движение частицы при наличии квазиупругих сил рассматривается в квантовой механике как нахождение частицы в параболической яме
- 74. Гамильтониан для потенциальной энергии примет вид:
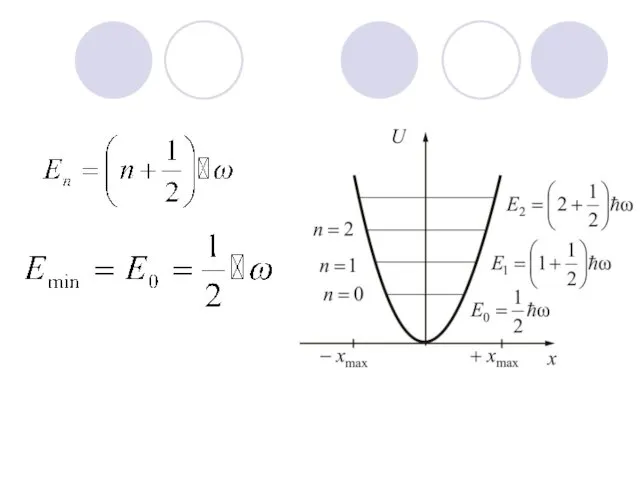
- 75. Вводя величины где n=0, 1, 2, 3…
- 77. Отметим, что уровни гармонического квантового осциллятора, в отличие от случая прямоугольной потенциальной ямы, расположены на равных
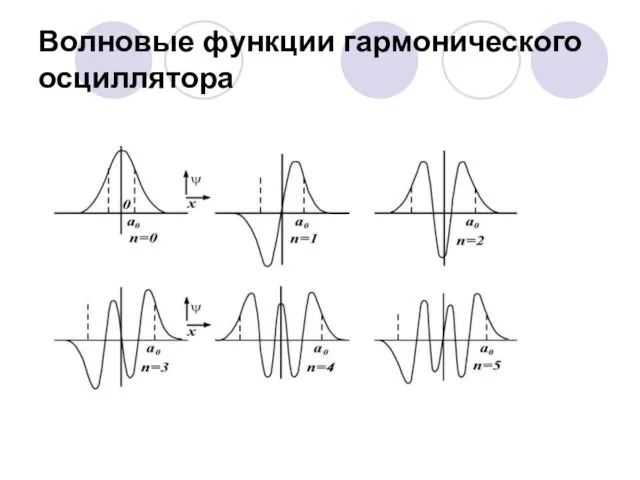
- 78. Приведем вид волновых функций для первых трех энергетических уровней гармонического осциллятора: n=0, , n=1, n=2,
- 79. Волновые функции гармонического осциллятора
- 80. Отметим, что вне классической области волновые функции отличны от нуля, что свидетельствует о том, что квантовый
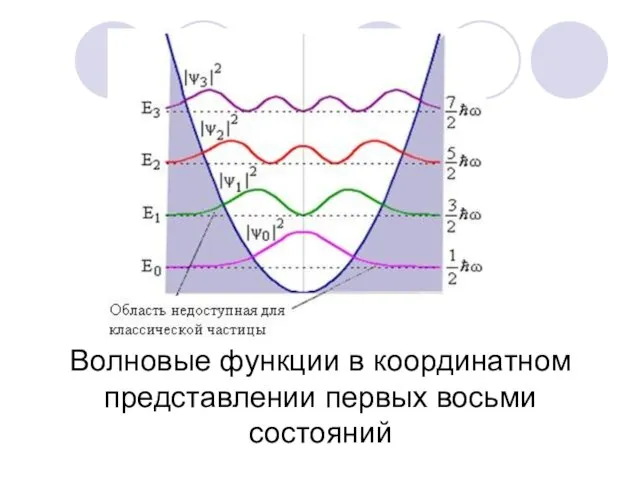
- 81. Волновые функции в координатном представлении первых восьми состояний
- 82. Сколько электронов может находиться на одной орбите? Вольфганг Паули в 1925 г. сформулировал принцип запрета: на
- 84. В 1940 г. тот же Паули выдвинул теорему, согласно которой для частиц с полуцелым спином (фермионов)
- 85. Свое название – фермионы, частицы с полуцелым спином (электроны, дырки) получили по имени итальянского физика Энрико
- 86. Частицы с целым спином (включая нуль) – бозоны, по имени индийского ученого Шатьендраната Бозе.
- 88. Скачать презентацию







































































 Диаграммы деятельности
Диаграммы деятельности Интегрированный урок обобщающего повторения Путешествуем по миру (география + математика)
Интегрированный урок обобщающего повторения Путешествуем по миру (география + математика) Концепция общества и человека в драматических произведениях М. Горького
Концепция общества и человека в драматических произведениях М. Горького Проектирование многоэтажных жилых зданий массовой застройки для Крайнего Севера
Проектирование многоэтажных жилых зданий массовой застройки для Крайнего Севера Лекция №3. Функции промышленных СУБД
Лекция №3. Функции промышленных СУБД Обыкновенные дроби. Игра Счастливый случай
Обыкновенные дроби. Игра Счастливый случай Разработка алгоритма повышения помехоустойчивости канала связи с использованием технологии MIMO
Разработка алгоритма повышения помехоустойчивости канала связи с использованием технологии MIMO Педагогический опыт
Педагогический опыт Презентация системы работы по профилактике оптической дисграфии
Презентация системы работы по профилактике оптической дисграфии Внутрилабораторный контроль качества лабораторных исследований в УЗ
Внутрилабораторный контроль качества лабораторных исследований в УЗ Мой педагогический опыт
Мой педагогический опыт Технологическая оснастка обсадных колонн. Лекция 8
Технологическая оснастка обсадных колонн. Лекция 8 Сбор макулатуры
Сбор макулатуры Христианский антисемитизм
Христианский антисемитизм Кроссворд Насекомые; 1-2 класс
Кроссворд Насекомые; 1-2 класс Игра Вокгуг света
Игра Вокгуг света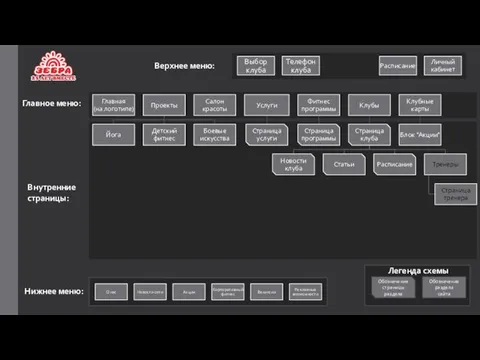 Структура сайта фитнес-клуба
Структура сайта фитнес-клуба презентация по теме: Физические явления в химии
презентация по теме: Физические явления в химии Новые приоритеты государственной образовательной политики в ХХI веке, в сфере исторического и обществоведческого образования
Новые приоритеты государственной образовательной политики в ХХI веке, в сфере исторического и обществоведческого образования Статистические методы обработки информации
Статистические методы обработки информации The Cry of a Wounded Heart
The Cry of a Wounded Heart Острый аппендицит
Острый аппендицит Терминальные состояния. Сердечно-легочная реанимация. Шок
Терминальные состояния. Сердечно-легочная реанимация. Шок Дифференциация обучения с использованием ИКТ для повышения качества обучения.
Дифференциация обучения с использованием ИКТ для повышения качества обучения. Оригами из бумаги. Аппликация Аквариум 1 класс
Оригами из бумаги. Аппликация Аквариум 1 класс Путешествие финикийских мореплавателей
Путешествие финикийских мореплавателей Бальные танцы. Румба.
Бальные танцы. Румба. Тест по химии (8 класс) по теме Генетическая связь классов неорганических соединений для системы тестирования PROClass
Тест по химии (8 класс) по теме Генетическая связь классов неорганических соединений для системы тестирования PROClass