Содержание
- 2. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 3. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 4. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 5. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 6. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 7. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 8. Если α будет произвольным комплексным числом, то множество сигналов образует Комплексное Линейное Пространство Сигналов С. Элементы
- 9. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 10. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 11. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 12. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 13. Общая теория связи Лекция №3 Если S2(t) = 0 то имеем систему передачи с пассивной паузой
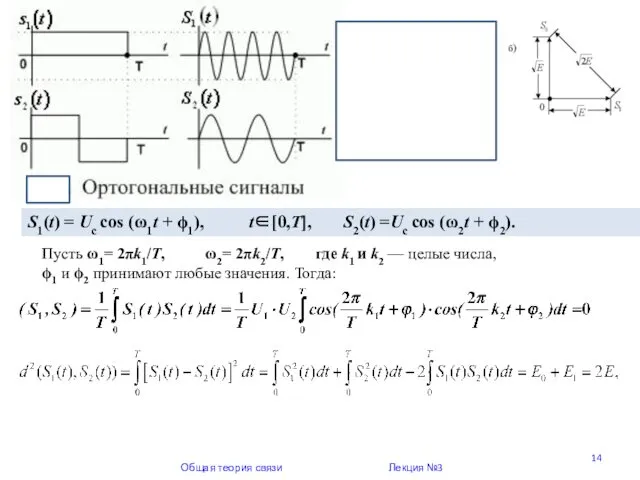
- 14. Общая теория связи Лекция №3 S1(t) = Uc cos (ω1t + ϕ1), t∈[0,T], S2(t) =Uc cos
- 15. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 16. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 17. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 18. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
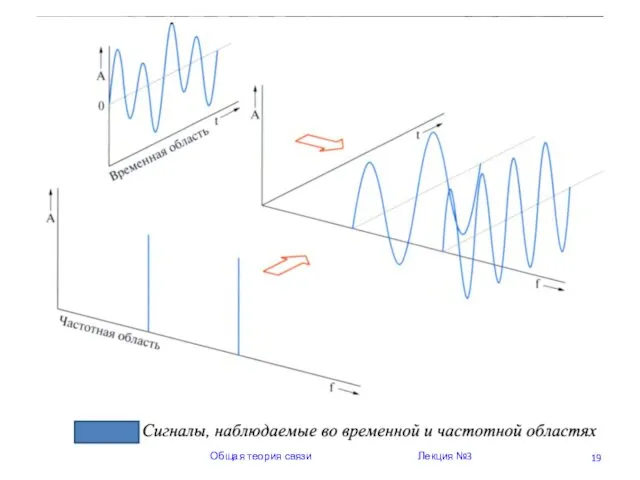
- 19. Общая теория связи Лекция №3
- 20. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 21. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
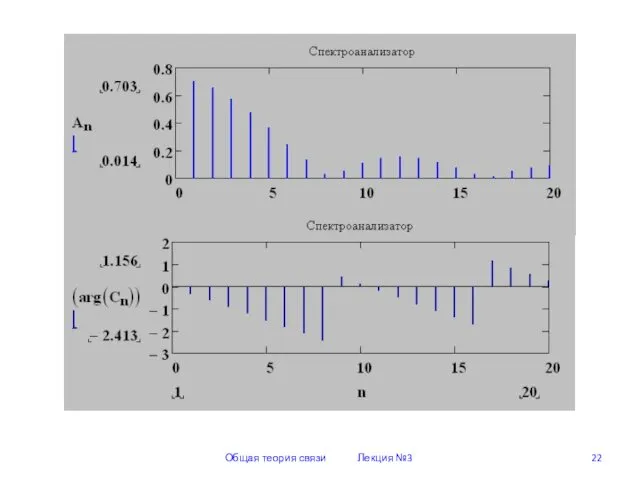
- 22. Общая теория связи Лекция №3
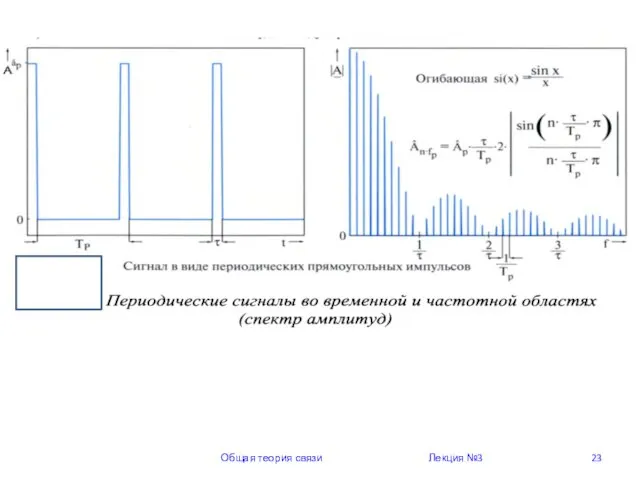
- 23. Общая теория связи Лекция №3
- 24. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 25. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 26. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 27. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
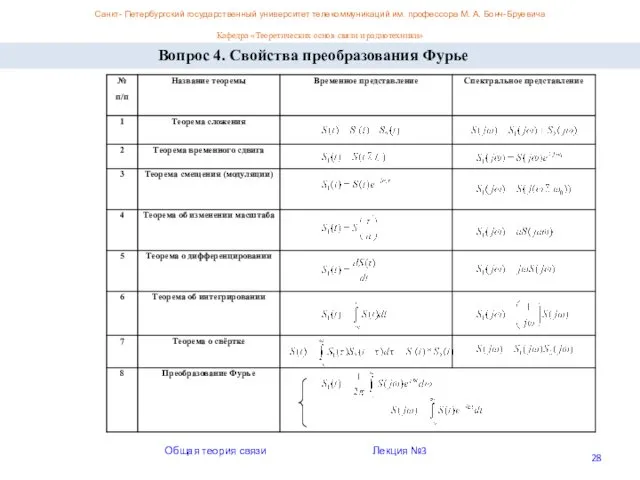
- 28. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники»
- 30. Скачать презентацию




















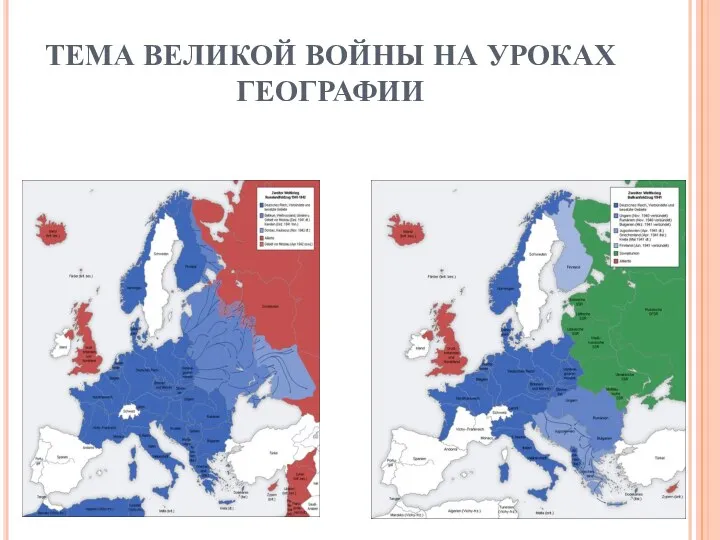 Тема Великой Войны на уроках географии
Тема Великой Войны на уроках географии Технологии машиностроения. Базы в машиностроении. Классификация баз
Технологии машиностроения. Базы в машиностроении. Классификация баз Оценка образовательных результатов
Оценка образовательных результатов Обеспечение личной безопасности на водоемах в различное время года
Обеспечение личной безопасности на водоемах в различное время года Обособленные уточняющие члены предложения. Знаки препинания при них
Обособленные уточняющие члены предложения. Знаки препинания при них Классный час Поговорим о дружбе
Классный час Поговорим о дружбе Компания ООО Русский Базальт. Производство базальтового непрерывного волокна и продукции на его основе
Компания ООО Русский Базальт. Производство базальтового непрерывного волокна и продукции на его основе 20230916_risuem_po_koordinatam
20230916_risuem_po_koordinatam Роль особи Жана Кальвіна в добу реформації
Роль особи Жана Кальвіна в добу реформації Проект А у нас огород на окне
Проект А у нас огород на окне Укрепление грунтов оснований
Укрепление грунтов оснований презентация Простые вещества - неметаллы
презентация Простые вещества - неметаллы Вам, нашим мамам, самым любимым и самым желанным!
Вам, нашим мамам, самым любимым и самым желанным! Экологические сообщества
Экологические сообщества проверка - закрепление по теме Общие сведения о галогеноводородах
проверка - закрепление по теме Общие сведения о галогеноводородах Геологические процессы в недрах Земли
Геологические процессы в недрах Земли Профессия воспитатель
Профессия воспитатель Архитектурные шрифты. Правила построения
Архитектурные шрифты. Правила построения Методическая разработка урока благотворительности Дорогой доброты,
Методическая разработка урока благотворительности Дорогой доброты, Санитарно-гигиенические условия обеспечения учебного процесса
Санитарно-гигиенические условия обеспечения учебного процесса Предохранители. Виды предохранителей
Предохранители. Виды предохранителей Диверсификация производств и интеграция строительных организаций
Диверсификация производств и интеграция строительных организаций Синэкология (экология сообществ)
Синэкология (экология сообществ) Конструкт урока Ъ и Ь
Конструкт урока Ъ и Ь Информационная культура в непрерывном образовании личности. Комфортная информационная среда. (Тема 1)
Информационная культура в непрерывном образовании личности. Комфортная информационная среда. (Тема 1) Tesla Motors MODEL S. Электромобиль
Tesla Motors MODEL S. Электромобиль Презентация хлеб
Презентация хлеб Религия, как форма общественного сознания
Религия, как форма общественного сознания