Содержание
- 2. ТЕОРЕМА ЭЙЛЕРА Из приведенной таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В
- 3. Л. ЭЙЛЕР Леонард Эйлер (1707-1783) - один из величайших математиков мира, работы которого оказали решающее влияние
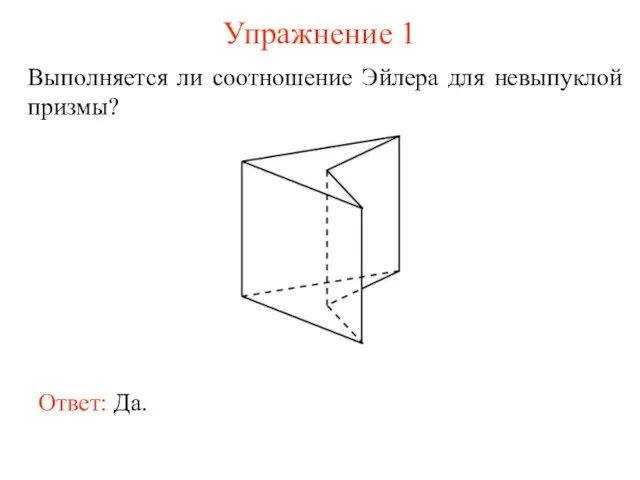
- 4. Упражнение 1 Выполняется ли соотношение Эйлера для невыпуклой призмы? Ответ: Да.
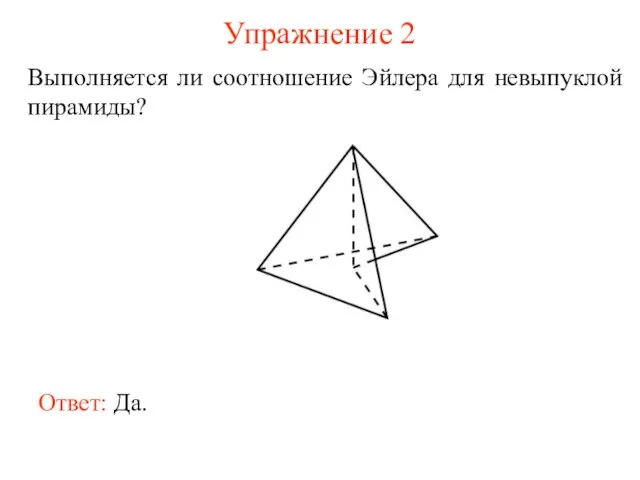
- 5. Упражнение 2 Выполняется ли соотношение Эйлера для невыпуклой пирамиды? Ответ: Да.
- 6. Упражнение 3 Посчитайте число вершин (В), ребер (Р) и граней (Г) у многогранников, изображенных на рисунке.
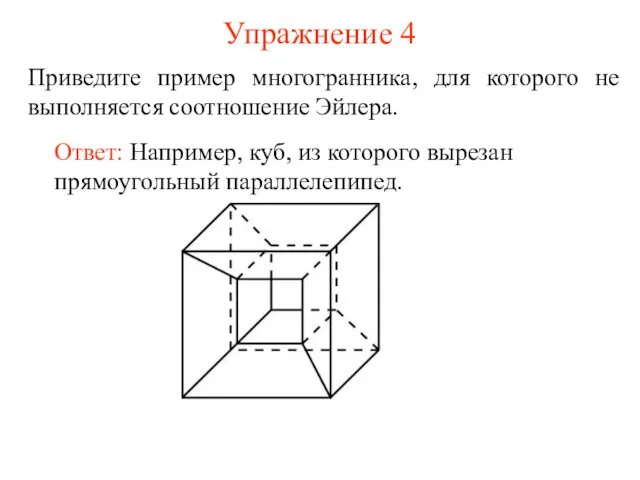
- 7. Упражнение 4 Приведите пример многогранника, для которого не выполняется соотношение Эйлера.
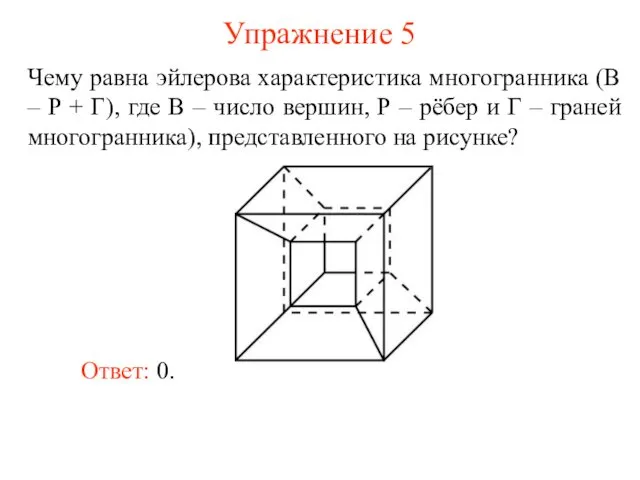
- 8. Упражнение 5 Чему равна эйлерова характеристика многогранника (В – Р + Г), где В – число
- 9. Упражнение 6 Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он
- 10. Упражнение 7 Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней,
- 11. Упражнение 8 Гранями выпуклого многогранника являются только четырехугольники. Сколько у него вершин и граней, если число
- 12. Упражнение 9 В каждой вершине выпуклого многогранника сходится по четыре ребра. Сколько он имеет вершин и
- 13. Упражнение 10 Как изменится число вершин, рёбер и граней выпуклого многогранника, если к одной из его
- 14. Упражнение 11 Как изменится число вершин, рёбер и граней выпуклого многогранника, если от него отсечь один
- 15. Упражнение 12* Докажите, что в любом выпуклом многограннике число треугольных граней плюс число трехгранных углов больше
- 16. Упражнение 13* Докажите, что в любом выпуклом многограннике имеется грань с числом сторон, меньшим шести. Доказательство.
- 18. Скачать презентацию











 Распознавание объектов на местности с помощью нейронных сетей
Распознавание объектов на местности с помощью нейронных сетей Методика подбора и анализа моделей аналогов
Методика подбора и анализа моделей аналогов Контрольна робота з теми Життя людей за первісних часів
Контрольна робота з теми Життя людей за первісних часів Основы ландшафтной колористики
Основы ландшафтной колористики Коррозия металлов и способы защиты
Коррозия металлов и способы защиты Лекция-презентация. Формирования позиции ответственного родительства.
Лекция-презентация. Формирования позиции ответственного родительства. Алкоголизм- это страшная беда современного общества
Алкоголизм- это страшная беда современного общества Жизнь и быт поволжских татар
Жизнь и быт поволжских татар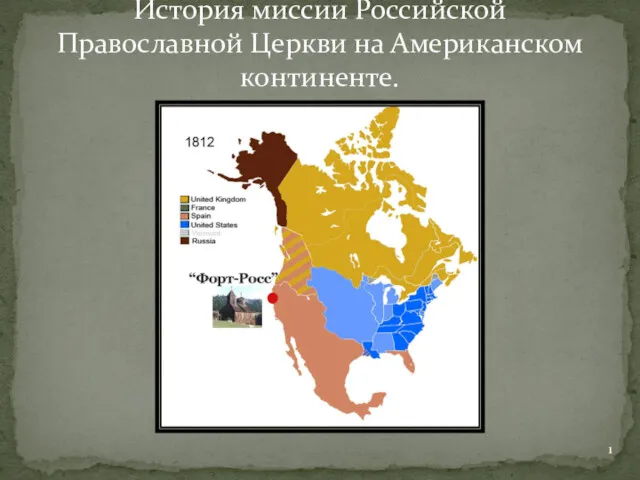 История миссии Российской Православной Церкви на Американском континенте
История миссии Российской Православной Церкви на Американском континенте практические работы
практические работы Создание на территории субъекта РФ площадок для обучения и творчества в сфере информационных технологий для детей ИТ-cube
Создание на территории субъекта РФ площадок для обучения и творчества в сфере информационных технологий для детей ИТ-cube Умножение дробей
Умножение дробей Вводная презентация к проекту Я - петербуржец.
Вводная презентация к проекту Я - петербуржец. Ремонт автомобильных дорог Чайковского муниципального района. 2018 год
Ремонт автомобильных дорог Чайковского муниципального района. 2018 год Доклад для воспитателей ДОУ на тему :Роль сказок в развитии детей дошкольного возраста
Доклад для воспитателей ДОУ на тему :Роль сказок в развитии детей дошкольного возраста Қаттылықты анықтау тәсілдер
Қаттылықты анықтау тәсілдер Великая Отечественная война.
Великая Отечественная война. Правила безопасного сексуального поведения
Правила безопасного сексуального поведения Презентация Листопадничек
Презентация Листопадничек Астраханский Кремль
Астраханский Кремль Food and fertilizers. Outline
Food and fertilizers. Outline Домашняя экономика
Домашняя экономика Константин Григорьевич Паустовский (1892-1968)
Константин Григорьевич Паустовский (1892-1968) Пассажирские сервисы
Пассажирские сервисы Вращающаяся печь для обжига портландцемента
Вращающаяся печь для обжига портландцемента PEShIE_EKSKURSII_2022
PEShIE_EKSKURSII_2022 Устройства ввода и вывода звука
Устройства ввода и вывода звука Интеллектуальная игра. Где логика
Интеллектуальная игра. Где логика