Содержание
- 2. ПОВТОРИМ…
- 3. ПОНЯТИЕ ПЕРВООБРАЗНОЙ Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем
- 4. ПРИМЕРЫ f(x) = 2x; F(x) = x2 F′(x)= (x2)′ = 2x = f(x) f(x) = –
- 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x) называют любую ее первообразную
- 6. ПРИМЕРЫ
- 7. ТАБЛИЦА ПЕРВООБРАЗНЫХ f(x) F(x) F(x)
- 8. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ 1º Если F(x) есть первообразная для f(x), а G(x) – первообразная для
- 9. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 10. Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен
- 11. Вычисление определенного интеграла
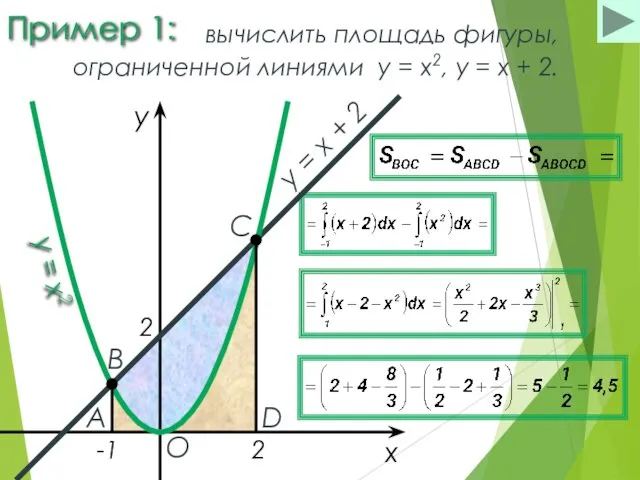
- 12. Пример 1: вычислить площадь фигуры, ограниченной линиями y = x2, y = x + 2. x
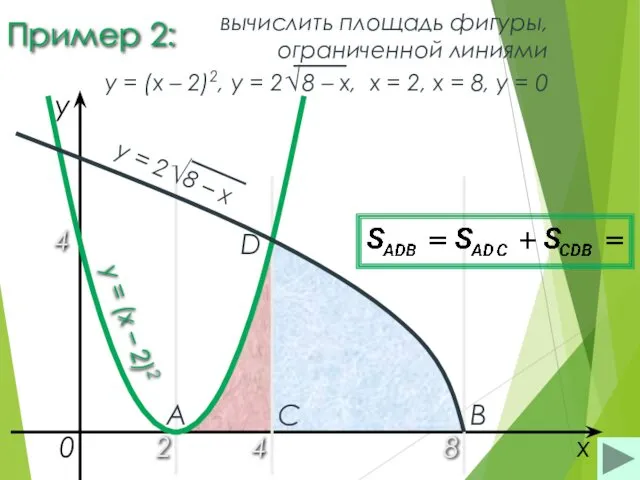
- 13. Пример 2: 2 8 x y = (x – 2)2 0 A B C D 4
- 14. Пример 2:
- 16. Скачать презентацию











 kak_stat_uspeshnym_chelovekom
kak_stat_uspeshnym_chelovekom Логика. Умозаключение
Логика. Умозаключение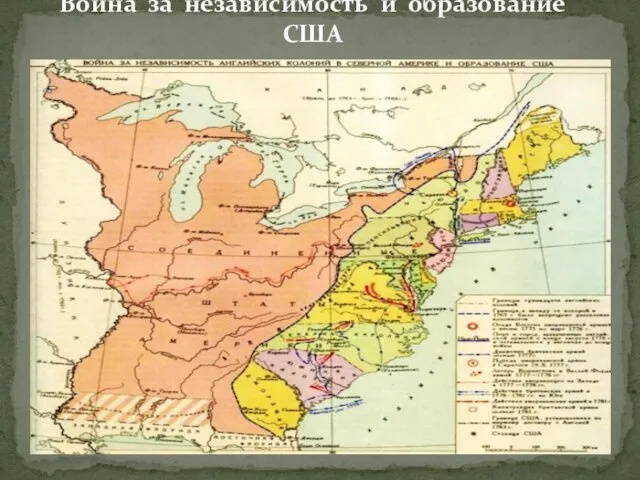 Война за независимость и образование США
Война за независимость и образование США Виды сов
Виды сов Презентация по географии в 10 классе по теме Научно-техническая революция и Мировое хозяйство
Презентация по географии в 10 классе по теме Научно-техническая революция и Мировое хозяйство Нормативная база по противодействию курению
Нормативная база по противодействию курению Способы обнаружения и устранения неисправностей и последовательность проверки работоспособности радиоприемника
Способы обнаружения и устранения неисправностей и последовательность проверки работоспособности радиоприемника 1_Введение
1_Введение Профессии будущего
Профессии будущего Социальная структура общества
Социальная структура общества Present continuous
Present continuous Поверхности нагрева паровых котлов
Поверхности нагрева паровых котлов Фотосинтез процесі
Фотосинтез процесі Фразеология. Фразеологические сращения. Фразеологические единства
Фразеология. Фразеологические сращения. Фразеологические единства ОМРК Добро и зло.
ОМРК Добро и зло. Всемирная сеть СТО. Компания Bosch
Всемирная сеть СТО. Компания Bosch Сүйек буын туберкулезі
Сүйек буын туберкулезі Методы арт-терапии в образовательном процессе ДОУ
Методы арт-терапии в образовательном процессе ДОУ Лабораторная диагностика вирусных инфекций
Лабораторная диагностика вирусных инфекций Ветер
Ветер Электроэнергетика мира
Электроэнергетика мира Дидактические игры по ФЭМП по Тихеевой
Дидактические игры по ФЭМП по Тихеевой Компоновка поперечной рамы
Компоновка поперечной рамы Презентация Несуществующие дорожные знаки Диск
Презентация Несуществующие дорожные знаки Диск Тематика задач на ЕГЭ по математике
Тематика задач на ЕГЭ по математике Интеллектуальная игра Брей-ринг
Интеллектуальная игра Брей-ринг Артикуляционная гимнастика
Артикуляционная гимнастика Новые подходы к изучению истории Великой Отечественной войны и их отражение в школьных учебниках
Новые подходы к изучению истории Великой Отечественной войны и их отражение в школьных учебниках