Метод наименьших квадратов
2. Класс аппроксимирующих функций
В качестве аппроксимирующей функции будем
принимать многочлен некоторой степени m.
Здесь – параметры модели, являющиеся коэффициентами
многочлена .
3. Выбор критерия согласия
Как нетрудно видеть, при интерполировании происходит повторение ошибок
наблюдений, в то время как при обработке экспериментальных данных
желательно, напротив, их сглаживание.
Отказываясь от требования выполнения в точках точных равенств, следует все
же стремиться к тому, чтобы в этих точках выполнялись соответствующие
приближенные равенства . Из различных критериев, позволяющих
выбрать параметры модели так, чтобы приближенные равенства
удовлетворялись наилучшим в некотором смысле образом,
наиболее часто используется критерий наименьших квадратов. Согласно этому
критерию параметры выбираются так, чтобы минимизировать
среднеквадратичное уклонение многочлена от заданных
табличных значений .













 дыхательная недостаточность
дыхательная недостаточность Родительское собрание в 1 классе
Родительское собрание в 1 классе Царь Соломон
Царь Соломон Презентация_Селяева А.Д
Презентация_Селяева А.Д Квалификационная работа Совершенствование ротации сотрудников на розничном торговом предприятии ООО Пламя
Квалификационная работа Совершенствование ротации сотрудников на розничном торговом предприятии ООО Пламя Оңтүстік Американың халқы және елдері. Анд тауындағы биіктік белдеулер
Оңтүстік Американың халқы және елдері. Анд тауындағы биіктік белдеулер Организация, содержание, приницпы подготовки школьников к олимпиадам по географии от школьных до международных
Организация, содержание, приницпы подготовки школьников к олимпиадам по географии от школьных до международных Консультация для воспитателей Здоровьесбережение педагога
Консультация для воспитателей Здоровьесбережение педагога Синустық брадикардия
Синустық брадикардия Модели аргументирующей коммуникации
Модели аргументирующей коммуникации Художні промисли України
Художні промисли України Управление персоналом предприятия в кризисных ситуациях. Тема № 12
Управление персоналом предприятия в кризисных ситуациях. Тема № 12 Презентация к проекту Учимся безопасности по сказкам
Презентация к проекту Учимся безопасности по сказкам Печатная реклама. Приюты для животных
Печатная реклама. Приюты для животных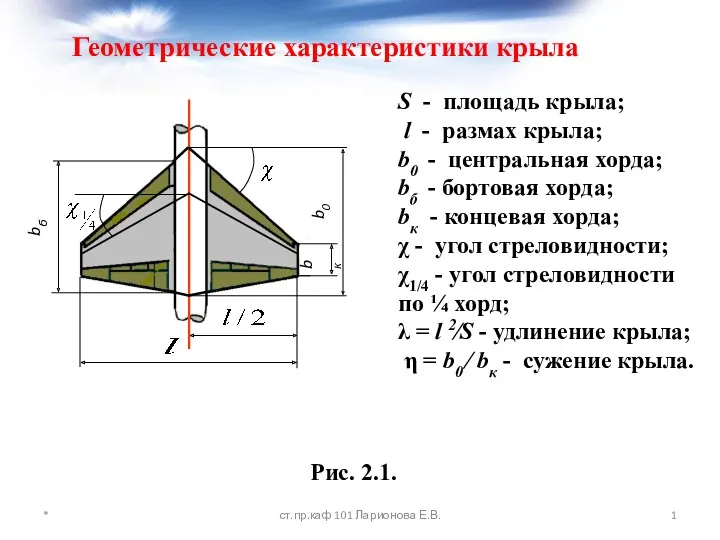 Геометрические характеристики крыла
Геометрические характеристики крыла Презентация к уроку химии 8 класс по теме Растворение. Растворимость веществ в воде
Презентация к уроку химии 8 класс по теме Растворение. Растворимость веществ в воде Краткая история средств связи и информации
Краткая история средств связи и информации Сравнение чисел. 6 класс
Сравнение чисел. 6 класс Подготовка к написанию сочинения. Определение проблемы исходного текста
Подготовка к написанию сочинения. Определение проблемы исходного текста Атмосферное давление
Атмосферное давление Курсовой проект. Жилой дом на две семьи
Курсовой проект. Жилой дом на две семьи Великие путешественники. Интерактивный тест
Великие путешественники. Интерактивный тест Системы счисления. Кодирование чисел целых и дробных. Лекция 2
Системы счисления. Кодирование чисел целых и дробных. Лекция 2 фрагмент урока для 3 класса на тему Дружба
фрагмент урока для 3 класса на тему Дружба Отвод поверхностных вод. Водосборно-водоотводные сооружения (водоотводы)
Отвод поверхностных вод. Водосборно-водоотводные сооружения (водоотводы) ФОРМИРОВАНИЕ ПРЕДИКАТИВНОГО СЛОВАРЯ В РАСПРОСТРАНЕННОМ ПРЕДЛОЖЕНИИ У ДОШКОЛЬНИКОВ С НАРУШЕНИЕМ РЕЧИ 5-6 ЛЕТ.
ФОРМИРОВАНИЕ ПРЕДИКАТИВНОГО СЛОВАРЯ В РАСПРОСТРАНЕННОМ ПРЕДЛОЖЕНИИ У ДОШКОЛЬНИКОВ С НАРУШЕНИЕМ РЕЧИ 5-6 ЛЕТ. Участник конкурса Лучшее территориальное общественное самоуправление ТОС Мегрегские карелы
Участник конкурса Лучшее территориальное общественное самоуправление ТОС Мегрегские карелы Аварийно химически опасные вещества
Аварийно химически опасные вещества