Содержание
- 2. Қайсыбір көлемдегі зарядтың уақыт бойынша өзгерісі: туындысымен беріледі
- 3. Екінші жағынан, бірлік уақыттағы өзгеріс осы уақыттың ішінде берілген көлемнен шығатын немесе керісінше, оның ішіне кіретін
- 4. . Сондықтан егер заряд біздің көлемнен шығатын болса, ρvdf оң да, ал заряд оған кіретін болса
- 5. Алынған екі өрнекті салыстыра отырып, (29,1) деп табамыз. Оң жақта минус таңбасы қойылған , себебі егер
- 6. Зарядтың сақталу заңын білдіретін теңдеу (29,1) дегеніміз интегралдық түрде жазылған үзіксіздік теңдеуі болып табылады. ρv дегеніміздің
- 7. Бұл теңдеуді дифференциалдық түрде жазамыз. (29,2)-нің оң жағында Гаусс теоремасын, яғни қолданып, деп табамыз. Бұл теңдік
- 8. . Бұл теңдік кез келген көлем бойынша интегралдаған кезде орындалуы тиіс блғандықтан , инеграл астындағы өрнек
- 9. δ-функция түрінде ρ үшін жазылған (28,1) өрнектің (29,3) теңдеуді автоматты түрде қанағаттандыратындығына оңай көз жеткізуге болады.
- 10. Сондықтан Бірақ дегеніміз зарядтың v жылдамдығы ғой. Одан әрі ρ дегеніміз айырмасының функциясы болатындықтан, Демек ,
- 11. Төртөлшемдік түрде (29,3) үздіксіздіктің теңдеуі тоқтың 4-векторының 4-дивергенциясының нөлге теңдігімен өрнектеледі: (29,4) Өткен параграфта біз тұтас
- 12. Басқа уақыт мезетінде толық заряд басқа, осіне перпендикуляр болатын гипербет бойынша алынған осындай интегралмен өрнектелді. (29,4)
- 13. (29,5) болғандығына көз жеткізуге болады. Міне, дәлелдемек болғанымыз осы еді. Келтірілген дәлелдеменің интегралдау (үшөлшемдік) кеңістікті түгел
- 14. Біз электродинамика теңдеулерінің калибрлік инварианттылығы мен зарядтың сақталу заңының арасындағы тығыз байланыс жайлы сөз еткенбіз. Оны
- 16. Скачать презентацию













 Природоведение - урок по тема: Астероиды и кометы.
Природоведение - урок по тема: Астероиды и кометы. Деривационные водоводы ГЭС. Лекция 17
Деривационные водоводы ГЭС. Лекция 17 Перси Биш Шелли (1792 –1822)
Перси Биш Шелли (1792 –1822)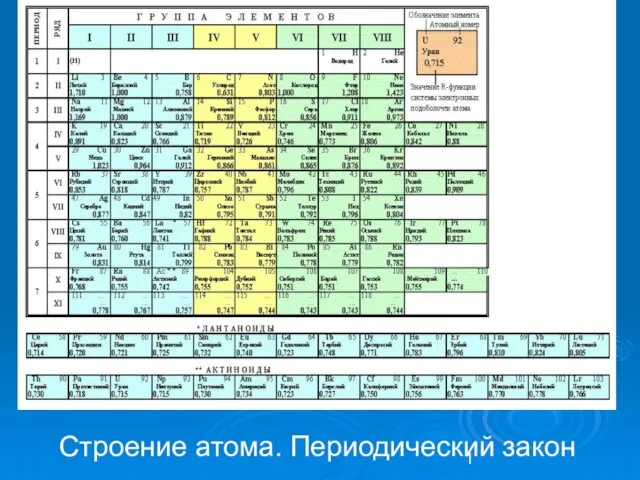 Строение атома. Периодический закон
Строение атома. Периодический закон Психолого- педагогические аспекты работы с родителями при формировании самооценки
Психолого- педагогические аспекты работы с родителями при формировании самооценки Особенности собственных нужд АЭС с реакторами БН. (Лекция 5)
Особенности собственных нужд АЭС с реакторами БН. (Лекция 5) Лицевой нерв
Лицевой нерв Презентация по химии для 10 класса Гормоны. Лекарства
Презентация по химии для 10 класса Гормоны. Лекарства Патриархальная теория происхождения государства
Патриархальная теория происхождения государства macbook
macbook Информационный ресурс МГС
Информационный ресурс МГС Моя воспитательная система
Моя воспитательная система Семь шагов к успеху, или основные правила разработки проекта
Семь шагов к успеху, или основные правила разработки проекта Хореографическое искусство в России: истоки и эволюция
Хореографическое искусство в России: истоки и эволюция Интерфейсы микропроцессорных систем. Способы использования микропроцессорных систем в радиоэлектронных устройствах
Интерфейсы микропроцессорных систем. Способы использования микропроцессорных систем в радиоэлектронных устройствах Советы первоклассникам
Советы первоклассникам Презентация дополнительной образовательной программы Планета фитнес
Презентация дополнительной образовательной программы Планета фитнес По городам Австралии
По городам Австралии Памятники природы национального парка ТАГАНАЙ
Памятники природы национального парка ТАГАНАЙ презентация Как размножаются живые организмы
презентация Как размножаются живые организмы Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций. (рсчс)
Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций. (рсчс) Задержание в качестве подозреваемого
Задержание в качестве подозреваемого Урок математики в 6 классе Сравнение положительных и отрицательных чисел
Урок математики в 6 классе Сравнение положительных и отрицательных чисел Магия в первобытной культуре. Виды, приемы, механизмы
Магия в первобытной культуре. Виды, приемы, механизмы презентация Новый закон об образовании для родителей
презентация Новый закон об образовании для родителей Функции управления
Функции управления Праздник непослушания
Праздник непослушания Конструкции паровых котельных агрегатов
Конструкции паровых котельных агрегатов