Содержание
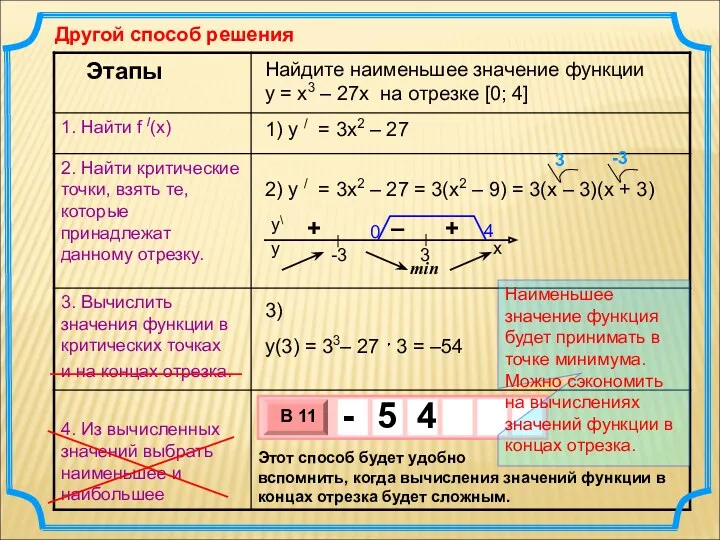
- 2. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 3. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
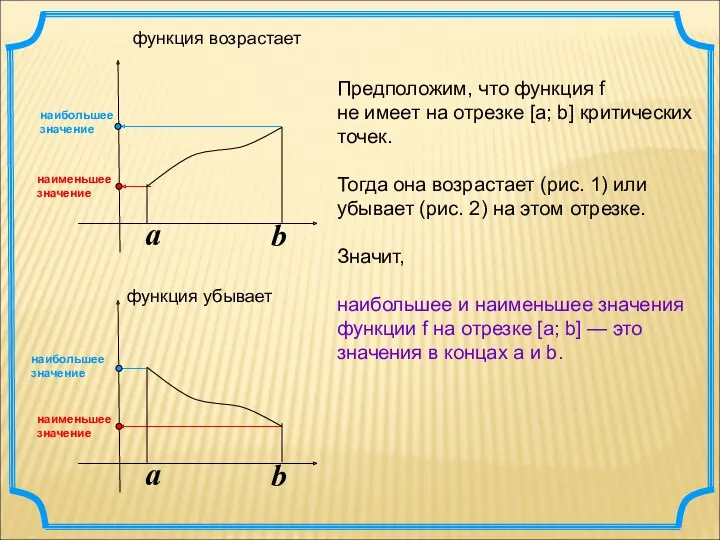
- 4. a b a b Предположим, что функция f не имеет на отрезке [а; b] критических точек.
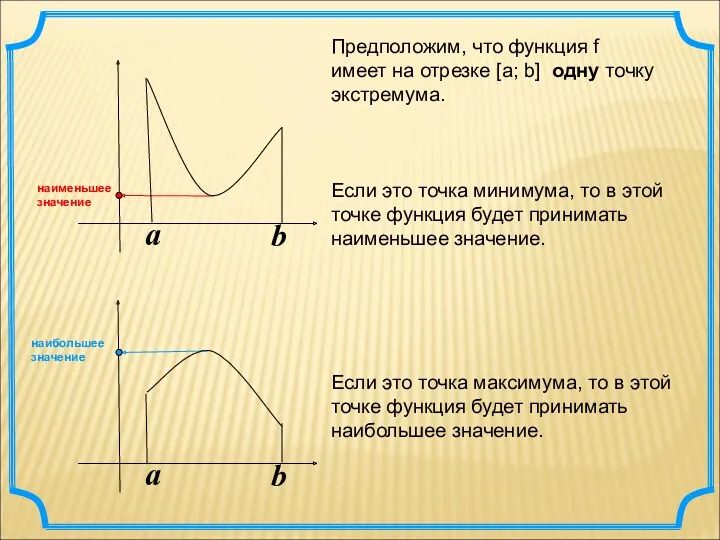
- 5. a b a b Предположим, что функция f имеет на отрезке [а; b] одну точку экстремума.
- 6. Сложная функция
- 7. СЛОЖНАЯ ФУНКЦИЯ – функция, представленная как композиция нескольких функций. Сложная функция – функция от функции. Сложная
- 8. Чтобы найти производную сложной функции, нужно: Определить, какая функция является внешней и найти по таблице производных
- 9. Функция промежуточного аргумента – квадратичная функция Функция квадратного корня Показательная функция Функция промежуточного аргумента – квадратичная
- 10. Проверим, принадлежит ли х=ln3 промежутку [1; 2] Найдите наименьшее значение функции y = e2x – 6ex
- 11. Найдите наибольшее значение функции 2. x = – 2 Найдем критические точки, которые принадлежат D(у). Вычислим
- 12. При решении некоторых заданий на вычисление наибольшего и наименьшего значений функции можно найти ответ и без
- 13. Найдите наибольшее значение функции 2. 2 способ Решим задание без вычисления производной. Функция квадратного корня монотонно
- 14. Найдите наименьшее значение функции 4. x = - 1 Найдем критические точки, которые принадлежат D(у). Вычислим
- 15. Найдите наименьшее значение функции 4. Решим задание без вычисления производной. Показательная функция с основанием 2>1 монотонно
- 16. Найдите наибольшее значение функции 6. Решим задание без вычисления производной. Логарифмическая функция с основанием 5 является
- 17. ЧТО ОБЩЕГО МЕЖДУ ФУНКЦИЕЙ, ЗАБОРОМ И КЛУБНИКОЙ?
- 18. « Самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что, прежде чем строить
- 19. Задача : Какими должны быть размеры участка прямоугольной формы площадью , чтобы на его ограждение было
- 20. ИЗ ВСЕХ ПРЯМОУГОЛЬНИКОВ ПЛОЩАДЬЮ 1600 КВ. М НАЙТИ ПРЯМОУГОЛЬНИК НАИМЕНЬШЕГО ПЕРИМЕТРА. 1. Р – периметр прямоугольника
- 21. x = 40 – точка минимума, значит функция р ( х ) в этой точке принимает
- 22. Длина участка – 40 ( м ) Ширина участка – 40 м Длина прямоугольника – 40
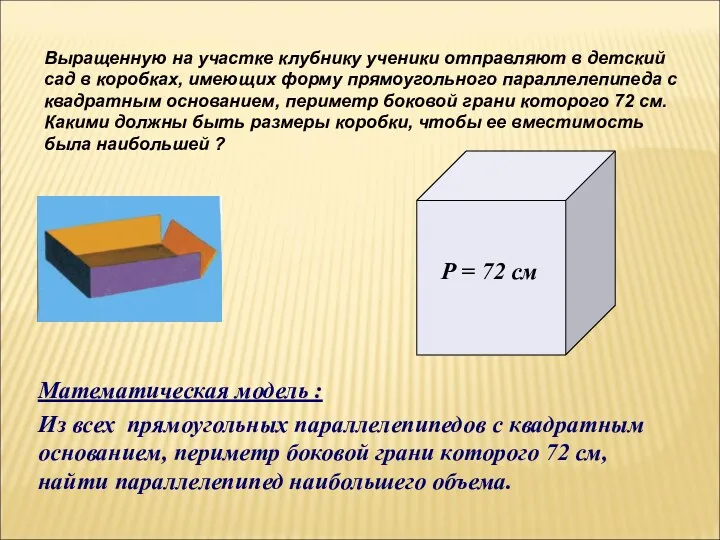
- 23. Задача : Выращенную на участке клубнику ученики отправляют в детский сад в коробках, имеющих форму прямоугольного
- 24. Математическая модель : Из всех прямоугольных параллелепипедов с квадратным основанием, периметр боковой грани которого 72 см,
- 25. Из всех прямоугольных параллелепипедов с квадратным основанием, периметр боковой грани которого 72 см, найти параллелепипед наибольшего
- 26. x = 24 – точка максимума, значит функция v ( х ) в этой точке принимает
- 27. Длина прямоугольного параллелепипеда – 24 ( см ) Ширина прямоугольного параллелепипеда – 24 ( см )
- 29. Скачать презентацию





![Проверим, принадлежит ли х=ln3 промежутку [1; 2] Найдите наименьшее значение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/472923/slide-9.jpg)
















 Урок - проект по теме Действия с десятичными дробямис применением здоровьесберегающих технологий
Урок - проект по теме Действия с десятичными дробямис применением здоровьесберегающих технологий Решение уравнений с помощью систем
Решение уравнений с помощью систем Урок математики по теме Пропорция
Урок математики по теме Пропорция Разработка урока по математике в 9 классе , по теме Геометрическая прогрессия
Разработка урока по математике в 9 классе , по теме Геометрическая прогрессия Презентация к уроку Умножение и деление обыкновенных дробей
Презентация к уроку Умножение и деление обыкновенных дробей Слайд-презентация по теме Возрастание и убывание функций
Слайд-презентация по теме Возрастание и убывание функций внеклассное мероприятие 5класс кто хочет стать отличником
внеклассное мероприятие 5класс кто хочет стать отличником Рекомендации по разработке программы развития универсальных учебных действий
Рекомендации по разработке программы развития универсальных учебных действий Урок - игра Восхождение на пик Победы
Урок - игра Восхождение на пик Победы Урок алгебры в 11 классе по теме: Производная некоторых элементарных функций
Урок алгебры в 11 классе по теме: Производная некоторых элементарных функций Арифметическая прогрессия
Арифметическая прогрессия Ох,уж эта математика!
Ох,уж эта математика! Презентация к уроку в 6 классе
Презентация к уроку в 6 классе презентация Пропаганда здорового образа жизни на уроках математики
презентация Пропаганда здорового образа жизни на уроках математики Глава 9_параграф 54. Случайные события и их вероятности. Часть 1. ИСПОЛЬЗОВАНИЕ КОМБИНАТОРИКИ ДЛЯ ПОДСЧЕТА ВЕРОЯТНОСТЕЙ.
Глава 9_параграф 54. Случайные события и их вероятности. Часть 1. ИСПОЛЬЗОВАНИЕ КОМБИНАТОРИКИ ДЛЯ ПОДСЧЕТА ВЕРОЯТНОСТЕЙ. Презентация Все есть число
Презентация Все есть число Презентация к внеклассному мероприятию в 6 классе Свистать всех наверх!
Презентация к внеклассному мероприятию в 6 классе Свистать всех наверх! Конспект и презентация к уроку математики 6 класс Преобразование обыкновенных дробей в десятичные
Конспект и презентация к уроку математики 6 класс Преобразование обыкновенных дробей в десятичные Дробь от числа и число по его дроби
Дробь от числа и число по его дроби Проект Квадратные уравнения
Проект Квадратные уравнения Графики элементарных функций часть 1
Графики элементарных функций часть 1 Час занимательной математики
Час занимательной математики Урок алгебры по теме Формулы квадрата суммы и квадрата разности двух выражений
Урок алгебры по теме Формулы квадрата суммы и квадрата разности двух выражений решение задач на нахождение части от целого и целого по его части
решение задач на нахождение части от целого и целого по его части Презентация Занимательная математика
Презентация Занимательная математика Внеклассное мероприятие по математике для 9 класса Знатоки математики
Внеклассное мероприятие по математике для 9 класса Знатоки математики Квадратные уравнения
Квадратные уравнения Урок математики по теме Действия с десятичными дробями
Урок математики по теме Действия с десятичными дробями