Открытый урок с использованием информационных технологии по теме Решение уравнений, содержащих знак абсолютной величины. презентация
Содержание
- 2. ТЕМА: Решение уравнений
- 3. ТЕМА: Решение уравнений, содержащих знак абсолютной величины (модуль).
- 4. ЦЕЛЬ: Повторить и закрепить знания по теме «Модуль числа». Научиться решать уравнения вида: |f(х)| = a
- 5. 1. Разминка. Дайте определение модуля числа.
- 6. Устная работа. Раскрыть модуль:
- 7. | π -3| | √5+√3| π -3 √5+√3 √2-1 x4+1 √5 - 2 x2 |a -
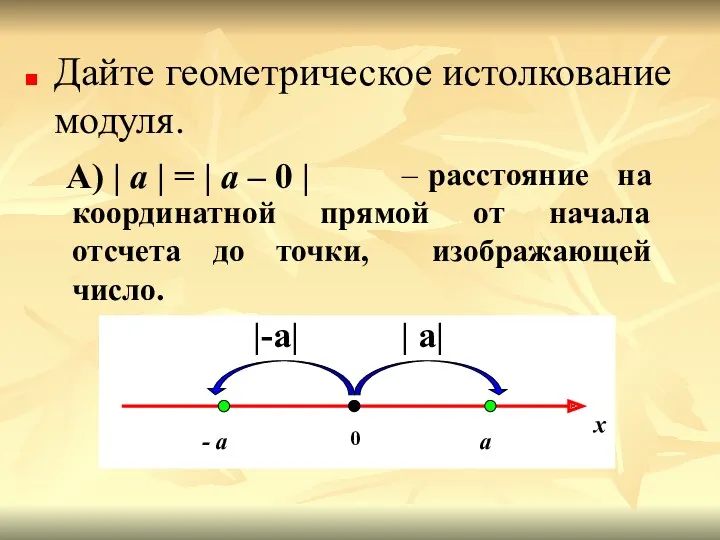
- 8. Дайте геометрическое истолкование модуля. А) | а | = | а – 0 | 0 а
- 9. Что такое | a – b | с точки зрения расстояния? Б) |a - b| -
- 10. Игра «Домино» Решите уравнения: |f(х)| = a
- 11. Уравнения вида |f(х)| = a Если а>0, то …… 2 корня. то …... 1 корень. корней
- 12. Пример 1. |x – 8|=5 Решение: По определению модуля имеем совокупность уравнений: откуда Ответ: 13;3.
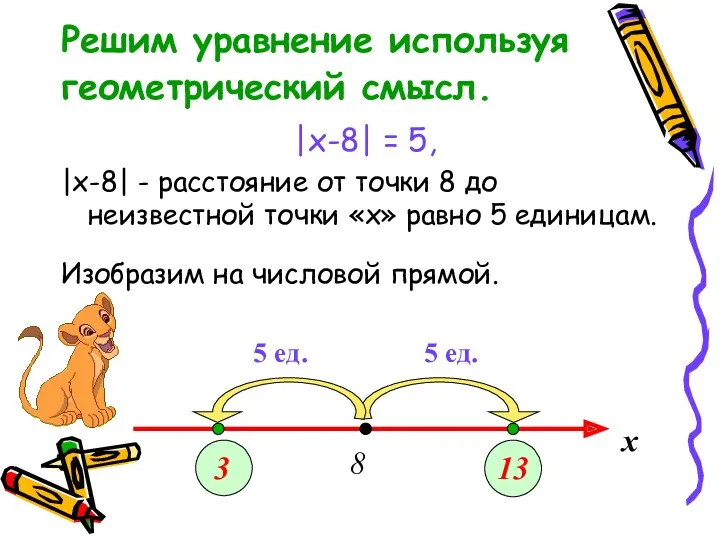
- 13. Решим уравнение используя геометрический смысл. |x-8| = 5, |x-8| - расстояние от точки 8 до неизвестной
- 14. Решить уравнения: а) |7 - x| = 8, б) |9 + x| +1 = 1, в)
- 15. Дополнительно: 2|X|+ 3 = 24 - 5|X| Решение: 2|X|+ 3 = 24 - 5|X| 2|X|+ 5|X|=24-3
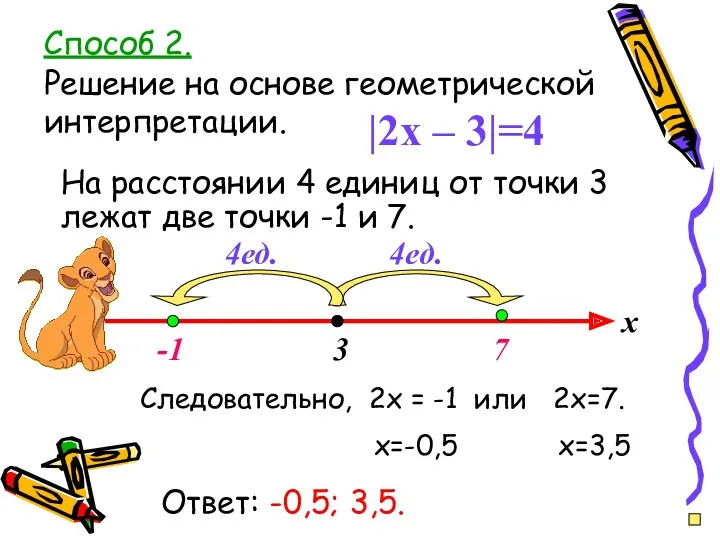
- 16. Пример 2. |2x – 3|=4 Решить самостоятельно. Способ 1. По определению модуля имеем: откуда Ответ: 3,5;
- 17. Способ 2. Решение на основе геометрической интерпретации. На расстоянии 4 единиц от точки 3 лежат две
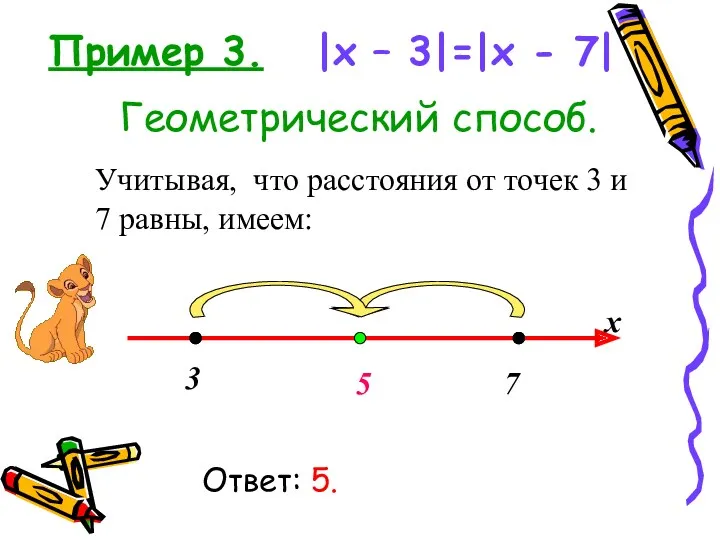
- 23. Геометрический способ. Учитывая, что расстояния от точек 3 и 7 равны, имеем: 3 7 х 5
- 24. Способ 2: |x – 3|=|x - 7| Решение: Данное уравнение равносильно двум уравнениям: х-3 = х–7
- 25. Уравнения вида |f(х)| = |g(x)| Данное уравнение равносильно совокупности
- 26. Решить уравнения: а) |х-2|=|5-х|, б) |4х-1|=|2х+3|. Дополнительно: |х + 2| = 2|3 - х|
- 27. Дополнительно: |х + 2| = 2|3 - х| Решение: откуда Ответ: 4/3; 8
- 28. Уравнения с модулем |f(х)| = |g(x)| Данное уравнение равносильно совокупности |f(х)| = a При а 0
- 29. Самостоятельная работа. 1) | 2Х+5 | = 7 2) | Х + 3 | = |х
- 30. Оцените себя: 1 уравнение – 1 балл, 2 уравнения - 2 балла, 3 уравнения – 3
- 31. 3) Уравнения вида 1) f (|x|) = а 2) |f(x)|= |g(х)| 3) |f(x)| + |g(x)| =
- 32. Задание на дом: Решить уравнения: а) | Х+2 | -6 = 16, б) ||2x-5| -3| =
- 34. Скачать презентацию











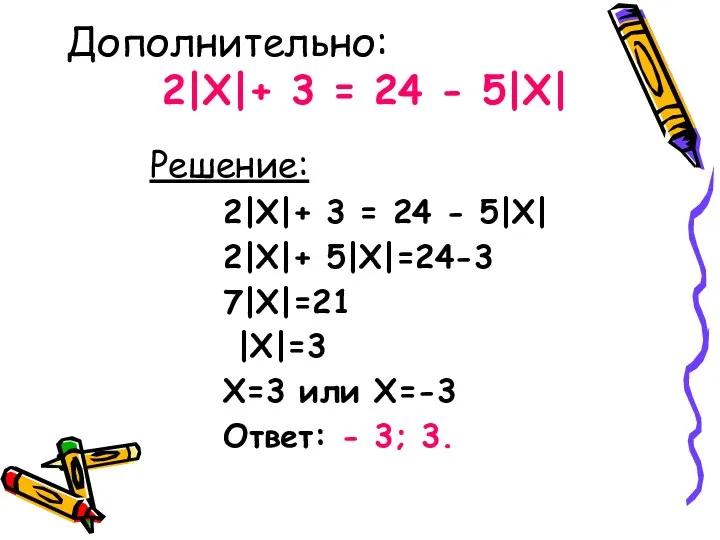













 Меры длины
Меры длины Подготовка к ЕГЭ по теме Практический расчёт, оценка и прикидка
Подготовка к ЕГЭ по теме Практический расчёт, оценка и прикидка презентация Площадь прямоугольника
презентация Площадь прямоугольника Сложение отрицательных чисел
Сложение отрицательных чисел Система подготовки к ГИА с использованием современных образовательных технологий
Система подготовки к ГИА с использованием современных образовательных технологий Презентация к уроку Введение в теорию вероятностей
Презентация к уроку Введение в теорию вероятностей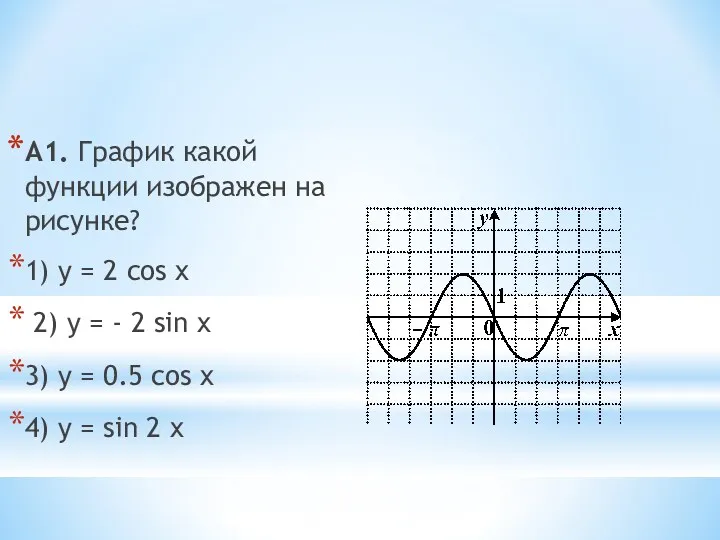 Конспект урока алгебры в 10 классе по теме Тригонометрические уравнения
Конспект урока алгебры в 10 классе по теме Тригонометрические уравнения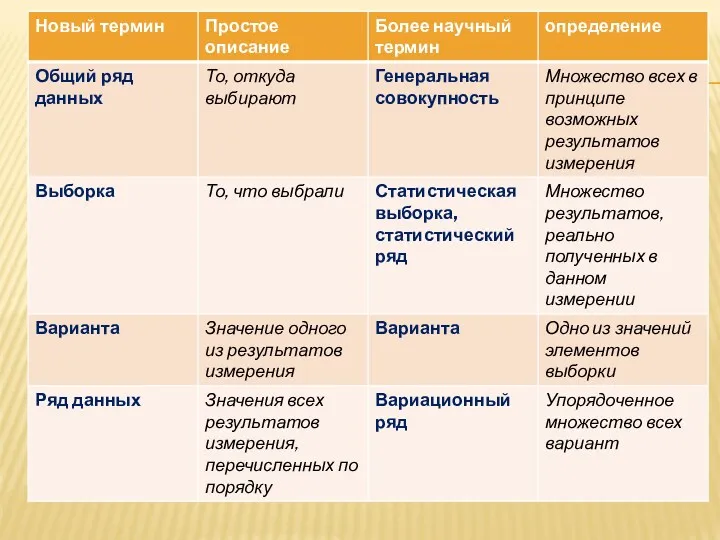 теория вероятности выборка....
теория вероятности выборка.... презентация к уроку математики Действия с рациональными числами
презентация к уроку математики Действия с рациональными числами методические рекомендации по теме: Тексты задач. Проценты. Цена, количество, стоимость.
методические рекомендации по теме: Тексты задач. Проценты. Цена, количество, стоимость. Презентация к уроку по алгебре 7 класс
Презентация к уроку по алгебре 7 класс презентация Из истории решения уравнений
презентация Из истории решения уравнений Рациональные числа. 6 класс.
Рациональные числа. 6 класс. Приложение 4 к уроку 3) Повторение и подготовка к экзамену в 9 классе
Приложение 4 к уроку 3) Повторение и подготовка к экзамену в 9 классе Факультатив Алгебра. Геометрия. Комбинаторика.
Факультатив Алгебра. Геометрия. Комбинаторика. Математический кубик-рубик
Математический кубик-рубик Современные методы повышения мотивации на уроках математики
Современные методы повышения мотивации на уроках математики Возрастание и убывание функции. Экстремумы функции. 11 класс
Возрастание и убывание функции. Экстремумы функции. 11 класс Нужен ли учебник ученику для изучения темы Параметры в 8-9 классе?
Нужен ли учебник ученику для изучения темы Параметры в 8-9 классе? Разработка обобщающего урока по математике в 5 классе по теме: Действия с натуральными числами
Разработка обобщающего урока по математике в 5 классе по теме: Действия с натуральными числами Первые инструменты для счёта
Первые инструменты для счёта Построение кусочно-заданных функций с помощью программы Advanced Grapher
Построение кусочно-заданных функций с помощью программы Advanced Grapher Применение теоремы Виета (2 урок)
Применение теоремы Виета (2 урок) Тест-тренажер Умножение десятичных дробей
Тест-тренажер Умножение десятичных дробей Сложение отрицательных чисел и чисел с разными знаками 6 класс
Сложение отрицательных чисел и чисел с разными знаками 6 класс Презентация Своя игра к уроку математики по теме Обыкновенные дроби.
Презентация Своя игра к уроку математики по теме Обыкновенные дроби. Обобщающий урок по математике в 5 классе по темеФормулы
Обобщающий урок по математике в 5 классе по темеФормулы Презентация к уроку по теме Функция и ее график
Презентация к уроку по теме Функция и ее график