Содержание
- 2. Применение производной К исследованию функции
- 5. 3 2 1
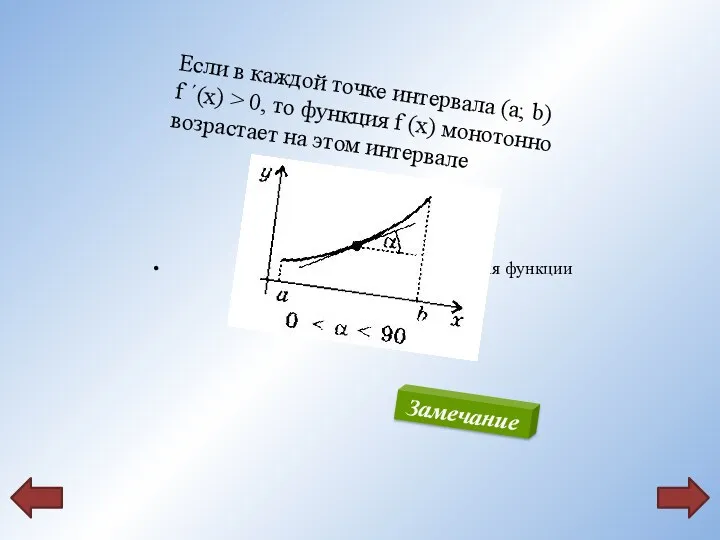
- 6. Если в каждой точке интервала (a; b) f ´(x) > 0, то функция f (x) монотонно
- 7. Замечание Приведенные условия являются только достаточными Условиями монотонности, но не являются необходимыми. Например, функция y =
- 8. Если в каждой точке интервала (a; b) f ´(x) убывает на этом интервале Замечание
- 9. Функция f (x) постоянна на интервале (a; b) тогда и только тогда, когда f ´(x) =
- 10. Если x ̻ - точка экстремума функции y = f(x), то эта точка является критической точкой
- 11. Замечание Приведенное условие является только необходимым условием экстремума, но не являются достаточным: критическая точка не обязательно
- 12. Если y = f(x) непрерывна в точке x ̻ и производная f ´(x) меняет знак в
- 13. Замечание В самой точке x ̻ производной y функции y = f(x) может не существовать .
- 14. Схема применения производной для нахождения интервалов монотонности и экстремумов 1 Найдите область определения функции и интервалы,
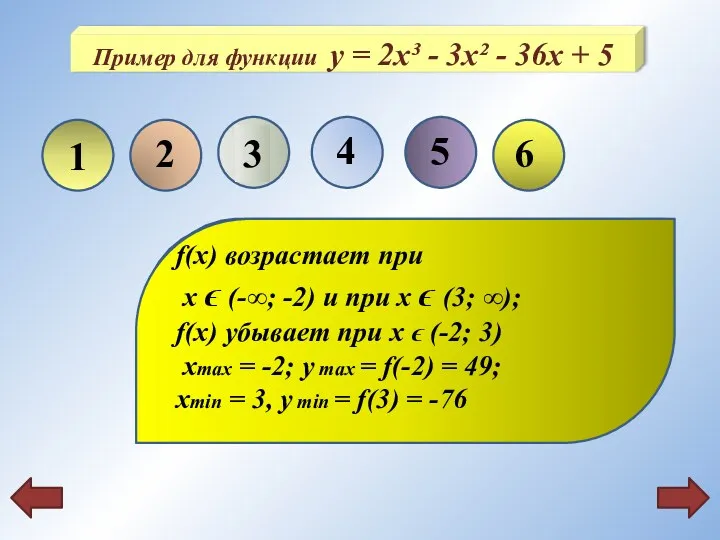
- 15. 1 Область определения: R. Функция непрерывна во всей области определени f ´(x) = 6x² - 6x
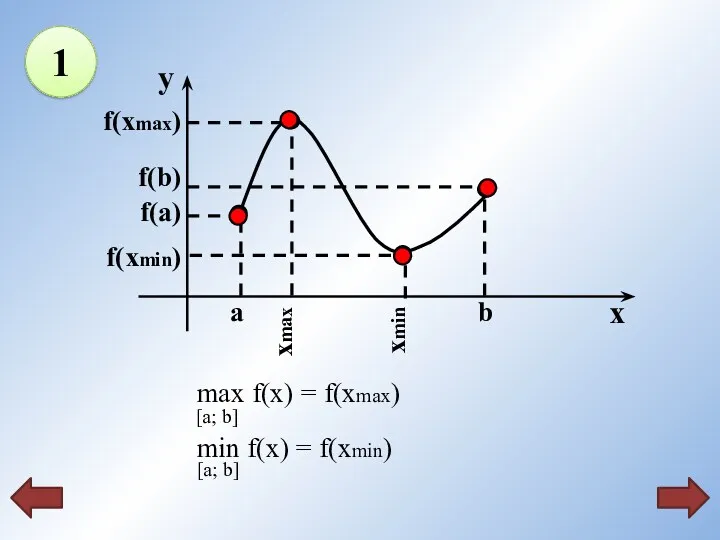
- 16. f(xmin) f(xmax) f(a) f(b) a b xmax xmin 1
- 17. f(xmax) f(a) f(b) a b xmax 2
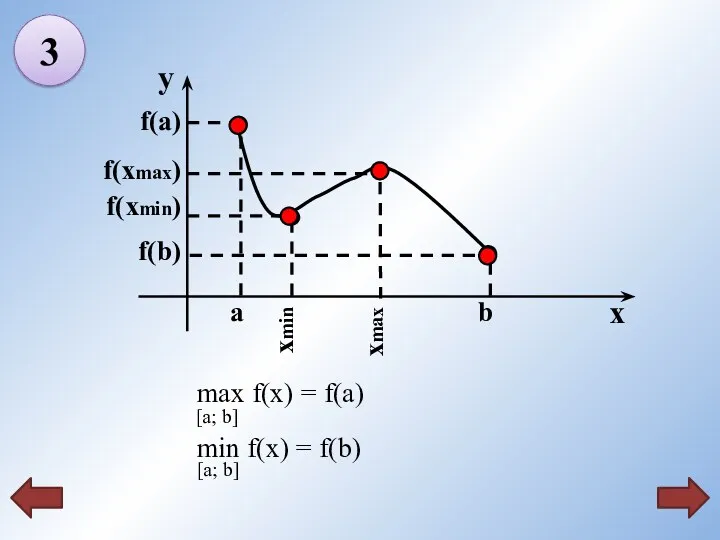
- 18. f(xmin) f(xmax) f(a) f(b) a b xmax xmin 3
- 19. Схема нахождения наибольшего и наименьшего значений функции , непрерывной на отрезке 1 Найдите производную f ´(x).
- 20. 1 f ´(x) = 6x² - 6x -36. f ´(x) = 0 при x = -2
- 22. Скачать презентацию














 Презентация по алгебре на тему Графический способ решения задач с параметрами
Презентация по алгебре на тему Графический способ решения задач с параметрами Урок путешествие по сказке Колобок. Математика 5 класс. Диск
Урок путешествие по сказке Колобок. Математика 5 класс. Диск Урок алгебры для 8 класса по теме Построение графиков функций, содержащих знак модуля
Урок алгебры для 8 класса по теме Построение графиков функций, содержащих знак модуля Абсолютная величина (элективный курс), 9 класс, презентация
Абсолютная величина (элективный курс), 9 класс, презентация Иррациональные уравнения
Иррациональные уравнения Функция арифметического квадратного корня
Функция арифметического квадратного корня презентация по теме История тригонометрии
презентация по теме История тригонометрии Урок в 10 классе по алгебре и началам анализа Свойства корней n-ой степени
Урок в 10 классе по алгебре и началам анализа Свойства корней n-ой степени Урок Построение графика функции с помощью производной Приложение 1
Урок Построение графика функции с помощью производной Приложение 1 Презентация к уроку Урок – смотр знаний в 5 класс по математике. Тема урока: Сложение и вычитание десятичных дробей.
Презентация к уроку Урок – смотр знаний в 5 класс по математике. Тема урока: Сложение и вычитание десятичных дробей. Длина окружности
Длина окружности Короткова Н.А. Обобщающий урок по теме: Натуральные числа 5кл Анализ урока
Короткова Н.А. Обобщающий урок по теме: Натуральные числа 5кл Анализ урока ФОРМИРОВАНИЕ КЛЮЧЕВЫХ КОМПЕТЕНЦИЙ НА УРОКЕ МАТЕМАТИКИ.
ФОРМИРОВАНИЕ КЛЮЧЕВЫХ КОМПЕТЕНЦИЙ НА УРОКЕ МАТЕМАТИКИ. Графический способ решения систем уравнений, 9 класс
Графический способ решения систем уравнений, 9 класс Презентация по теме Решение задач на сплавы и смеси
Презентация по теме Решение задач на сплавы и смеси Презентация к развивающему занятию Теория графов
Презентация к развивающему занятию Теория графов Презентация Тапкырлаучыны тамыр тамгасы астына кертү,тапкырлаучыны тамыр тамгасы астыннан чыгару , 8 класс
Презентация Тапкырлаучыны тамыр тамгасы астына кертү,тапкырлаучыны тамыр тамгасы астыннан чыгару , 8 класс Урок Путешествие на математическом поезде по стране Десятичная дробь
Урок Путешествие на математическом поезде по стране Десятичная дробь Презентация по математике для 6 класса на тему Сложение и вычитание рациональных чисел.
Презентация по математике для 6 класса на тему Сложение и вычитание рациональных чисел. Анализ пробных тестирований ( в формате ЕГЭ) по математике
Анализ пробных тестирований ( в формате ЕГЭ) по математике Презентация к внеклассному мероприятию в 6 классе Свистать всех наверх!
Презентация к внеклассному мероприятию в 6 классе Свистать всех наверх! Особенности решения различных типов задач - задачи краеведческого, исторического содержания.
Особенности решения различных типов задач - задачи краеведческого, исторического содержания. Целые числа 6 класс (устная работа)
Целые числа 6 класс (устная работа) Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Арифметическая прогрессия
Арифметическая прогрессия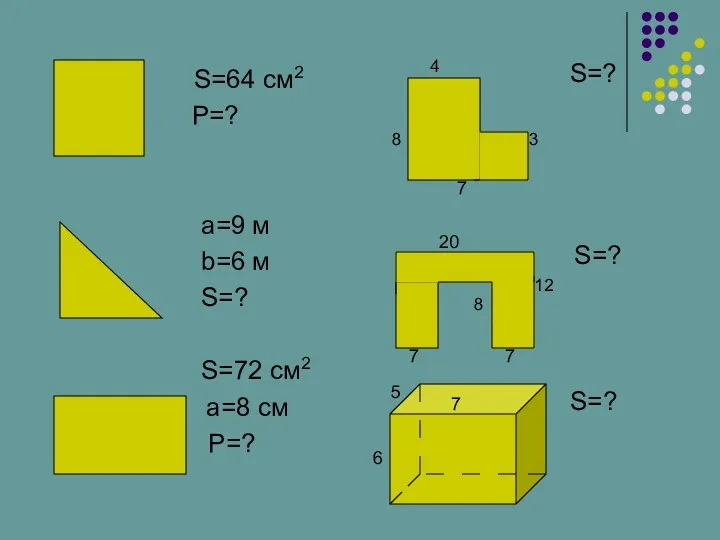 Урок в 5 классе :Площадь. Площадь прямоугольнина.
Урок в 5 классе :Площадь. Площадь прямоугольнина. Презентация к уроку по теме Радианная мера угла
Презентация к уроку по теме Радианная мера угла Уравнения в 5 классе
Уравнения в 5 классе