Содержание
- 2. Не каждому городу выпадает честь быть отмеченным в такой точной науке, как классическая математика. Кенигсберг же
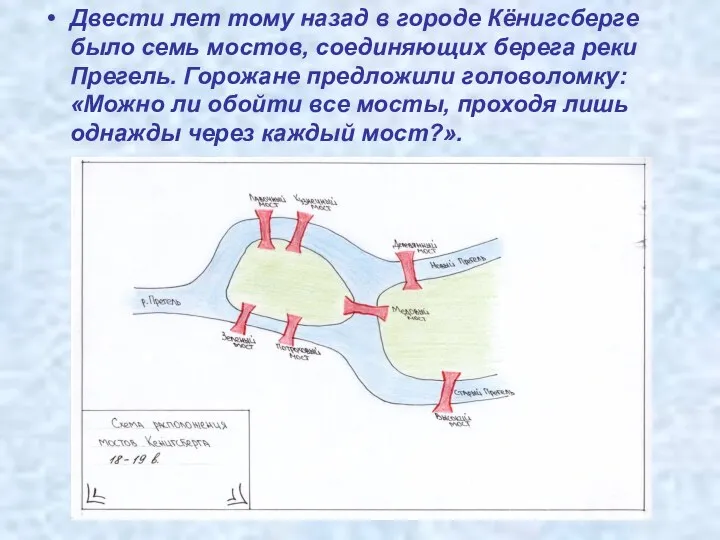
- 3. Двести лет тому назад в городе Кёнигсберге было семь мостов, соединяющих берега реки Прегель. Горожане предложили
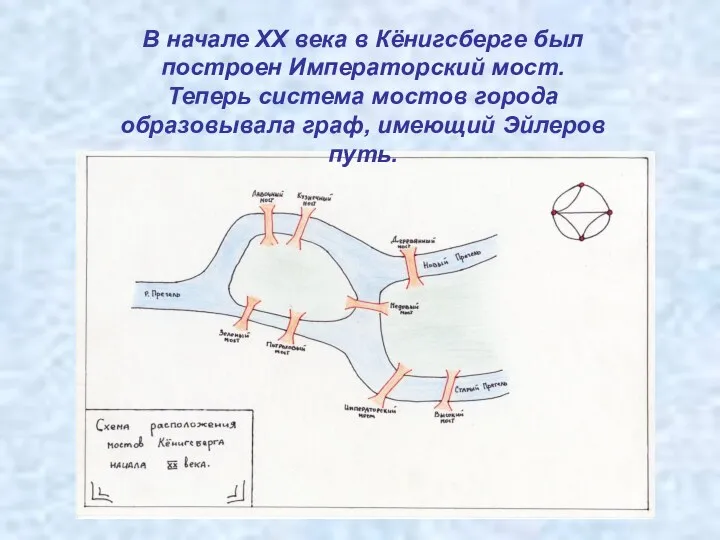
- 4. В начале XX века в Кёнигсберге был построен Императорский мост. Теперь система мостов города образовывала граф,
- 5. XX век опять изменил карту города. В 1945 году при бомбёжке города были разрушены многие мосты,
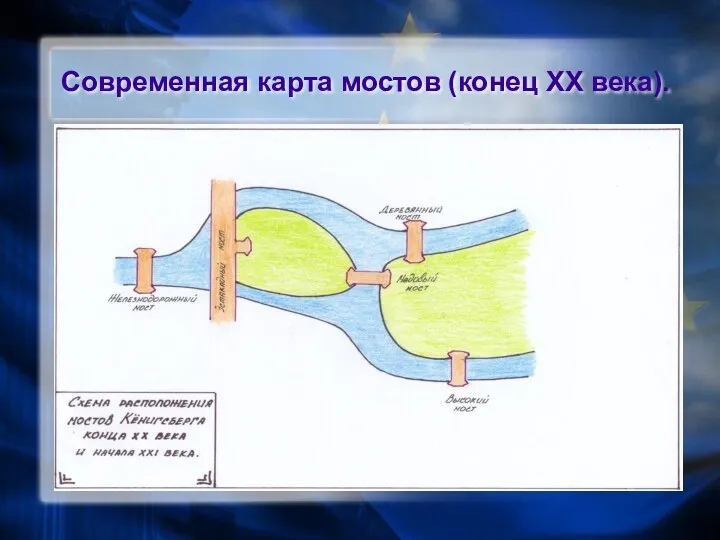
- 6. Современная карта мостов (конец XX века).
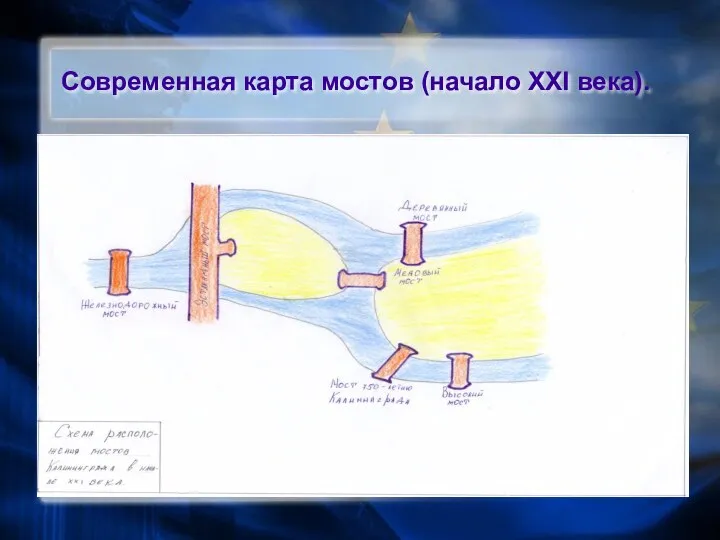
- 7. Современная карта мостов (начало XXI века).
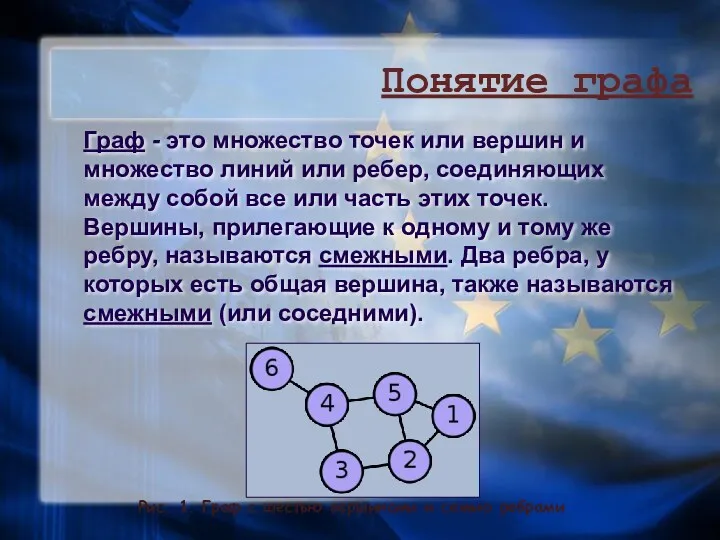
- 8. Граф - это множество точек или вершин и множество линий или ребер, соединяющих между собой все
- 9. Петля это дуга, начальная и конечная вершина которой совпадают. Пустым (нулевым)называется граф без ребер. Полным называется
- 10. Нулевой граф Граф, состоящий из «изолированных» вершин, называется нулевым графом Рис. 2. Нулевой граф
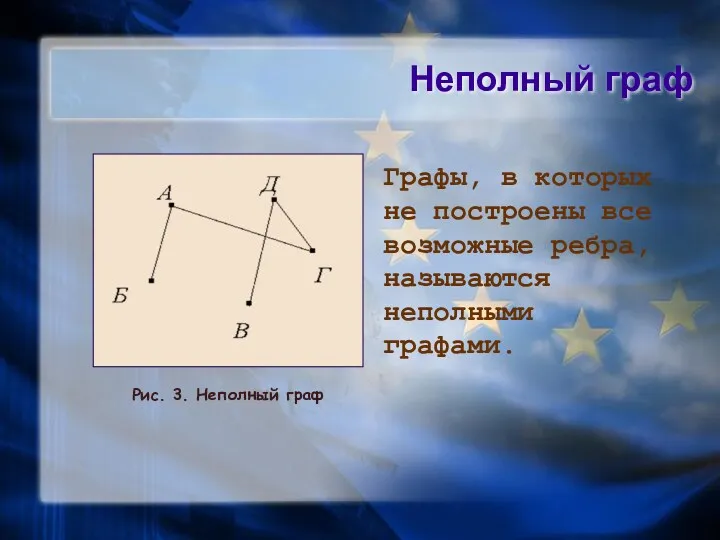
- 11. Неполный граф Графы, в которых не построены все возможные ребра, называются неполными графами. Рис. 3. Неполный
- 12. Степень графа Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень,
- 13. Заметим, что если полный граф имеет n вершин, то количество ребер равно n(n-1)/2 Задание 1. Существует
- 14. Построить полный граф, если известно что он содержит в себе 7 вершин. Составьте схему проведения розыгрыша
- 15. Теорема (Л. Эйлер, 1736 г.) Связный граф является эйлеровым тогда и только тогда, когда степени всех
- 16. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более
- 18. Скачать презентацию









 Интеллектуальная игра Колесо истории 6 класс
Интеллектуальная игра Колесо истории 6 класс Решение тригонометрических неравенств 10 класс ( профиль)
Решение тригонометрических неравенств 10 класс ( профиль) Урок в 5 классе по математике Округление чисел Анализ урока
Урок в 5 классе по математике Округление чисел Анализ урока Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства.
Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства. геометрическая прогрессия урок-презентация
геометрическая прогрессия урок-презентация конспект открытого урока по алгебре для 9 класса по теме Обобщающий урок по теме Арифметическая прогрессия
конспект открытого урока по алгебре для 9 класса по теме Обобщающий урок по теме Арифметическая прогрессия Производная и ее применение
Производная и ее применение Урок алгебры в 10 классе Преобразование тригонометрических выражений.
Урок алгебры в 10 классе Преобразование тригонометрических выражений. Целое уравнение и его корни
Целое уравнение и его корни Открытый урок по математике для 5 класса НОД и НОК
Открытый урок по математике для 5 класса НОД и НОК Эти увлекательные и познавательные задачи
Эти увлекательные и познавательные задачи Подготовка к ЕГЭ
Подготовка к ЕГЭ Теория вероятностей
Теория вероятностей презентация к уроку математики Действия с рациональными числами
презентация к уроку математики Действия с рациональными числами Презентация. Применение математической статистики в школе.
Презентация. Применение математической статистики в школе. презентация к уроку по математике Первообразная и интеграл
презентация к уроку по математике Первообразная и интеграл Урок по математике 6 класс по теме Пропорция
Урок по математике 6 класс по теме Пропорция Решение тригонометрических неравенств.
Решение тригонометрических неравенств. Исследовательская работа по теме Влияние математических действий на аликвоты
Исследовательская работа по теме Влияние математических действий на аликвоты Алгебраические дроби
Алгебраические дроби Презентация Мәйданнарны үлчәү берәмлекләре , 5 класс
Презентация Мәйданнарны үлчәү берәмлекләре , 5 класс Способы решения квадратных уравнений
Способы решения квадратных уравнений Решение уравнений и неравенств, содержащих модуль
Решение уравнений и неравенств, содержащих модуль Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Игра Кто хочет стать миллионером?
Игра Кто хочет стать миллионером? геометрическая прогрессия , 9 класс
геометрическая прогрессия , 9 класс Математик-бизнесмен
Математик-бизнесмен урок по математике и астрономии в 6 классе
урок по математике и астрономии в 6 классе