Базовые преобразования проекций, используемые при решении задач начертательной геометрии. (Лекция 6) презентация
Содержание
- 2. Базовые преобразования проекций, используемые при решении задач начертательной геометрии
- 3. Преобразование прямой общего положения в прямую уровня (построение дополнительной проекции прямой на плоскости проекций ей параллельной).
- 4. Практически рассматриваются всего два варианта преобразования. Вариант 1. Переход от общего положения объекта в параллельное положение
- 5. Базовая задача № 1. Построение дополнительной проекции прямой линии на параллельной ей плоскости проекций (Преобразование прямой
- 6. Задача решается на основе прямоуголь-ного варианта метода проецирования несколькими способами: Переменой плоскостей проекций - подбором дополнительной
- 7. Решение задачи способом перемены плоскостей проекций
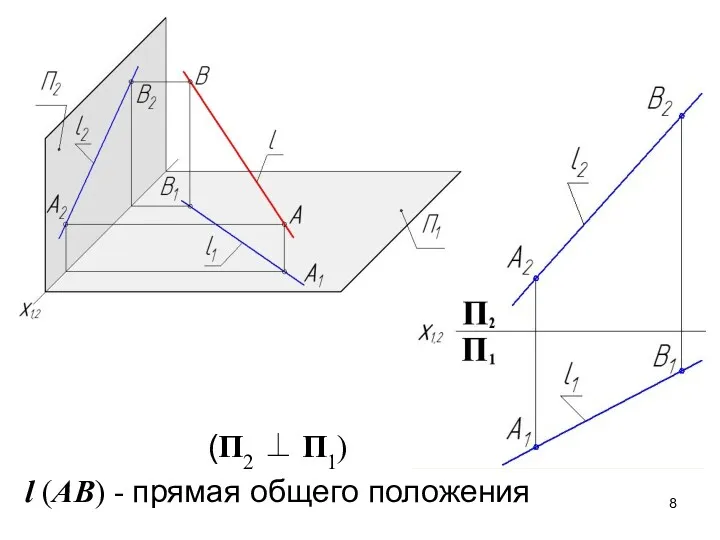
- 8. (П2 ⊥ П1) l (AB) - прямая общего положения
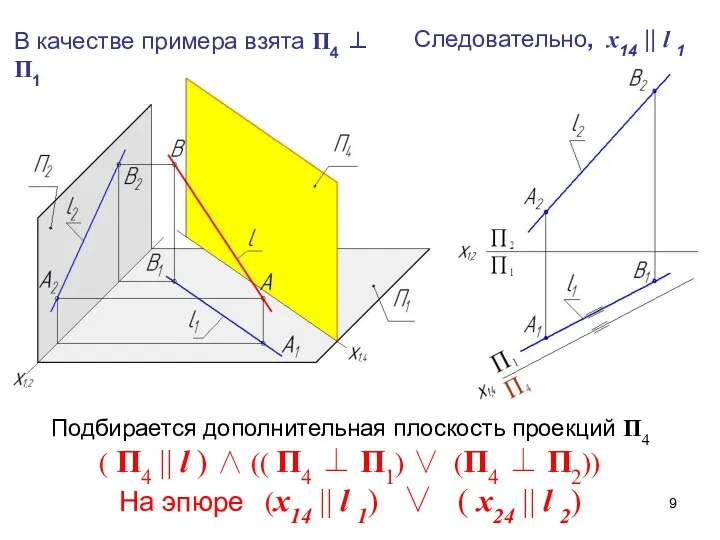
- 9. Подбирается дополнительная плоскость проекций П4 ( П4 || l ) ∧ (( П4 ⊥ П1) ∨
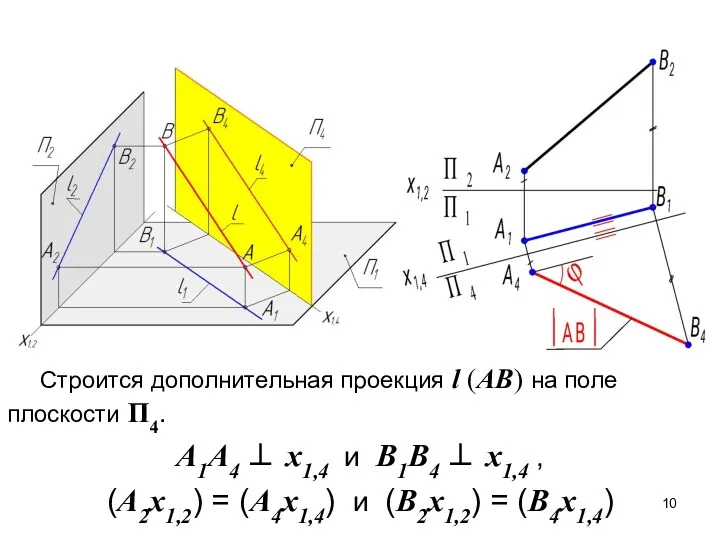
- 10. Строится дополнительная проекция l (AB) на поле плоскости П4. А1А4 ⊥ х1,4 и В1В4 ⊥ х1,4
- 11. Построение дополнительной проекции прямой линии в виде точки на основе дополнительного прямоугольного варианта способа проецирования –
- 12. При прямоугольном проецировании прямая явля-ется проецирующей, если она перпендикулярна пло-скости проекций. Следовательно, дополнительная плоскость проек-ций должна
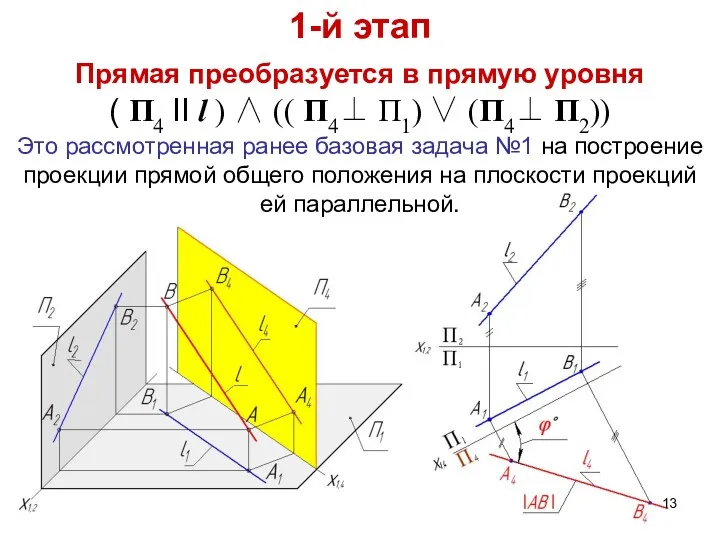
- 13. 1-й этап Прямая преобразуется в прямую уровня ( П4 II l ) ∧ (( П4⊥ П1)
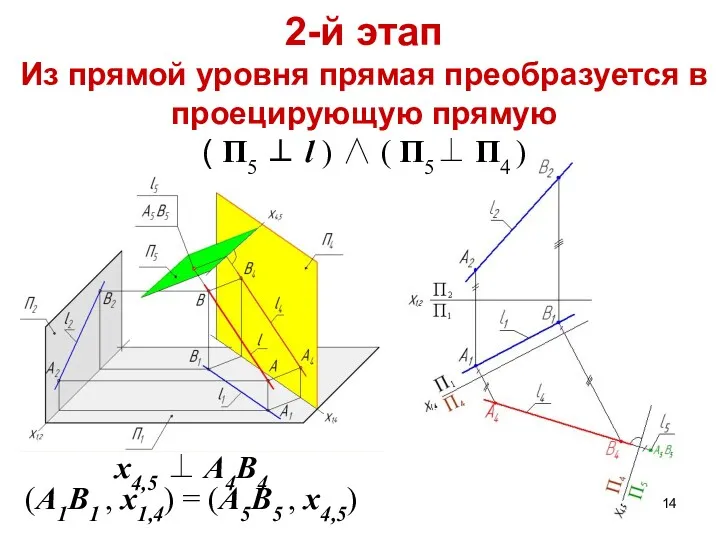
- 14. 2-й этап Из прямой уровня прямая преобразуется в проецирующую прямую ( П5 ⊥ l ) ∧
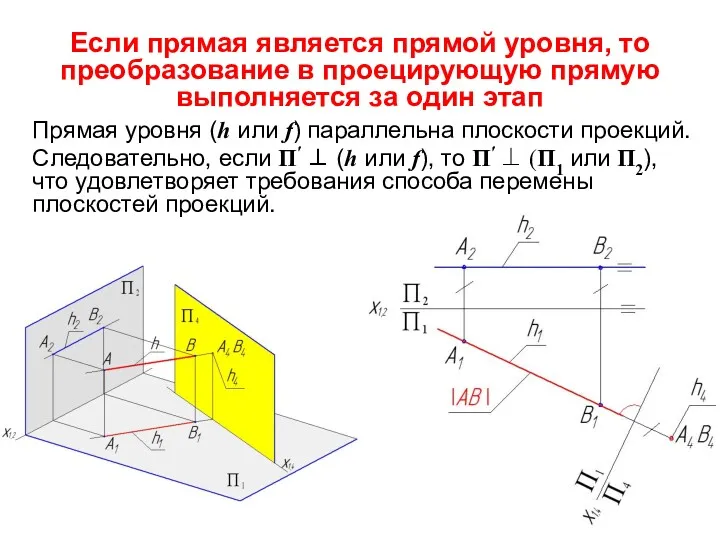
- 15. Если прямая является прямой уровня, то преобразование в проецирующую прямую выполняется за один этап Прямая уровня
- 16. Базовая задача № 3. Построение проекции плоскости в виде линии (Преобразование плоскости общего положения в проецирующую
- 17. Построение дополнительной проекции плоскости общего положения в виде прямой линии способом перемены (замены) плоскостей проекций
- 18. Так как данный способ преобразования основан на прямоугольном проецировании, то любая плоскость, например Т, является проецирующей,
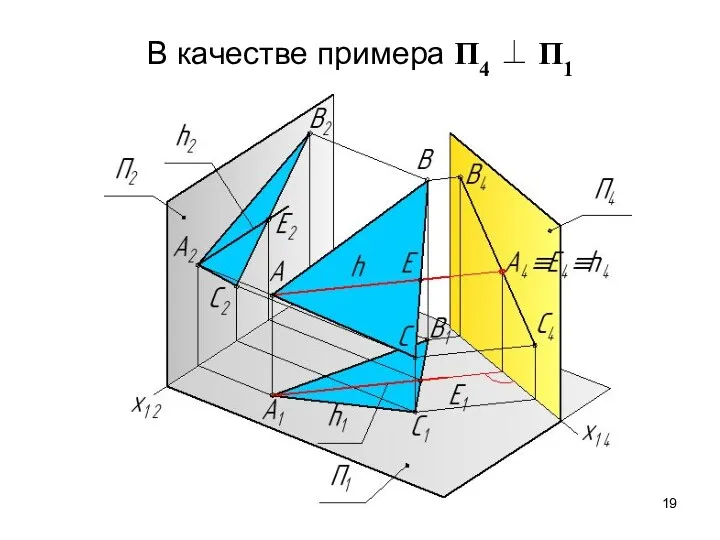
- 19. В качестве примера П4 ⊥ П1
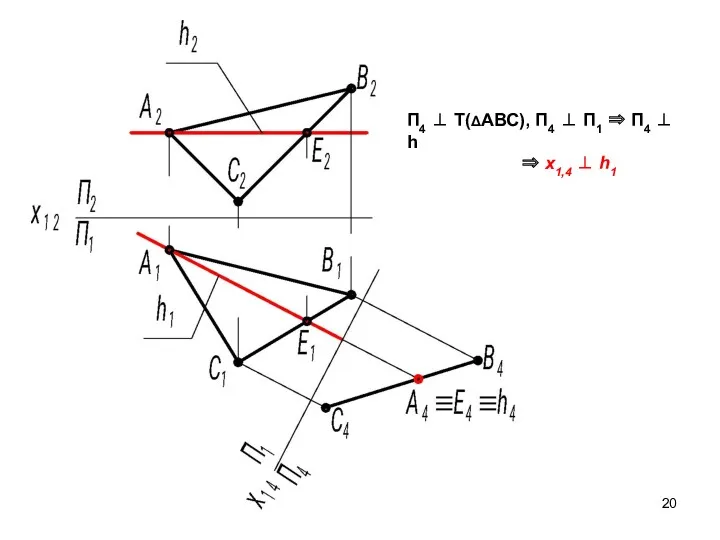
- 20. П4 ⊥ Т(ΔАВС), П4 ⊥ П1 ⇒ П4 ⊥ h ⇒ х1,4 ⊥ h1
- 21. Базовая задача № 4. Построение проекции плоской фигуры на плоскости проекций ей параллельной
- 22. Решение задачи способом перемены (замены) плоскостей проекций
- 23. П′ II Т Так как плоскость Т – плоскость общего положения, то любая плоскость ей параллельная,
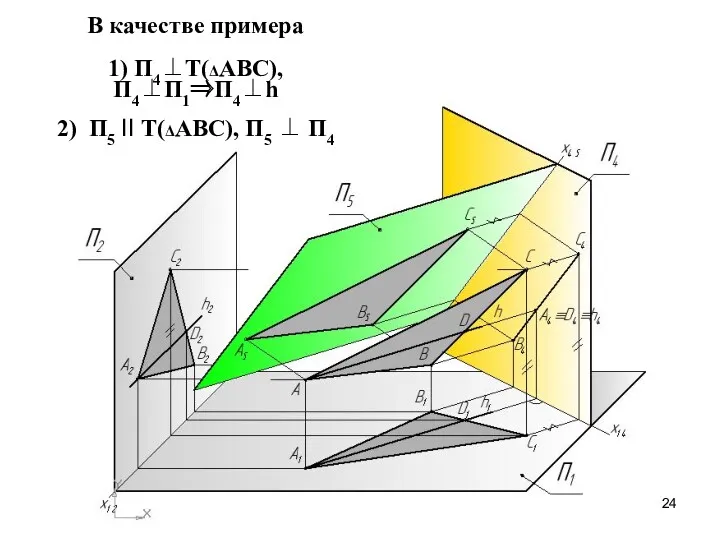
- 24. В качестве примера 1) П4⊥Т(ΔАВС), П4⊥П1⇒П4⊥h 2) П5 II Т(ΔАВС), П5 ⊥ П4
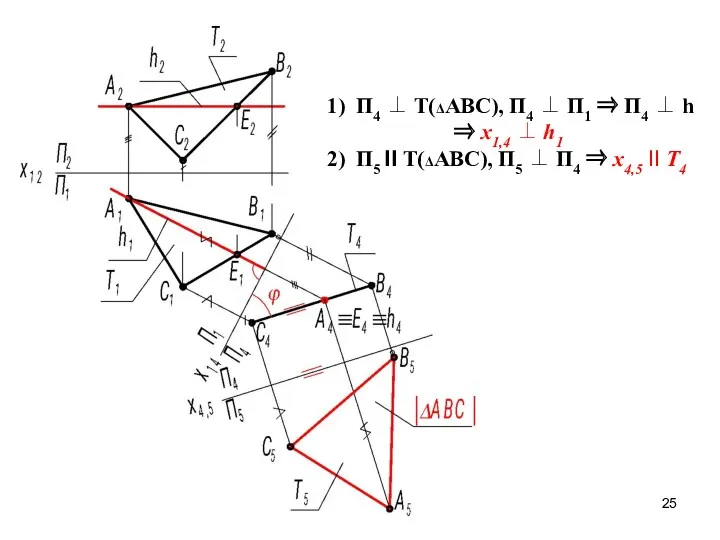
- 25. 1) П4 ⊥ Т(ΔАВС), П4 ⊥ П1 ⇒ П4 ⊥ h ⇒ х1,4 ⊥ h1 2)
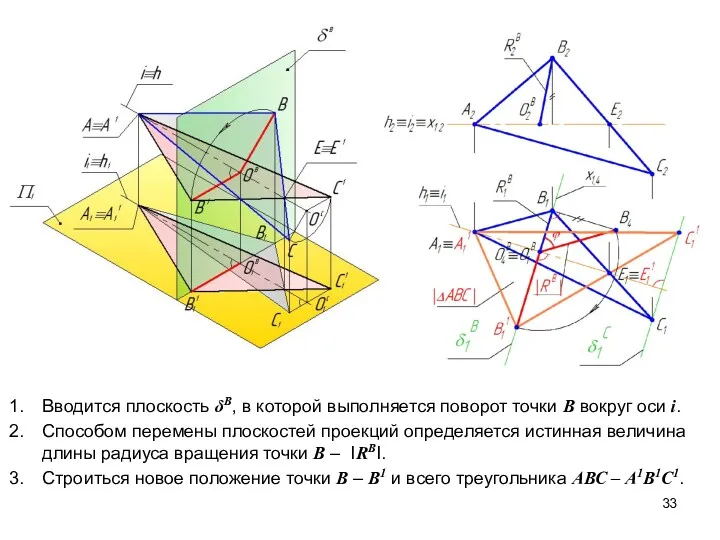
- 26. Решение задачи способом вращения вокруг прямой уровня
- 27. В ходе решения задачи плоская фигура должна быть повернута вокруг оси, являющейся прямой уровня плоскости, в
- 28. В представленном далее примере в качестве оси вращения взята горизонталь. Следовательно, заданная фигура должна быть повернута
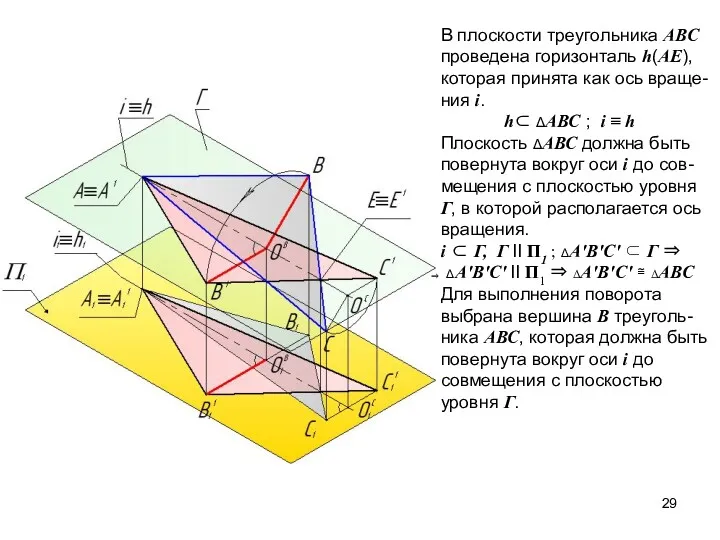
- 29. В плоскости треугольника АВС проведена горизонталь h(АЕ), которая принята как ось враще- ния i. h⊂ ΔАВС
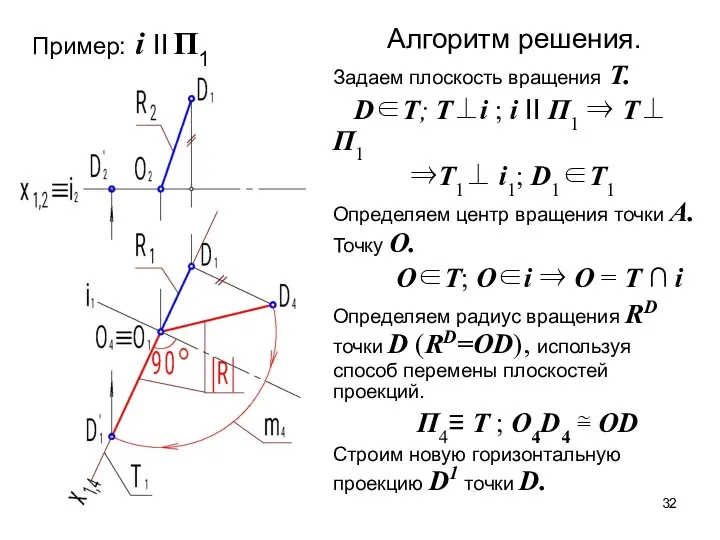
- 30. Вспомним рассмотренный ранее метод поворота точки вокруг прямой уровня
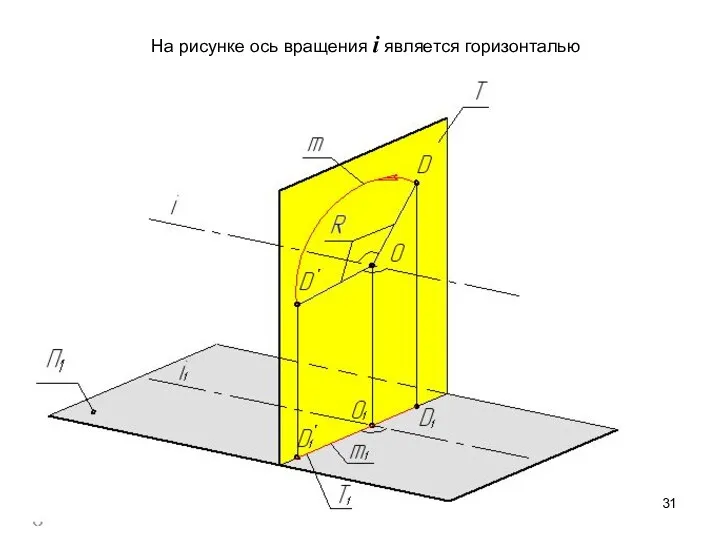
- 31. На рисунке ось вращения i является горизонталью
- 32. Алгоритм решения. Задаем плоскость вращения T. D∈Т; Т⊥i ; i II П1 ⇒ Т⊥ П1 ⇒Т1⊥
- 33. Вводится плоскость δВ, в которой выполняется поворот точки В вокруг оси i. Способом перемены плоскостей проекций
- 34. Решение задачи способом совмещения плоскости общего положения с какой-либо плоскостью проекций (вращение вокруг следа плоскости)
- 35. Вспомним рассмотренный ранее метод совмещения плоскости общего положения с плоскостью проекций путем ее поворота вокруг следа
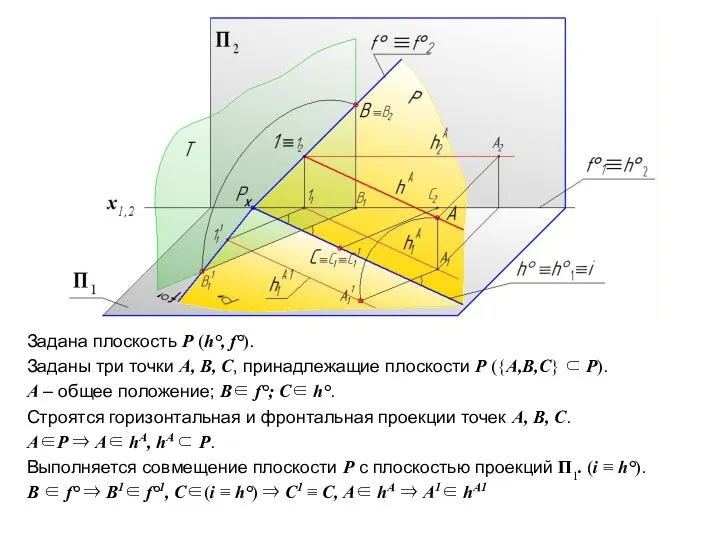
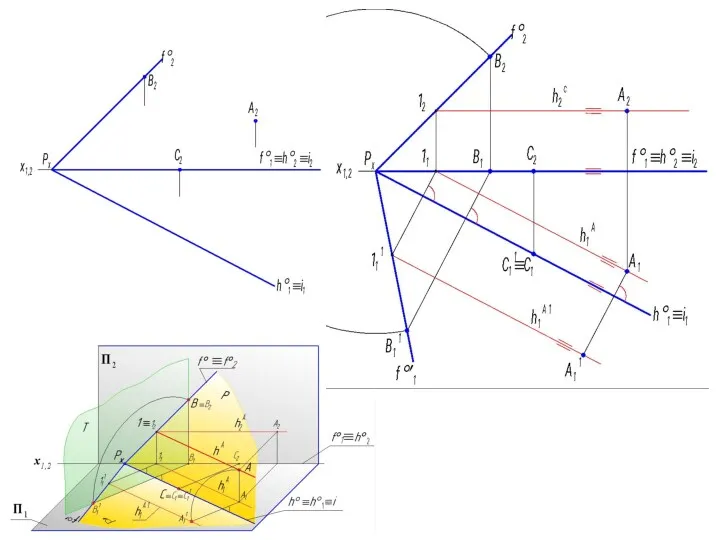
- 36. Пример. Совместить плоскость Р(h0, f0 ) с горизонтальной плоскостью проекций П1 поворотом вокруг горизонтали h0. Задаем
- 37. Задана плоскость Р (h°, f°). Заданы три точки А, В, С, принадлежащие плоскости Р ({А,В,С} ⊂
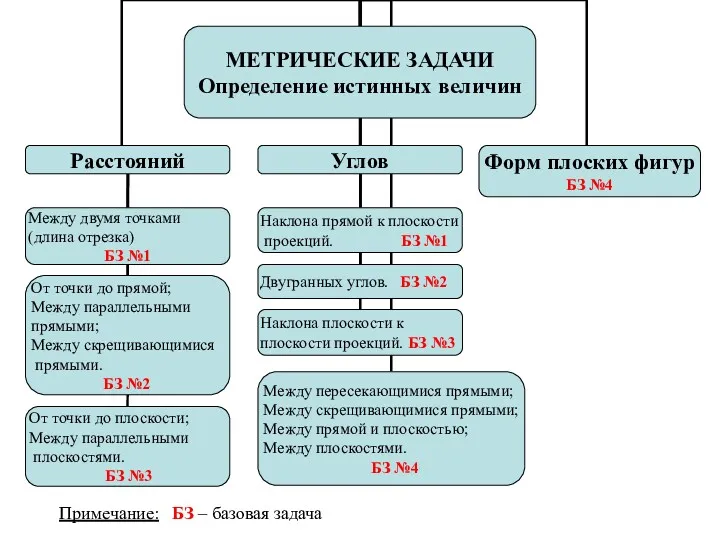
- 39. Метрические задачи
- 40. Метрическими называются задачи, в ходе решения которых определяется значение измеряемой величины – расстояния между двумя точками
- 41. Примечание: БЗ – базовая задача
- 43. Скачать презентацию























 Графическая работа. Рисунок технический
Графическая работа. Рисунок технический Правила оформления чертежей
Правила оформления чертежей Способы преобразования проекций (Лекция 3)
Способы преобразования проекций (Лекция 3) Разрез (урок черчения в 9 классе)
Разрез (урок черчения в 9 классе) Положение прямой относительно плоскостей проекций
Положение прямой относительно плоскостей проекций Правила нанесения размеров с учетом формы предмета
Правила нанесения размеров с учетом формы предмета Сборочные чертежи. Соединения деталей
Сборочные чертежи. Соединения деталей Многогранники и их виды. Графические модели многогранников. (Лекция 5)
Многогранники и их виды. Графические модели многогранников. (Лекция 5) Нарезание резьбы
Нарезание резьбы Сборочные чертежи
Сборочные чертежи Геометрические параметры деталей. Основные понятия
Геометрические параметры деталей. Основные понятия Линии чертежа. Чертежный шрифт
Линии чертежа. Чертежный шрифт Разработка мобильного комплекта полигонного оборудования
Разработка мобильного комплекта полигонного оборудования Сечения, разрезы ЕСКД ГОСТ 2.305-68
Сечения, разрезы ЕСКД ГОСТ 2.305-68 Угловая перспектива
Угловая перспектива Правила, стандарты оформления чертежей по ЕСКД
Правила, стандарты оформления чертежей по ЕСКД Рисунок технический
Рисунок технический Аксонометрическая проекция окружности
Аксонометрическая проекция окружности Наглядное изображение втулки
Наглядное изображение втулки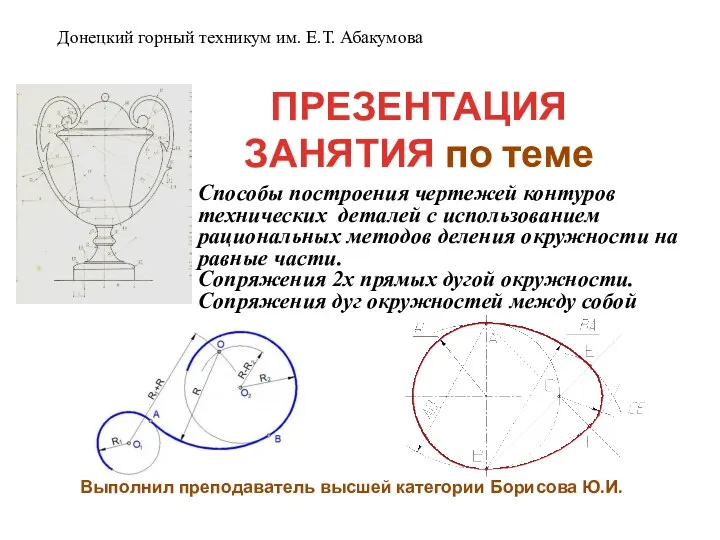 Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части
Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части Конструкторские документы. Чертеж общего вида и сборочный чертеж
Конструкторские документы. Чертеж общего вида и сборочный чертеж Взаимное пересечение кривых поверхностей
Взаимное пересечение кривых поверхностей Последовательность чтения сборочных чертежей
Последовательность чтения сборочных чертежей Форматы. Масштабы. Шрифты
Форматы. Масштабы. Шрифты Основные проекционные методы построения чертежей. Лекция 1
Основные проекционные методы построения чертежей. Лекция 1 Правила разработки, оформления и выпуска конструкторской документации
Правила разработки, оформления и выпуска конструкторской документации Чертежи. (Вариант 1-25)
Чертежи. (Вариант 1-25) 10_1_Сварка
10_1_Сварка