Содержание
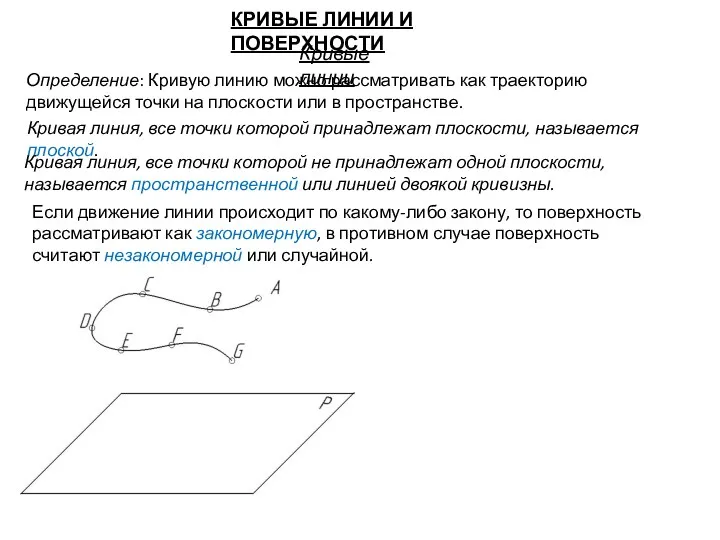
- 2. КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ Кривые линии Определение: Кривую линию можно рассматривать как траекторию движущейся точки на
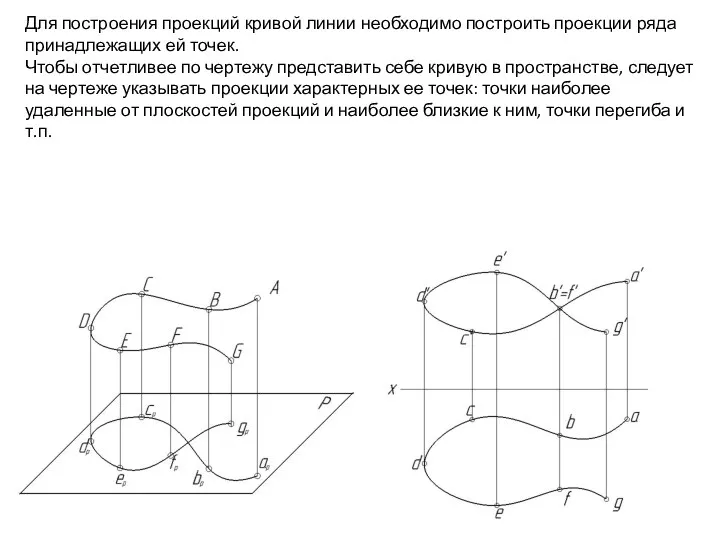
- 3. Для построения проекций кривой линии необходимо построить проекции ряда принадлежащих ей точек. Чтобы отчетливее по чертежу
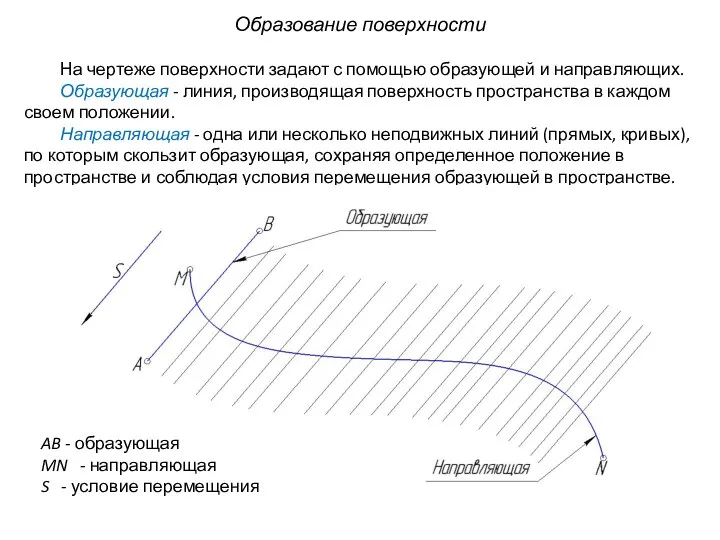
- 4. Образование поверхности На чертеже поверхности задают с помощью образующей и направляющих. Образующая - линия, производящая поверхность
- 5. Классификация поверхностей По типу образующей: линейчатые – образующая прямая линия (цилиндр, конус); нелинейчатые - образующая кривая
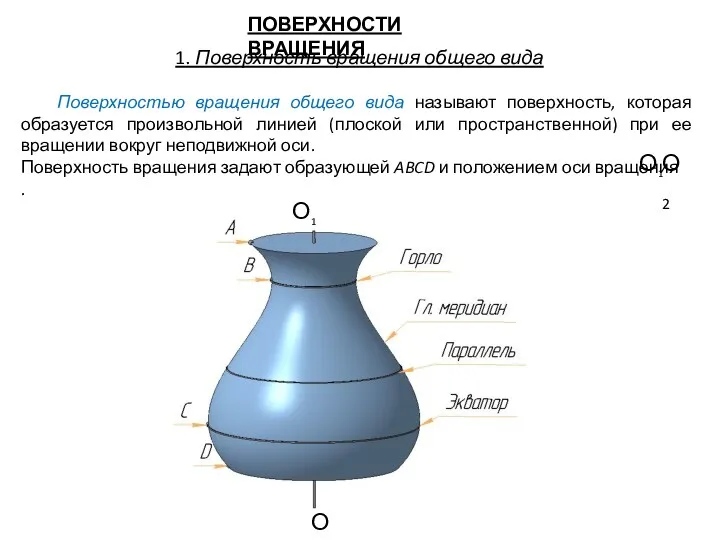
- 6. ПОВЕРХНОСТИ ВРАЩЕНИЯ 1. Поверхность вращения общего вида Поверхностью вращения общего вида называют поверхность, которая образуется произвольной
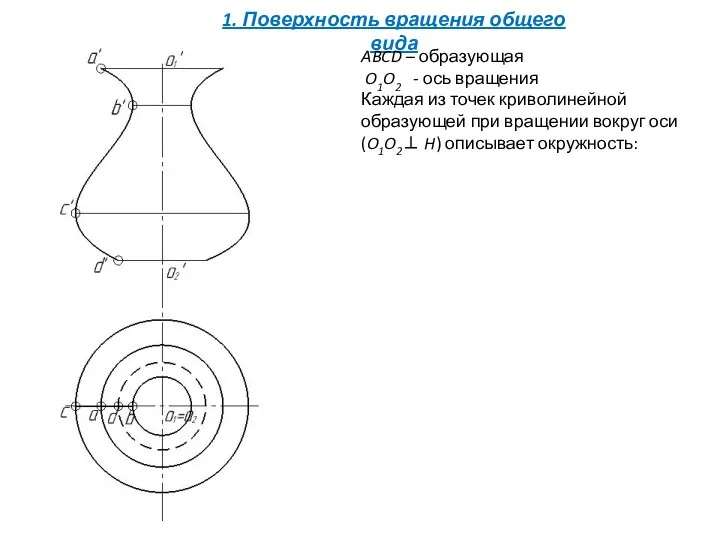
- 7. 1. Поверхность вращения общего вида ABCD – образующая O1O2 - ось вращения
- 8. 1. Поверхность вращения общего вида ABCD – образующая O1O2 - ось вращения Каждая из точек криволинейной
- 9. ABCD – образующая O1O2 - ось вращения Каждая из точек криволинейной образующей при вращении вокруг оси
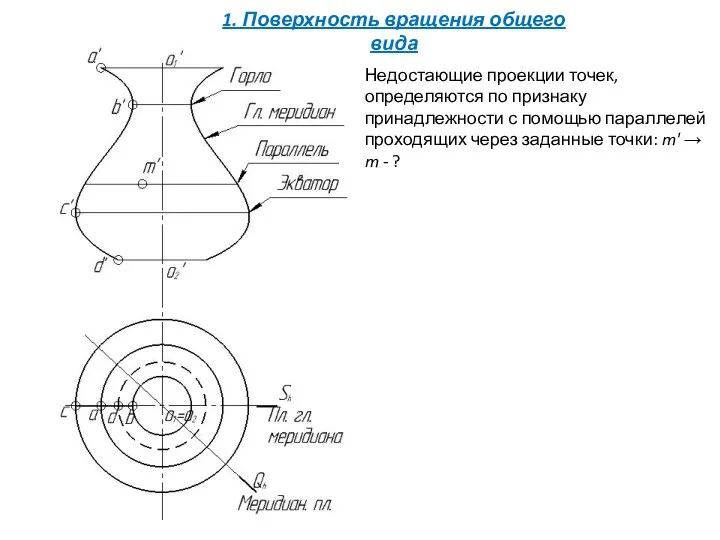
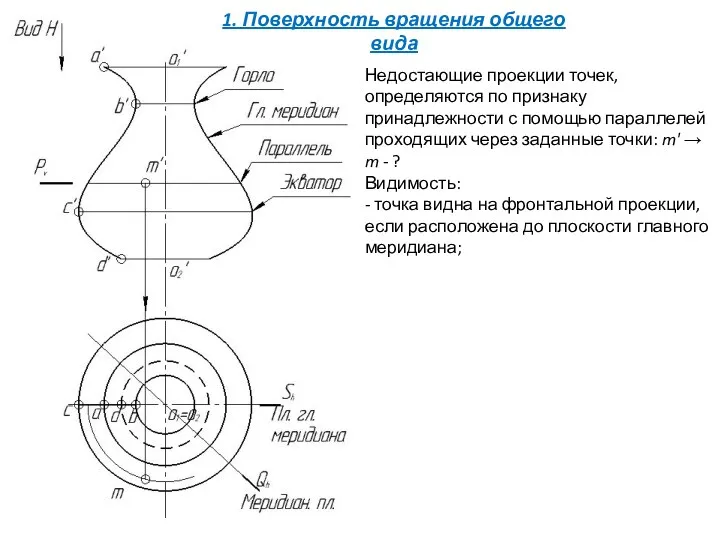
- 10. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 11. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
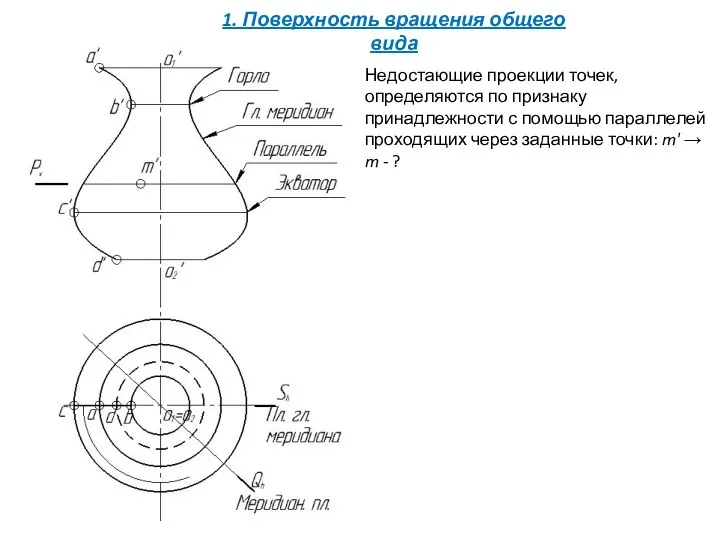
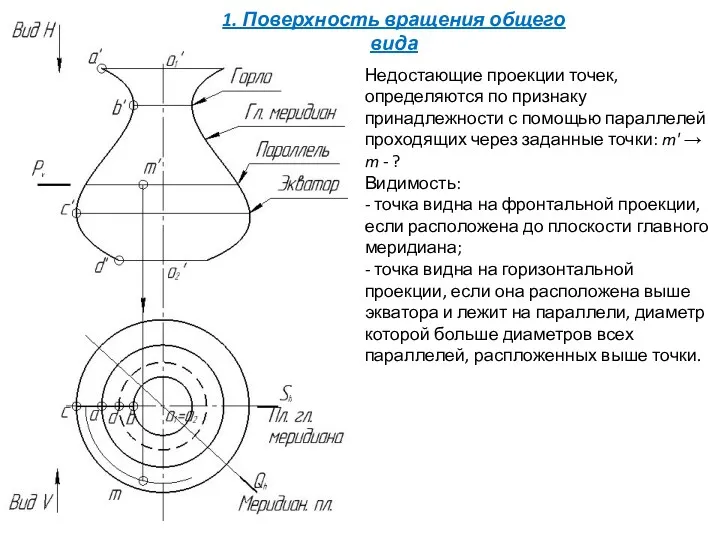
- 12. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
- 13. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
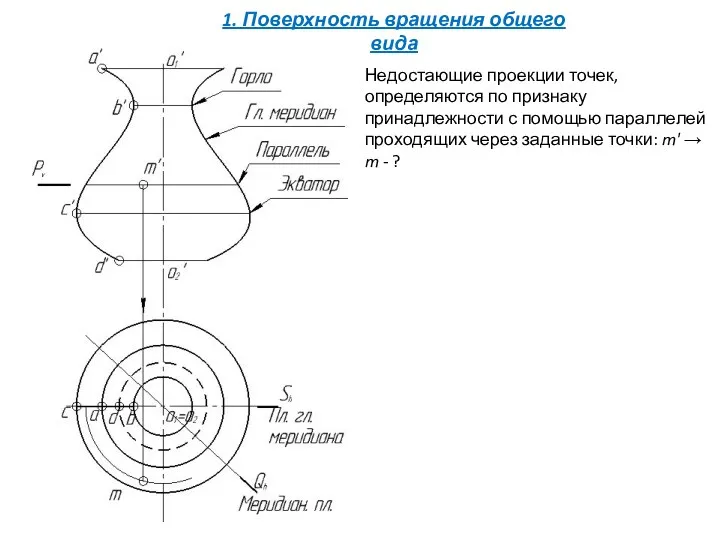
- 14. Недостающие проекции точек, определяются по признаку принадлежности с помощью параллелей проходящих через заданные точки: m' →
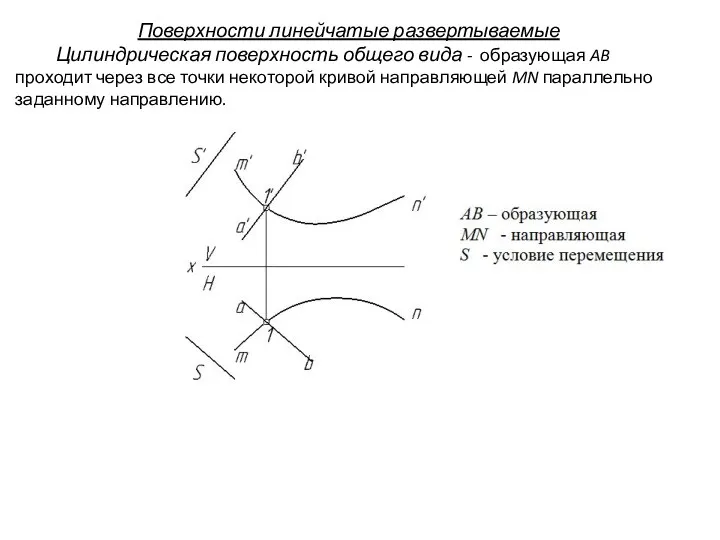
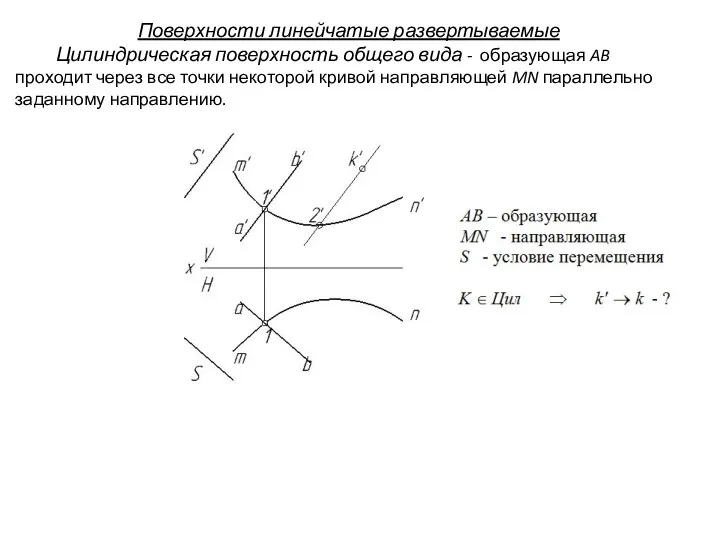
- 15. Поверхности линейчатые развертываемые Цилиндрическая поверхность общего вида - образующая AB проходит через все точки некоторой кривой
- 16. Поверхности линейчатые развертываемые Цилиндрическая поверхность общего вида - образующая AB проходит через все точки некоторой кривой
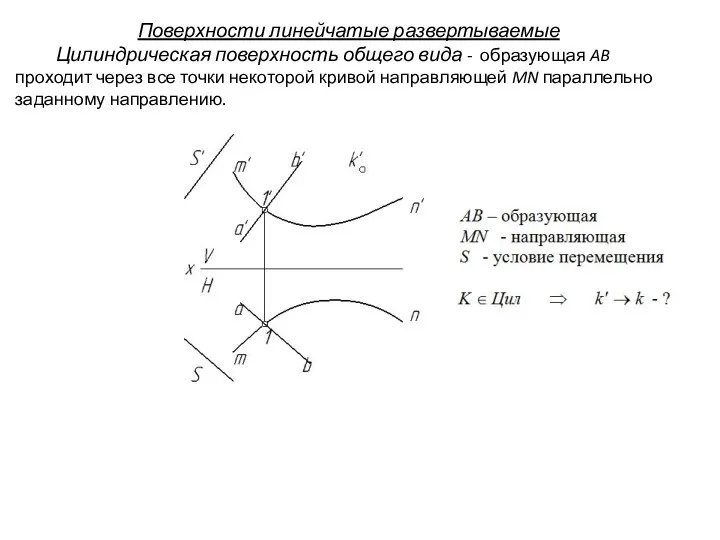
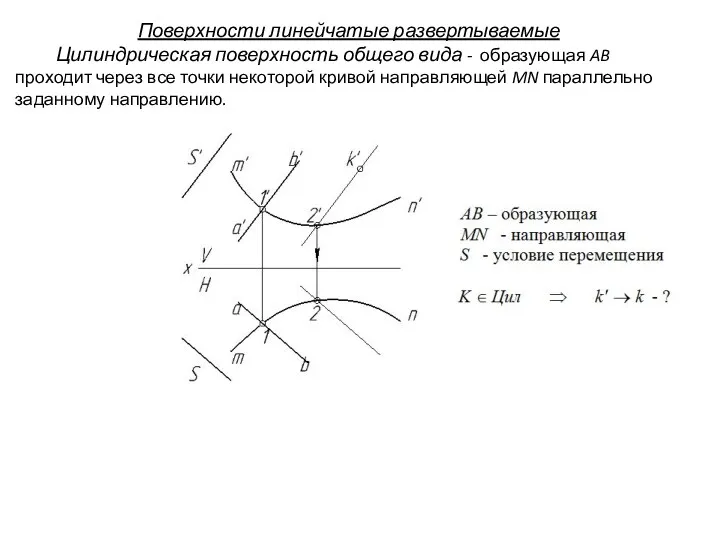
- 17. Поверхности линейчатые развертываемые Цилиндрическая поверхность общего вида - образующая AB проходит через все точки некоторой кривой
- 18. Поверхности линейчатые развертываемые Цилиндрическая поверхность общего вида - образующая AB проходит через все точки некоторой кривой
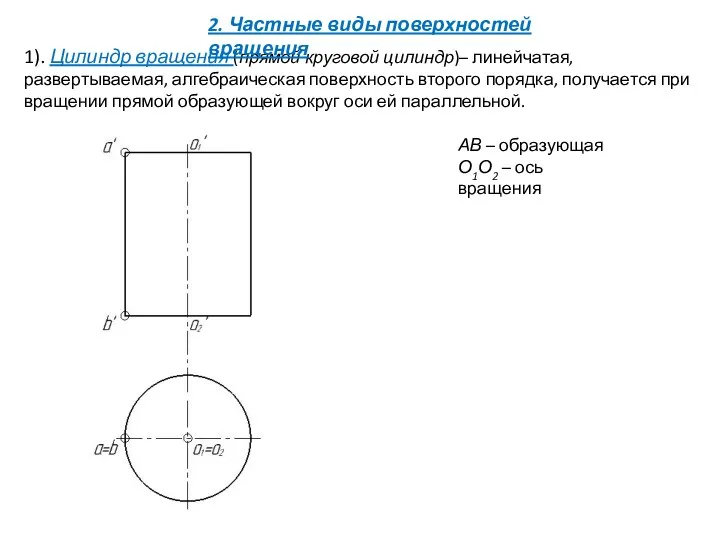
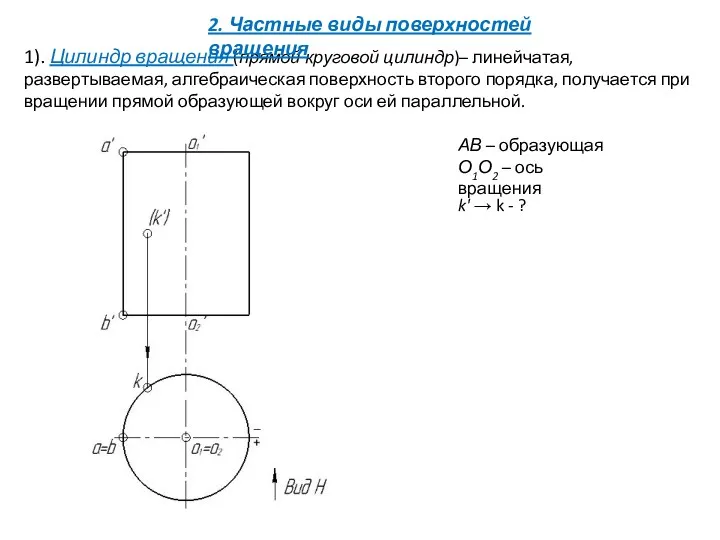
- 19. 2. Частные виды поверхностей вращения 1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая, алгебраическая поверхность второго
- 20. 1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой
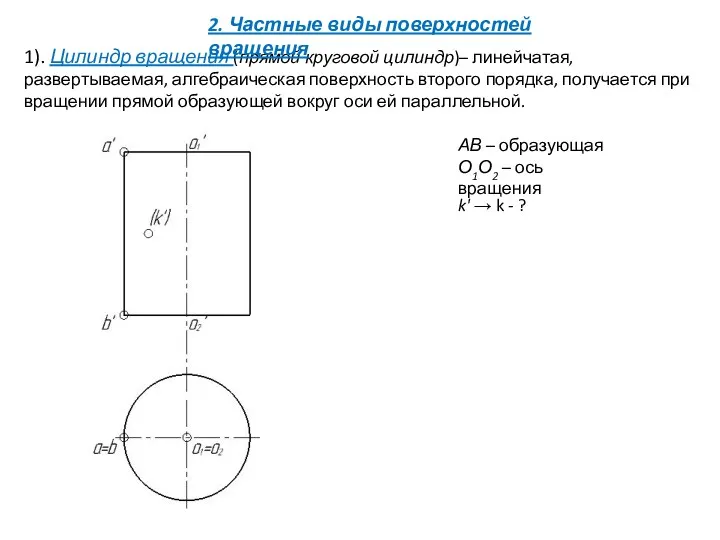
- 21. 1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой
- 22. 1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой
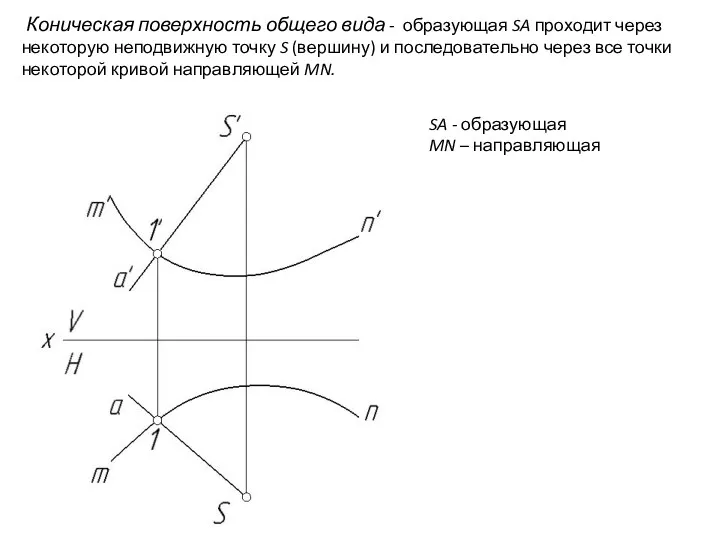
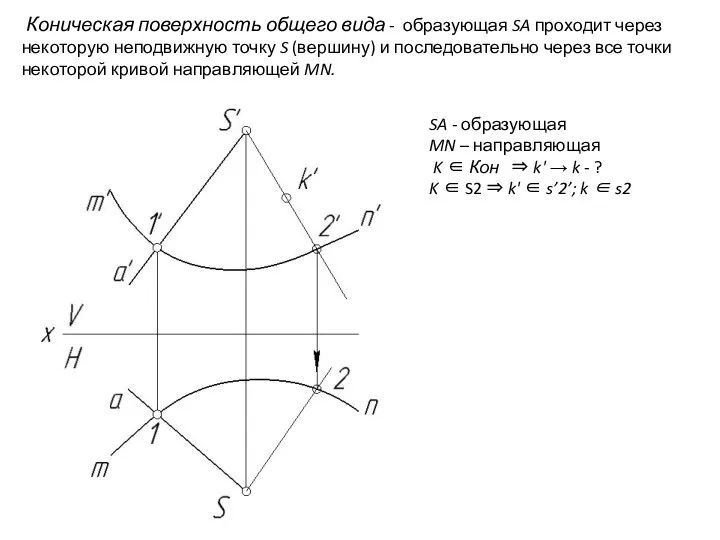
- 23. Коническая поверхность общего вида - образующая SA проходит через некоторую неподвижную точку S (вершину) и последовательно
- 24. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? Коническая
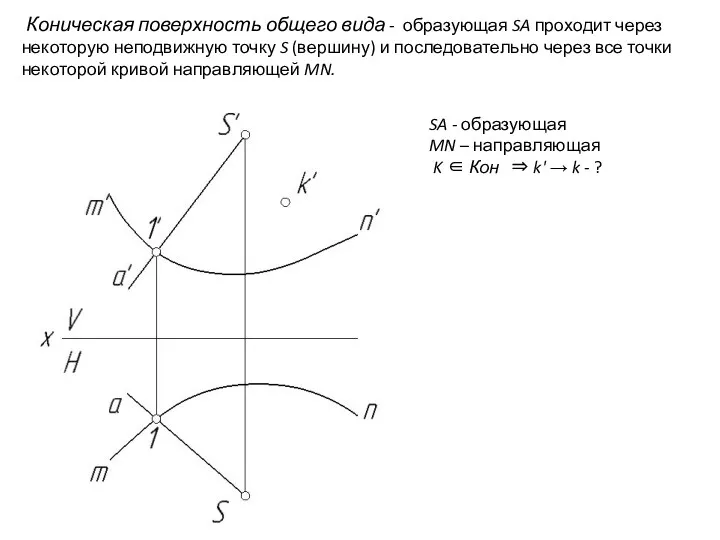
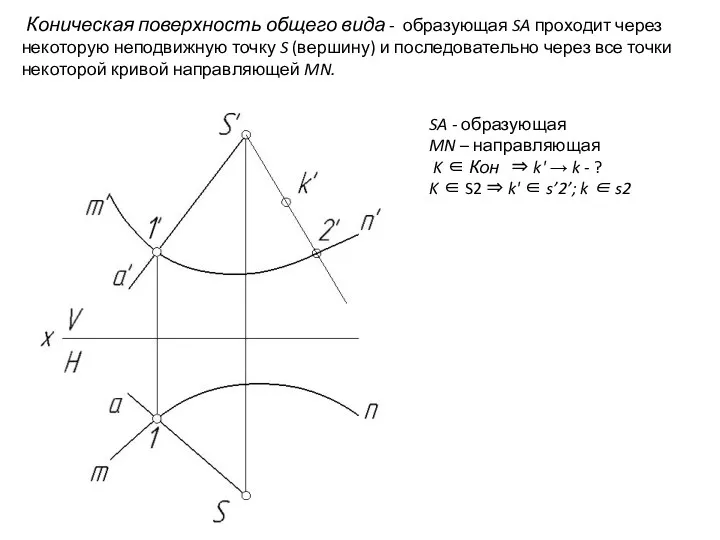
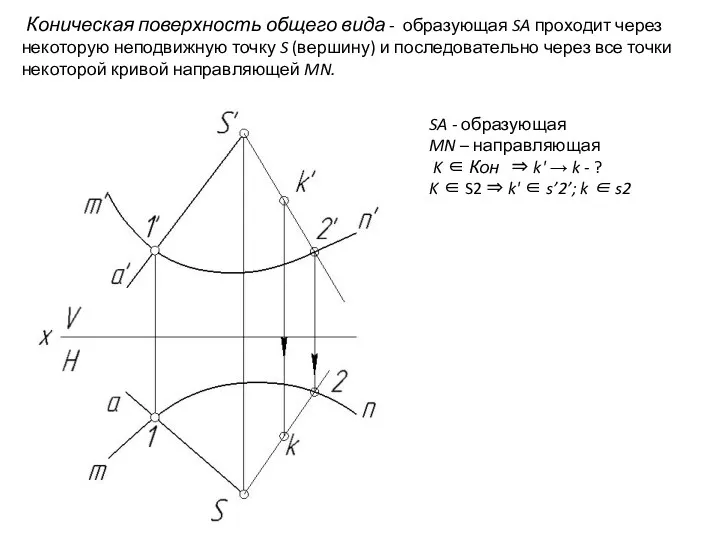
- 25. Коническая поверхность общего вида - образующая SA проходит через некоторую неподвижную точку S (вершину) и последовательно
- 26. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? K
- 27. SA - образующая MN – направляющая K ∈ Кон ⇒ k' → k - ? K
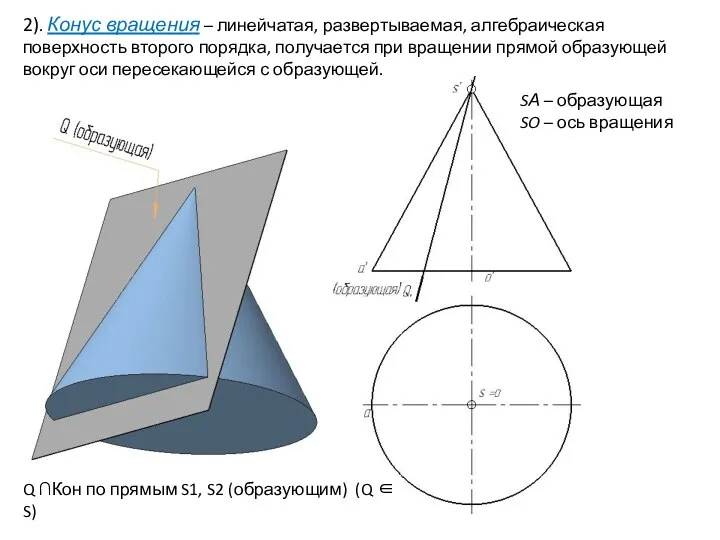
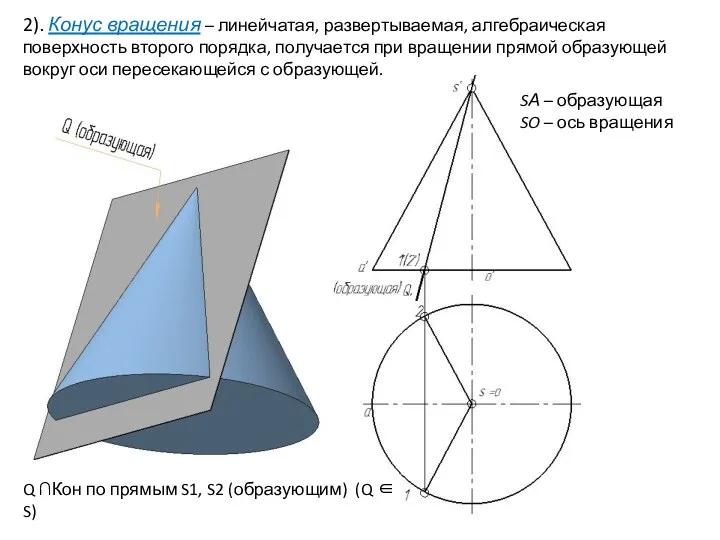
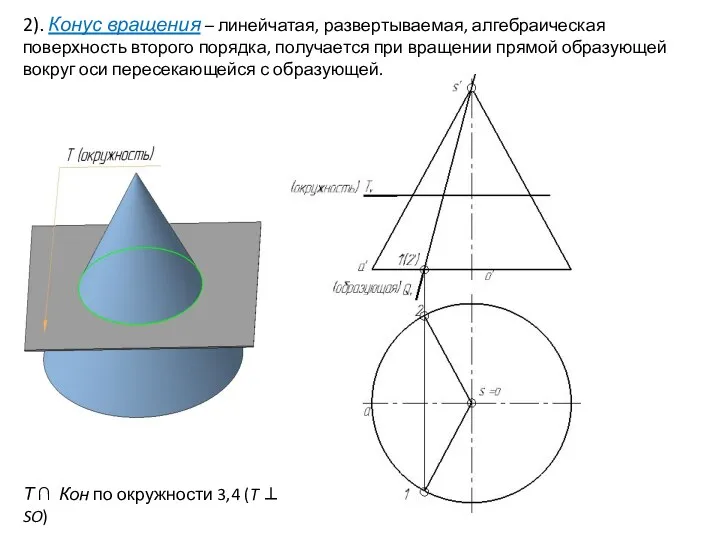
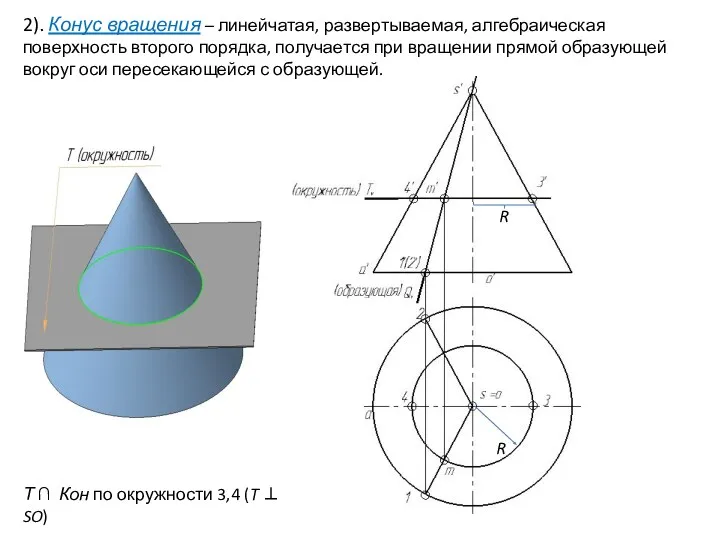
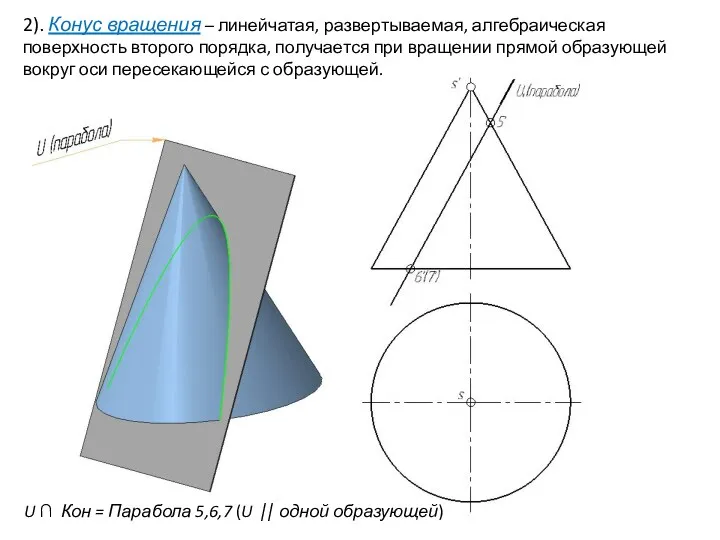
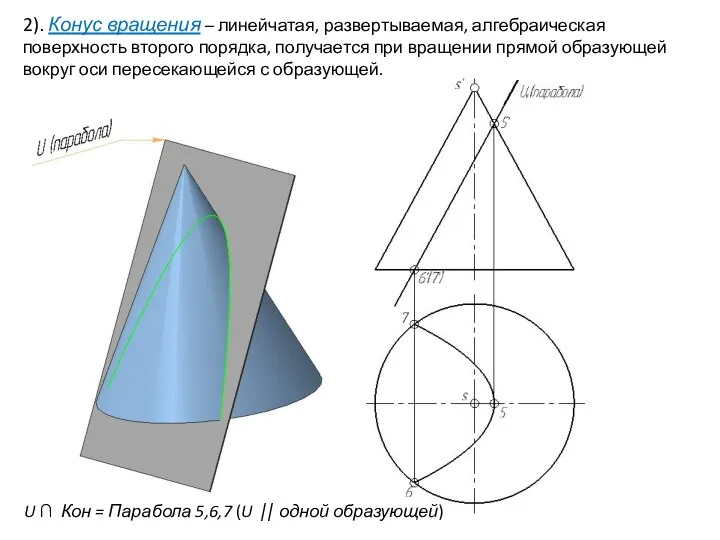
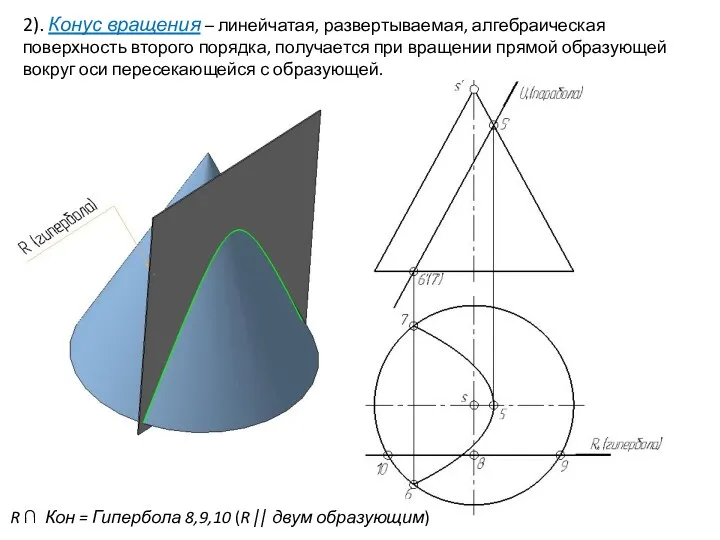
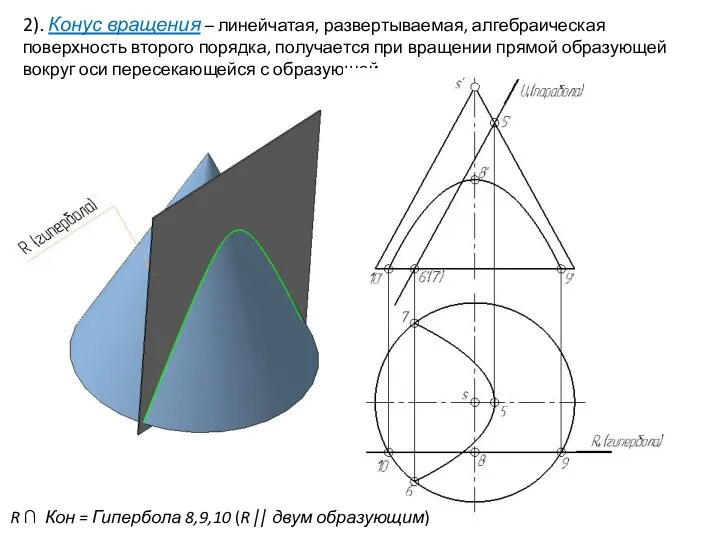
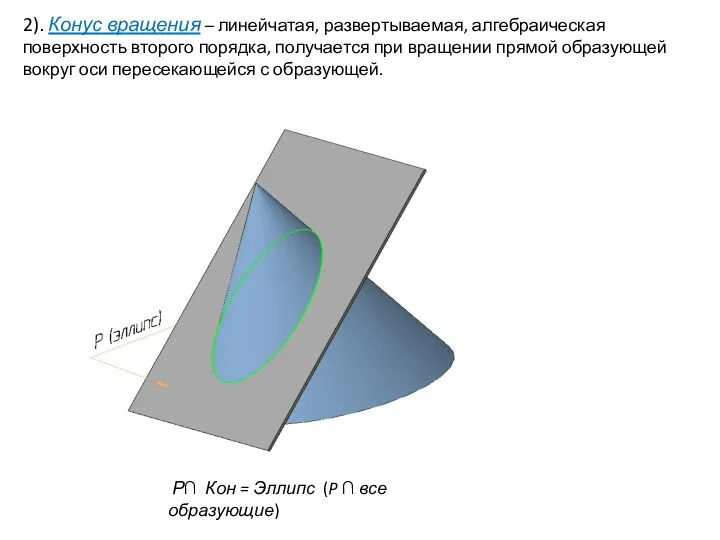
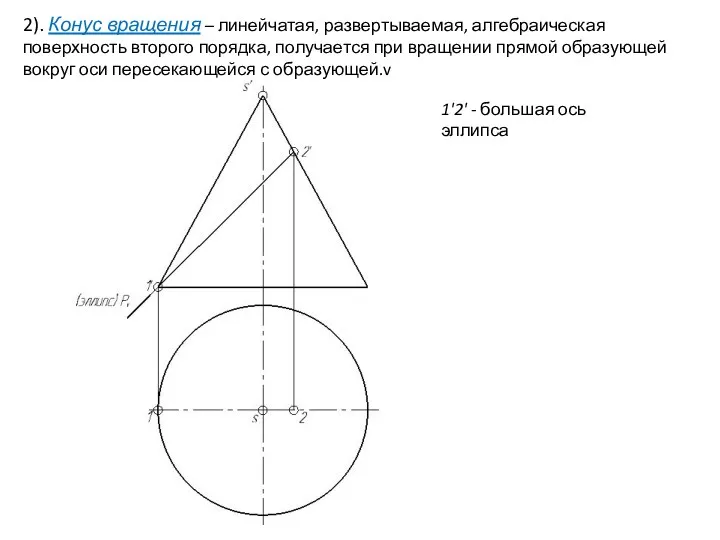
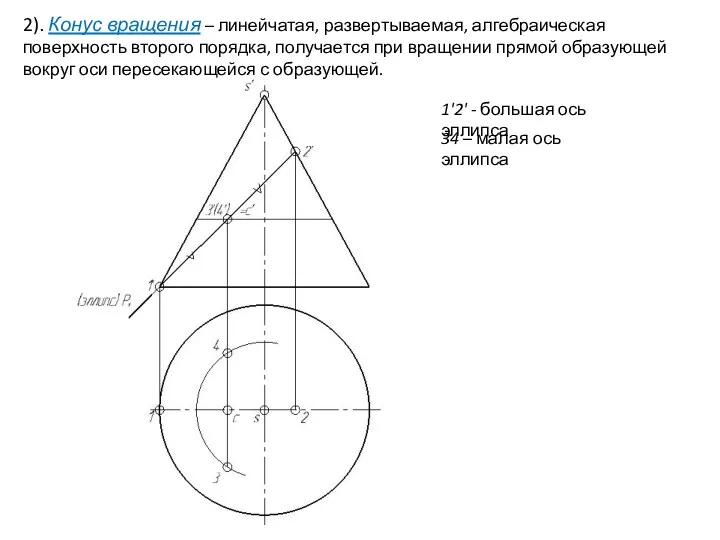
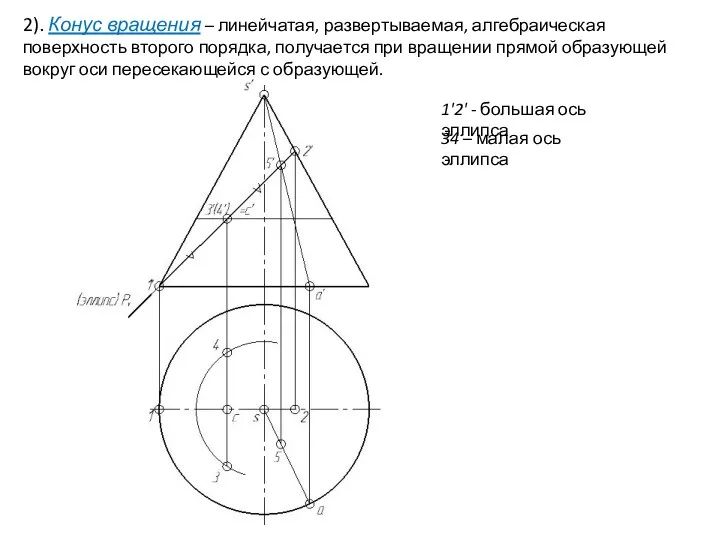
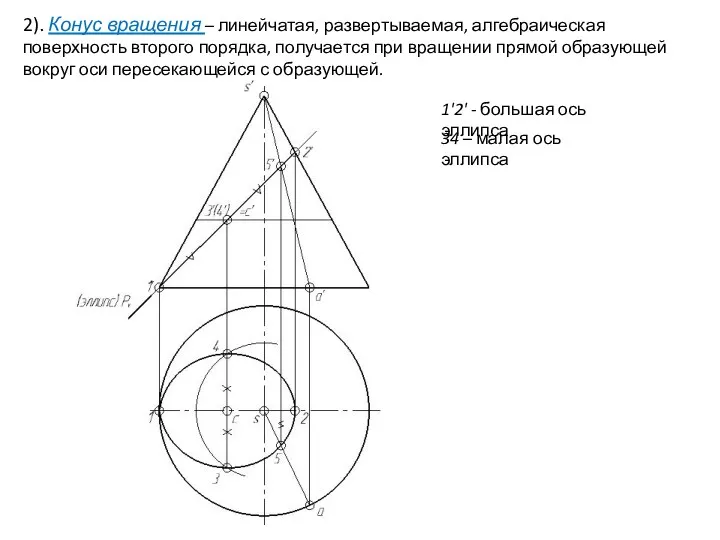
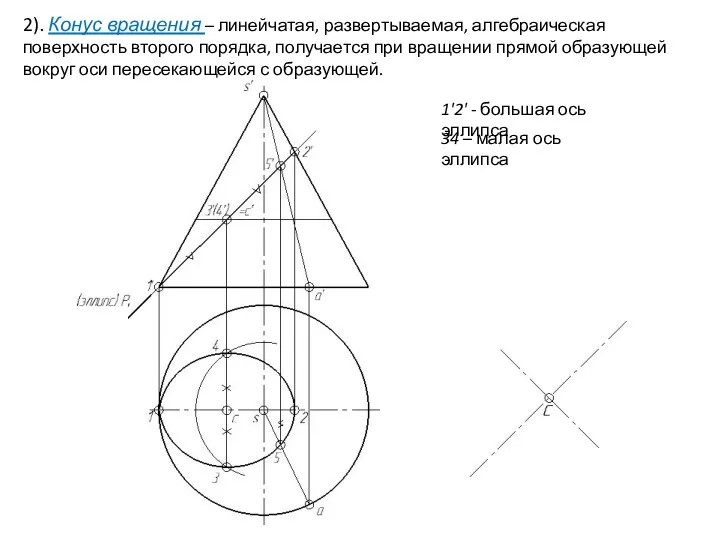
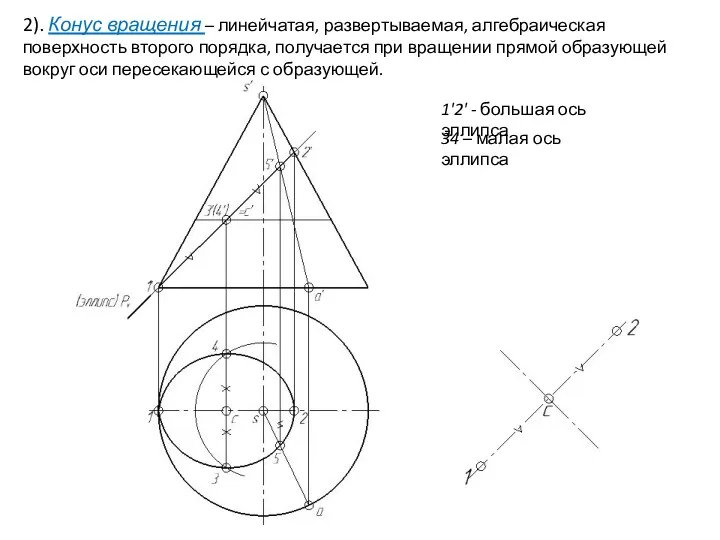
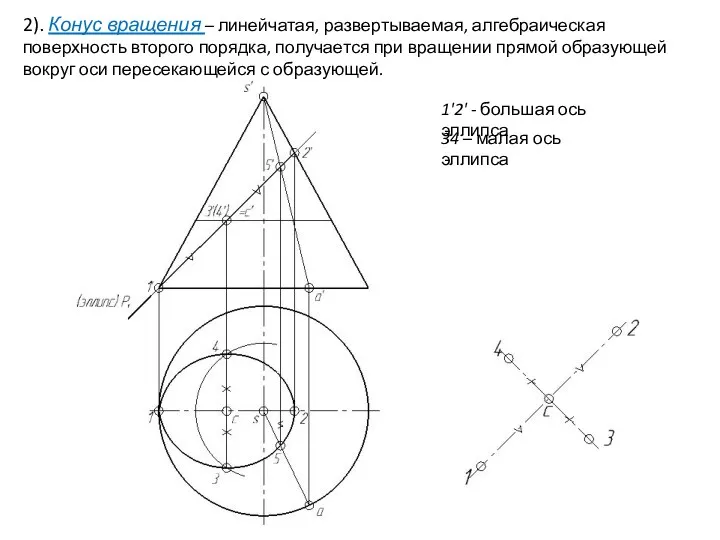
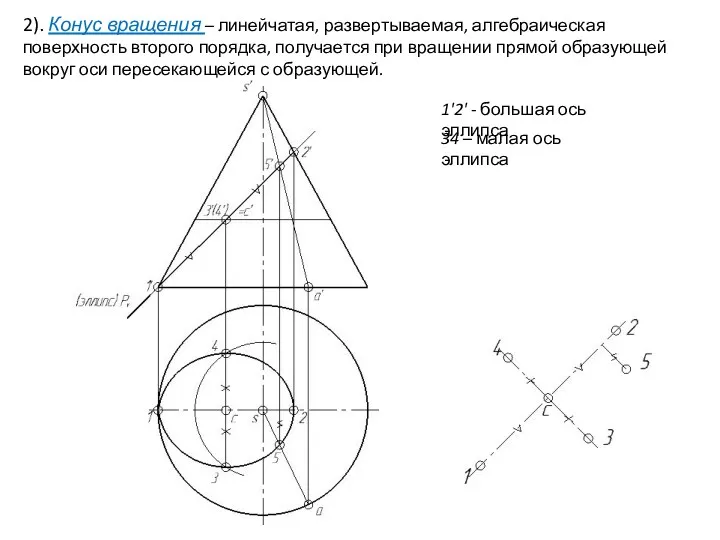
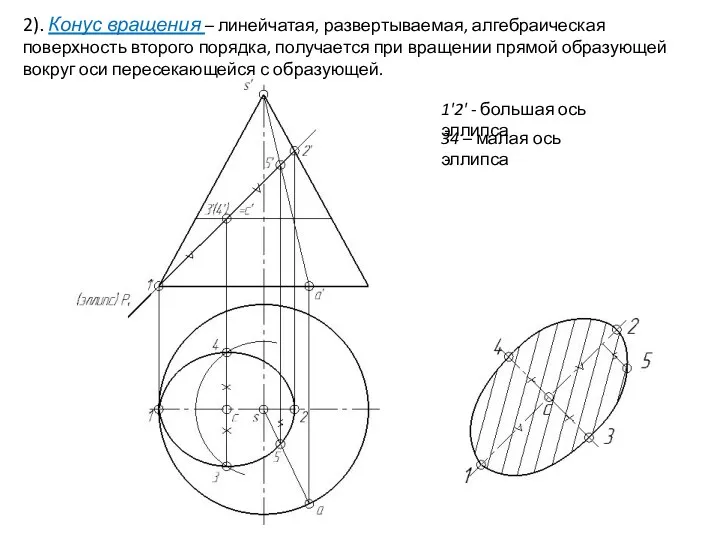
- 28. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 29. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 30. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 31. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 32. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 33. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 34. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 35. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 36. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 37. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 38. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 39. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 40. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 41. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 42. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 43. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 44. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
- 45. 2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхность второго порядка, получается при вращении прямой образующей вокруг
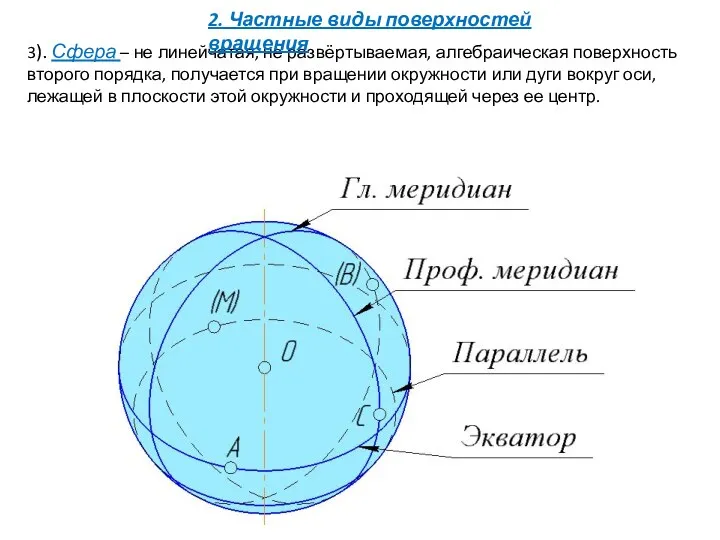
- 46. 3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго порядка, получается при вращении окружности или
- 47. 2. Частные виды поверхностей вращения 3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго порядка,
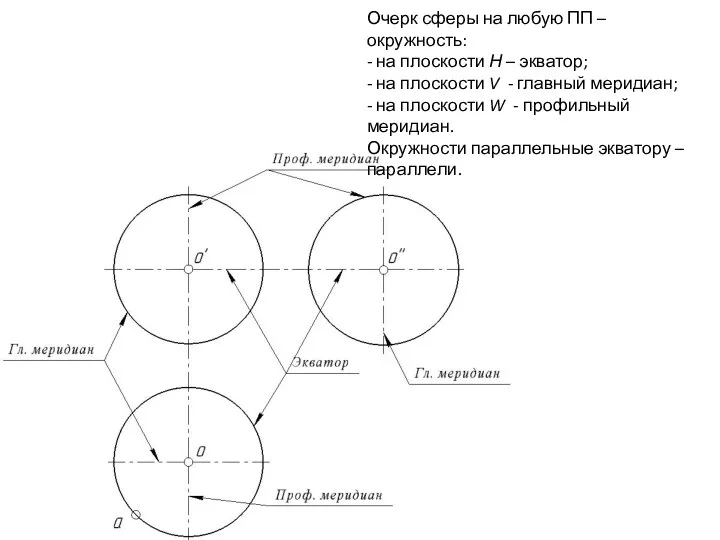
- 48. Очерк сферы на любую ПП – окружность: - на плоскости Н – экватор; - на плоскости
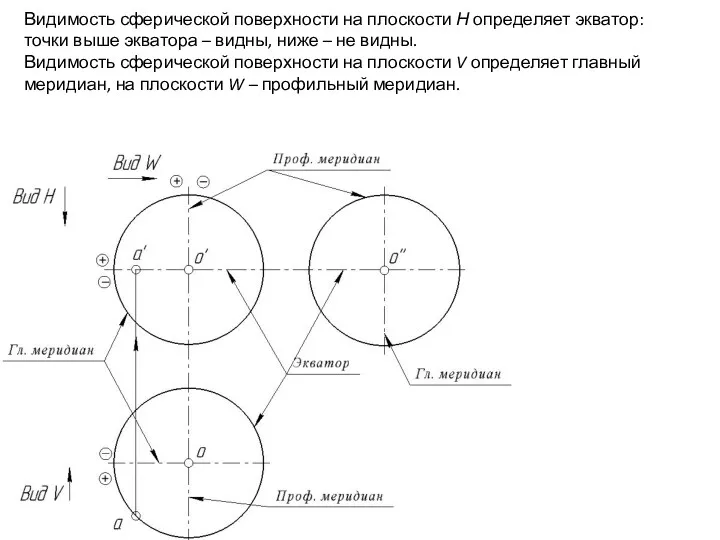
- 49. Видимость сферической поверхности на плоскости Н определяет экватор: точки выше экватора – видны, ниже – не
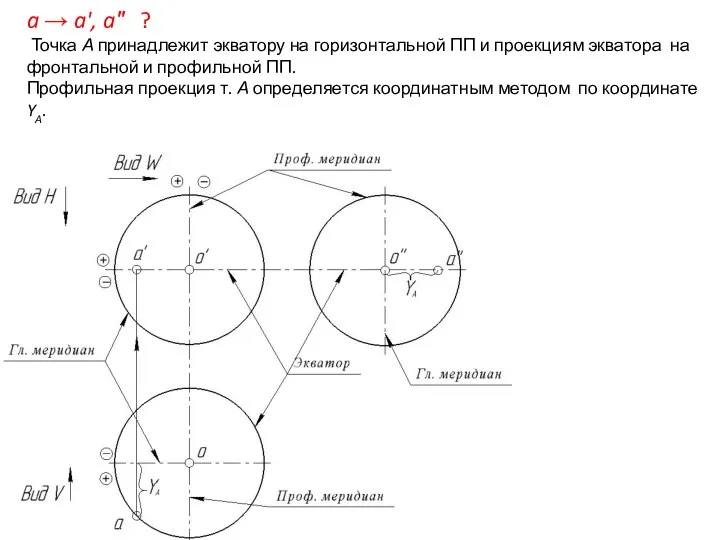
- 50. a → a', a″ ? Точка А принадлежит экватору на горизонтальной ПП и проекциям экватора на
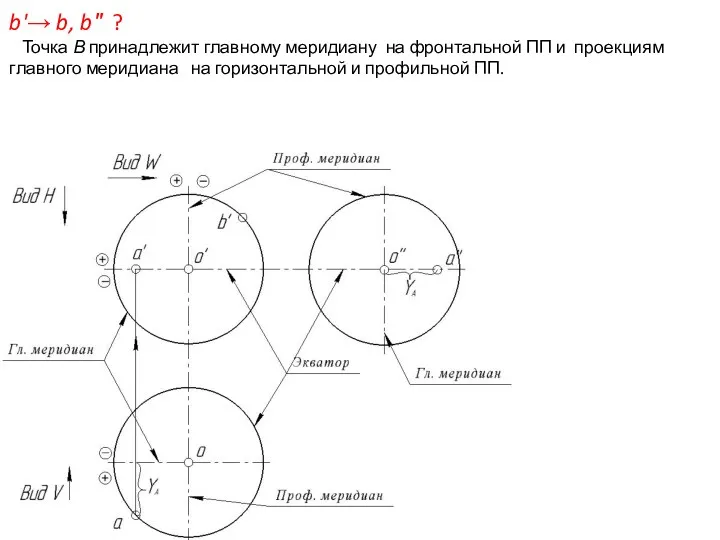
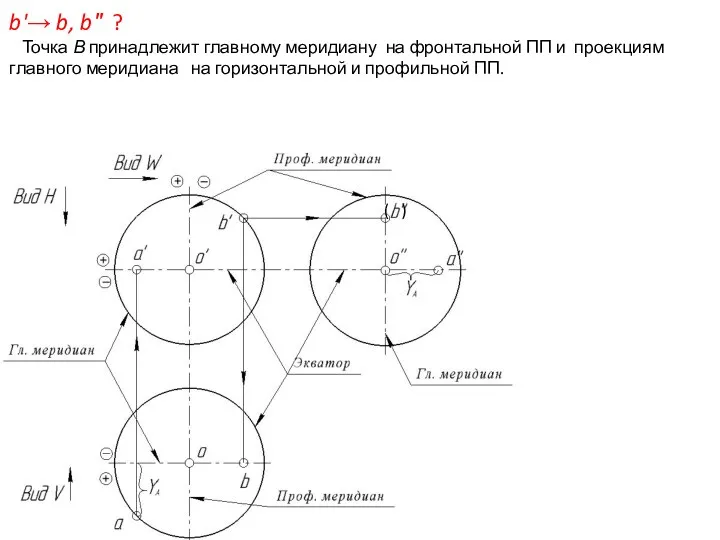
- 51. b'→ b, b″ ? Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного меридиана
- 52. b'→ b, b″ ? Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного меридиана
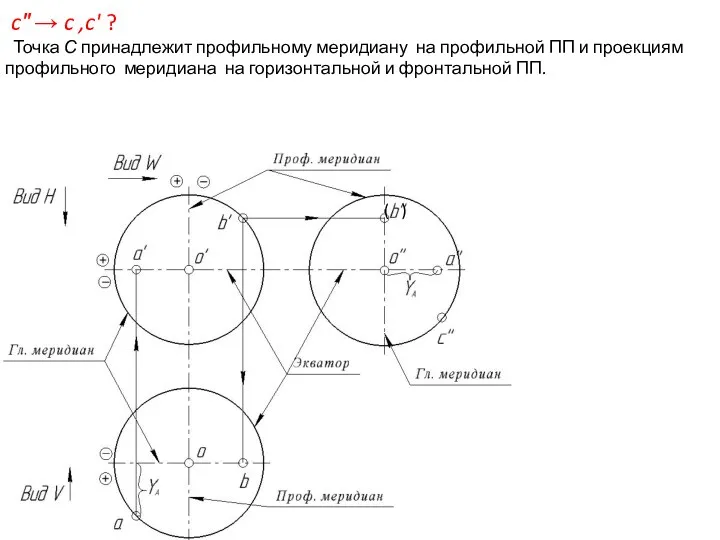
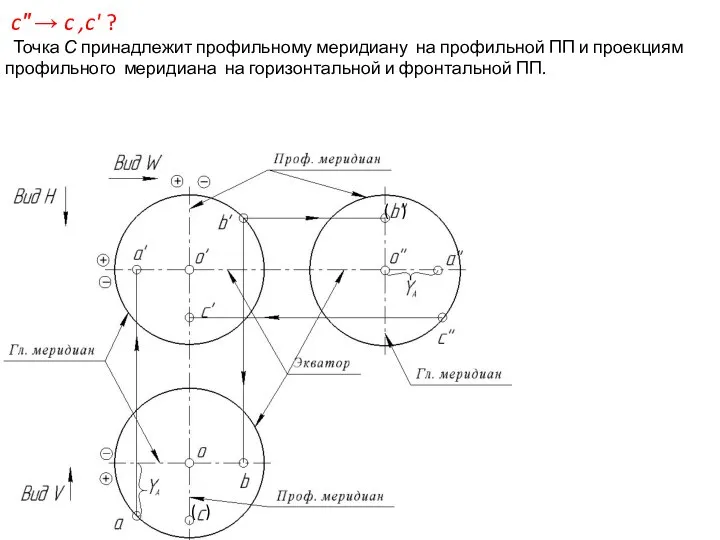
- 53. c″ → c ,c' ? Точка С принадлежит профильному меридиану на профильной ПП и проекциям профильного
- 54. c″ → c ,c' ? Точка С принадлежит профильному меридиану на профильной ПП и проекциям профильного
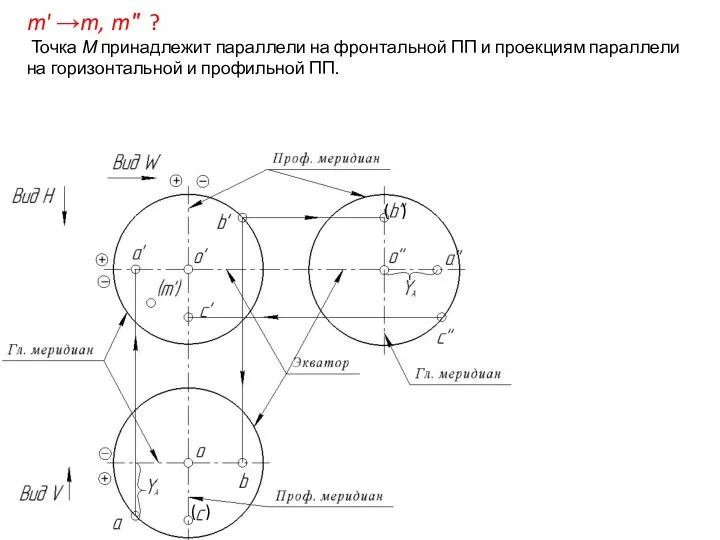
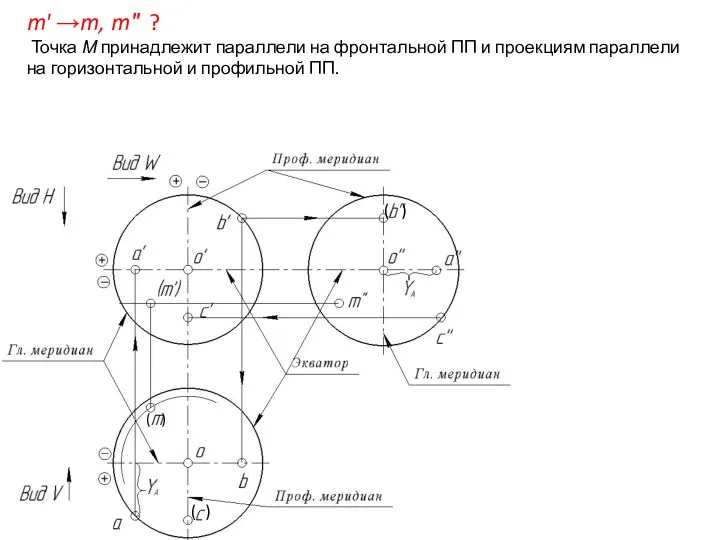
- 55. m' →m, m″ ? Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на горизонтальной
- 56. m' →m, m″ ? Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на горизонтальной
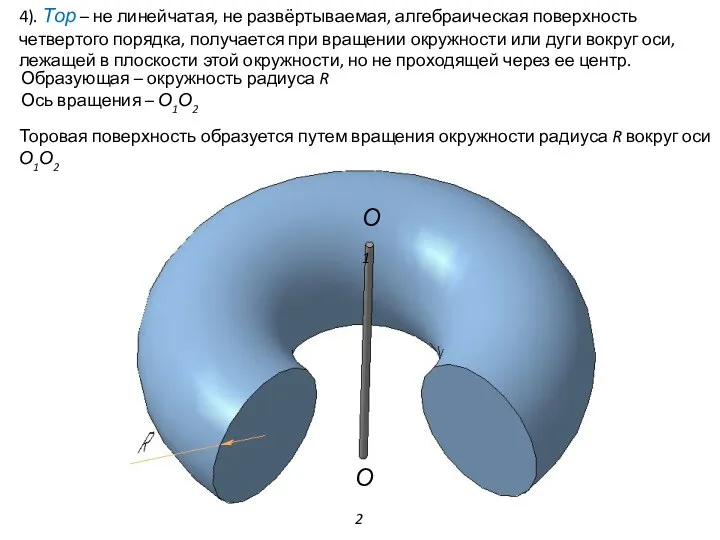
- 57. 4). Тор – не линейчатая, не развёртываемая, алгебраическая поверхность четвертого порядка, получается при вращении окружности или
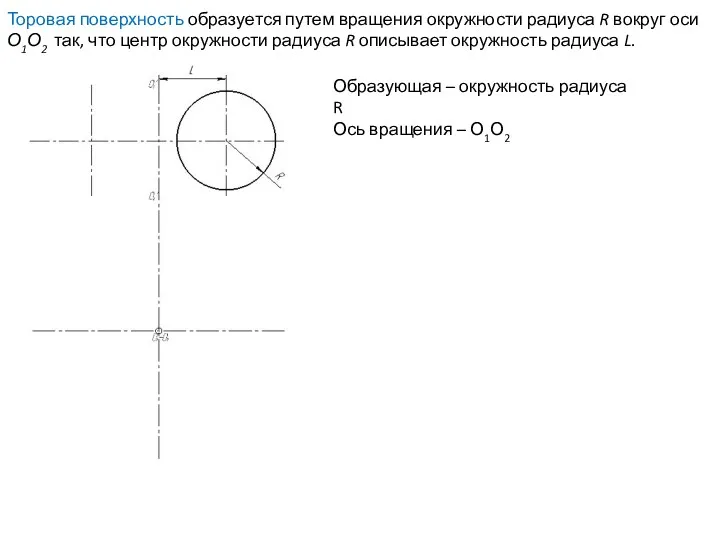
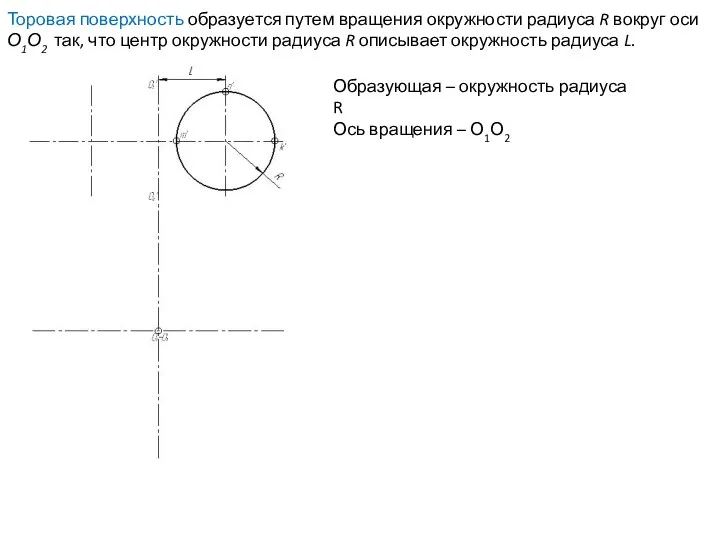
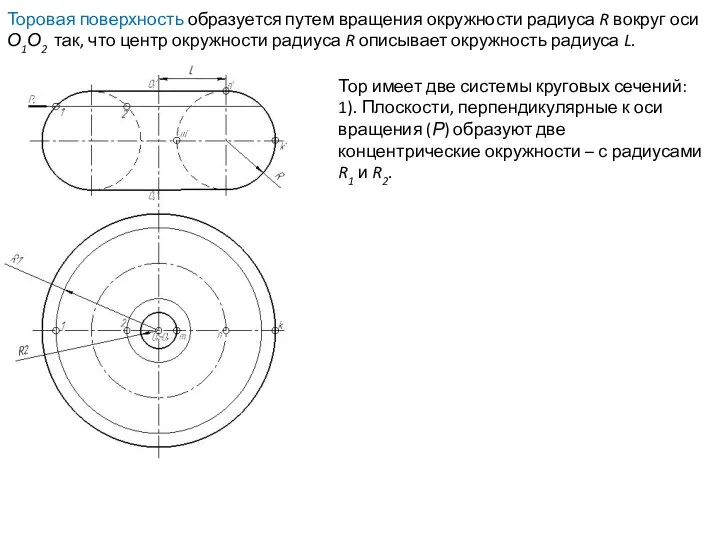
- 58. Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2 так, что центр окружности радиуса
- 59. Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2 так, что центр окружности радиуса
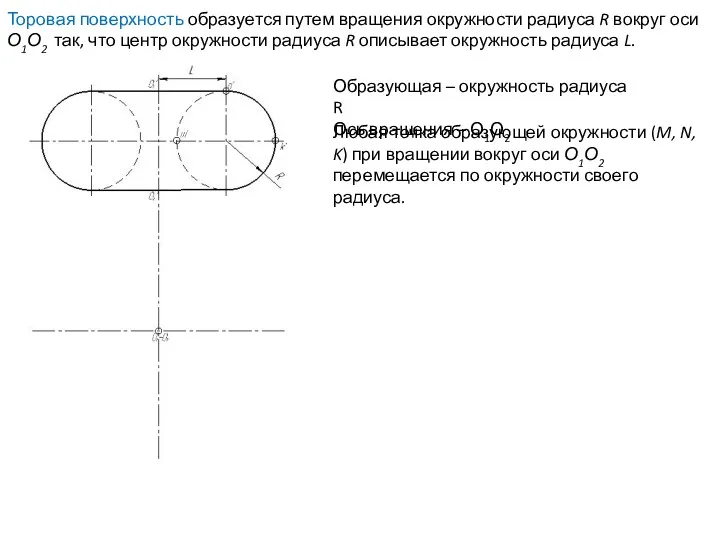
- 60. Любая точка образующей окружности (M, N, K) при вращении вокруг оси О1О2 перемещается по окружности своего
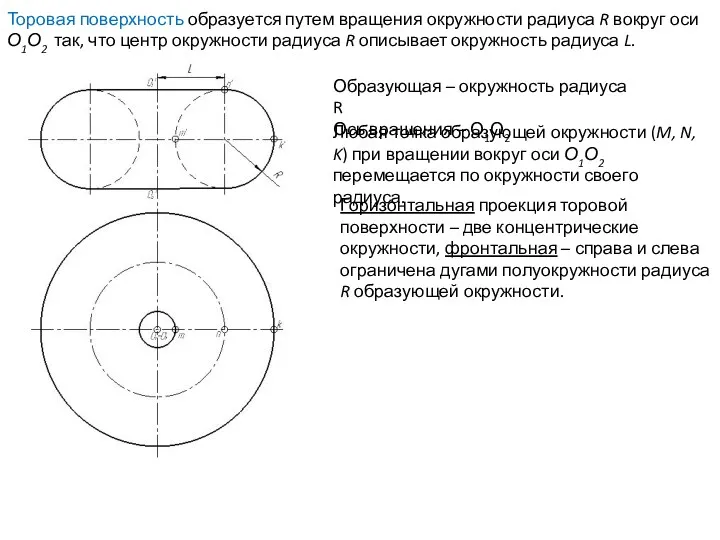
- 61. Горизонтальная проекция торовой поверхности – две концентрические окружности, фронтальная – справа и слева ограничена дугами полуокружности
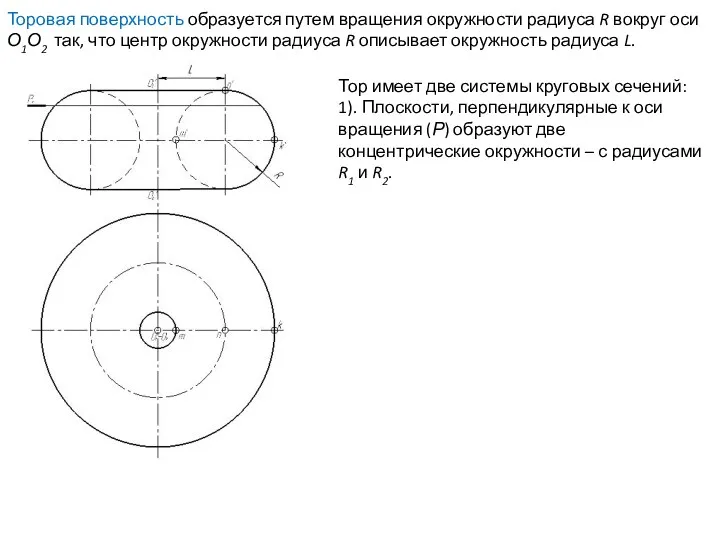
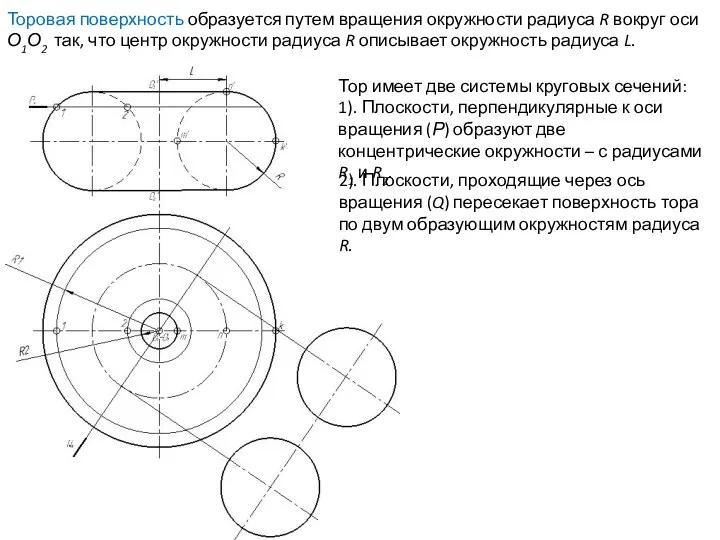
- 62. Тор имеет две системы круговых сечений: 1). Плоскости, перпендикулярные к оси вращения (Р) образуют две концентрические
- 63. Тор имеет две системы круговых сечений: 1). Плоскости, перпендикулярные к оси вращения (Р) образуют две концентрические
- 64. 2). Плоскости, проходящие через ось вращения (Q) пересекает поверхность тора по двум образующим окружностям радиуса R.
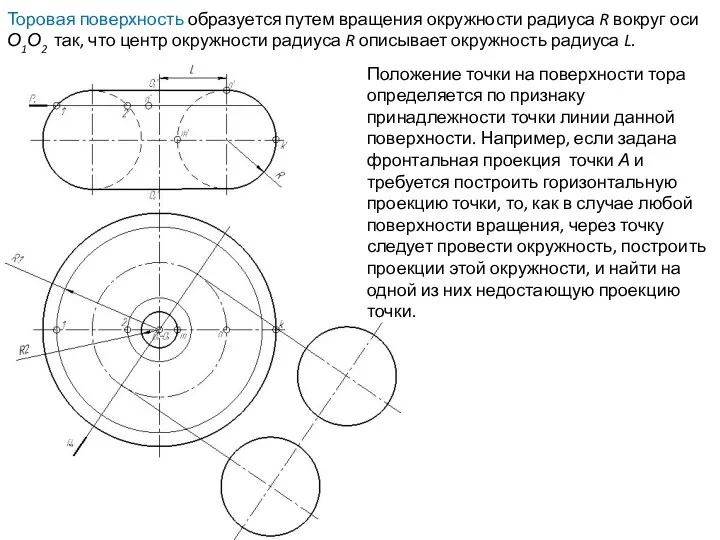
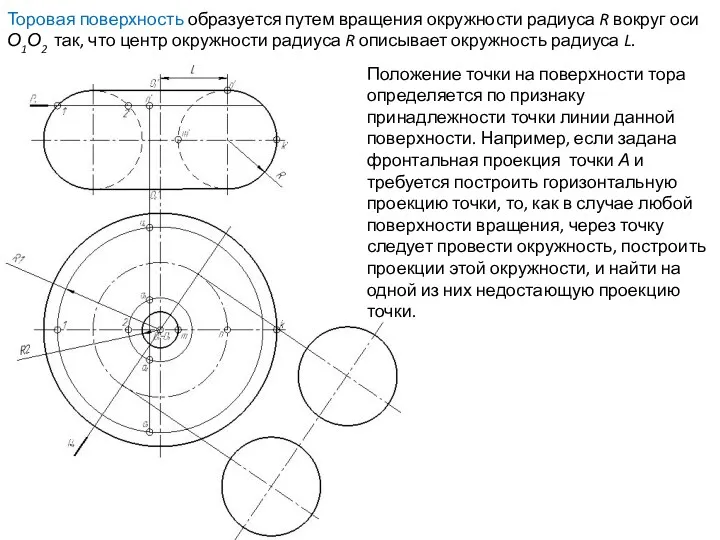
- 65. Положение точки на поверхности тора определяется по признаку принадлежности точки линии данной поверхности. Например, если задана
- 66. Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2 так, что центр окружности радиуса
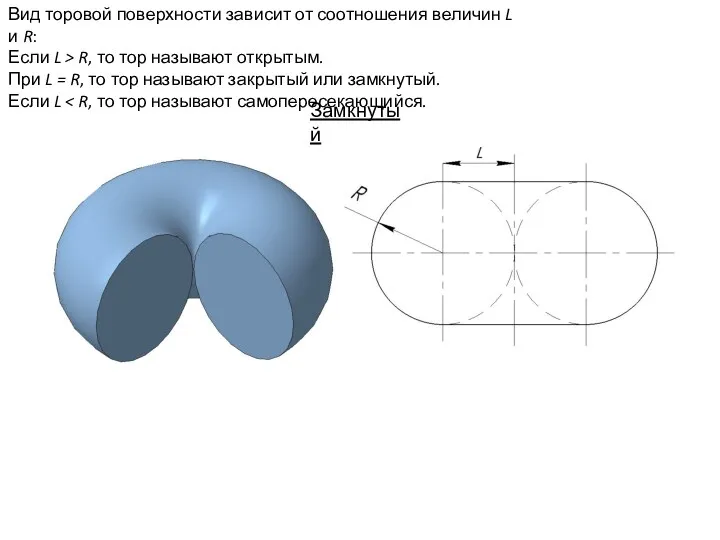
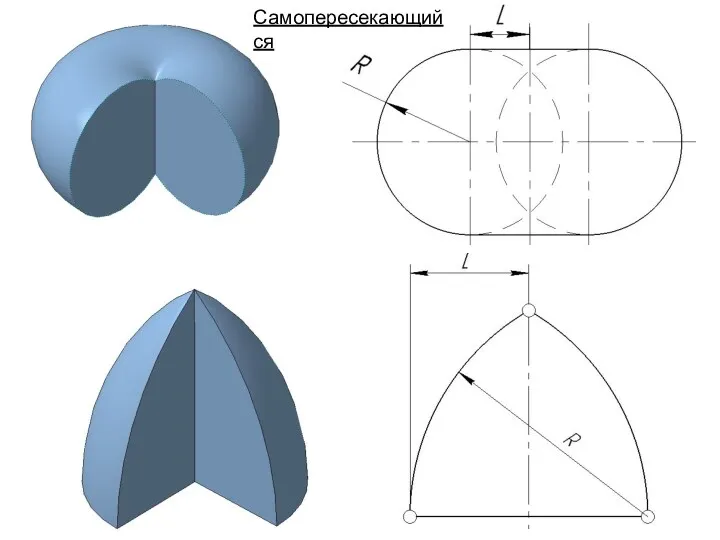
- 67. Вид торовой поверхности зависит от соотношения величин L и R: Если L > R, то тор
- 68. Самопересекающийся
- 69. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
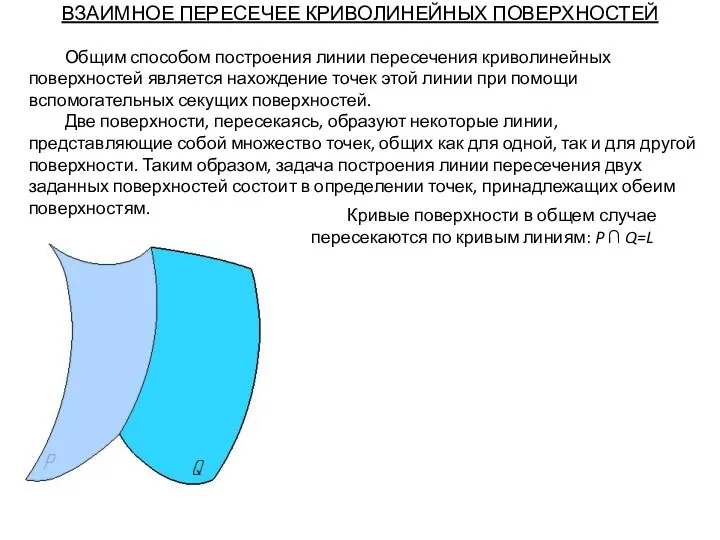
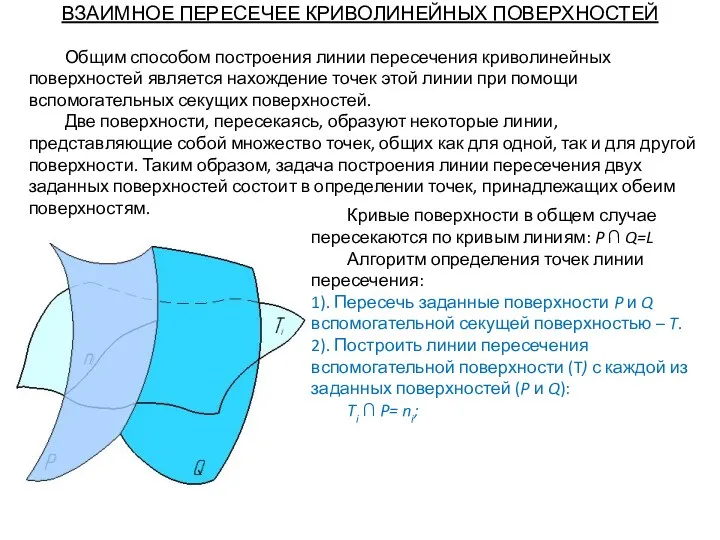
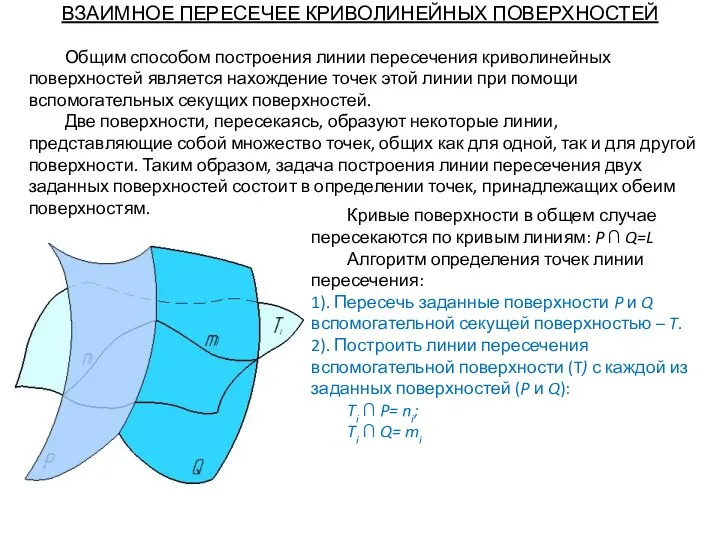
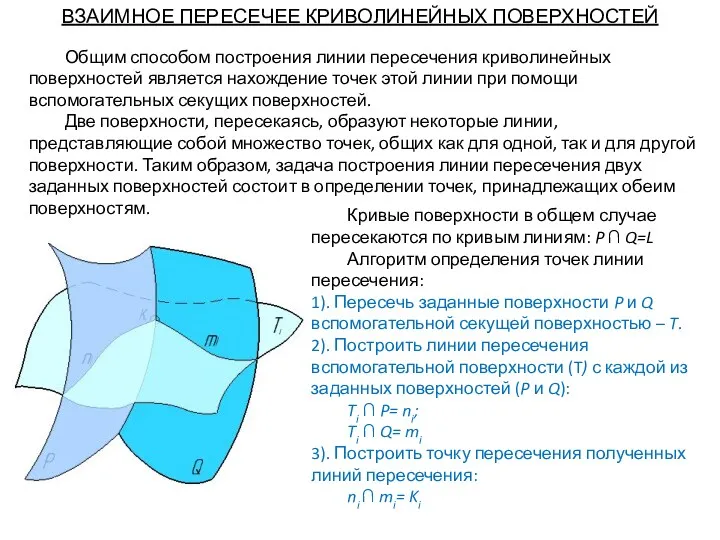
- 70. ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ Общим способом построения линии пересечения криволинейных поверхностей является нахождение точек этой линии
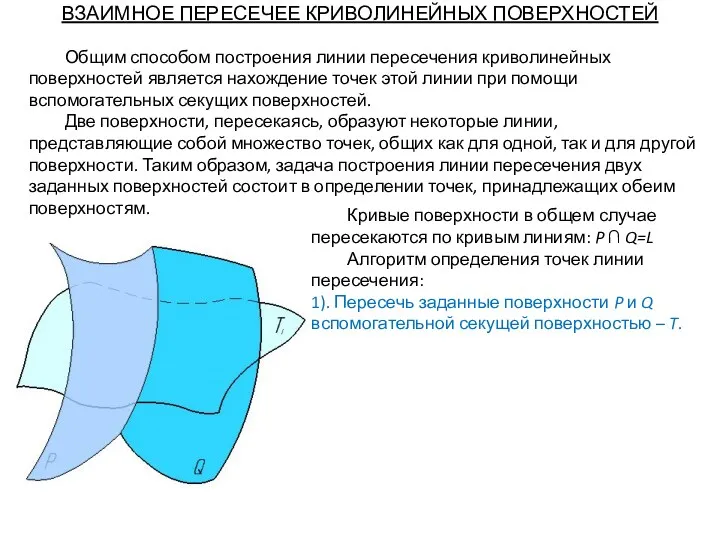
- 71. Общим способом построения линии пересечения криволинейных поверхностей является нахождение точек этой линии при помощи вспомогательных секущих
- 72. Общим способом построения линии пересечения криволинейных поверхностей является нахождение точек этой линии при помощи вспомогательных секущих
- 73. Общим способом построения линии пересечения криволинейных поверхностей является нахождение точек этой линии при помощи вспомогательных секущих
- 74. Общим способом построения линии пересечения криволинейных поверхностей является нахождение точек этой линии при помощи вспомогательных секущих
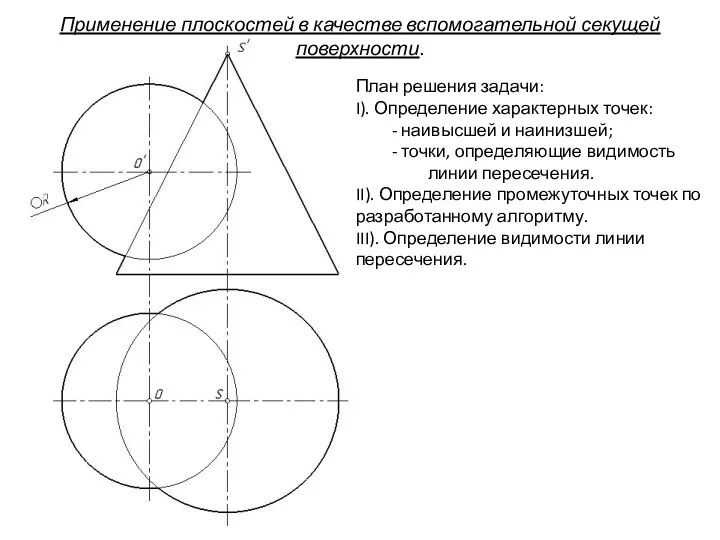
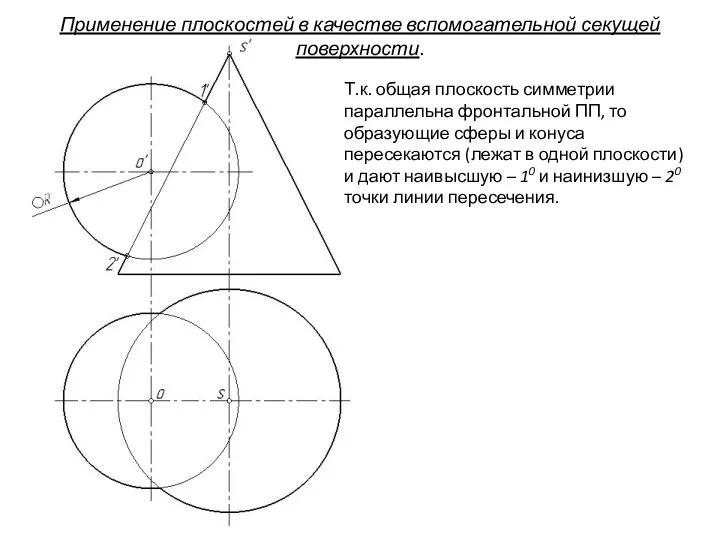
- 75. Применение плоскостей в качестве вспомогательной секущей поверхности. План решения задачи: I). Определение характерных точек: - наивысшей
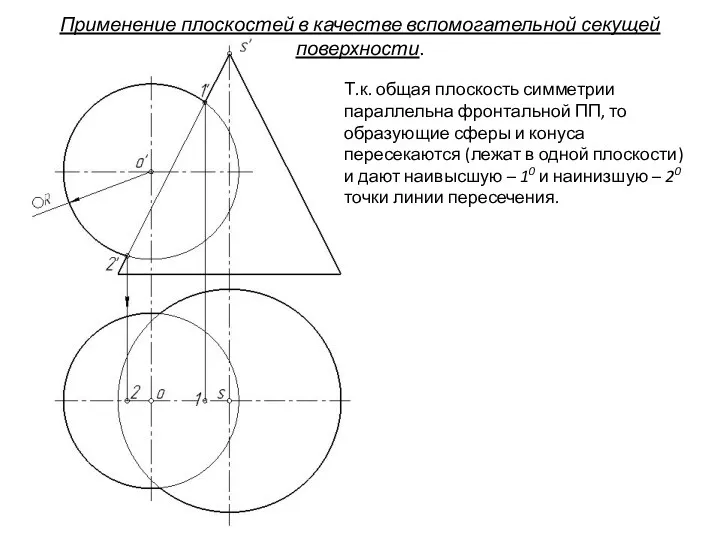
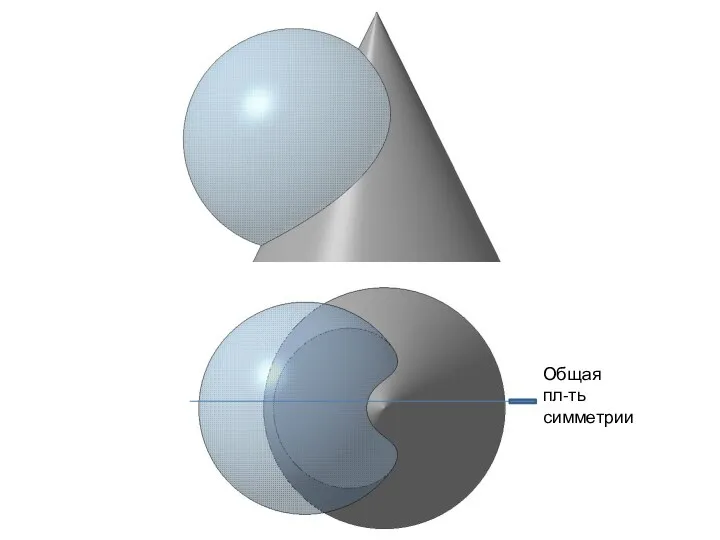
- 76. Т.к. общая плоскость симметрии параллельна фронтальной ПП, то образующие сферы и конуса пересекаются (лежат в одной
- 77. Применение плоскостей в качестве вспомогательной секущей поверхности. Т.к. общая плоскость симметрии параллельна фронтальной ПП, то образующие
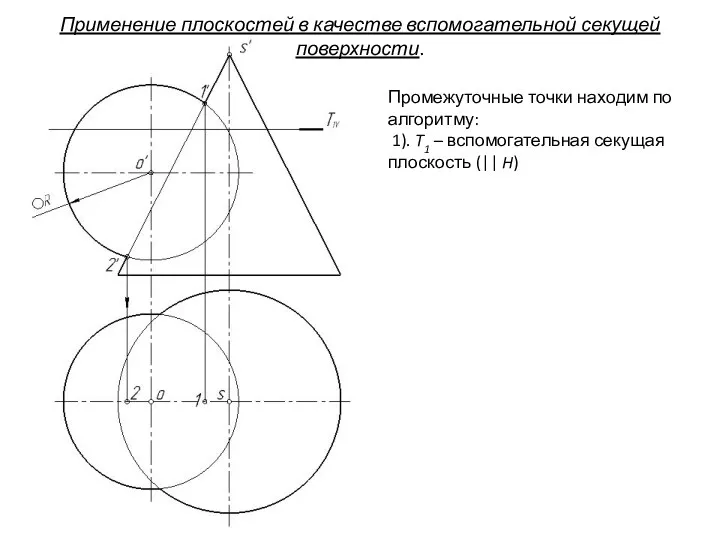
- 78. Промежуточные точки находим по алгоритму: 1). T1 – вспомогательная секущая плоскость (|| H) Применение плоскостей в
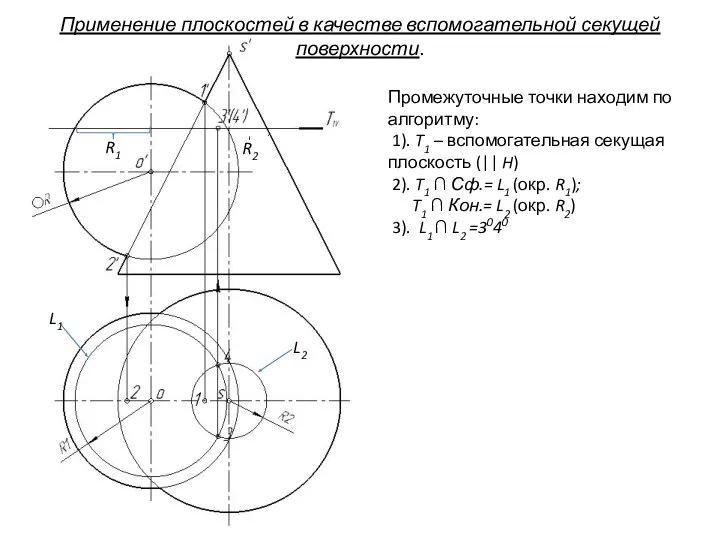
- 79. Промежуточные точки находим по алгоритму: 1). T1 – вспомогательная секущая плоскость (|| H) 2). T1 ∩
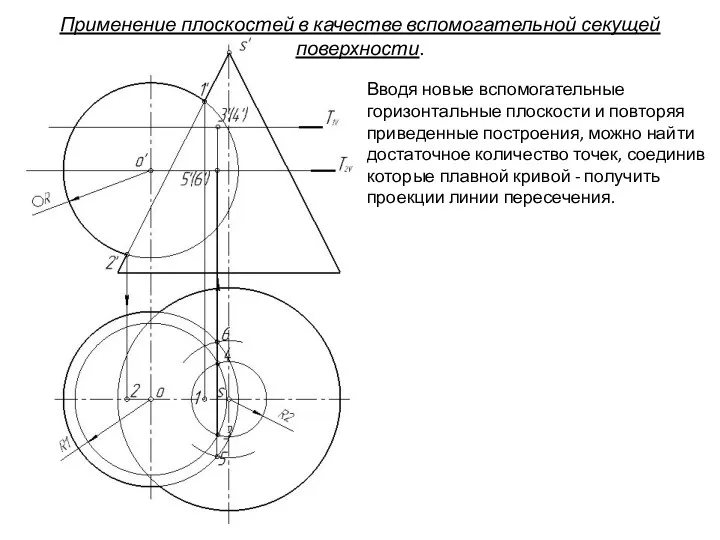
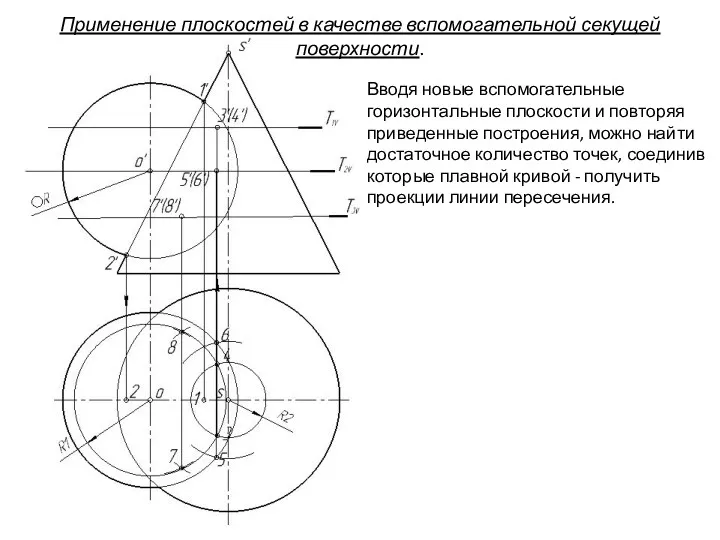
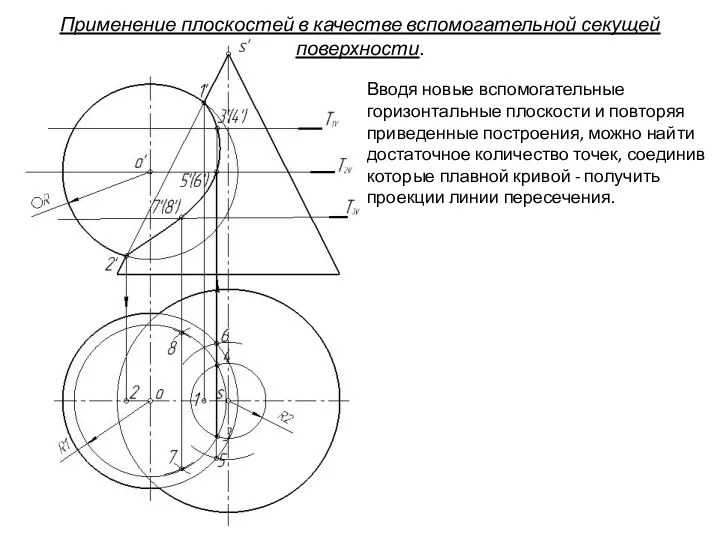
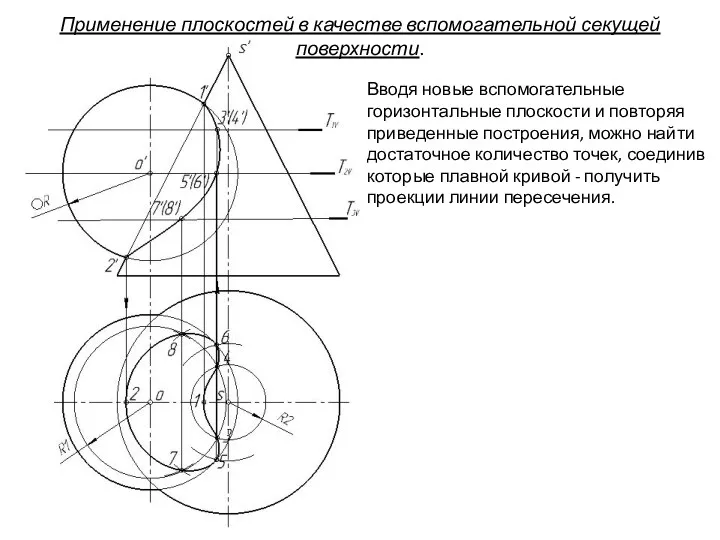
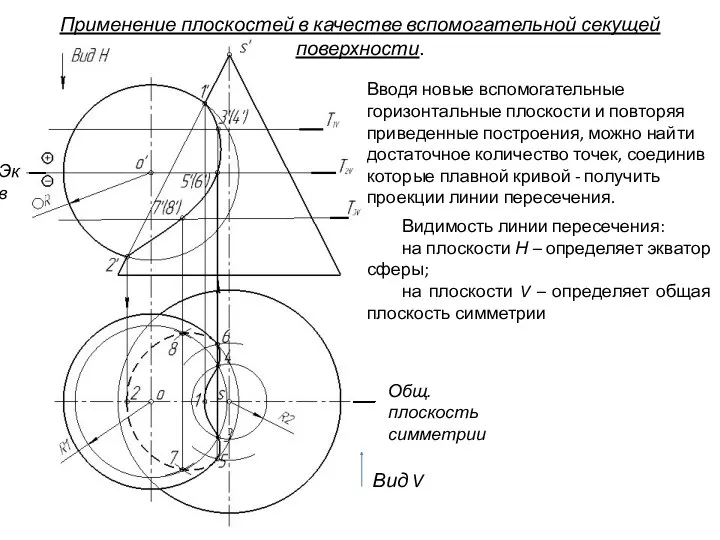
- 80. Вводя новые вспомогательные горизонтальные плоскости и повторяя приведенные построения, можно найти достаточное количество точек, соединив которые
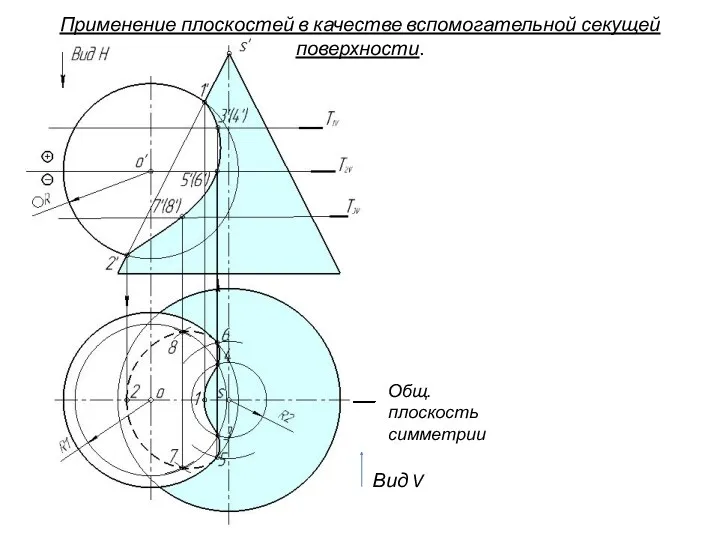
- 81. Применение плоскостей в качестве вспомогательной секущей поверхности. Вводя новые вспомогательные горизонтальные плоскости и повторяя приведенные построения,
- 82. Применение плоскостей в качестве вспомогательной секущей поверхности. Вводя новые вспомогательные горизонтальные плоскости и повторяя приведенные построения,
- 83. Применение плоскостей в качестве вспомогательной секущей поверхности. Вводя новые вспомогательные горизонтальные плоскости и повторяя приведенные построения,
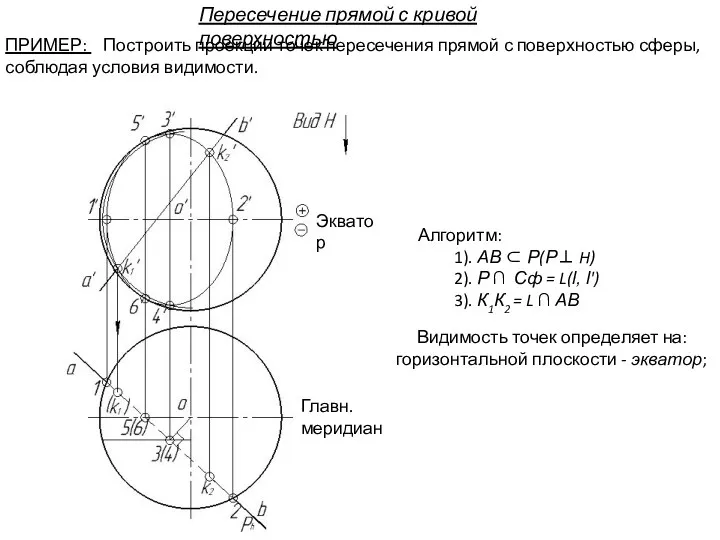
- 84. Применение плоскостей в качестве вспомогательной секущей поверхности. Видимость линии пересечения: на плоскости Н – определяет экватор
- 85. Применение плоскостей в качестве вспомогательной секущей поверхности. Вид V Общ. плоскость симметрии
- 86. Общая пл-ть симметрии
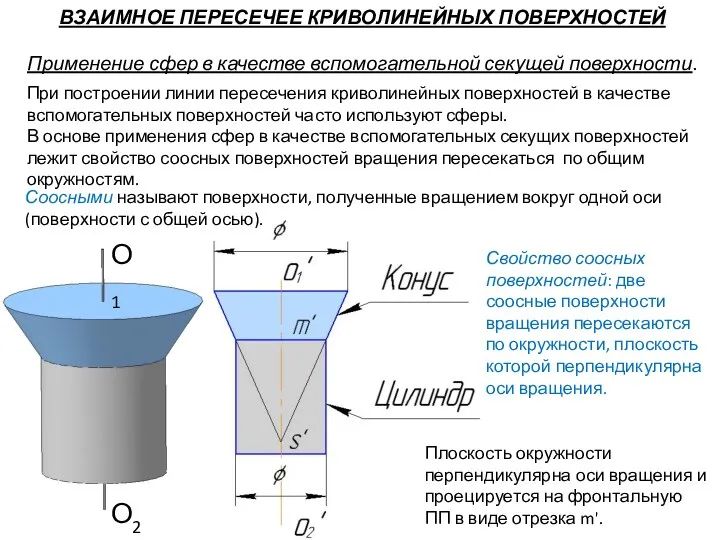
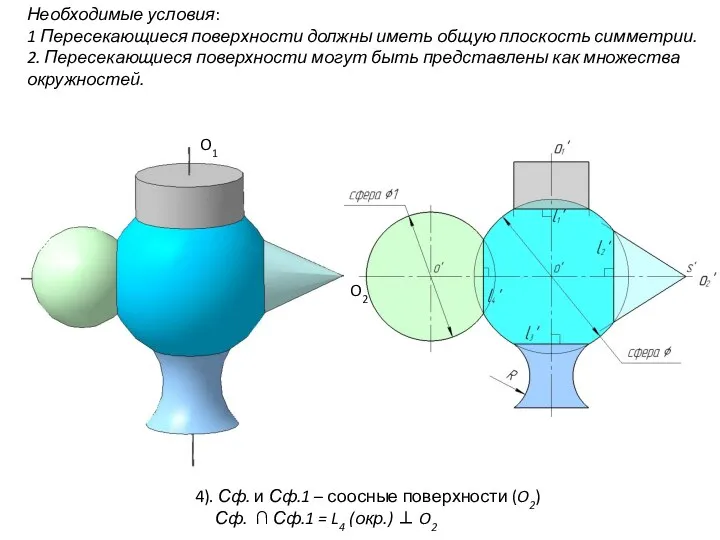
- 87. ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ Применение сфер в качестве вспомогательной секущей поверхности. При построении линии пересечения криволинейных
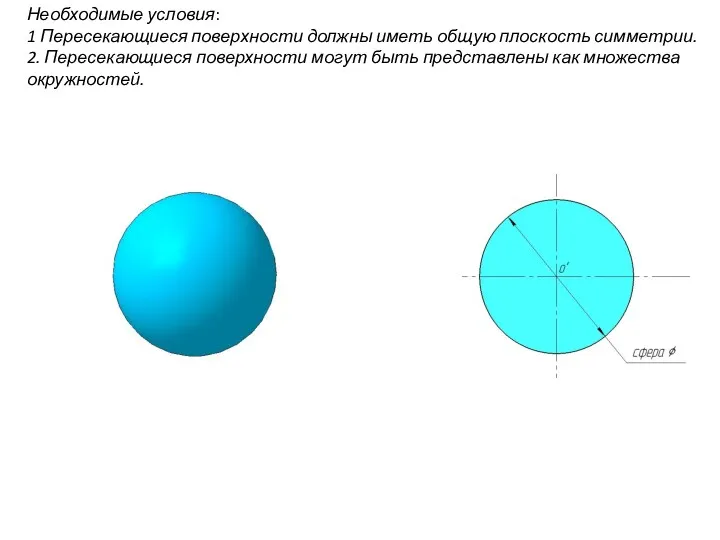
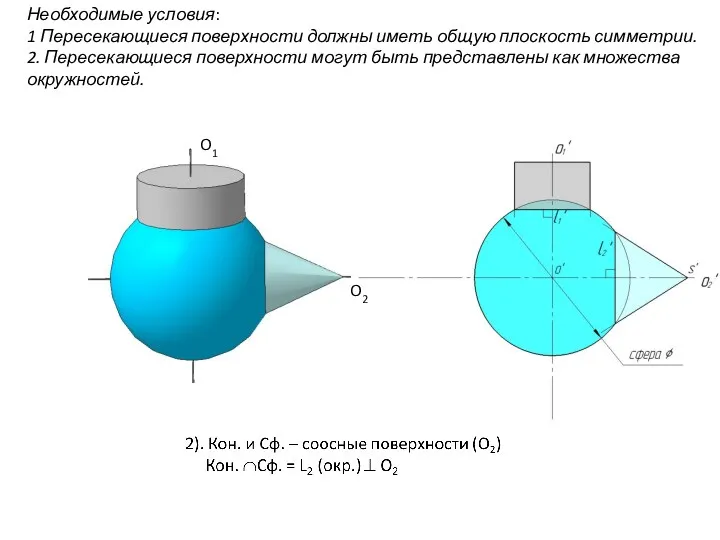
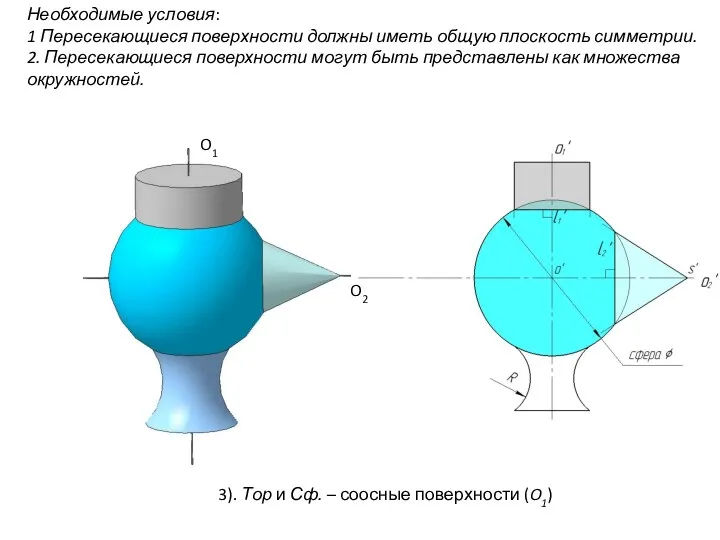
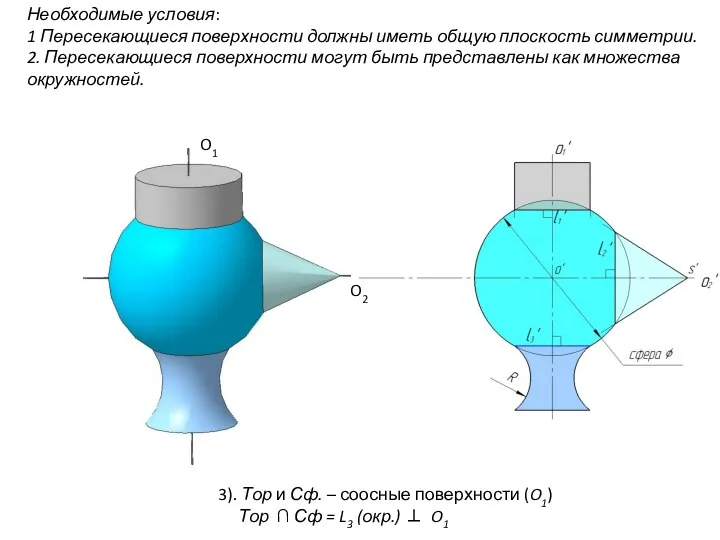
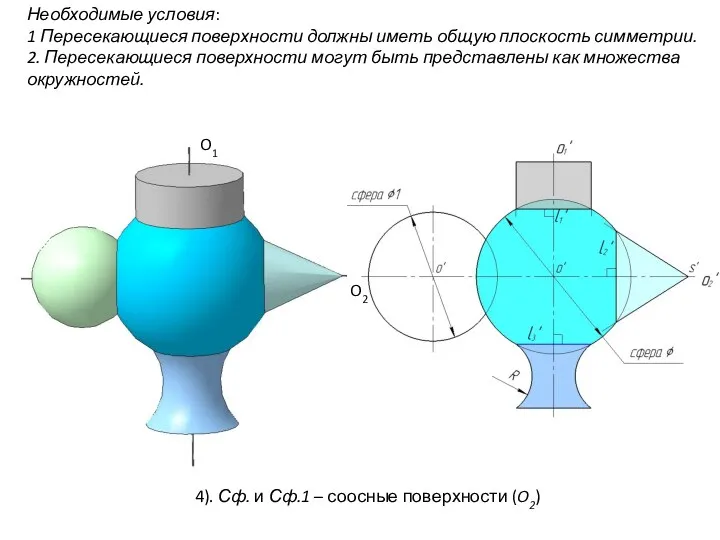
- 88. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
- 89. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
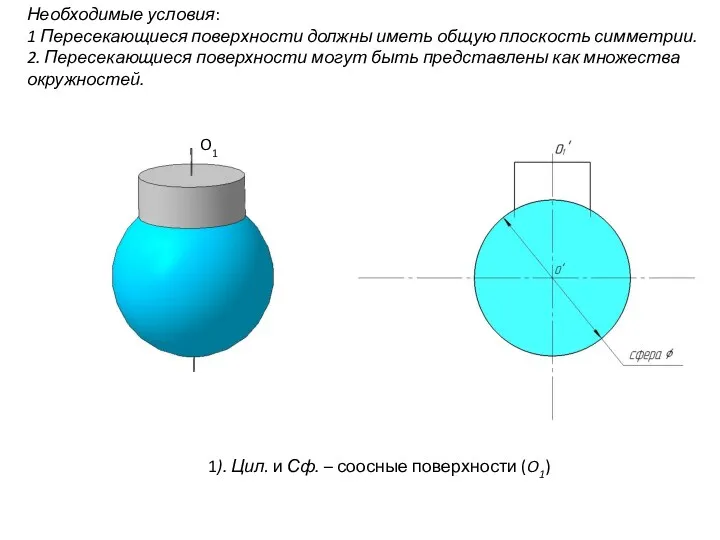
- 90. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
- 91. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
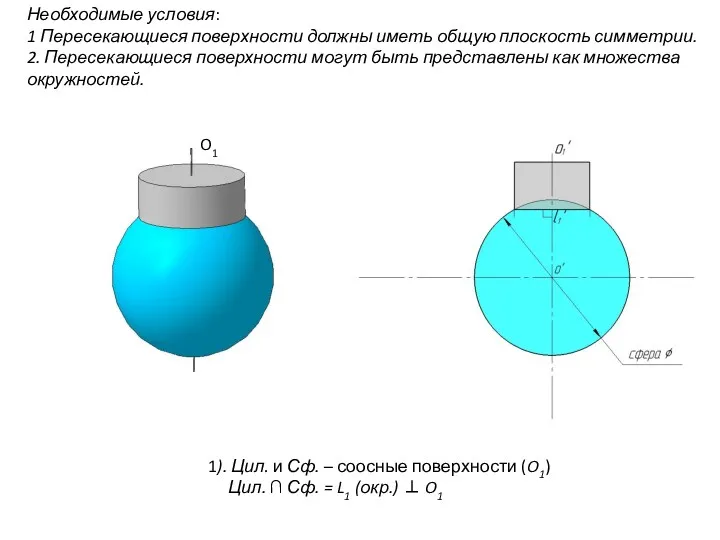
- 92. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
- 93. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
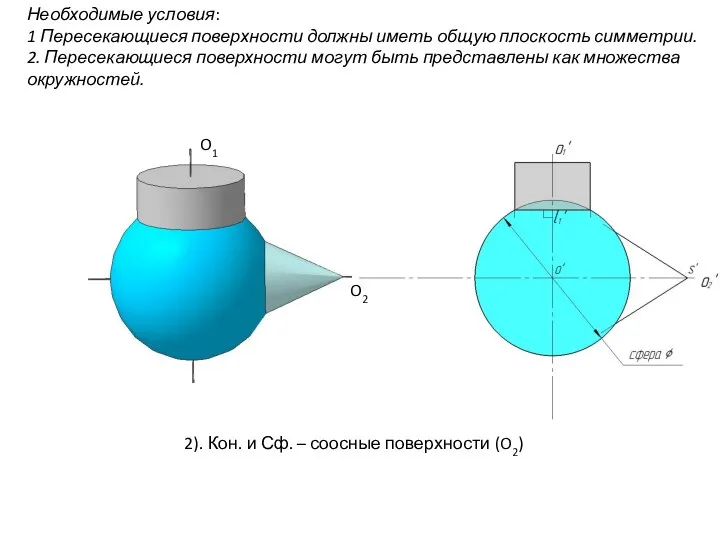
- 94. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
- 95. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
- 96. Необходимые условия: 1 Пересекающиеся поверхности должны иметь общую плоскость симметрии. 2. Пересекающиеся поверхности могут быть представлены
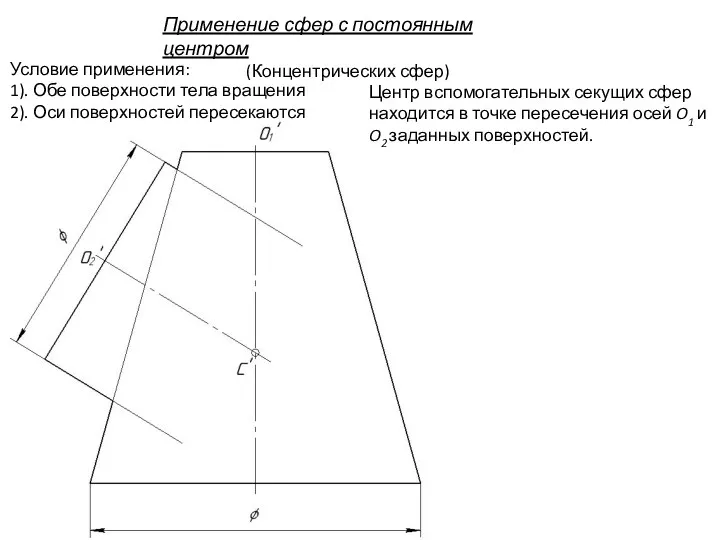
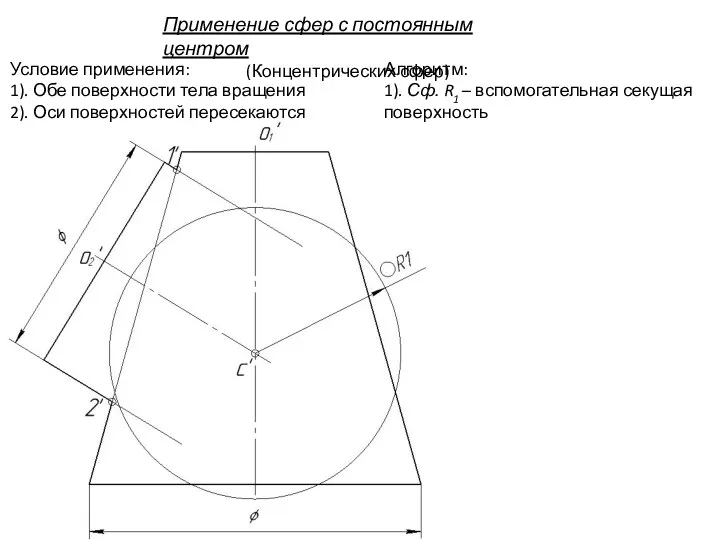
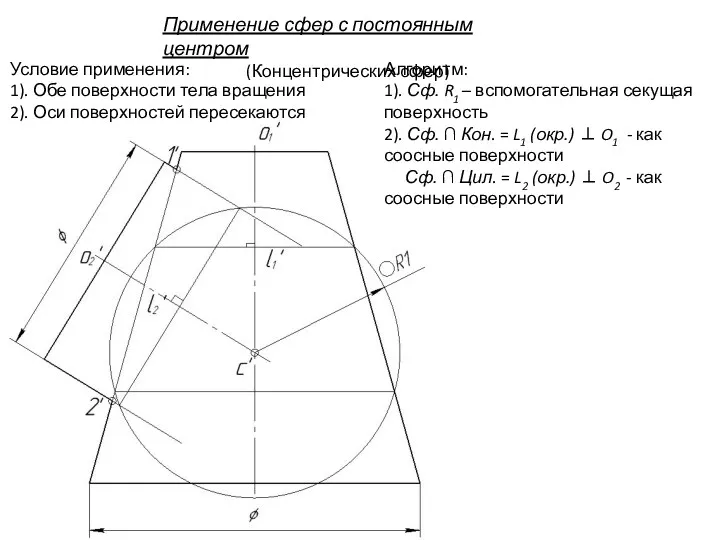
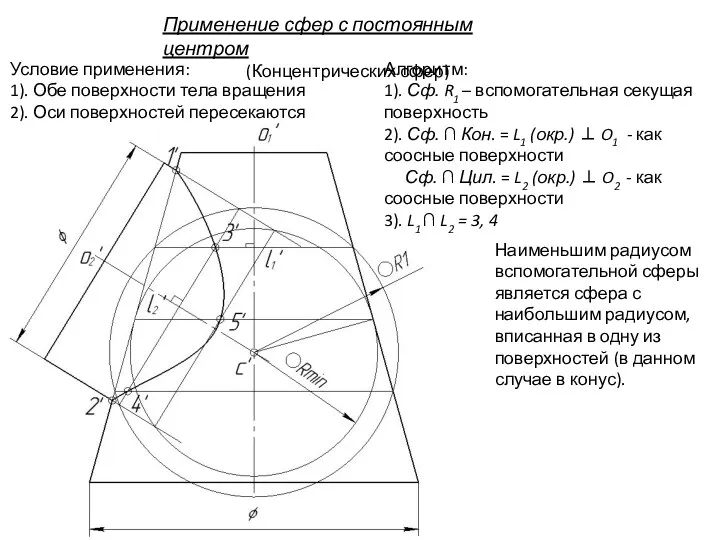
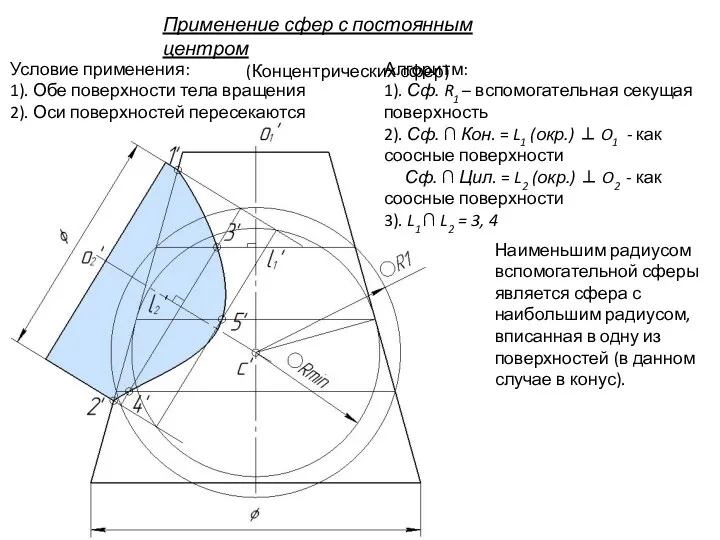
- 97. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
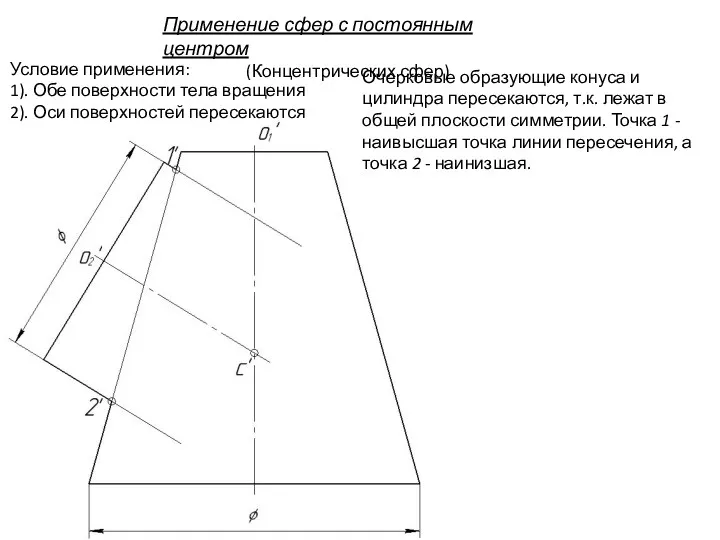
- 98. Очерковые образующие конуса и цилиндра пересекаются, т.к. лежат в общей плоскости симметрии. Точка 1 - наивысшая
- 99. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
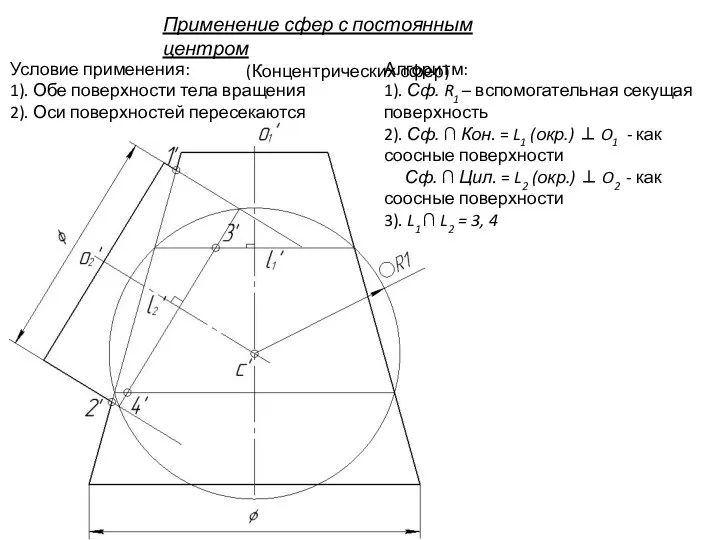
- 100. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
- 101. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
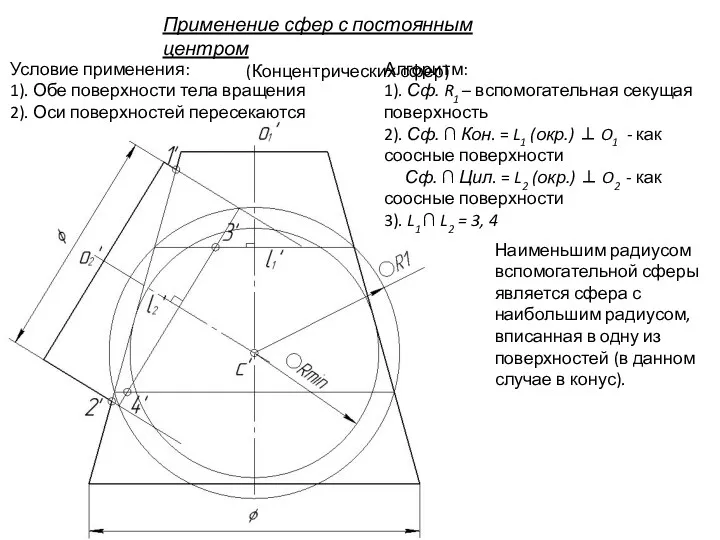
- 102. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
- 103. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
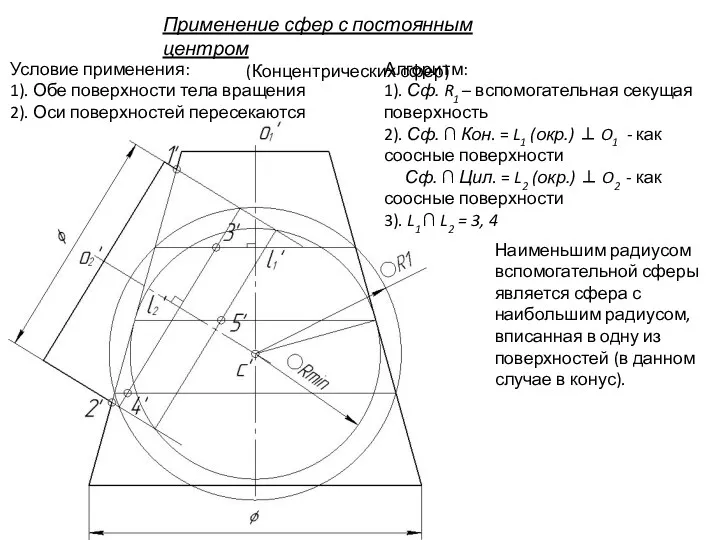
- 104. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
- 105. Применение сфер с постоянным центром (Концентрических сфер) Условие применения: 1). Обе поверхности тела вращения 2). Оси
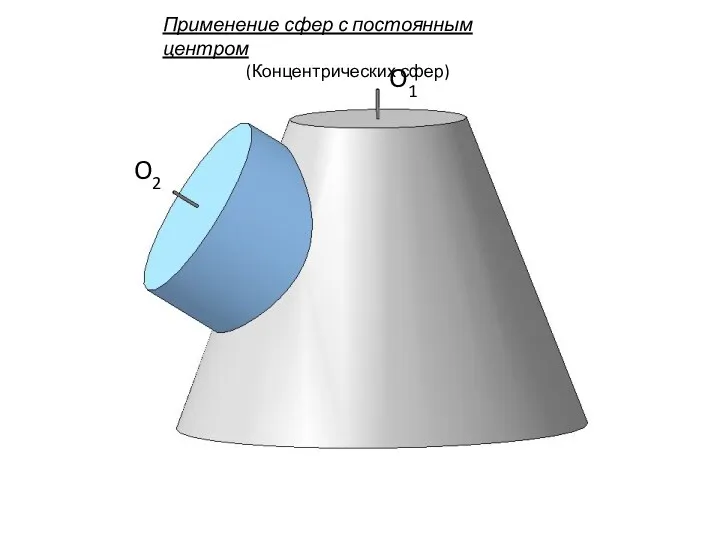
- 106. O1 O2 Применение сфер с постоянным центром (Концентрических сфер)
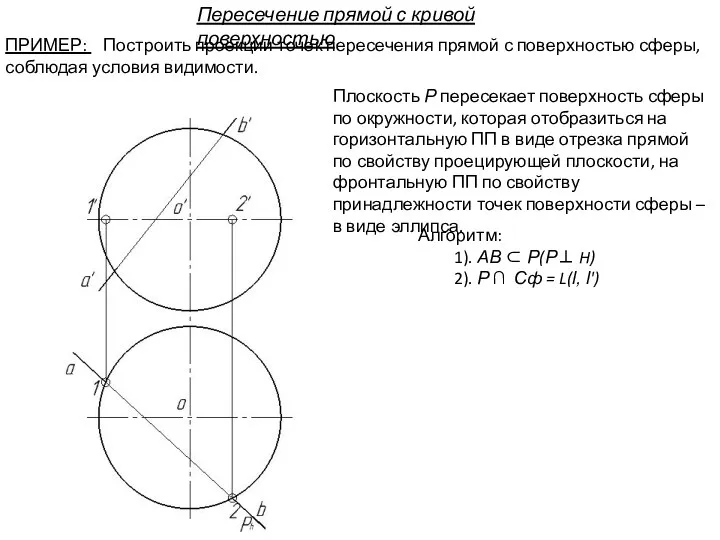
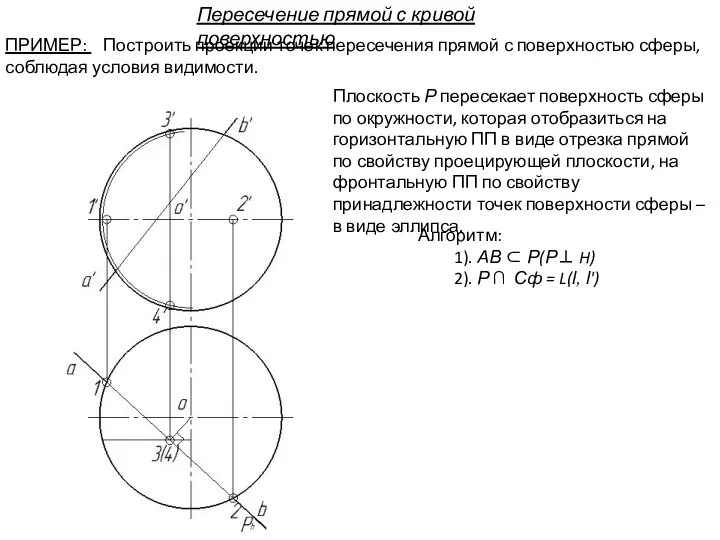
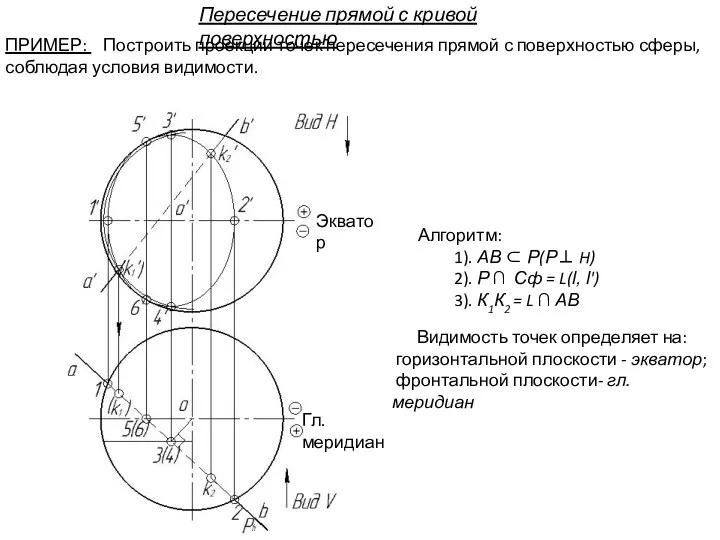
- 107. Пересечение прямой с кривой поверхностью ПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы, соблюдая условия
- 108. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') Плоскость Р пересекает
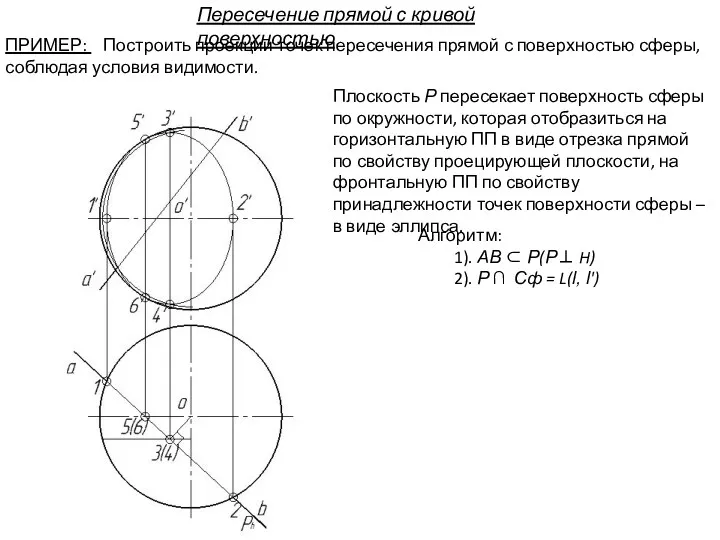
- 109. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') Плоскость Р пересекает
- 110. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') Плоскость Р пересекает
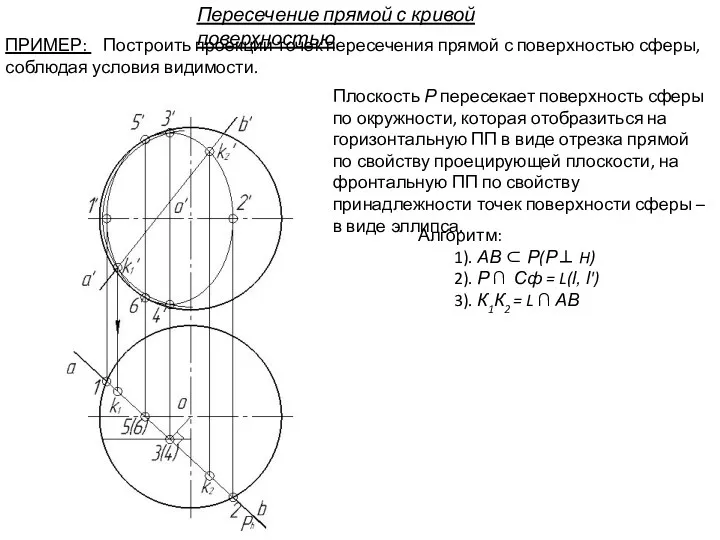
- 111. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') 3). К1К2 =
- 112. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') 3). К1К2 =
- 113. Алгоритм: 1). АВ ⊂ Р(Р⊥ H) 2). Р ∩ Сф = L(l, l') 3). К1К2 =
- 114. МНОГОГРАННИКИ
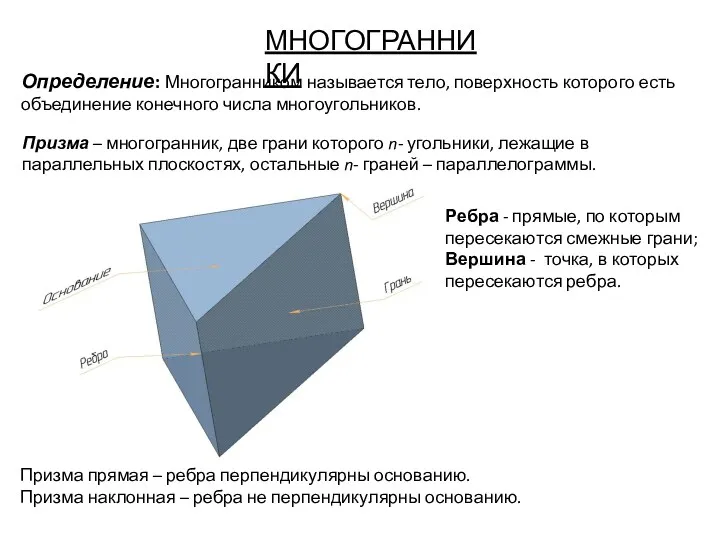
- 115. МНОГОГРАННИКИ Определение: Многогранником называется тело, поверхность которого есть объединение конечного числа многоугольников. Призма – многогранник, две
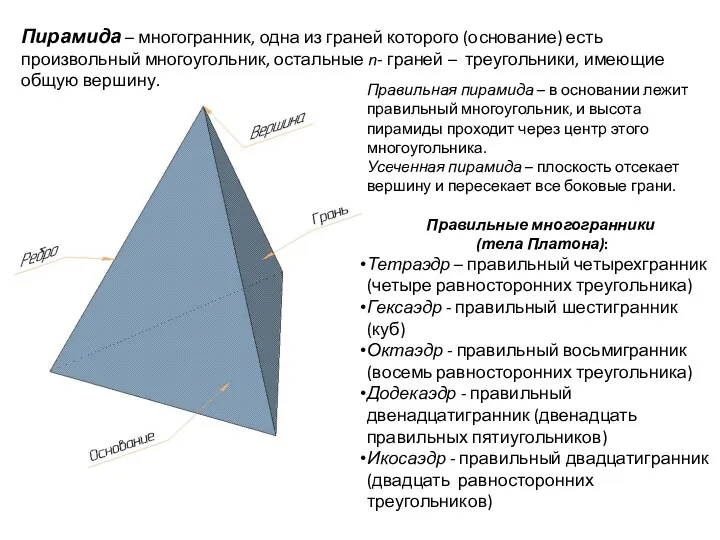
- 116. Пирамида – многогранник, одна из граней которого (основание) есть произвольный многоугольник, остальные n- граней – треугольники,
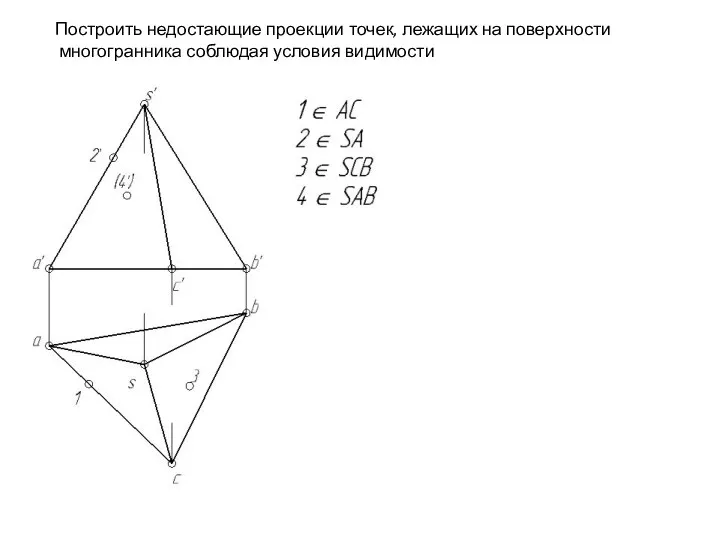
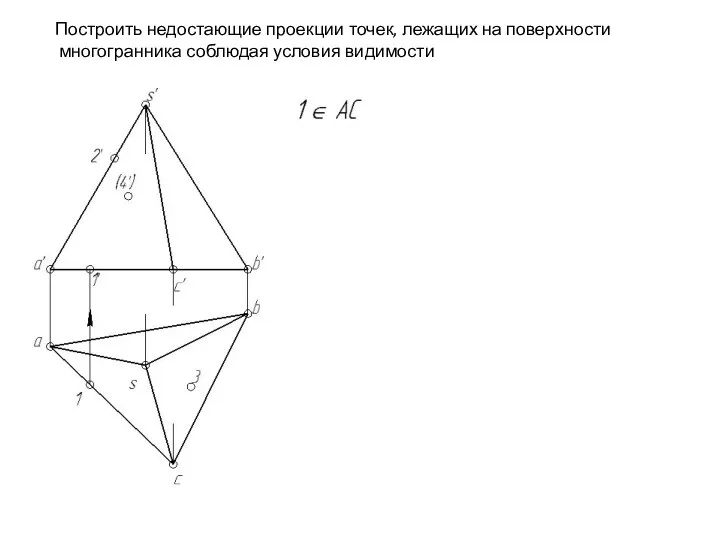
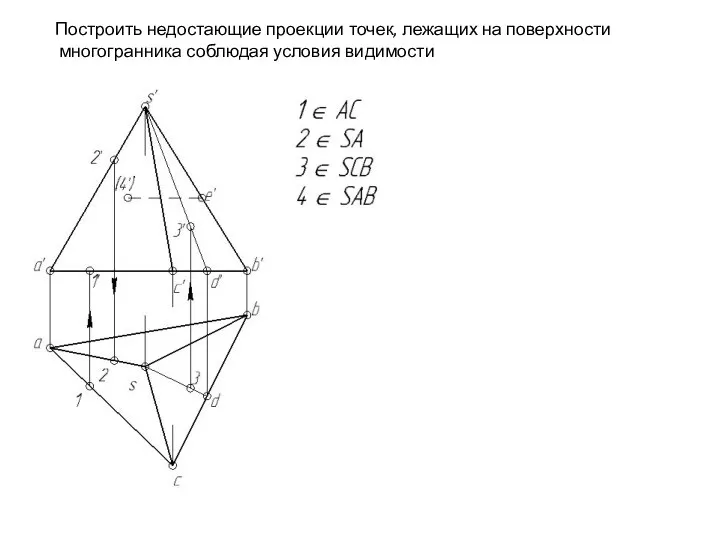
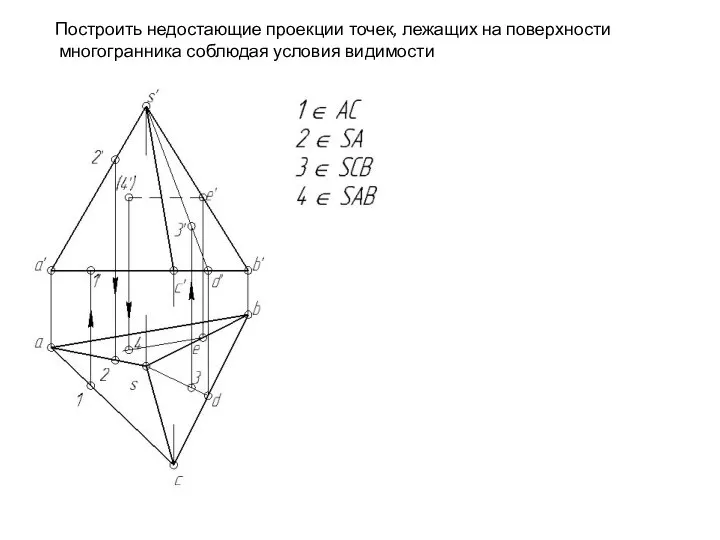
- 117. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
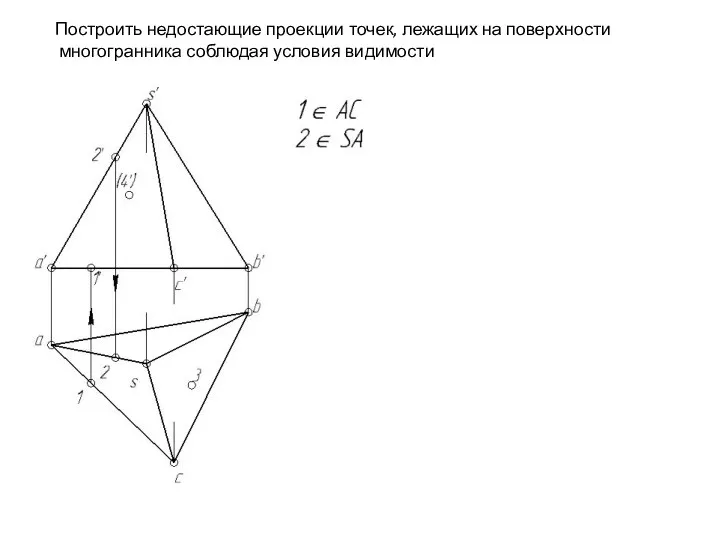
- 118. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
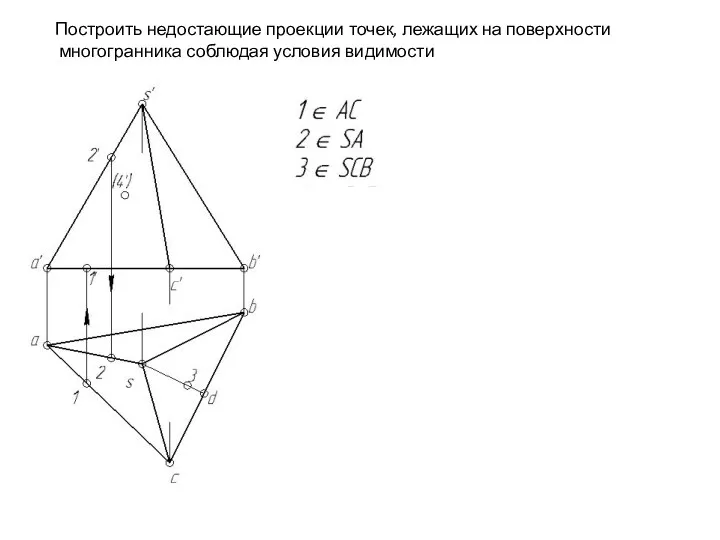
- 119. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
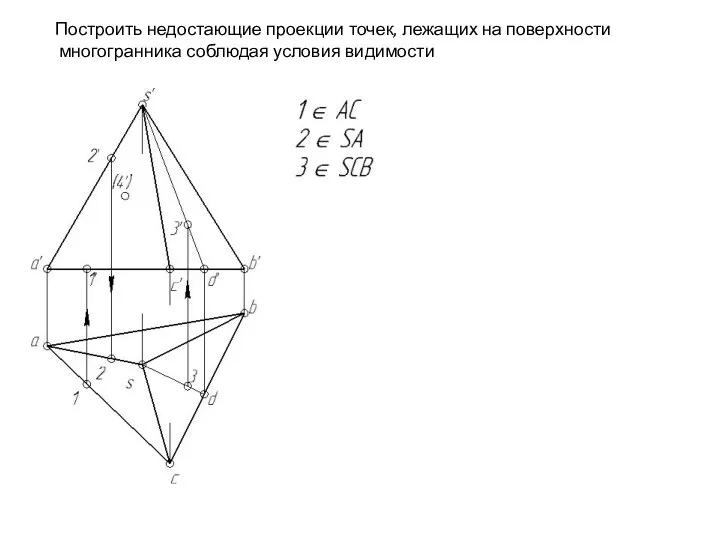
- 120. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 121. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 122. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
- 123. Построить недостающие проекции точек, лежащих на поверхности многогранника соблюдая условия видимости
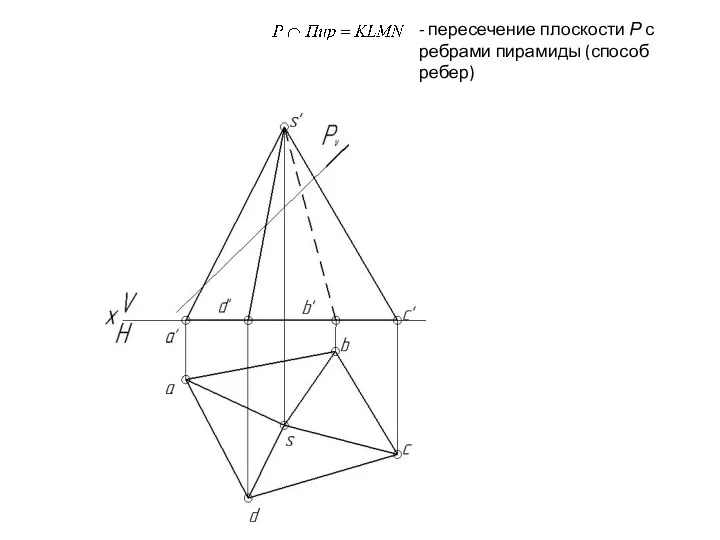
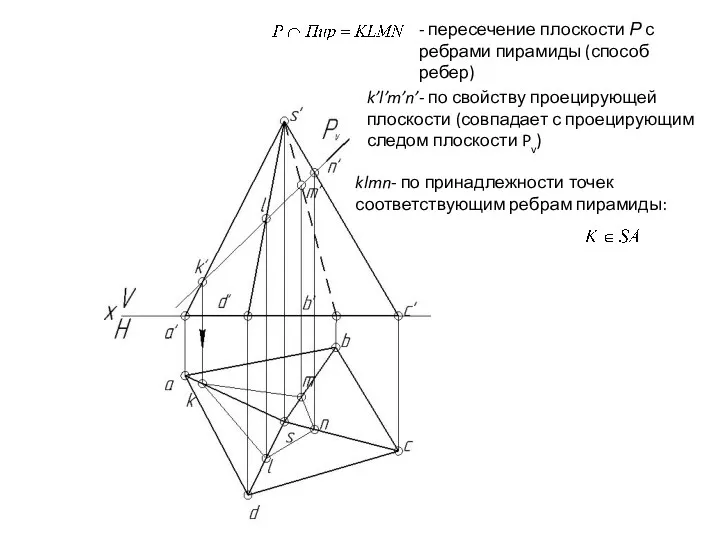
- 124. Пересечение многогранника проецирующей плоскостью. Натуральный вид фигуры сечения. Сечение многогранника – геометрическая фигура в результате пересечения
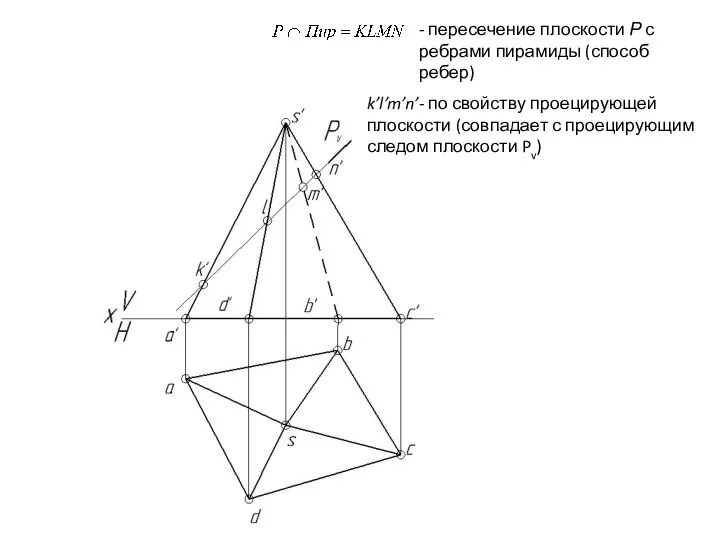
- 125. - пересечение плоскости Р с ребрами пирамиды (способ ребер)
- 126. - пересечение плоскости Р с ребрами пирамиды (способ ребер) k’l’m’n’- по свойству проецирующей плоскости (совпадает с
- 127. - пересечение плоскости Р с ребрами пирамиды (способ ребер) k’l’m’n’- по свойству проецирующей плоскости (совпадает с
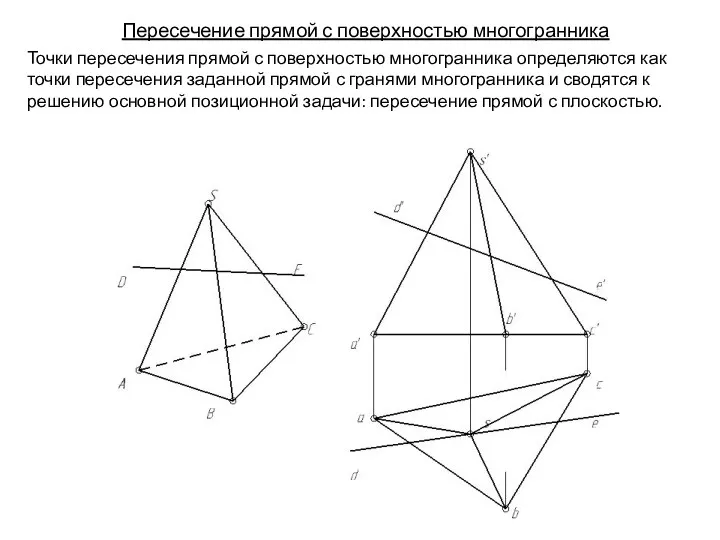
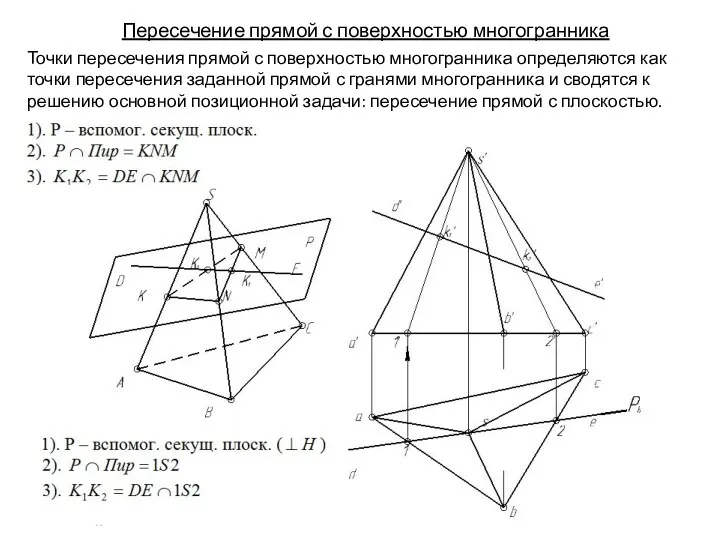
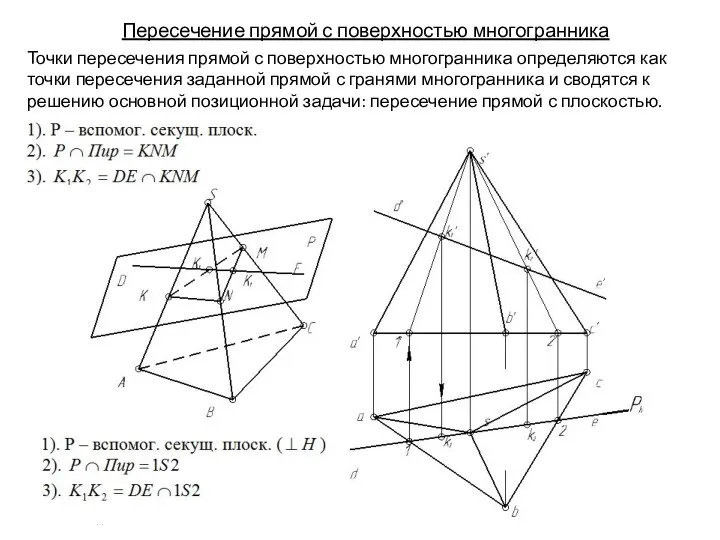
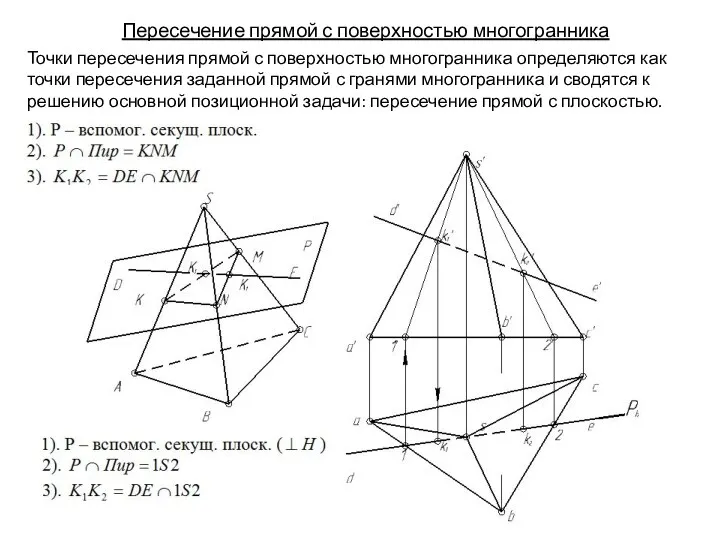
- 131. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
- 132. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
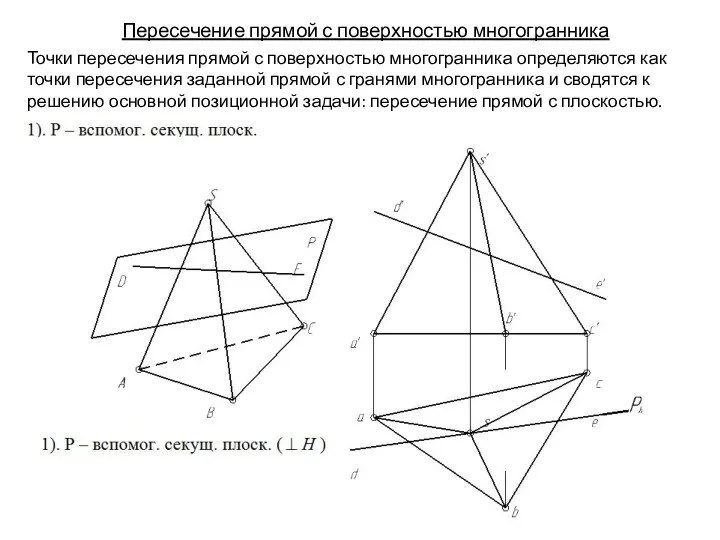
- 133. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
- 134. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
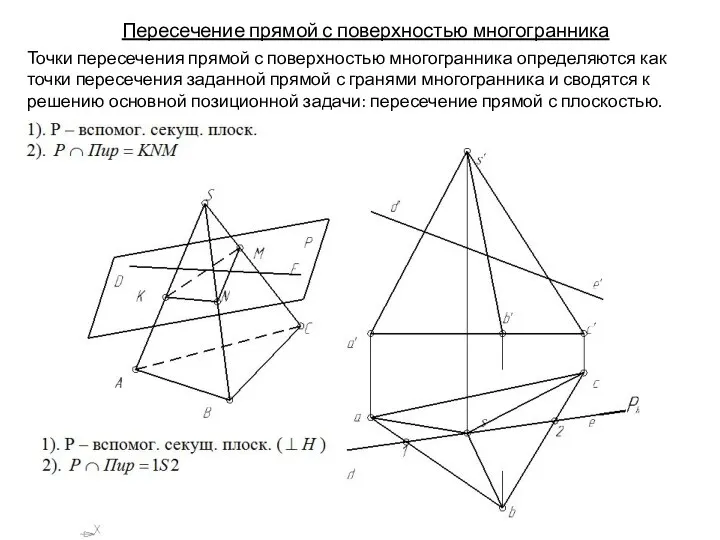
- 135. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
- 136. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
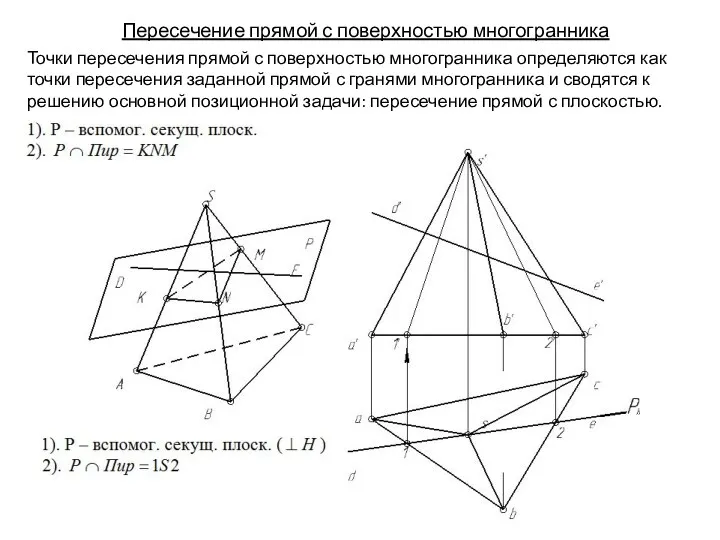
- 137. Пересечение прямой с поверхностью многогранника Точки пересечения прямой с поверхностью многогранника определяются как точки пересечения заданной
- 138. Взаимное пересечение многогранников Линию взаимного пересечения двух многогранников можно построить двумя способами: 1). Способ ребер –
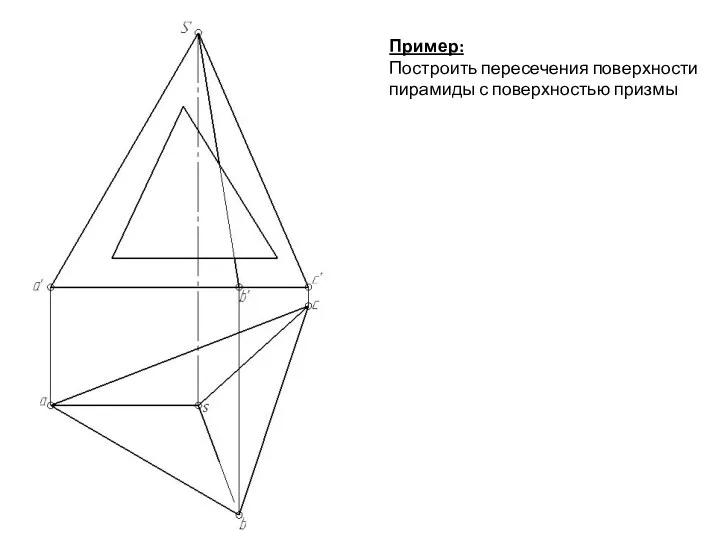
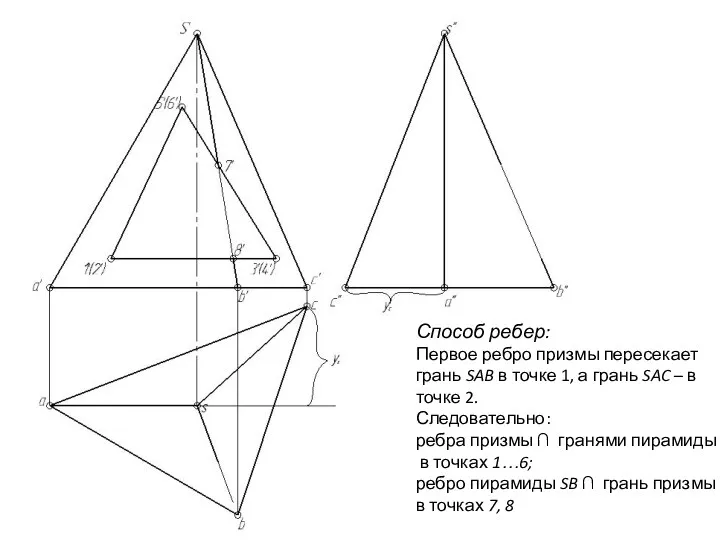
- 139. Пример: Построить пересечения поверхности пирамиды с поверхностью призмы
- 140. Способ ребер: Первое ребро призмы пересекает грань SAB в точке 1, а грань SAC – в
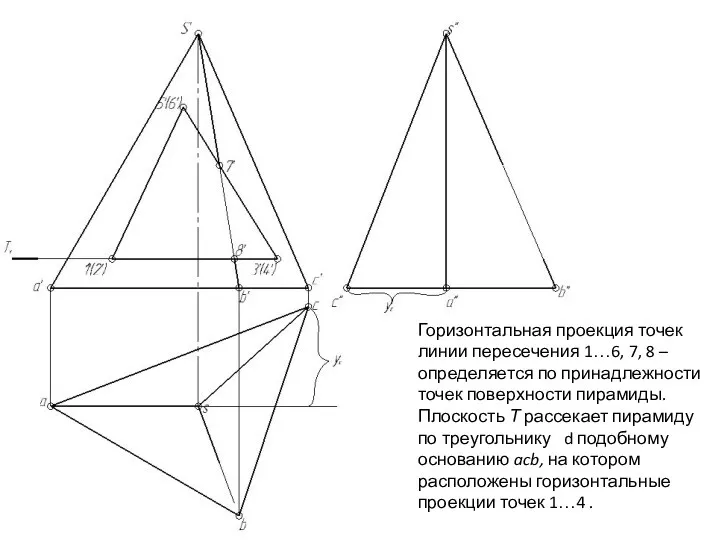
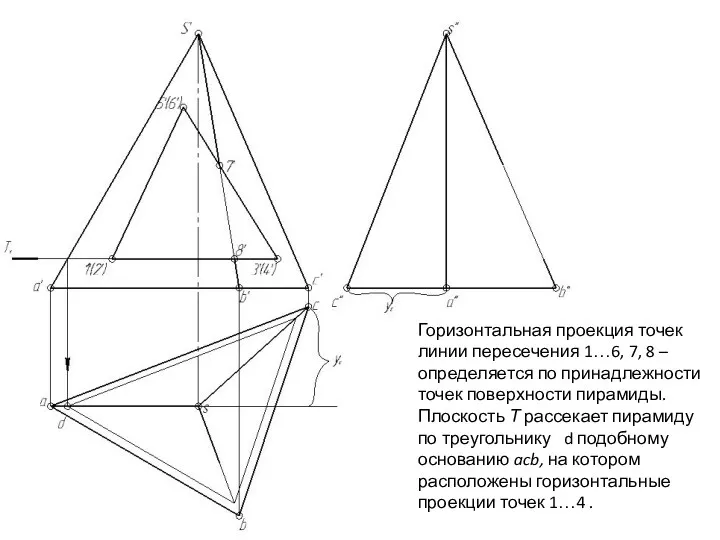
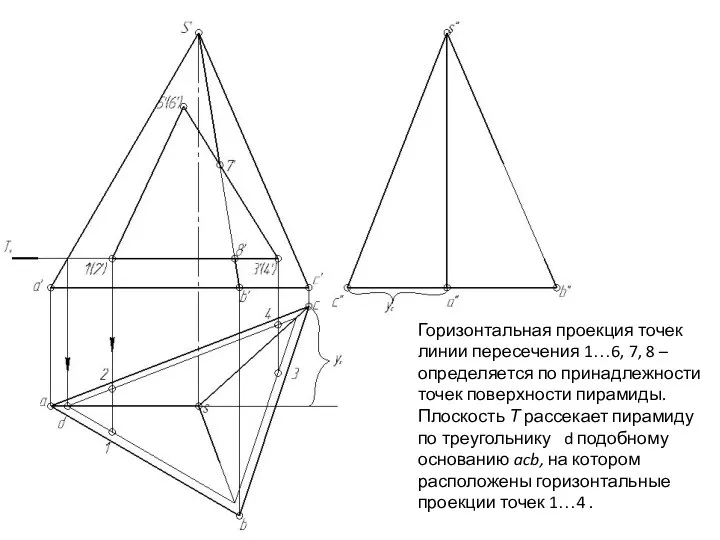
- 141. Горизонтальная проекция точек линии пересечения 1…6, 7, 8 – определяется по принадлежности точек поверхности пирамиды. Плоскость
- 142. Горизонтальная проекция точек линии пересечения 1…6, 7, 8 – определяется по принадлежности точек поверхности пирамиды. Плоскость
- 143. Горизонтальная проекция точек линии пересечения 1…6, 7, 8 – определяется по принадлежности точек поверхности пирамиды. Плоскость
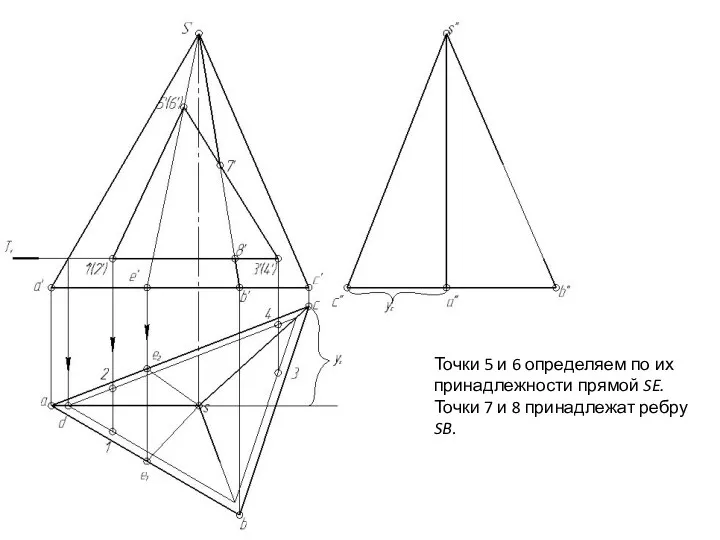
- 144. Точки 5 и 6 определяем по их принадлежности прямой SE. Точки 7 и 8 принадлежат ребру
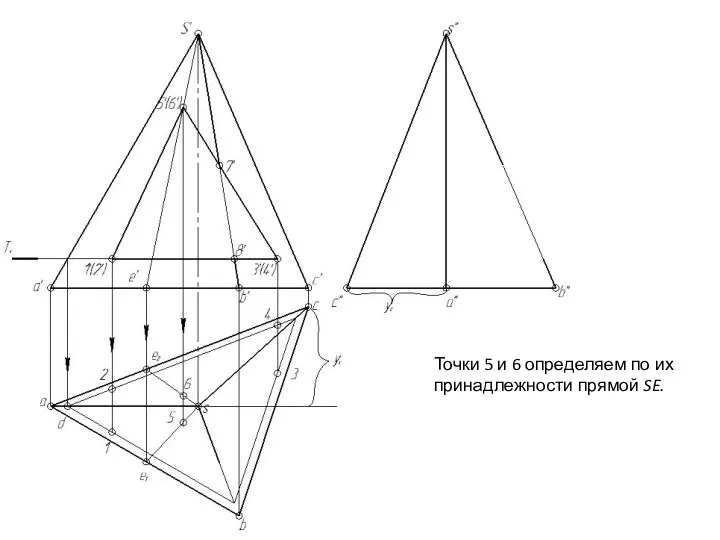
- 145. Точки 5 и 6 определяем по их принадлежности прямой SE.
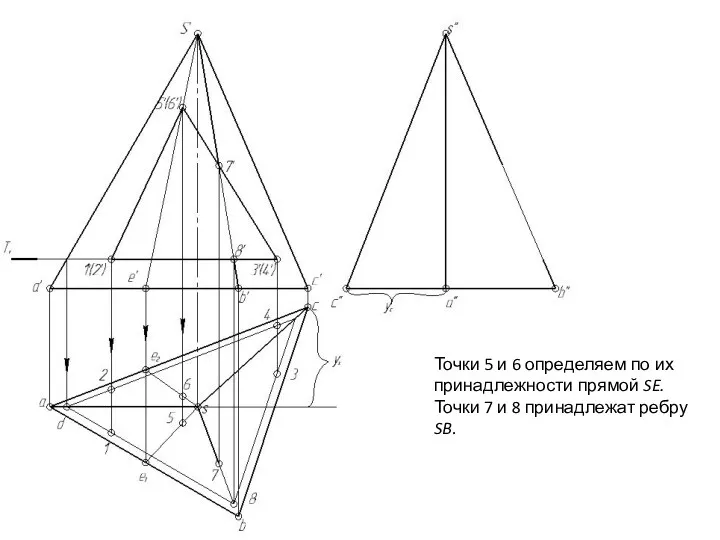
- 146. Точки 5 и 6 определяем по их принадлежности прямой SE. Точки 7 и 8 принадлежат ребру
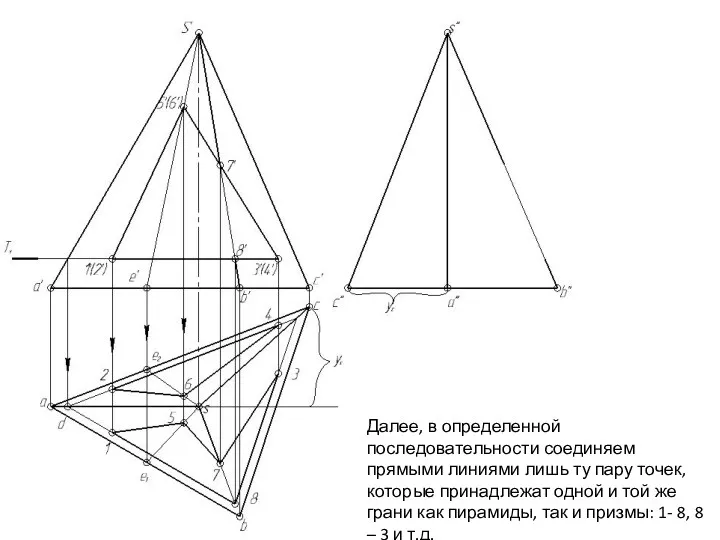
- 147. Далее, в определенной последовательности соединяем прямыми линиями лишь ту пару точек, которые принадлежат одной и той
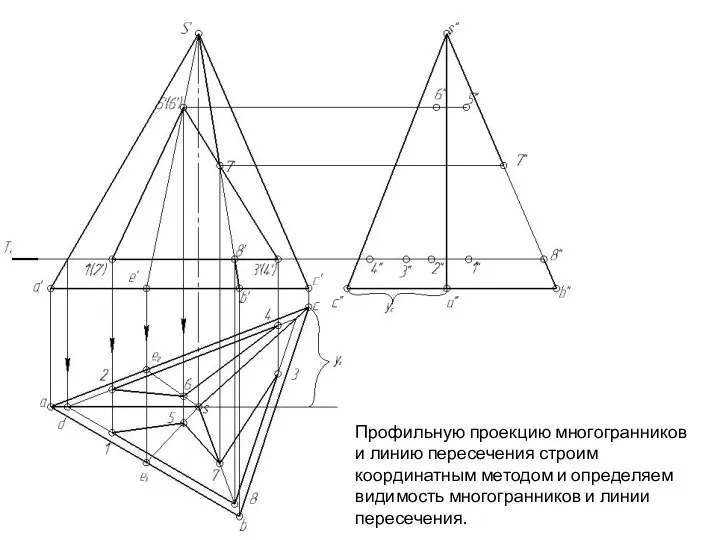
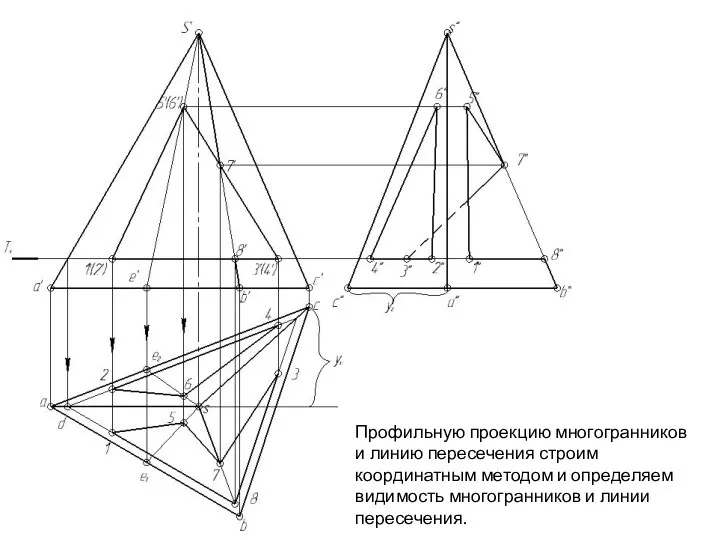
- 148. Профильную проекцию многогранников и линию пересечения строим координатным методом и определяем видимость многогранников и линии пересечения.
- 149. Профильную проекцию многогранников и линию пересечения строим координатным методом и определяем видимость многогранников и линии пересечения.
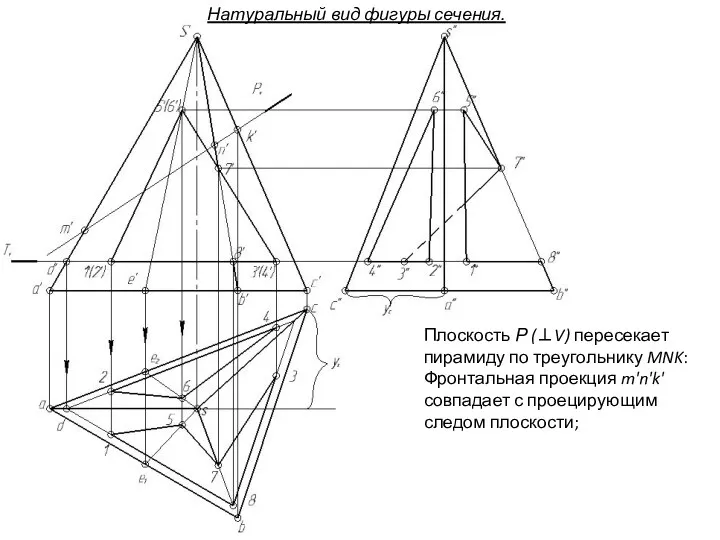
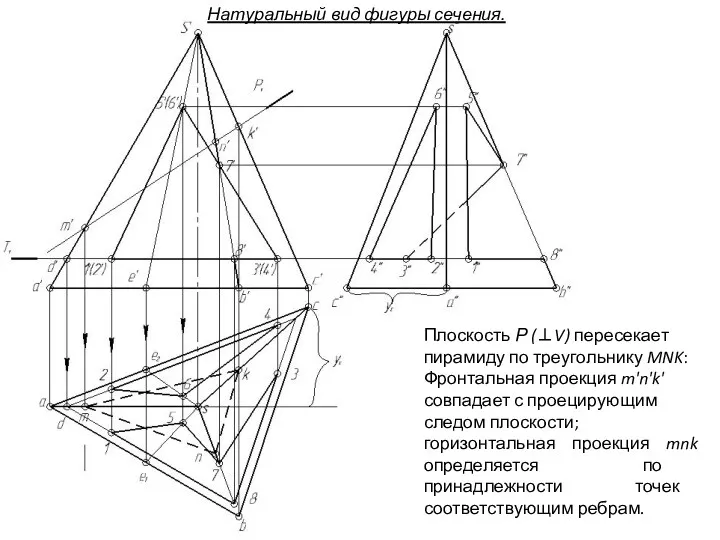
- 150. Плоскость Р (⊥V) пересекает пирамиду по треугольнику MNK: Фронтальная проекция m'n'k' совпадает с проецирующим следом плоскости;
- 151. Плоскость Р (⊥V) пересекает пирамиду по треугольнику MNK: Фронтальная проекция m'n'k' совпадает с проецирующим следом плоскости;
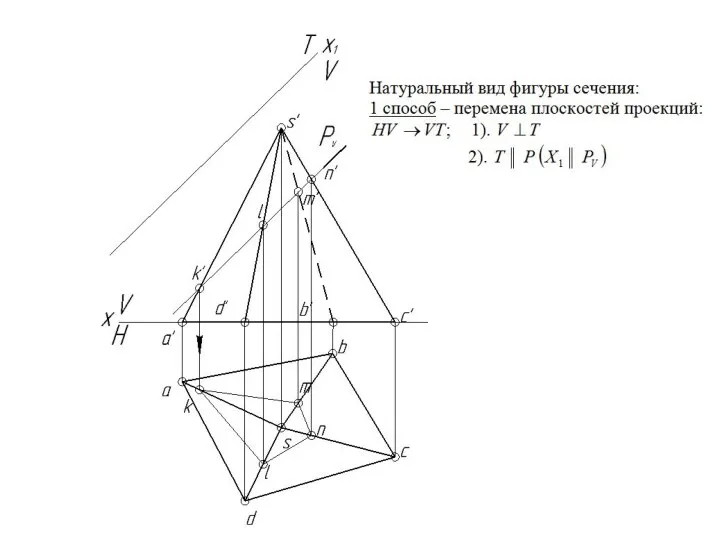
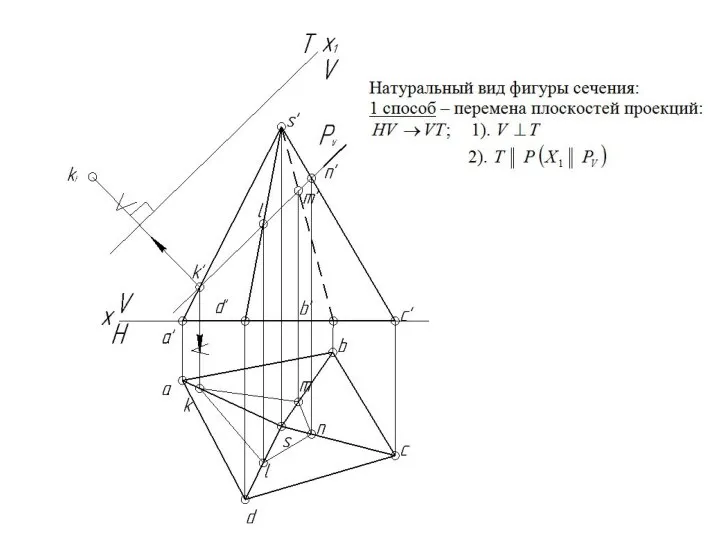
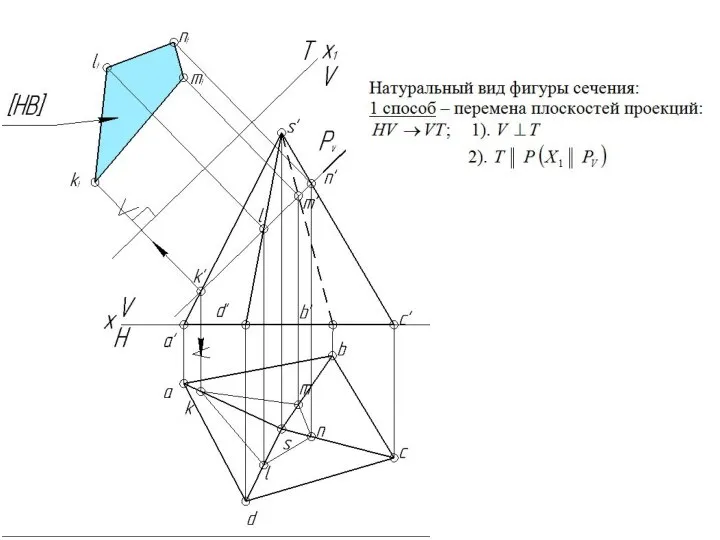
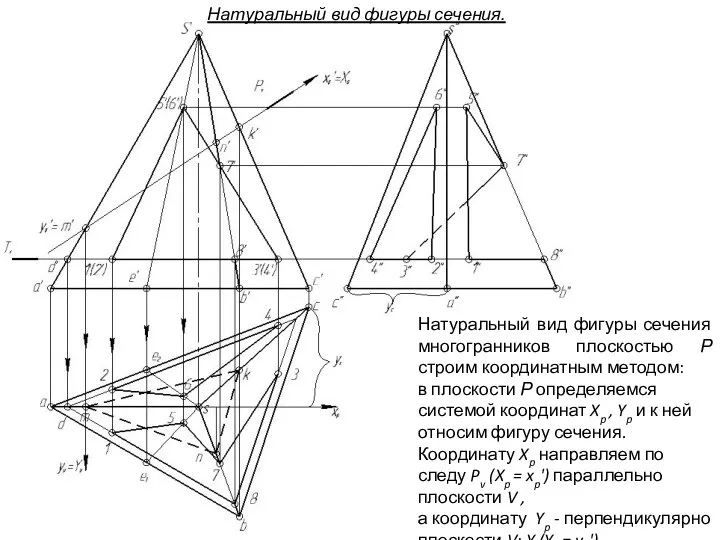
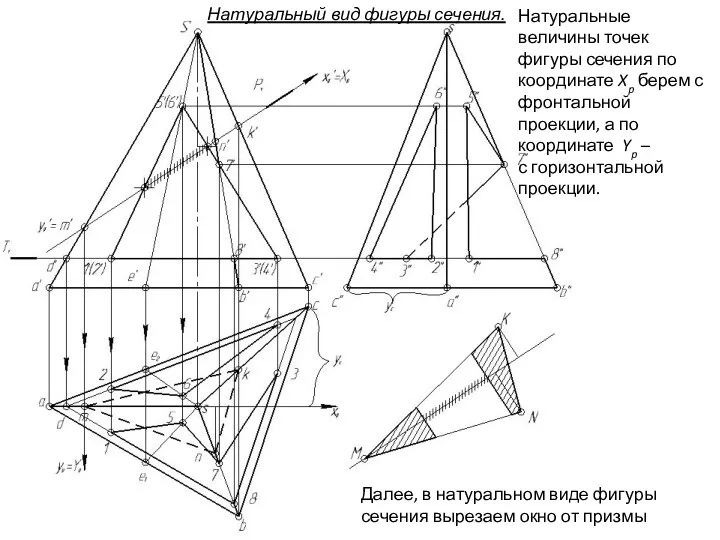
- 152. Натуральный вид фигуры сечения многогранников плоскостью Р строим координатным методом: в плоскости Р определяемся системой координат
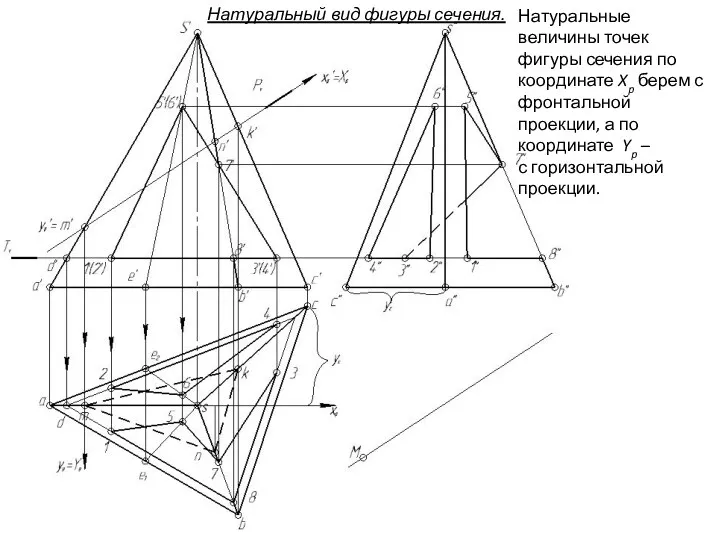
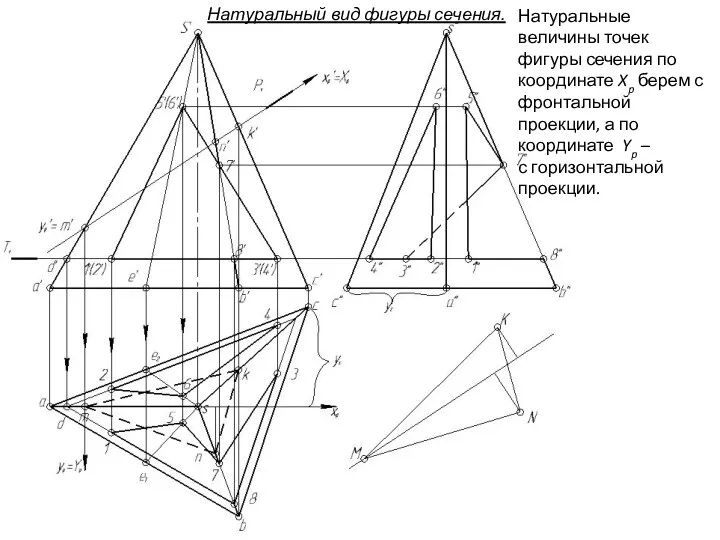
- 153. Натуральные величины точек фигуры сечения по координате Xp берем с фронтальной проекции, а по координате Yp
- 154. Натуральные величины точек фигуры сечения по координате Xp берем с фронтальной проекции, а по координате Yp
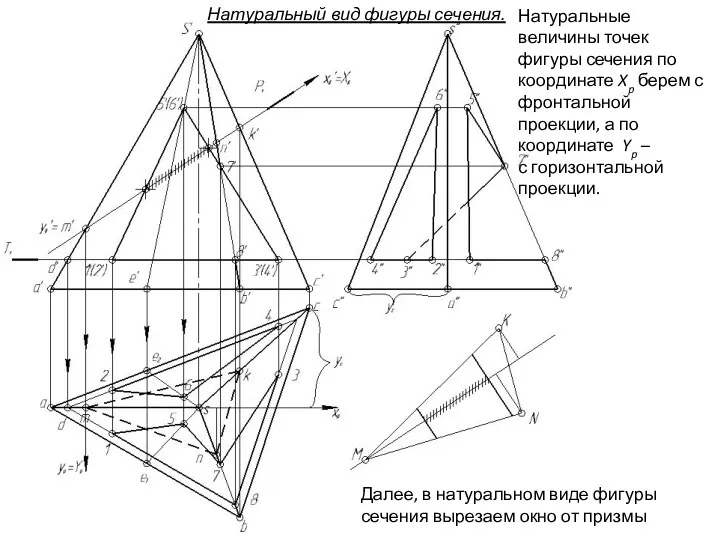
- 155. Далее, в натуральном виде фигуры сечения вырезаем окно от призмы Натуральные величины точек фигуры сечения по
- 156. Далее, в натуральном виде фигуры сечения вырезаем окно от призмы Натуральные величины точек фигуры сечения по
- 159. Скачать презентацию











 План участка контрольного пункта автосцепки (КПА) с расстановкой оборудования
План участка контрольного пункта автосцепки (КПА) с расстановкой оборудования Интерактивная компьютерная графика. Часть 5-1 (Проекции и нормали)
Интерактивная компьютерная графика. Часть 5-1 (Проекции и нормали) Обзор современных методов проектирования (Часть 2)
Обзор современных методов проектирования (Часть 2) Предмет начертательной геометрии
Предмет начертательной геометрии Курсовой проект по дисциплине Параметрическое моделирование на тему Ресторан на 220 мест
Курсовой проект по дисциплине Параметрическое моделирование на тему Ресторан на 220 мест Чертёж плоской детали, симметричной относительно одной плоскости симметрии. Алгоритм построения
Чертёж плоской детали, симметричной относительно одной плоскости симметрии. Алгоритм построения Линии чертежа по ГОСТ 2.303-68
Линии чертежа по ГОСТ 2.303-68 Восходящие и нисходящие прямые. Разбивка окружностей в перспективе. Построение перспектив методом сетки
Восходящие и нисходящие прямые. Разбивка окружностей в перспективе. Построение перспектив методом сетки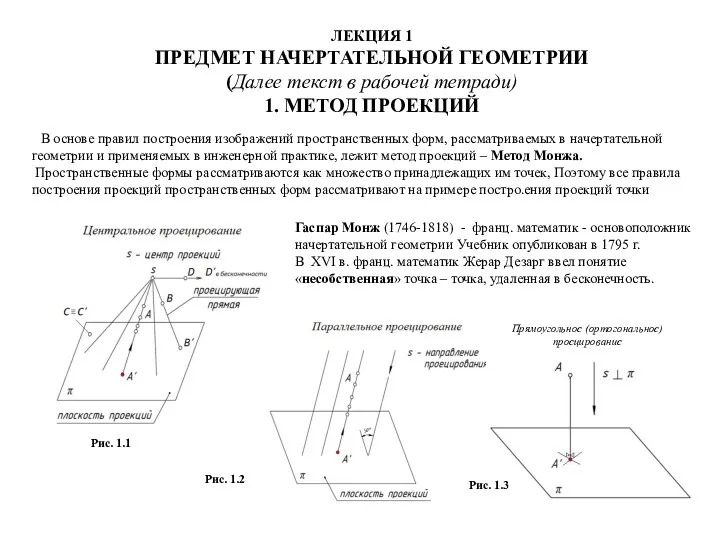 Предмет начертательной геометрии. Метод проекций
Предмет начертательной геометрии. Метод проекций Способы преобразования
Способы преобразования Изображения. Виды, разрезы, сечения
Изображения. Виды, разрезы, сечения Крепежные детали. Резьбовые соединения
Крепежные детали. Резьбовые соединения Сборочные чертежи. Разъёмные и неразъёмные соединения деталей
Сборочные чертежи. Разъёмные и неразъёмные соединения деталей Сечения
Сечения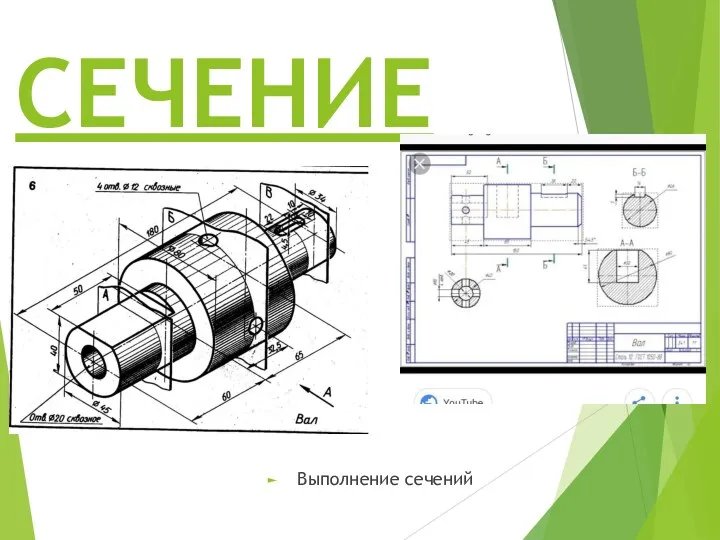 Сечение. Выполнение сечений
Сечение. Выполнение сечений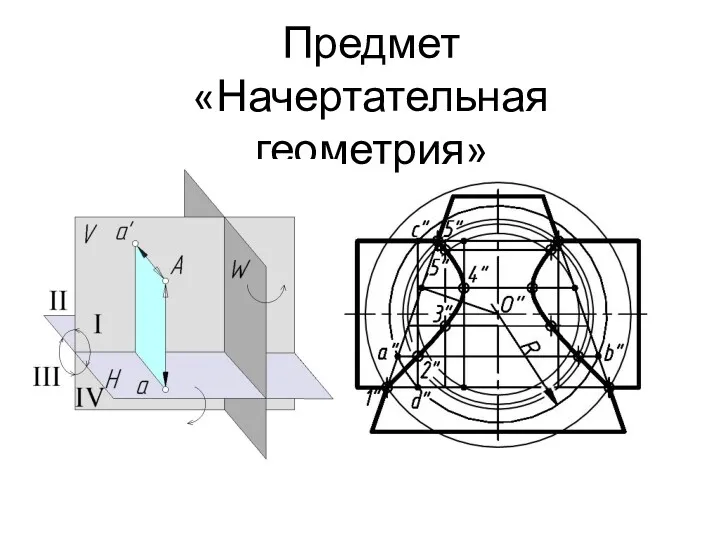 Начертательная геометрия. Лекция 01
Начертательная геометрия. Лекция 01 Правила нанесения размеров на чертежах
Правила нанесения размеров на чертежах Разрез здания. Лестница
Разрез здания. Лестница Поєднання вигляду і розрізу
Поєднання вигляду і розрізу Позиционные задачи
Позиционные задачи Ч_04.02
Ч_04.02 10_1_Сварка
10_1_Сварка Шрифт чертежный. Написание прописных и строчных букв
Шрифт чертежный. Написание прописных и строчных букв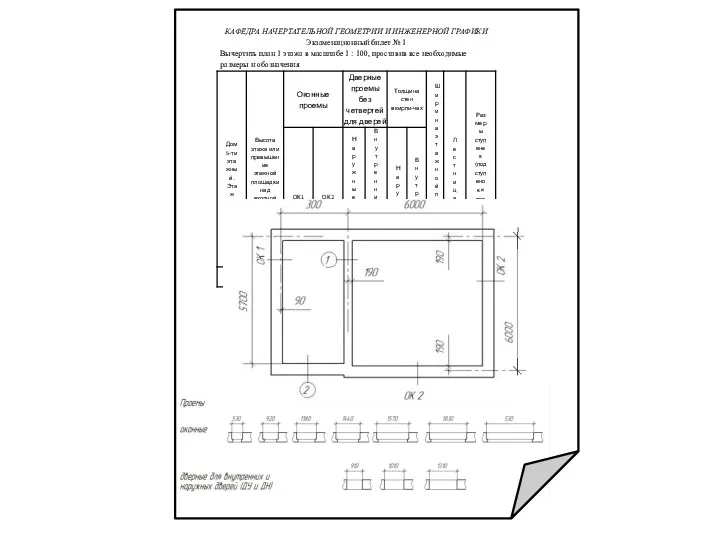 Подготовка к контрольной работе по начертательной геометрии
Подготовка к контрольной работе по начертательной геометрии Виды проецирования
Виды проецирования Составление технологической документации. 6 класс
Составление технологической документации. 6 класс Общие сведения о разрезах
Общие сведения о разрезах Чертеж - конструкторский документ
Чертеж - конструкторский документ