Содержание
- 2. ВВЕДЕНИЕ Чертеж – это своеобразный язык, с помощью которого, используя всего лишь точки, линии и ограниченное
- 3. Предмет начертательной геометрии. Начертательная геометрия – раздел геометрии. Предметом НГ является изложение и обоснование способов изображения
- 4. Образование проекций. Методы проецирования. В курсе НГ под проецированием понимается отображение пространственного образа на плоскость, которую
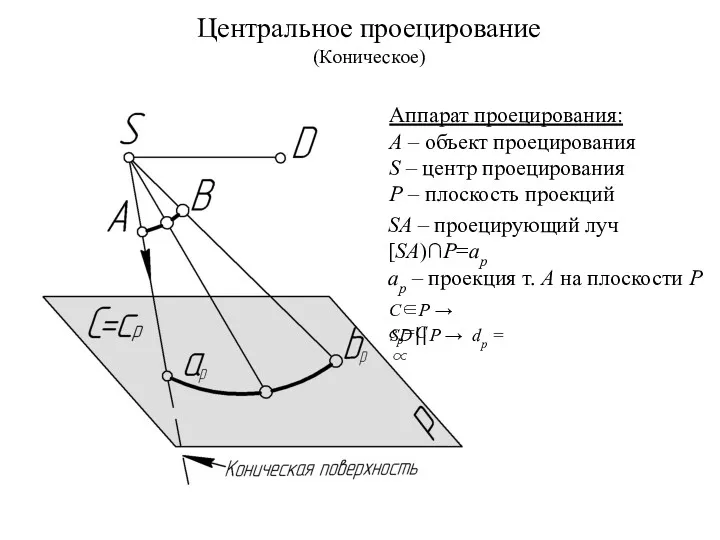
- 5. Центральное проецирование (Коническое) Аппарат проецирования: А – объект проецирования S – центр проецирования Р – плоскость
- 6. Свойства проецирования: Проекцией точки называют точку пересечения проецирующего луча с ПП. Каждая точка пространства имеет единственную
- 7. Параллельное проецирование (Цилиндрическое) (Частный случай центрального проецирования – S → ∝) Аппарат проецирования: А – объект
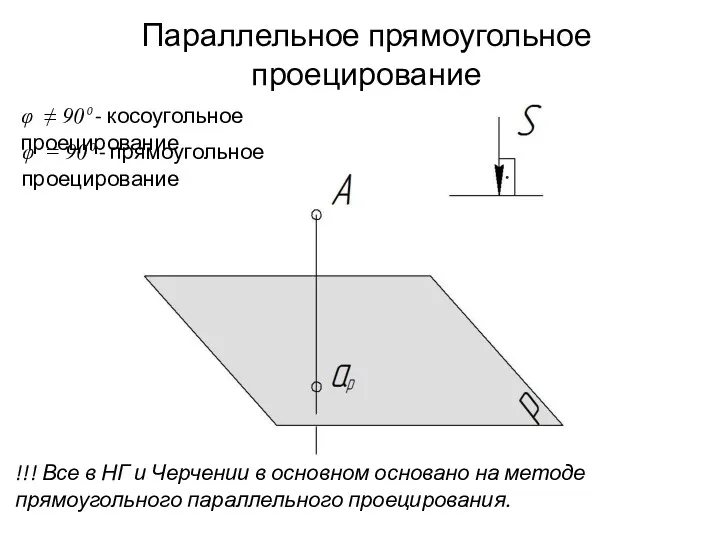
- 8. Параллельное прямоугольное проецирование φ ≠ 90⁰ - косоугольное проецирование φ = 90⁰ - прямоугольное проецирование !!!
- 9. Для получения ортогонального чертежа обладающего свойством “обратимости” необходимо иметь, по крайней мере, две связанные между собой
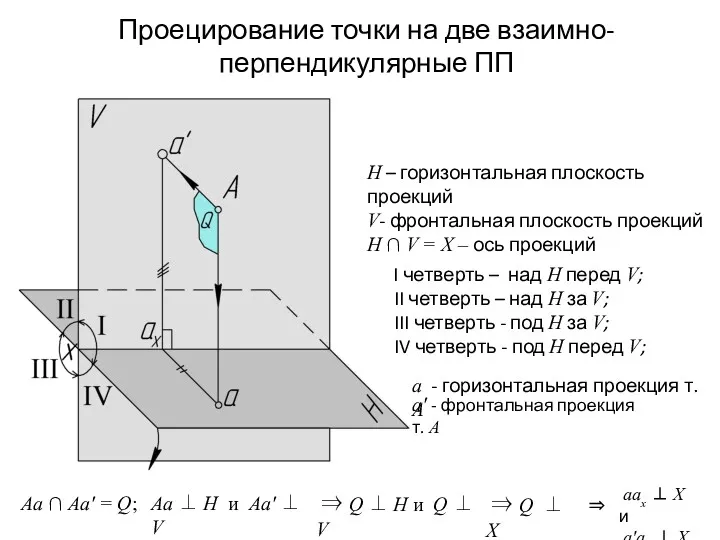
- 10. Проецирование точки на две взаимно-перпендикулярные ПП H – горизонтальная плоскость проекций V- фронтальная плоскость проекций H
- 11. Теорема: проекции некоторой точки получаются расположенными на прямых перпендикулярных к оси проекций и пересекающих эту ось
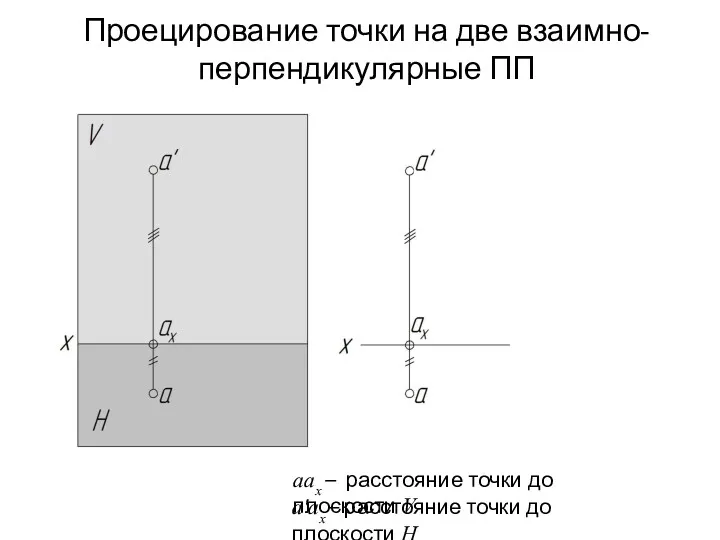
- 12. Проецирование точки на две взаимно-перпендикулярные ПП aax – расстояние точки до плоскости V a'ax – расстояние
- 13. Если восставить перпендикуляр в точке a к горизонтальной плоскости проекции, а в точке a' – к
- 14. Проецирование точки на три взаимно-перпендикулярные ПП В практике для составления чертежа изделия зачастую необходимо не две,
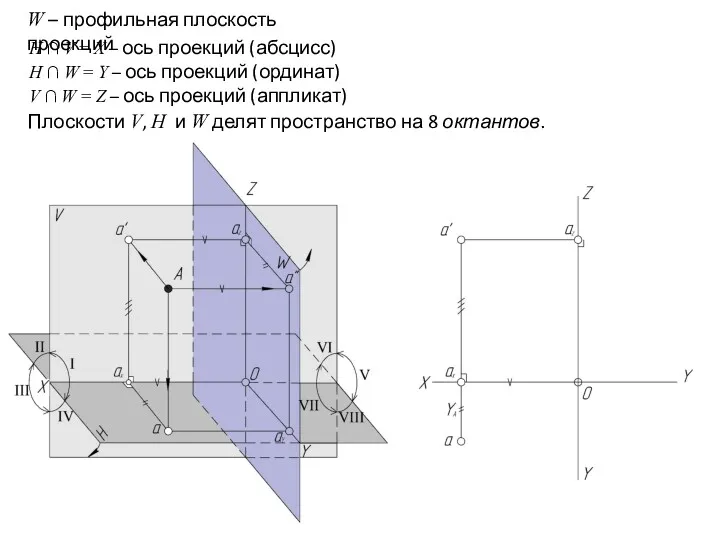
- 15. W – профильная плоскость проекций H ∩ V = X – ось проекций (абсцисс) H ∩
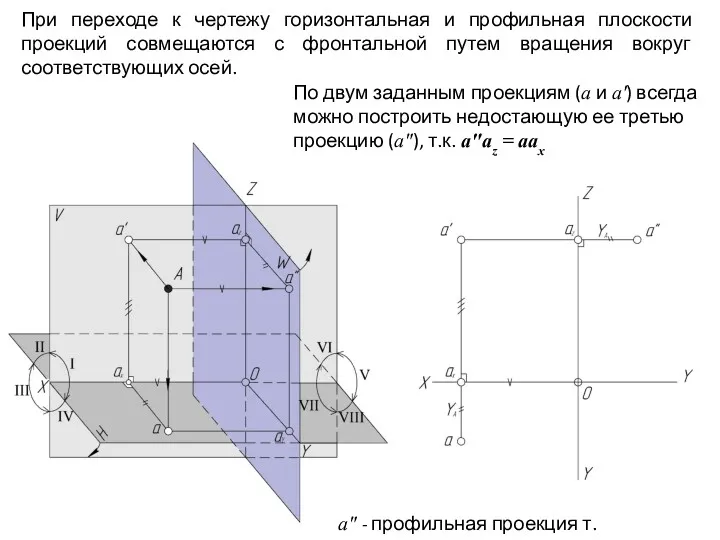
- 16. При переходе к чертежу горизонтальная и профильная плоскости проекций совмещаются с фронтальной путем вращения вокруг соответствующих
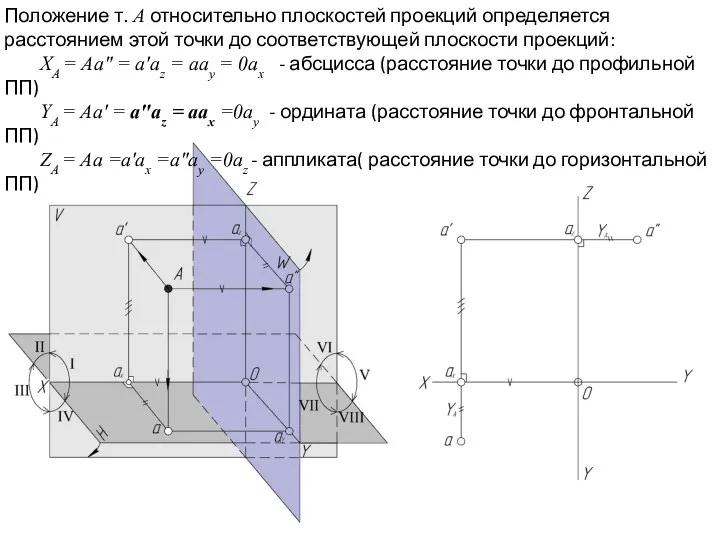
- 17. Положение т. А относительно плоскостей проекций определяется расстоянием этой точки до соответствующей плоскости проекций: XA =
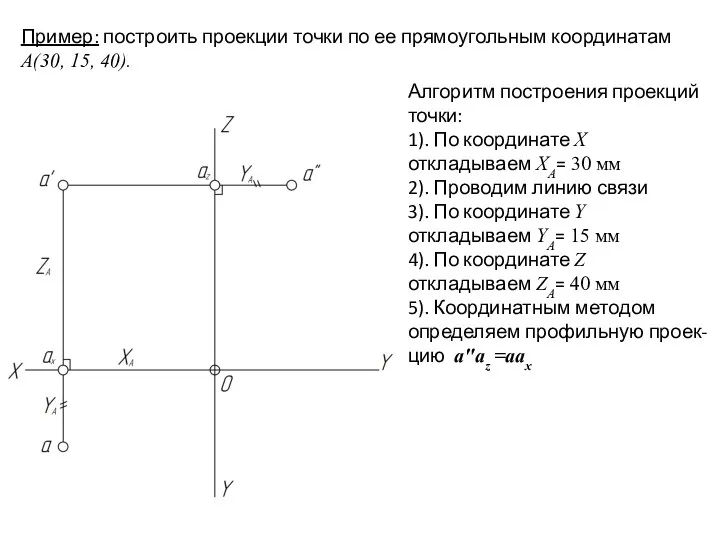
- 18. Пример: построить проекции точки по ее прямоугольным координатам А(30, 15, 40). Алгоритм построения проекций точки: 1).
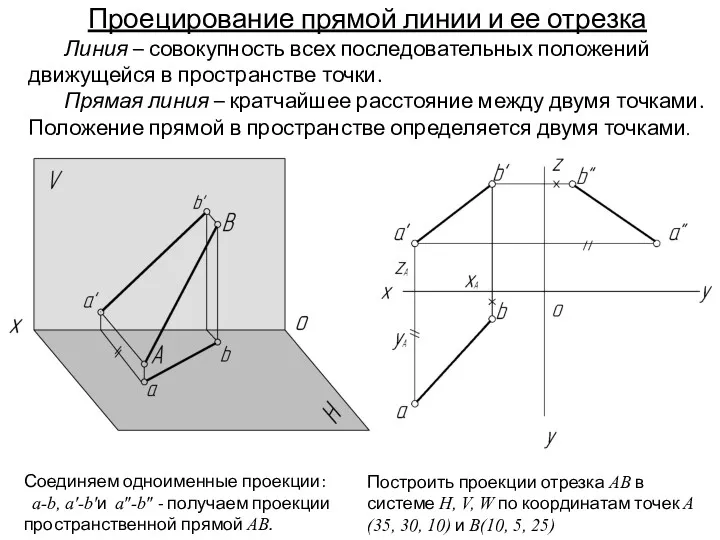
- 19. Проецирование прямой линии и ее отрезка Линия – совокупность всех последовательных положений движущейся в пространстве точки.
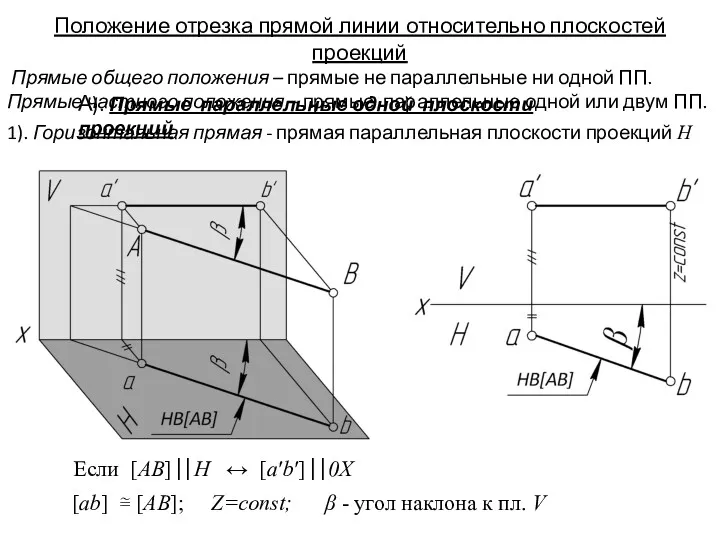
- 20. Положение отрезка прямой линии относительно плоскостей проекций Прямые общего положения – прямые не параллельные ни одной
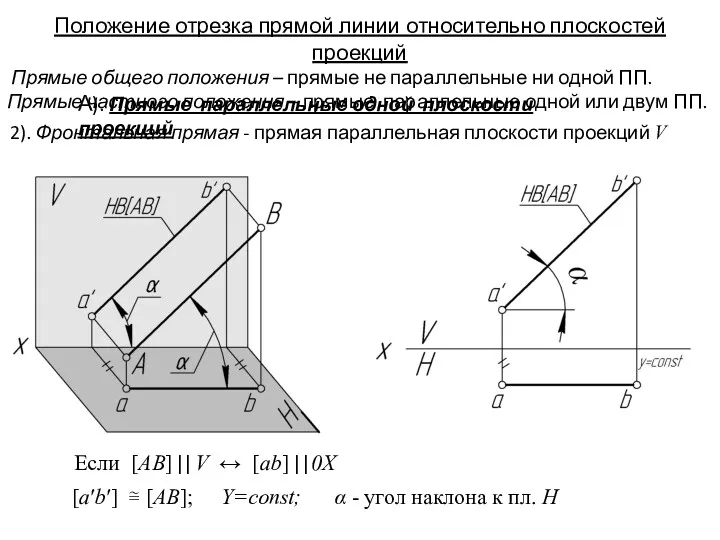
- 21. 2). Фронтальная прямая - прямая параллельная плоскости проекций V Положение отрезка прямой линии относительно плоскостей проекций
- 22. 3). Профильная прямая - прямая параллельная плоскости проекций W Положение отрезка прямой линии относительно плоскостей проекций
- 23. Положение отрезка прямой линии относительно плоскостей проекций Прямые общего положения – прямые не параллельные ни одной
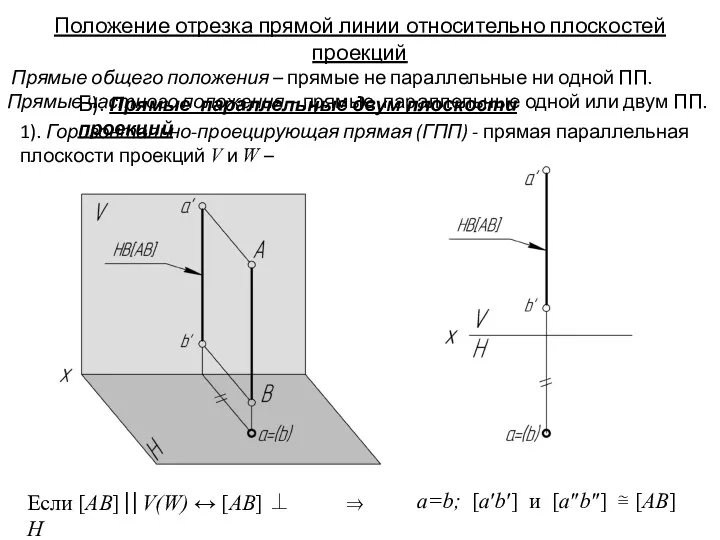
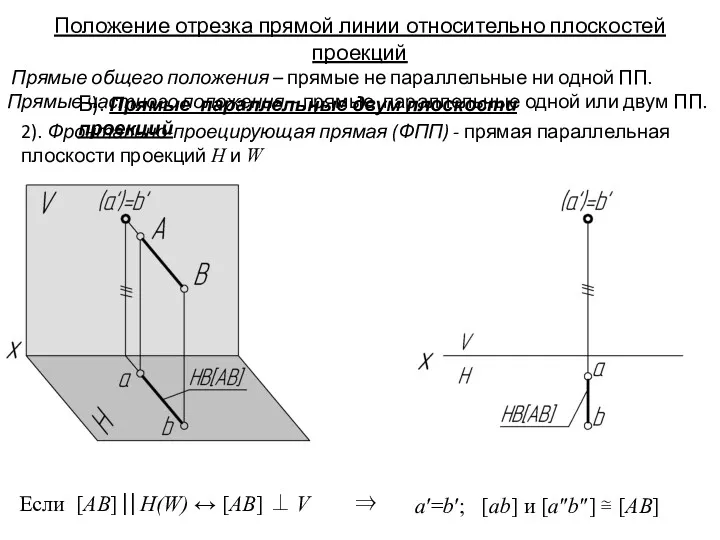
- 24. 2). Фронтально-проецирующая прямая (ФПП) - прямая параллельная плоскости проекций H и W Положение отрезка прямой линии
- 25. 3). Профильно-проецирующая прямая (ППП) - Прямая параллельная плоскости проекций H и V Положение отрезка прямой линии
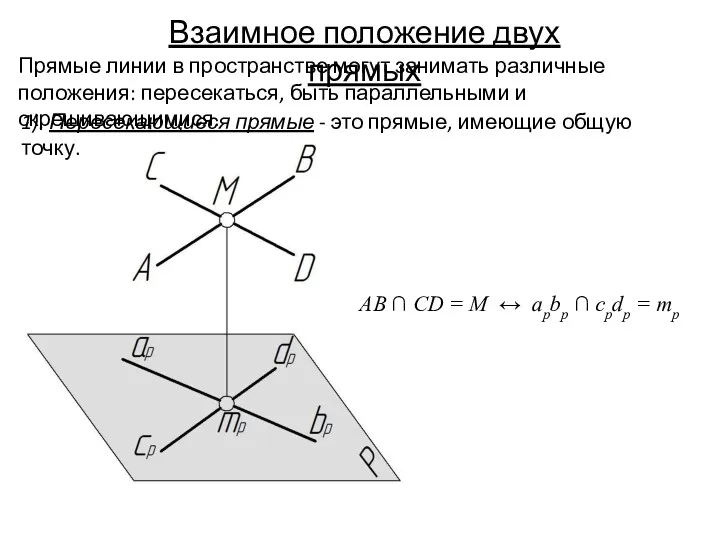
- 26. Взаимное положение двух прямых Прямые линии в пространстве могут занимать различные положения: пересекаться, быть параллельными и
- 27. Теорема: Если прямые линии пересекаются в пространстве, то на чертеже их одноименные проекции пересекаются, и точки
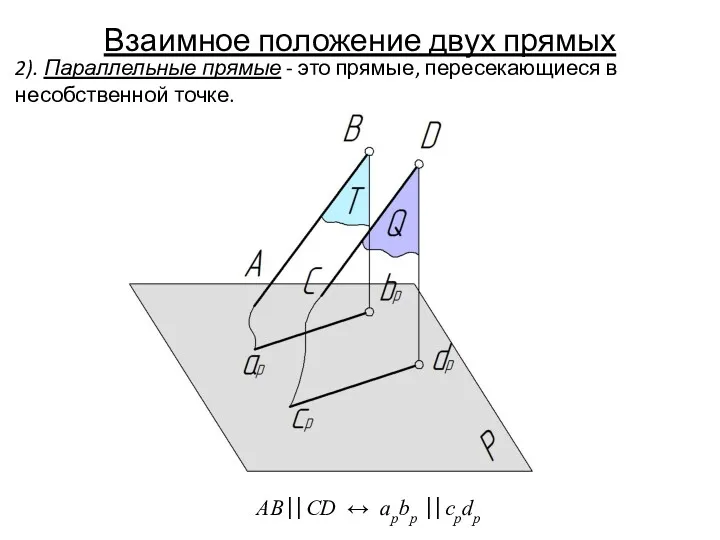
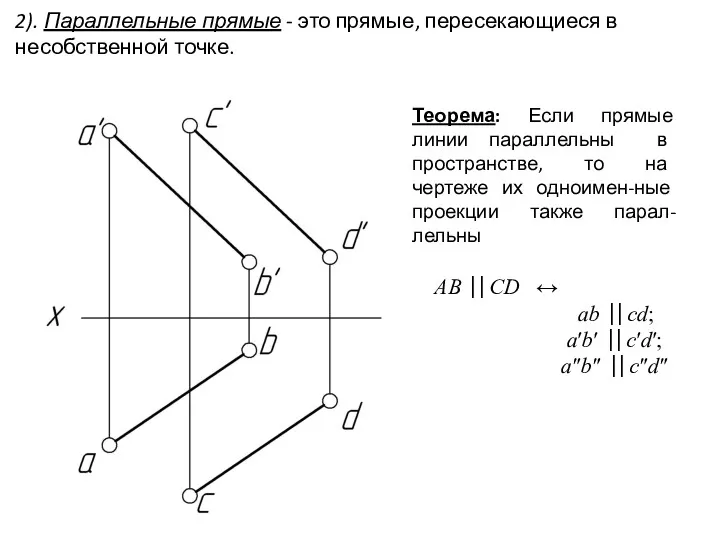
- 28. 2). Параллельные прямые - это прямые, пересекающиеся в несобственной точке. Взаимное положение двух прямых AB⎟⎟ CD
- 29. AB ⎟⎟ CD ↔ ab ⎟⎟ cd; a′b′ ⎟⎟ c′d′; a″b″ ⎟⎟ c″d″ Теорема: Если прямые
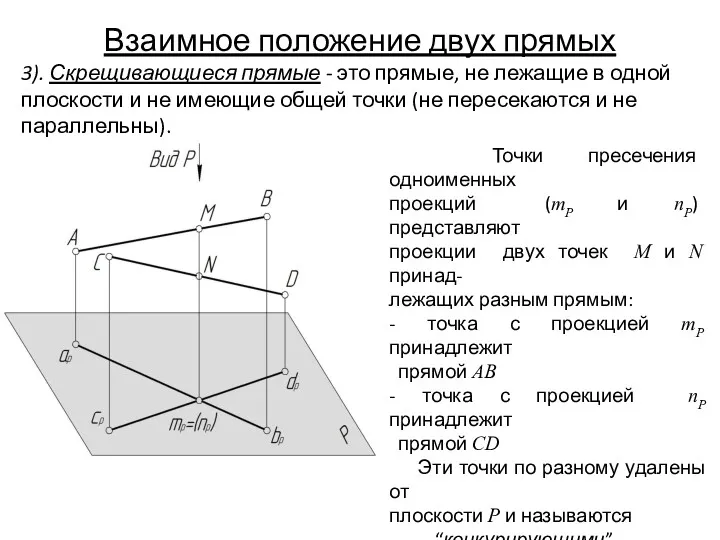
- 30. 3). Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости и не имеющие общей точки
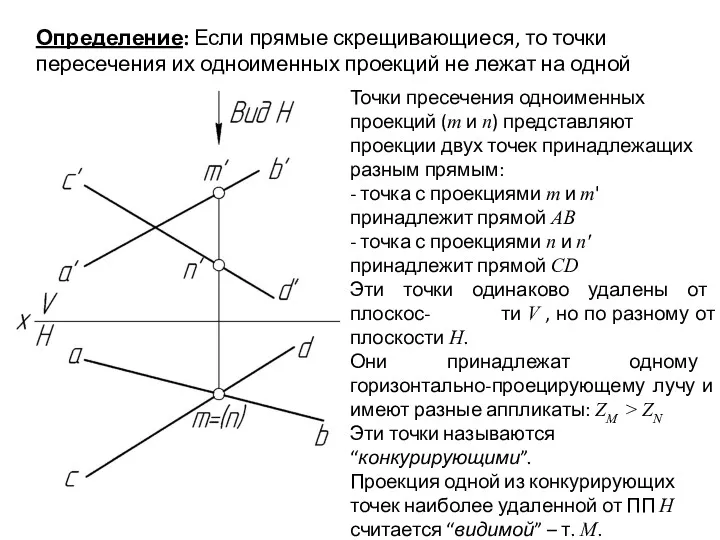
- 31. Определение: Если прямые скрещивающиеся, то точки пересечения их одноименных проекций не лежат на одной линии связи.
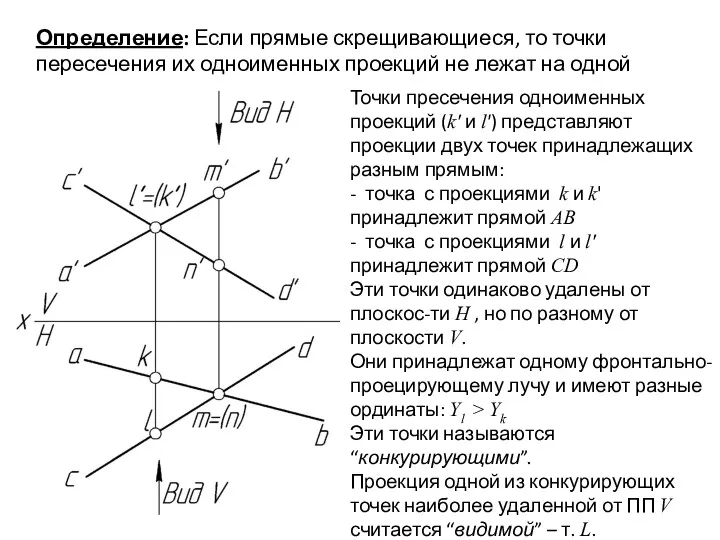
- 32. Определение: Если прямые скрещивающиеся, то точки пересечения их одноименных проекций не лежат на одной линии связи.
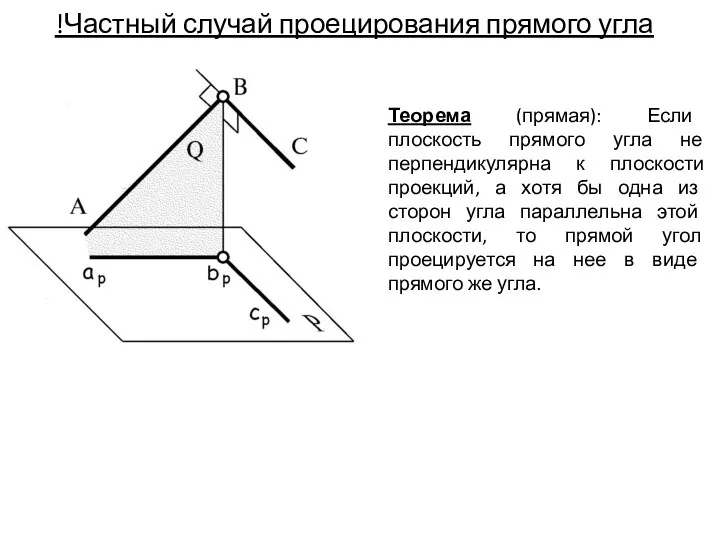
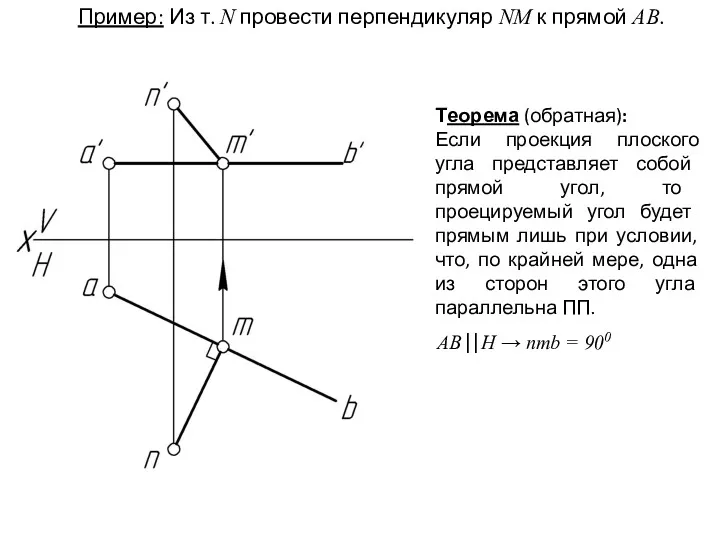
- 33. Теорема (прямая): Если плоскость прямого угла не перпендикулярна к плоскости проекций, а хотя бы одна из
- 34. Теорема (обратная): Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь
- 35. ПЛОСКОСТЬ Поверхность – совокупность всех последовательных положений движущейся в пространстве линии. В ВМ плоскость является простейшей
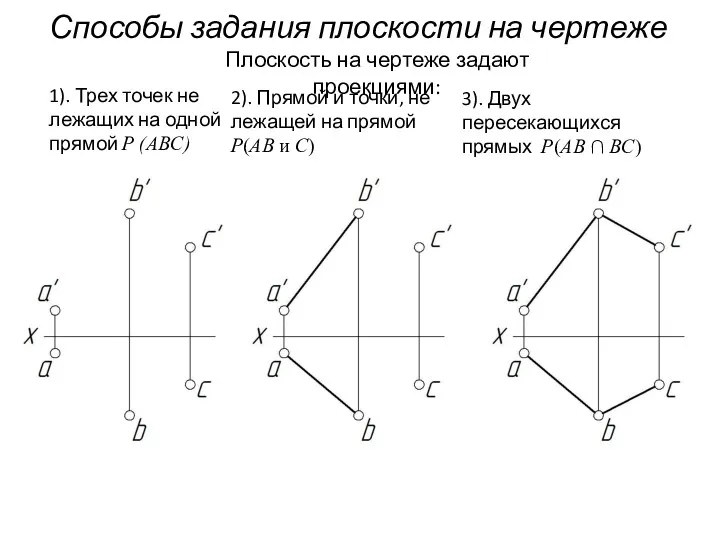
- 36. Способы задания плоскости на чертеже Плоскость на чертеже задают проекциями: 1). Трех точек не лежащих на
- 37. 4). Двух параллель-ных прямых P(AB ⎜⎜ CD) 5). Плоской фигуры P(ΔABC) 6). Следами плоскости Способы задания
- 38. Прямая и точка в плоскости Взаимное положение прямой и плоскости: I. Прямая лежит в плоскости II.Прямая
- 39. Прямая лежит в плоскости Условия принадлежности прямой плоскости: 1. Прямая принадлежит плоскости, если она проходит через
- 40. Условие принадлежности точки плоскости: Точка принадлежит плоскости, если она принадлежит прямой данной плоскости P(AB ∩ CD)
- 42. Скачать презентацию

















 Виды проецирования. Комплексный чертеж точки, плоскости
Виды проецирования. Комплексный чертеж точки, плоскости Нанесение размеров ГОСТ 2.307-68
Нанесение размеров ГОСТ 2.307-68 Изображения – виды, разрезы, сечения
Изображения – виды, разрезы, сечения Нанесение элементов водоотводящей сети на планы и разрезы здания. Составление аксонометрической схемы
Нанесение элементов водоотводящей сети на планы и разрезы здания. Составление аксонометрической схемы Плоскость. Положение плоскости в пространстве
Плоскость. Положение плоскости в пространстве Проекционное черчение. Проецирование на несколько проекций
Проекционное черчение. Проецирование на несколько проекций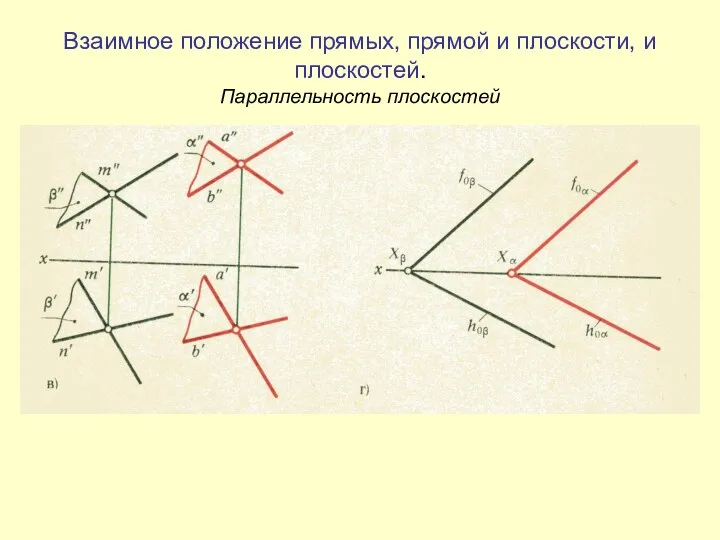 Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей
Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей Условное обозначение сварного шва
Условное обозначение сварного шва Сборочный чертеж. (14)
Сборочный чертеж. (14) Соединения деталей. Изображение разъемных и неразъемных соединений на чертежах
Соединения деталей. Изображение разъемных и неразъемных соединений на чертежах Поверхности
Поверхности Метрические задачи
Метрические задачи 20231101_aksonometricheskie_proektsii_2
20231101_aksonometricheskie_proektsii_2 Проецирование. Виды проецирования, проецирование на одну плоскость проекций
Проецирование. Виды проецирования, проецирование на одну плоскость проекций Построение перспективы интерьера (угловая перспектива) (по одной точке схода)
Построение перспективы интерьера (угловая перспектива) (по одной точке схода) Сопряжение
Сопряжение Получение аксонометрических проекций
Получение аксонометрических проекций Проецирование геометрических тел. Анализ геометрической формы
Проецирование геометрических тел. Анализ геометрической формы Основные сведения о проектировании нового строительства, реконструкции и модернизации промышленных объектов
Основные сведения о проектировании нового строительства, реконструкции и модернизации промышленных объектов اسکیس اسکیس فصل دوم
اسکیس اسکیس فصل دوم Инженерная графика. Общие правила оформления чертежей
Инженерная графика. Общие правила оформления чертежей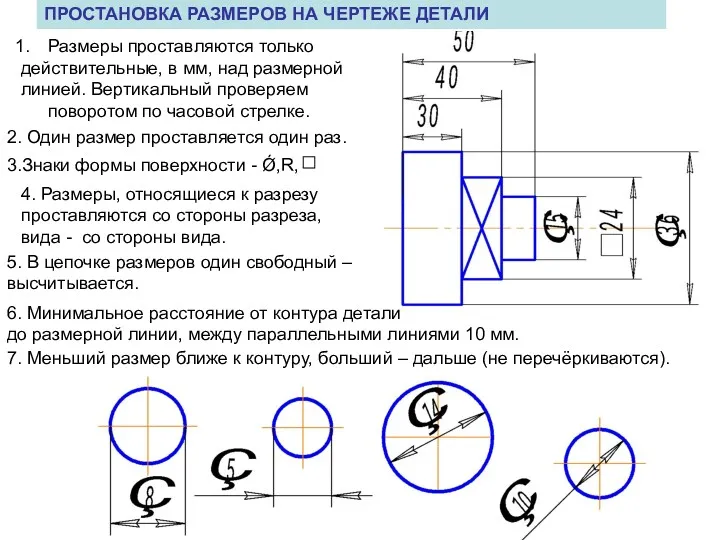 Простановка размеров на чертеже детали
Простановка размеров на чертеже детали Поверхности. Сечение поверхности плоскостью. Пересечение поверхностей
Поверхности. Сечение поверхности плоскостью. Пересечение поверхностей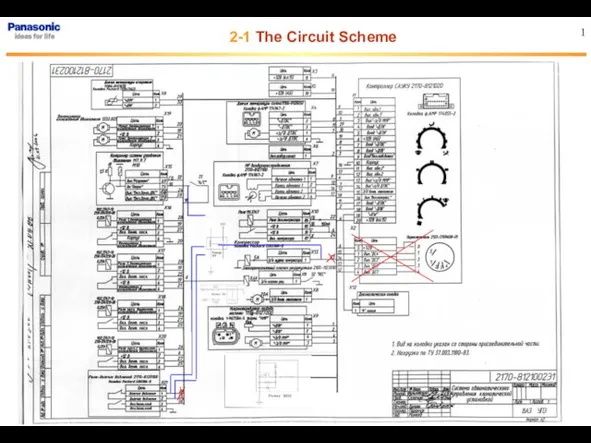 Схема климатической установки Панасоник
Схема климатической установки Панасоник Черчение. Построение циркульных и лекальных кривых
Черчение. Построение циркульных и лекальных кривых Разрезы. (Черчение. 9 класс)
Разрезы. (Черчение. 9 класс) Чертёж детали и сборочный чертёж
Чертёж детали и сборочный чертёж Положение прямой относительно плоскостей проекций
Положение прямой относительно плоскостей проекций