Содержание
- 2. Литература В.О. Гордон, М.А. Семенцов-Огиевский «Курс начертательной геометрии»; С.А. Фролов «Начертательная геометрия»; Стандарты ЕСКД; Д.В. Сорокин,
- 3. Условные обозначения Точки в пространстве – прописными буквами латинского алфавита : A, B, C,… а также
- 4. 7. Углы – строчными буквами греческого алфавита: θ, φ, ω, … 8. Проекции точек: на горизонтальную
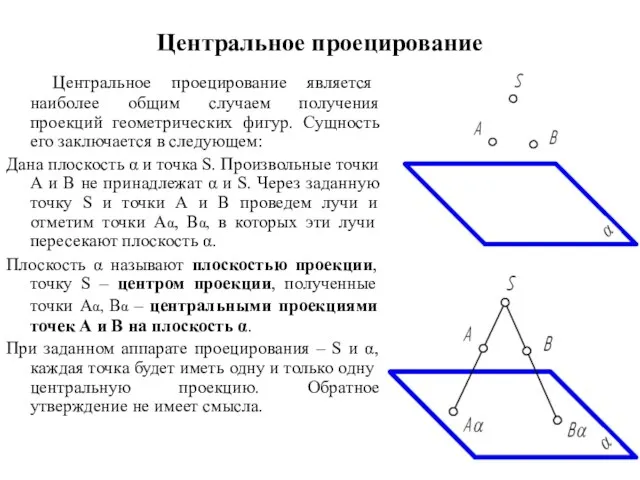
- 5. Центральное проецирование Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. Сущность его заключается в
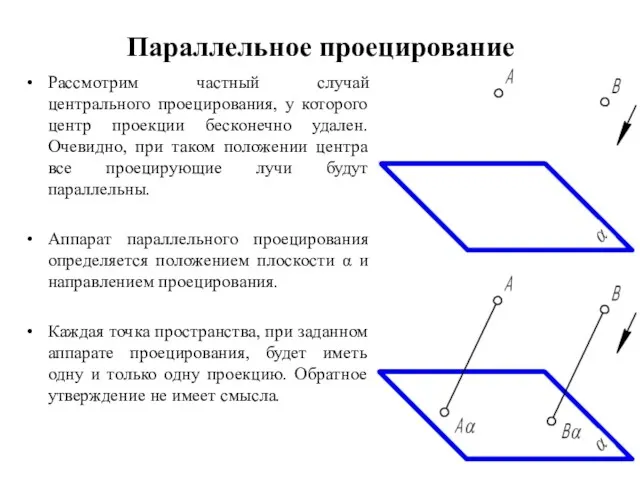
- 6. Параллельное проецирование Рассмотрим частный случай центрального проецирования, у которого центр проекции бесконечно удален. Очевидно, при таком
- 7. Основные инвариантные свойства параллельного проецирования Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажением.
- 8. 1. проекция точки есть точка; 2. проекция прямой на плоскость есть прямая; 3. если в пространстве
- 9. 5. точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых; 6. плоская фигура, параллельная
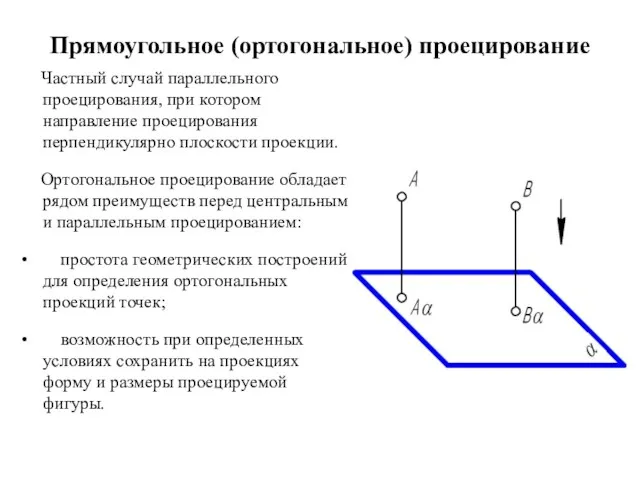
- 10. Прямоугольное (ортогональное) проецирование Частный случай параллельного проецирования, при котором направление проецирования перпендикулярно плоскости проекции. Ортогональное проецирование
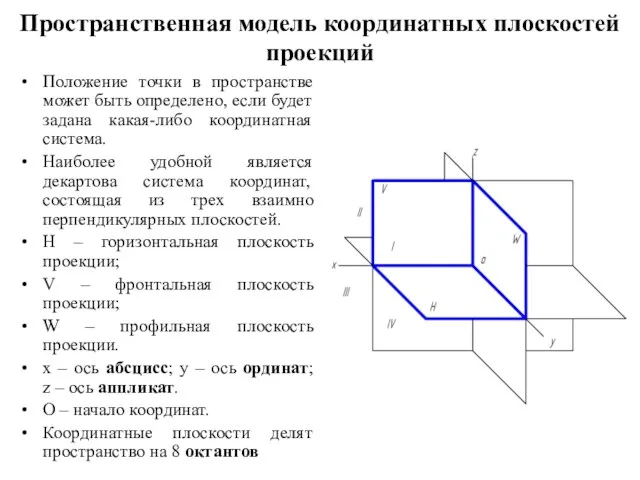
- 11. Пространственная модель координатных плоскостей проекций Положение точки в пространстве может быть определено, если будет задана какая-либо
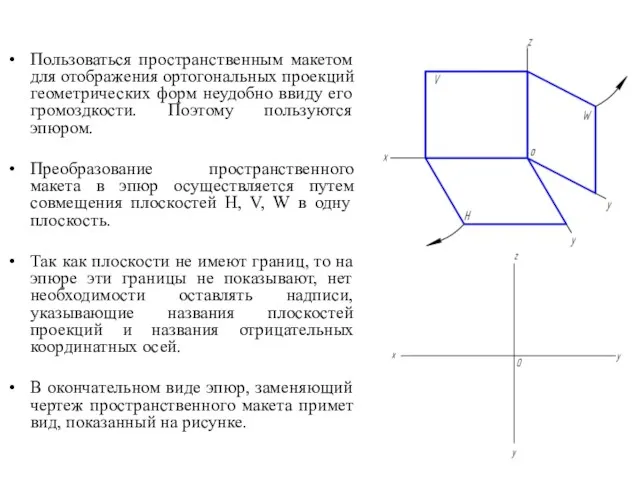
- 12. Пользоваться пространственным макетом для отображения ортогональных проекций геометрических форм неудобно ввиду его громоздкости. Поэтому пользуются эпюром.
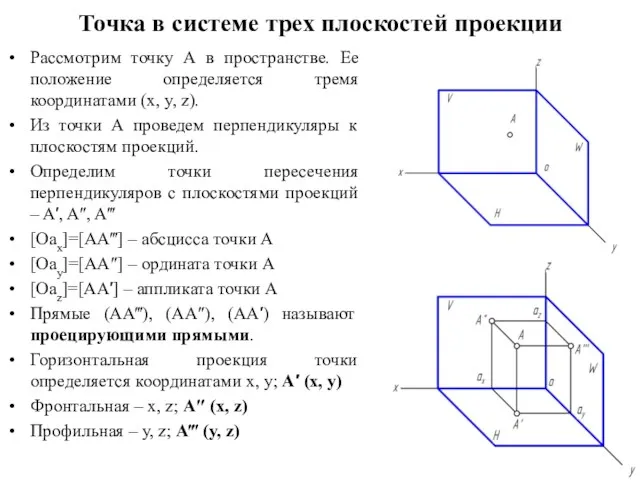
- 13. Точка в системе трех плоскостей проекции Рассмотрим точку А в пространстве. Ее положение определяется тремя координатами
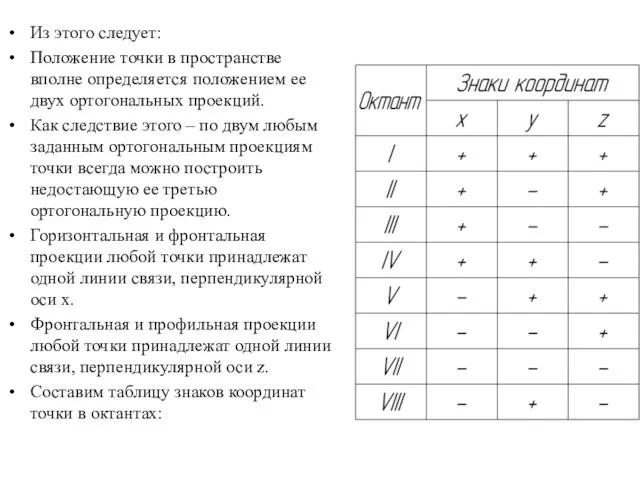
- 14. Из этого следует: Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Как следствие
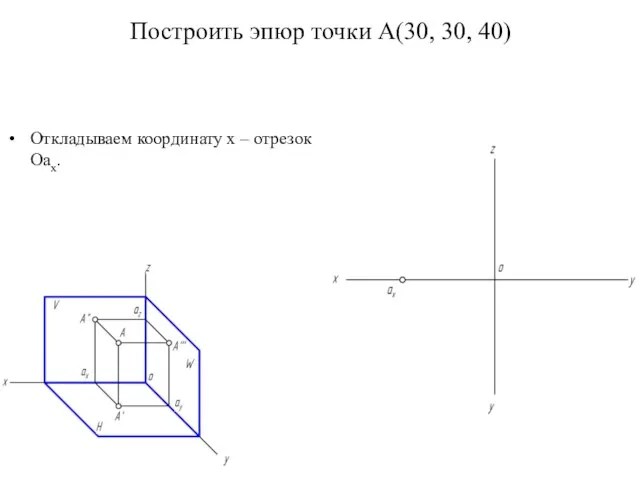
- 15. Построить эпюр точки А(30, 30, 40) Откладываем координату x – отрезок Оаx.
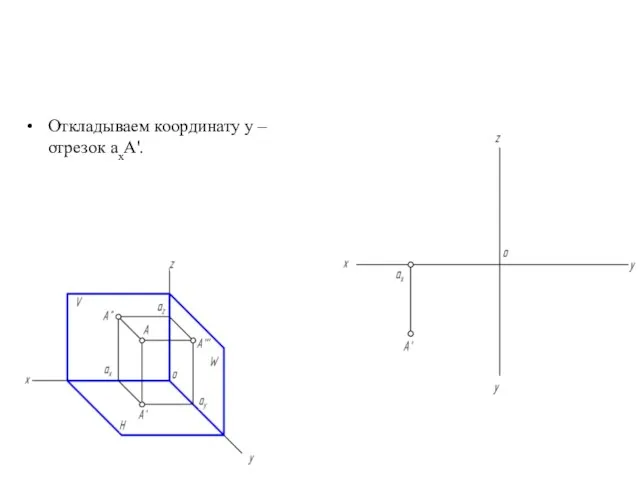
- 16. Откладываем координату y – отрезок аxA'.
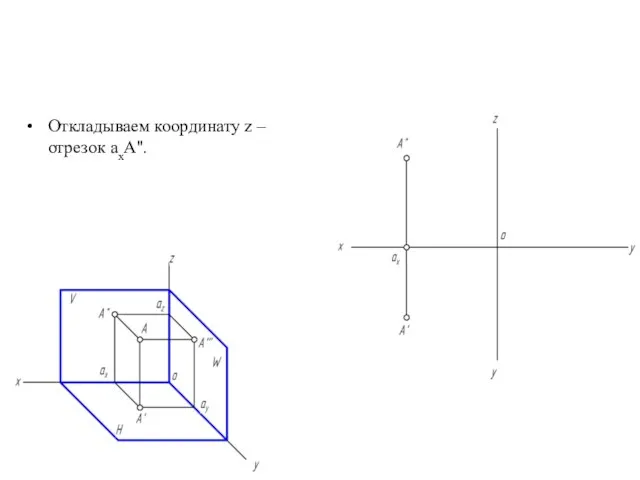
- 17. Откладываем координату z – отрезок аxA''.
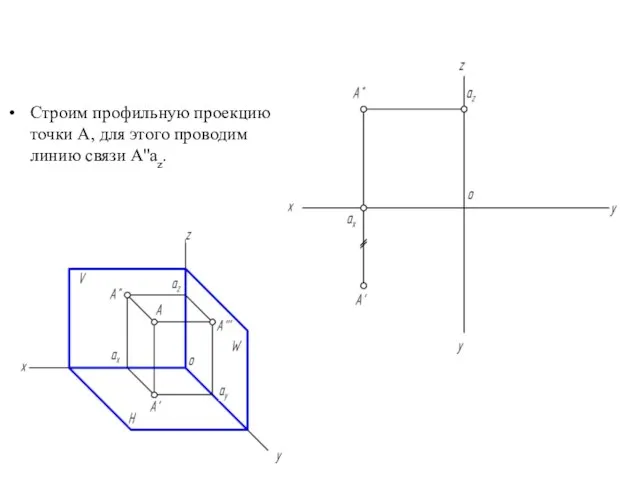
- 18. Строим профильную проекцию точки А, для этого проводим линию связи A''az.
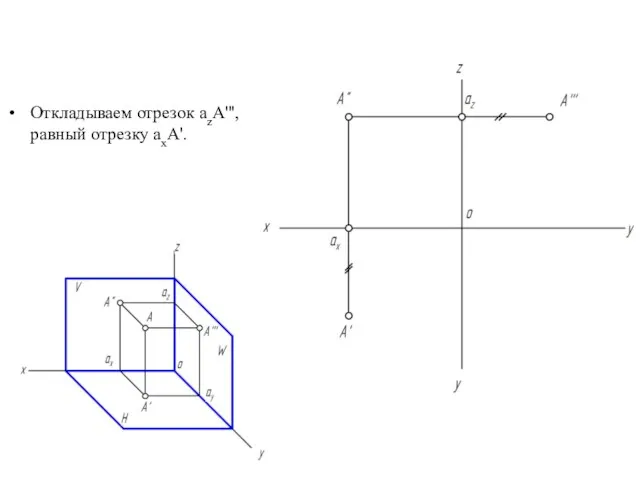
- 19. Откладываем отрезок azA''', равный отрезку axA'.
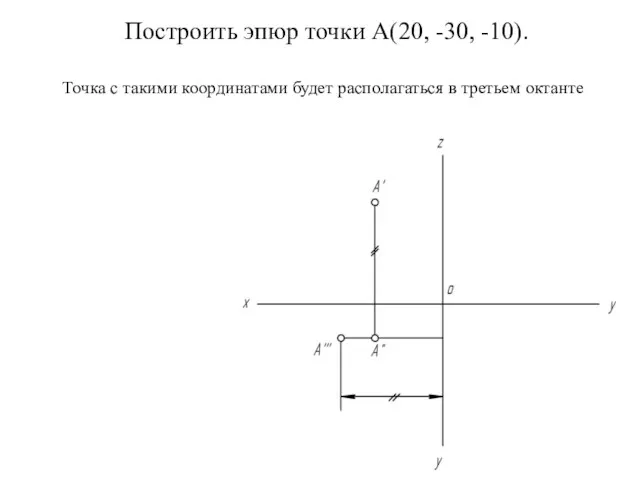
- 20. Построить эпюр точки А(20, -30, -10). Точка с такими координатами будет располагаться в третьем октанте
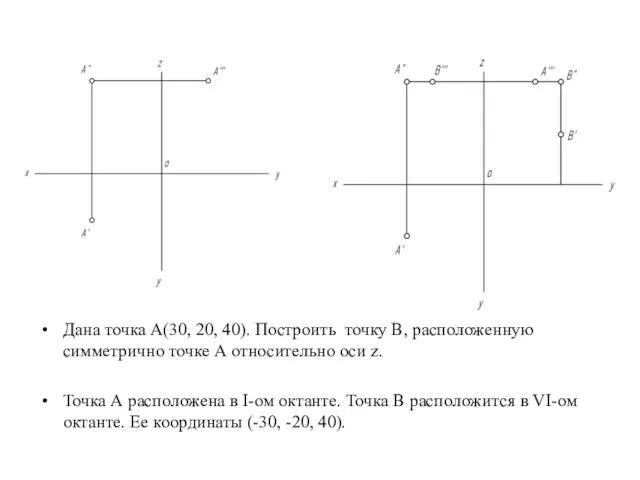
- 21. Дана точка А(30, 20, 40). Построить точку В, расположенную симметрично точке А относительно оси z. Точка
- 23. Скачать презентацию






 Стадии проектирования и состав проектов автоматизации. Виды и типы схем
Стадии проектирования и состав проектов автоматизации. Виды и типы схем Общие сведения о выполнении и оформлении рабочих чертежей деталей. Лекция 7
Общие сведения о выполнении и оформлении рабочих чертежей деталей. Лекция 7 Простановка размеров на разрезах зданий. Графические обозначения материалов, их применение в чертежах зданий и конструкций
Простановка размеров на разрезах зданий. Графические обозначения материалов, их применение в чертежах зданий и конструкций Чертежи узлов строительных конструкций
Чертежи узлов строительных конструкций Чертежи по СКГ
Чертежи по СКГ 1874 - Semiconductor Point-Contact Rectifier Effect Discovered
1874 - Semiconductor Point-Contact Rectifier Effect Discovered Математичний опис мереж зв'язку
Математичний опис мереж зв'язку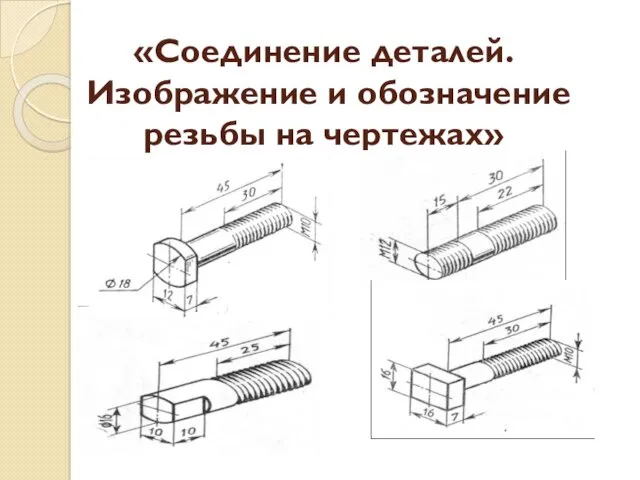 Соединение деталей. Изображение и обозначение резьбы на чертежах
Соединение деталей. Изображение и обозначение резьбы на чертежах Аксонометрические проекции. Урок 1
Аксонометрические проекции. Урок 1 Метод проекций. Эпюр Монжа. Проекции точки. Проецирование отрезка прямой линии
Метод проекций. Эпюр Монжа. Проекции точки. Проецирование отрезка прямой линии Изображения предметов. Виды, разрезы, сечения
Изображения предметов. Виды, разрезы, сечения Сбоpочный чеpтеж и спецификация сборочной единицы
Сбоpочный чеpтеж и спецификация сборочной единицы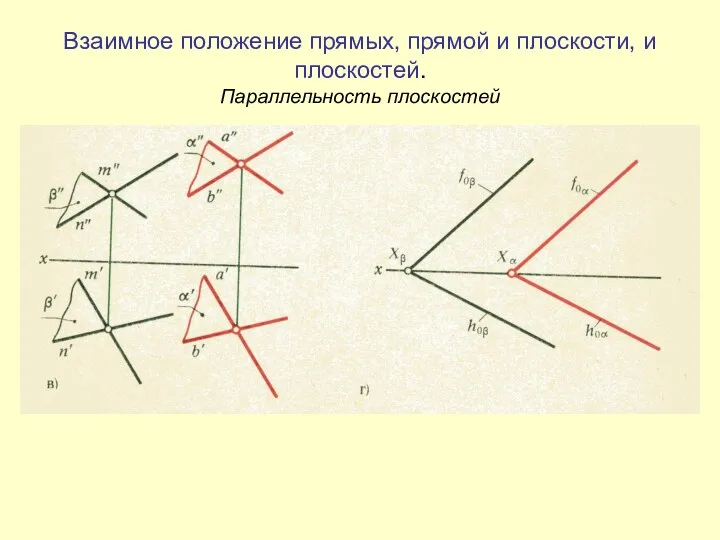 Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей
Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей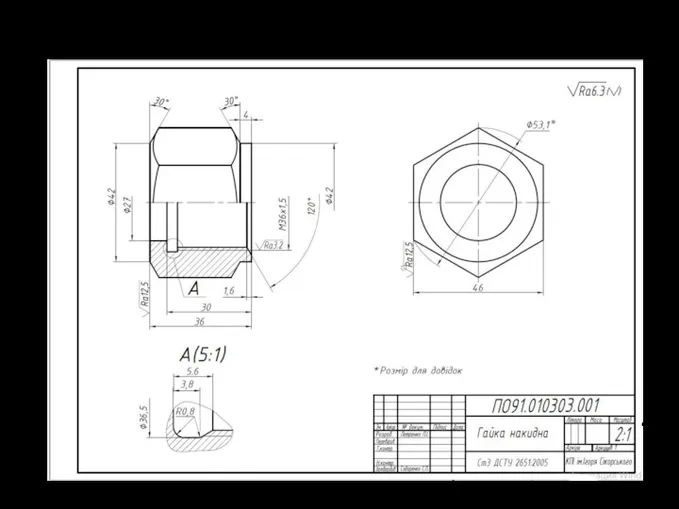 Аудиторна графічна робота Гайка накидна
Аудиторна графічна робота Гайка накидна Геометрические построения
Геометрические построения Поверхности. Основные понятия и определения
Поверхности. Основные понятия и определения Аксонометрические проекции. Получение аксонометрических проекций
Аксонометрические проекции. Получение аксонометрических проекций Спецификация
Спецификация Инженерная графика. Резьба
Инженерная графика. Резьба Деталирование
Деталирование Развертки поверхностей
Развертки поверхностей Строительное черчение. Графическое оформление и чтение строительных чертежей
Строительное черчение. Графическое оформление и чтение строительных чертежей Поверхности. Лекция 4
Поверхности. Лекция 4 Особые случаи разрезов
Особые случаи разрезов Рабочий чертёж
Рабочий чертёж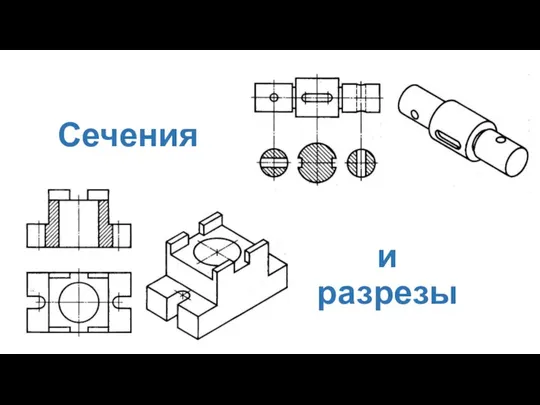 Сечения и разрезы
Сечения и разрезы Проекционное черчение. Методы проецирования
Проекционное черчение. Методы проецирования Построение окружностей и тел вращения в перспективе
Построение окружностей и тел вращения в перспективе