Содержание
- 2. Задание поверхности на чертеже 2. Определителем – совокупностью геометрических элементов, позволяющих реализовать закон образования поверхности 1.
- 3. Каркасный способ задания поверхности Каркас поверхности – упорядоченное множество точек или линий, принадлежащих поверхности. Если поверхность
- 4. Кинематический способ образования поверхностей Поверхность – непрерывная совокупность последовательных положений линии gj , перемещающейся в пространстве
- 5. Определитель поверхности Определитель поверхности – необходимая и достаточная совокупность независимых условий, однозначно задающих поверхность. Ф (Г);
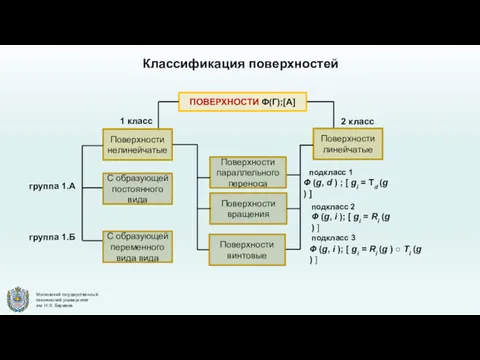
- 6. Классификация поверхностей 1 класс 2 класс группа 1.А группа 1.Б подкласс 1 подкласс 2 подкласс 3
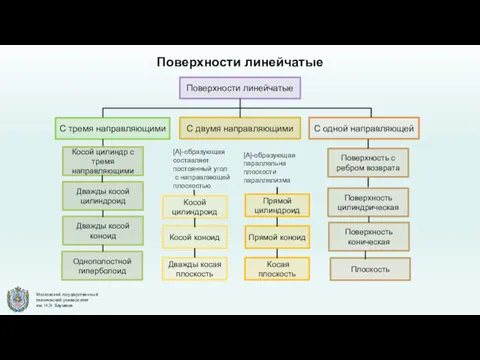
- 7. Поверхности линейчатые Поверхности линейчатые С тремя направляющими С одной направляющей С двумя направляющими Косой цилиндр с
- 8. Линейчатые поверхности с тремя направляющими Дважды косой цилиндроид Косой цилиндр с тремя направляющими Однополостной гиперболоид Дважды
- 9. Линейчатые поверхности с двумя направляющими и направляющей плоскостью Ф ( g, d1 , d2 , α
- 10. Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана) g ║ α Ф ( g,
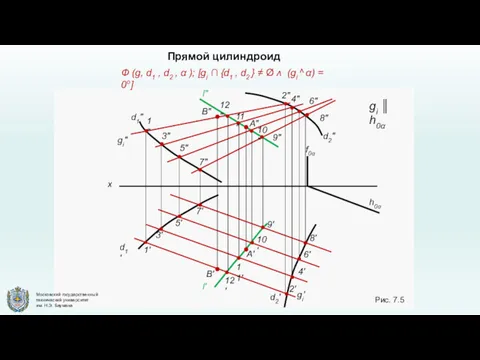
- 11. 2" 1' 2' 3' 4' 5' 6' 7' 8' 9' 10' 11' 12' 4" 6" 8"
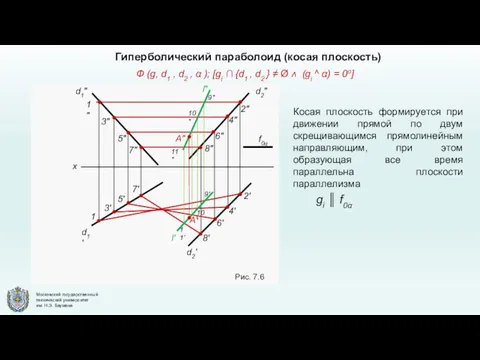
- 12. Гиперболический параболоид (косая плоскость) Косая плоскость формируется при движении прямой по двум скрещивающимся прямолинейным направляющим, при
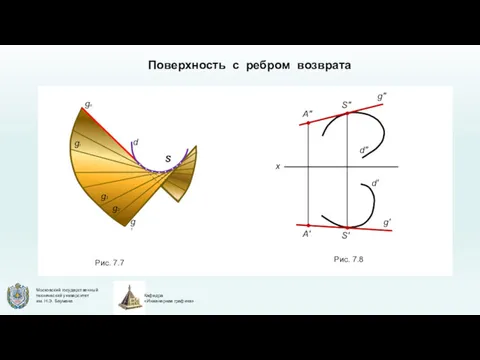
- 13. Линейчатые поверхности с одной направляющей (торсовые поверхности) Поверхность с ребром возврата (торс) образуется перемещением прямолинейной образующей
- 14. Si gi g1 g2 g3 gn d Поверхность с ребром возврата d' d" A" S" g"
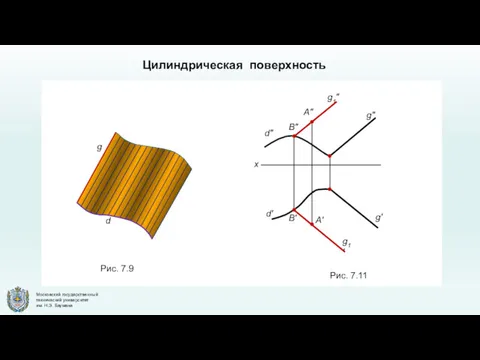
- 15. Цилиндрическая поверхность g' g" A' B' g1' d' d" B" A" g1" d g Рис. 7.9
- 16. Коническая поверхность A" B" S" g" A' B' g' S g d d" x S' d'
- 17. Подклассы поверхностей Движение образующей g может быть задано: направляющими линиями d законом движения поступательным вращательным винтовым
- 18. Поверхности вращения - образуются при вращении образующей g (прямой или кривой) вокруг неподвижной оси вращения i
- 19. Вращение – перемещение точки по окружности в плоскости, перпендикулярной оси вращения. Пересечение плоскости вращения с осью
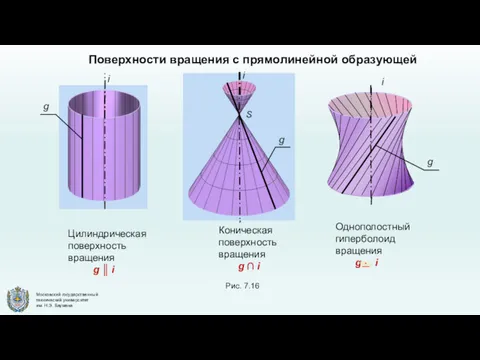
- 20. Поверхности вращения с прямолинейной образующей Коническая поверхность вращения g ∩ i Однополостный гиперболоид вращения g i
- 21. Цилиндрическая поверхность Ф ( i, ℓ, m ); [ ℓ ∩ m ≠ Ø; ℓ ║i
- 22. Ф ( i, ℓ, m, S ); [ ℓ ∩ m ≠ Ø; ℓ ∩ i
- 23. Поверхности вращения с образующей окружностью При вращении окружности вокруг ее диаметра образуется сфера Тор – поверхность,
- 24. Торовые поверхности r r > R r = R Открытый тор Закрытый тор Самопересекающийся тор Рис.
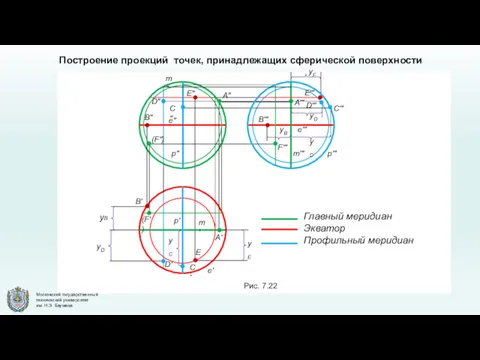
- 25. Главный меридиан Экватор Профильный меридиан e' m' p' B' E' yB yB p" e" B" E"
- 26. Построение проекций точек, принадлежащих торовой поверхности A" (B") 1" 2" c1" c2" A' B' 1' 2'
- 27. i' Поверхности вращения с образующей кривой второго порядка эллипс A" g" i" A' g' x i
- 28. Поверхности вращения с образующей кривой второго порядка парабола A' g' i' i" g" A" x i"
- 29. Поверхности вращения с образующей кривой второго порядка гипербола i' A' g' g" A" i" i i
- 30. Винтовые поверхности Винтовая поверхность формируется при винтовом движении образующей (прямой или кривой) вокруг оси. Винтовое движение
- 32. Скачать презентацию





















 Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов)
Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов) Создание крышки редуктора
Создание крышки редуктора Виды аксонометрии
Виды аксонометрии Дисциплина начертательная геометрия
Дисциплина начертательная геометрия Деление окружности на 3, 4, 6 и 8 равных частей
Деление окружности на 3, 4, 6 и 8 равных частей Болтовое соединение
Болтовое соединение Проекционное черчение. Методы проецирования
Проекционное черчение. Методы проецирования Правила выполнения рабочей документации автоматизации технологических процессов
Правила выполнения рабочей документации автоматизации технологических процессов Особые случаи разрезов
Особые случаи разрезов Основные сведения по оформлению чертежей
Основные сведения по оформлению чертежей Аксонометрические проекции. Урок 1
Аксонометрические проекции. Урок 1 Индивидуальные задания по технологии. Тема: Проецирование
Индивидуальные задания по технологии. Тема: Проецирование Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании
Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании Технический рисунок
Технический рисунок Дисциплина:Современное проектирование зданий и сооружений. Основные параметры
Дисциплина:Современное проектирование зданий и сооружений. Основные параметры Архитектурно-строительное черчение
Архитектурно-строительное черчение Операционализация исследования
Операционализация исследования Порядок чтения чертежей деталей
Порядок чтения чертежей деталей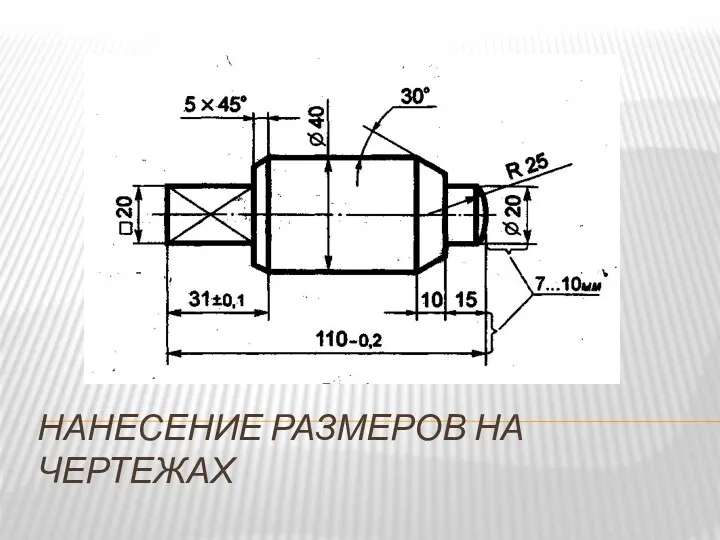 Нанесение размеров на чертежах
Нанесение размеров на чертежах Условности и упрощения на чертежах
Условности и упрощения на чертежах Сечения. Правила выполнения
Сечения. Правила выполнения Обозначение шероховатости поверхностей на чертежах
Обозначение шероховатости поверхностей на чертежах Архитектура. Построение плана здания
Архитектура. Построение плана здания Построение перспективы объекта методом архитекторов с недоступной точкой схода
Построение перспективы объекта методом архитекторов с недоступной точкой схода Сечения
Сечения Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей
Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей Аксонометрические проекции окружностей. 8 класс
Аксонометрические проекции окружностей. 8 класс Пересечение поверхностей вращения плоскостями
Пересечение поверхностей вращения плоскостями