Содержание
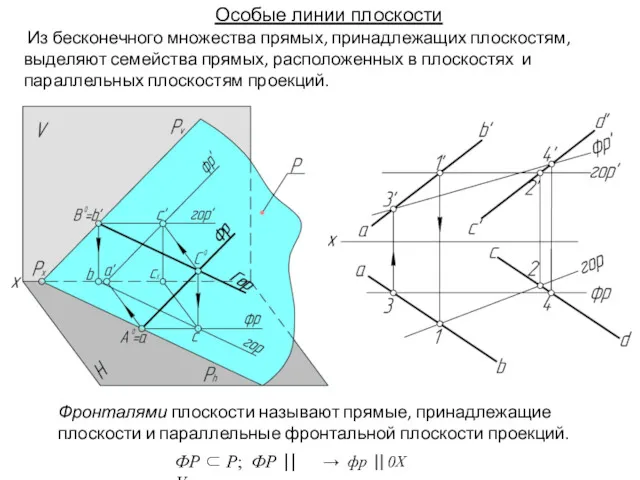
- 2. Особые линии плоскости Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства прямых, расположенных в плоскостях и
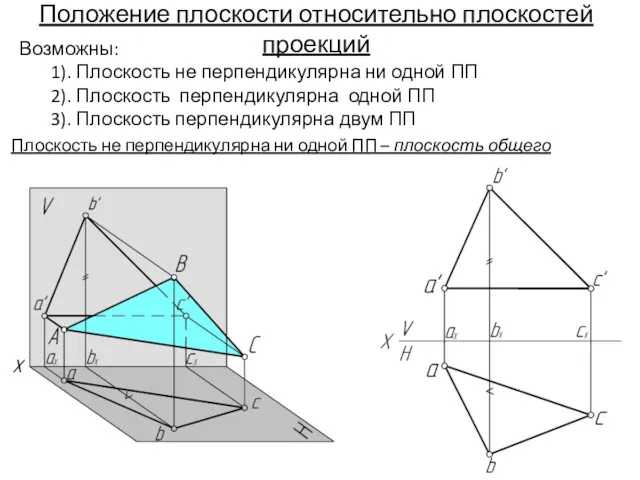
- 3. Положение плоскости относительно плоскостей проекций Возможны: 1). Плоскость не перпендикулярна ни одной ПП 2). Плоскость перпендикулярна
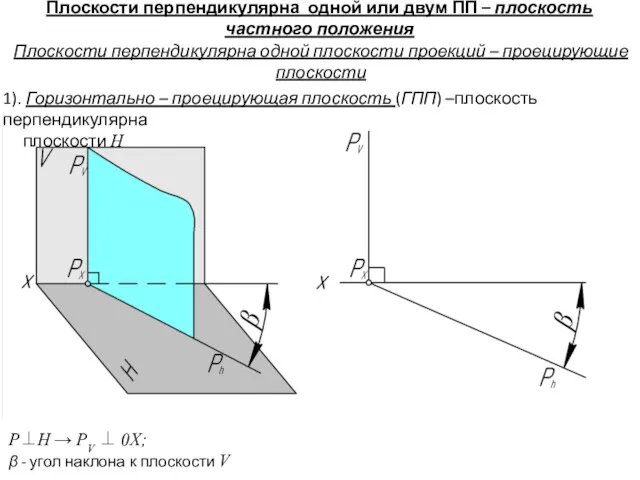
- 4. Плоскости перпендикулярна одной или двум ПП – плоскость частного положения Плоскости перпендикулярна одной плоскости проекций –
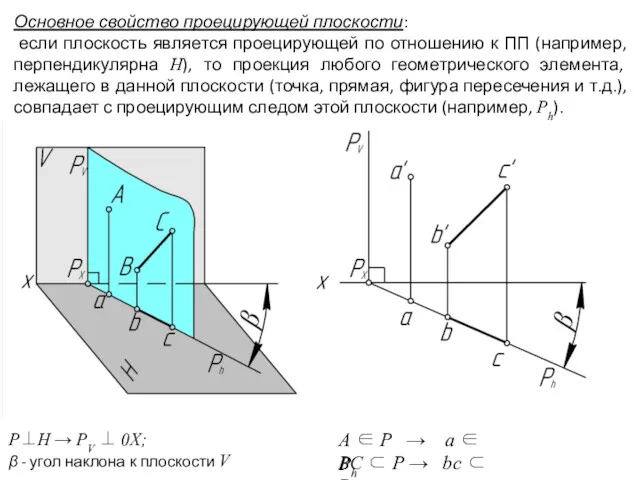
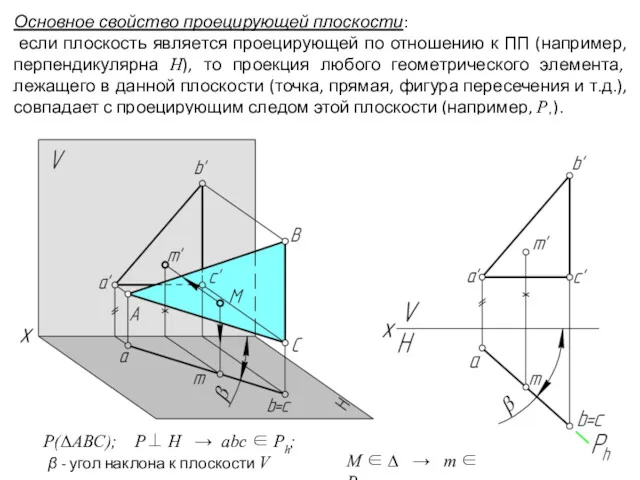
- 5. Основное свойство проецирующей плоскости: если плоскость является проецирующей по отношению к ПП (например, перпендикулярна Н), то
- 6. Основное свойство проецирующей плоскости: если плоскость является проецирующей по отношению к ПП (например, перпендикулярна Н), то
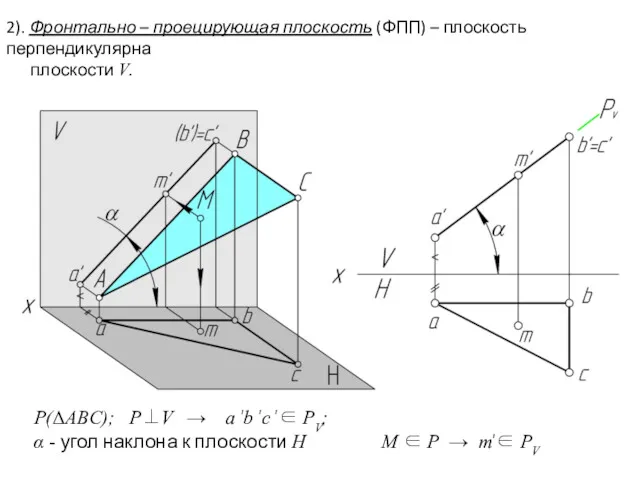
- 7. 2). Фронтально – проецирующая плоскость (ФПП) – плоскость перпендикулярна плоскости V. M ∈ P → m՛∈
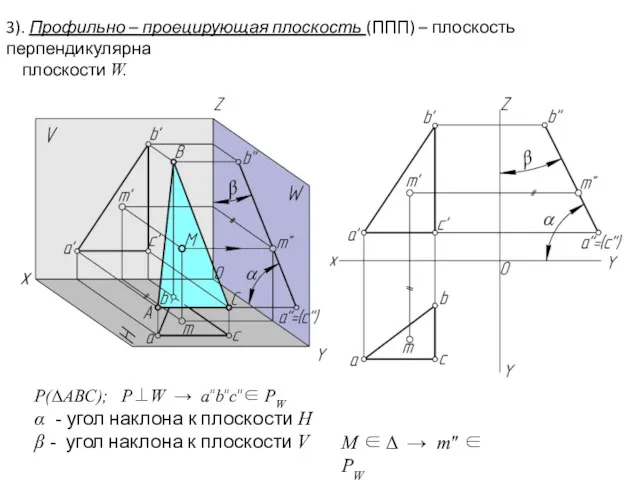
- 8. 3). Профильно – проецирующая плоскость (ППП) – плоскость перпендикулярна плоскости W. M ∈ Δ → m″
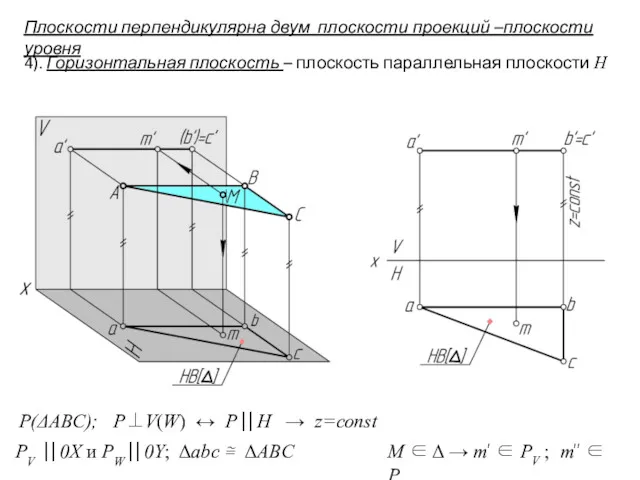
- 9. 4). Горизонтальная плоскость – плоскость параллельная плоскости Н P(ΔABC); P⊥V(W) ↔ P⎟⎟ H → z=const PV
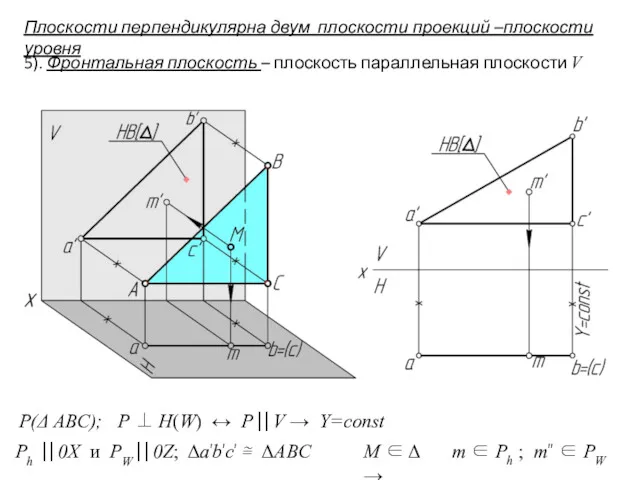
- 10. Плоскости перпендикулярна двум плоскости проекций –плоскости уровня 5). Фронтальная плоскость – плоскость параллельная плоскости V Ph
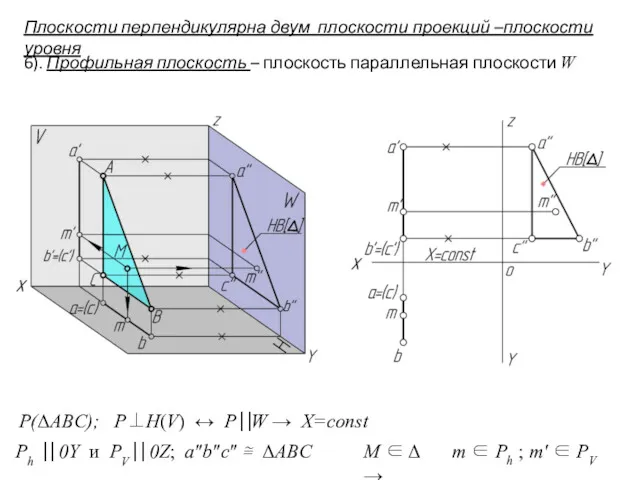
- 11. Плоскости перпендикулярна двум плоскости проекций –плоскости уровня 6). Профильная плоскость – плоскость параллельная плоскости W Ph
- 12. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ. ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ Пересечение прямой линии с проецирующей плоскостью Точка пересечения
- 13. Пересечение двух плоскостей, одна из которых проецирующая Дано: Параллелограмм (ABCD ) - общего положения Плоскость Р
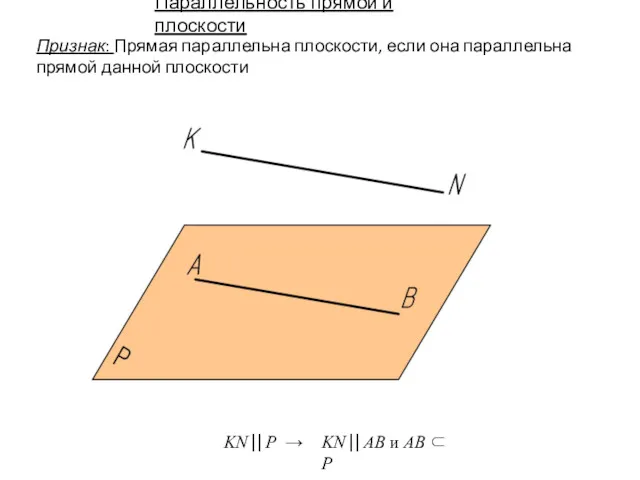
- 14. KN⎟⎟ P → KN⎟⎟ AB и AB ⊂ P Признак: Прямая параллельна плоскости, если она параллельна
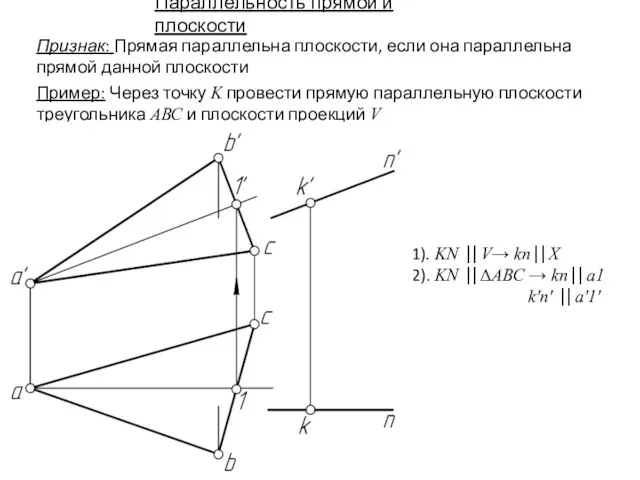
- 15. Параллельность прямой и плоскости 1). KN ⎟⎟ V→ kn⎟⎟ X 2). KN ⎟⎟ ΔABC → kn⎟⎟
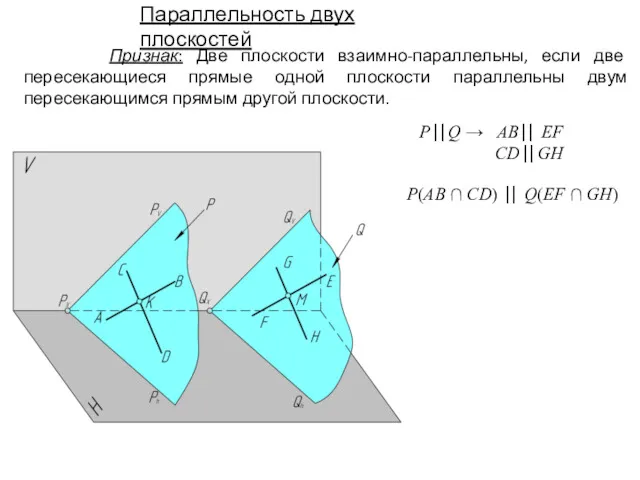
- 16. Признак: Две плоскости взаимно-параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.
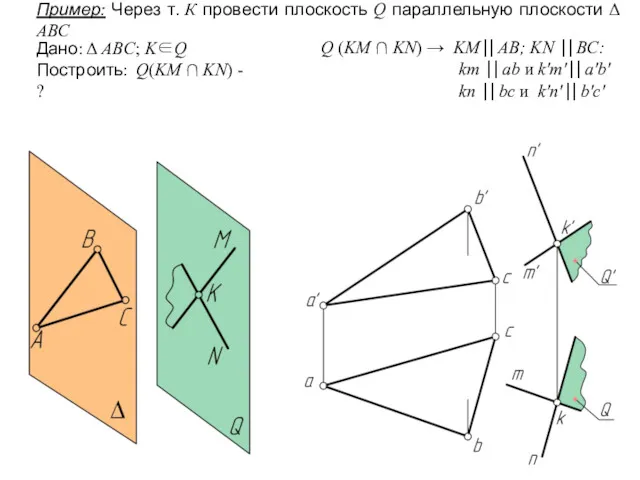
- 17. kn ⎟⎟ bc и k'n'⎟⎟ b'c' Q (KM ∩ KN) → KM⎟⎟ AB; KN ⎟⎟ BC:
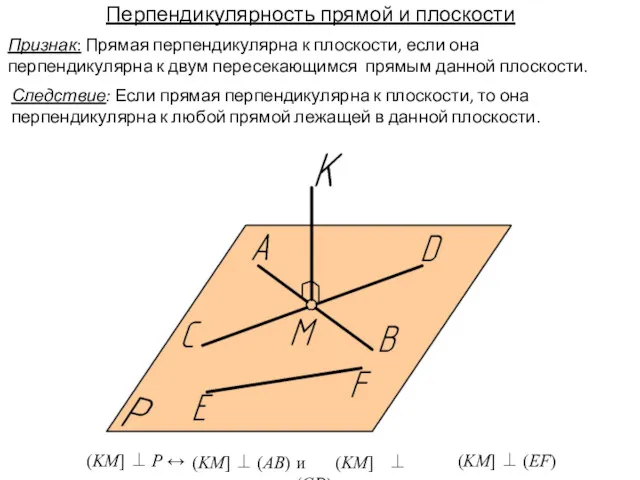
- 18. Следствие: Если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой лежащей в данной плоскости.
- 19. (KM] ⊥ P → km ⊥ гор k'm' ⊥ фр' Перпендикулярность прямой и плоскости Признак: Прямая
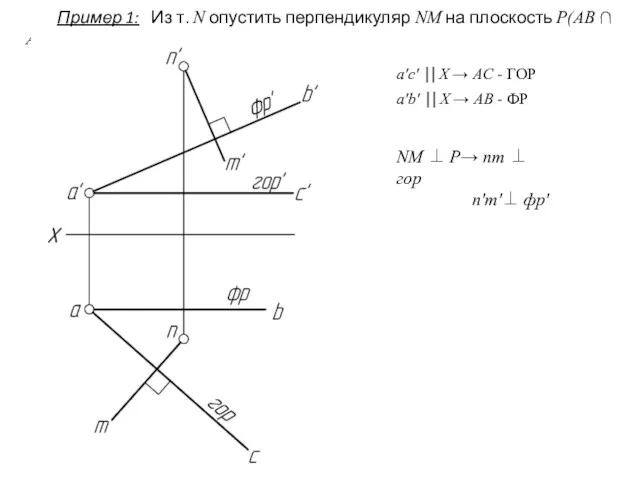
- 20. NM ⊥ P→ nm ⊥ гор n'm'⊥ фр' Пример 1: Из т. N опустить перпендикуляр NM
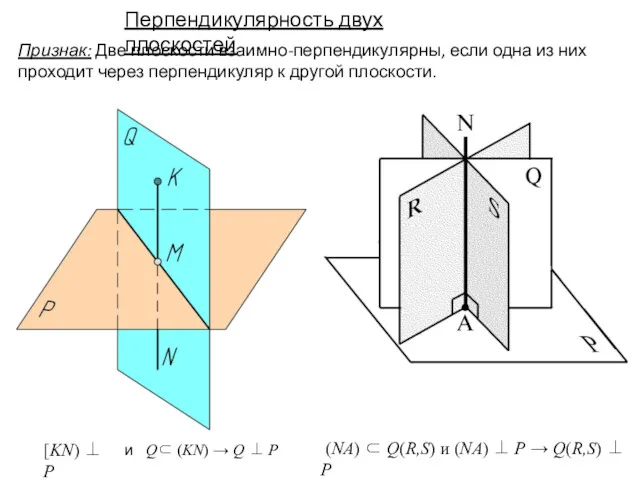
- 21. (NA) ⊂ Q(R,S) и (NA) ⊥ P → Q(R,S) ⊥ P [KN) ⊥ P Перпендикулярность двух
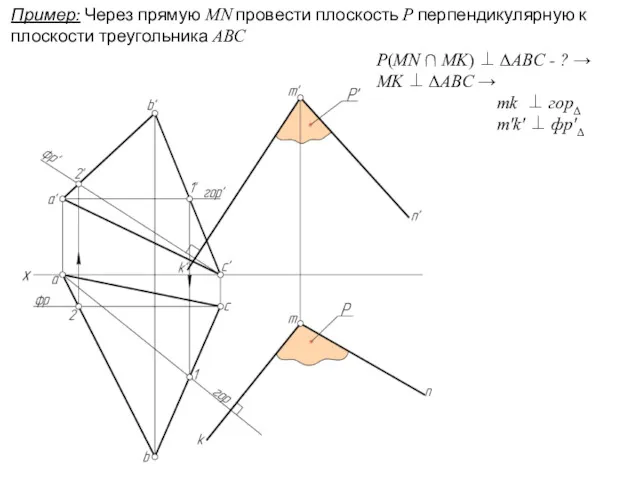
- 22. Пример: Через прямую MN провести плоскость Р перпендикулярную к плоскости треугольника ABC P(MN ∩ MK) ⊥
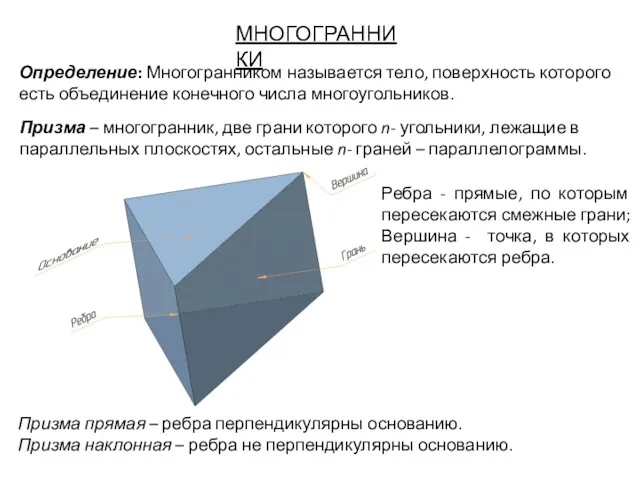
- 23. МНОГОГРАННИКИ Определение: Многогранником называется тело, поверхность которого есть объединение конечного числа многоугольников. Призма – многогранник, две
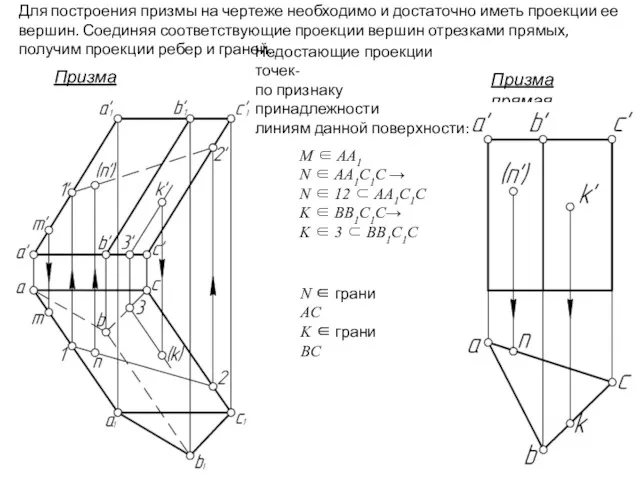
- 24. Для построения призмы на чертеже необходимо и достаточно иметь проекции ее вершин. Соединяя соответствующие проекции вершин
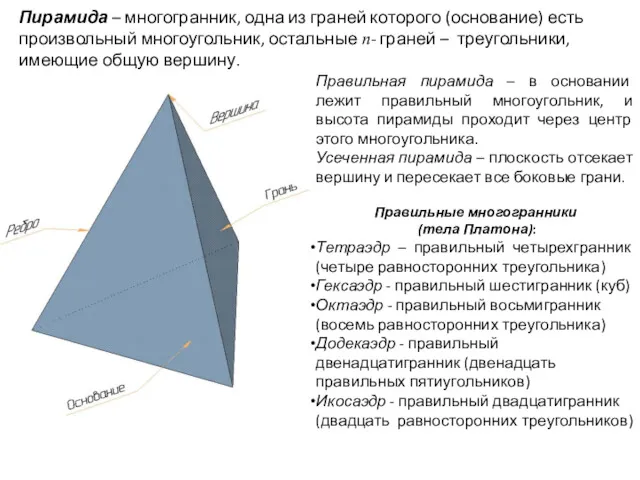
- 25. Правильная пирамида – в основании лежит правильный многоугольник, и высота пирамиды проходит через центр этого многоугольника.
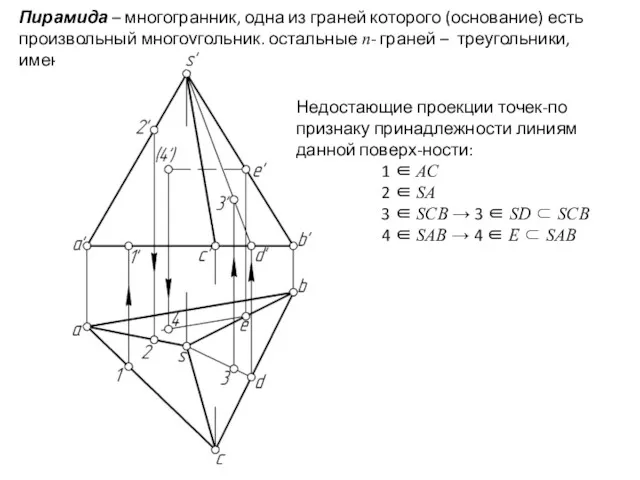
- 26. Пирамида – многогранник, одна из граней которого (основание) есть произвольный многоугольник, остальные n- граней – треугольники,
- 27. Пересечение многогранника проецирующей плоскостью. Натуральный вид фигуры сечения. Сечение многогранника – геометрическая фигура в результате пересечения
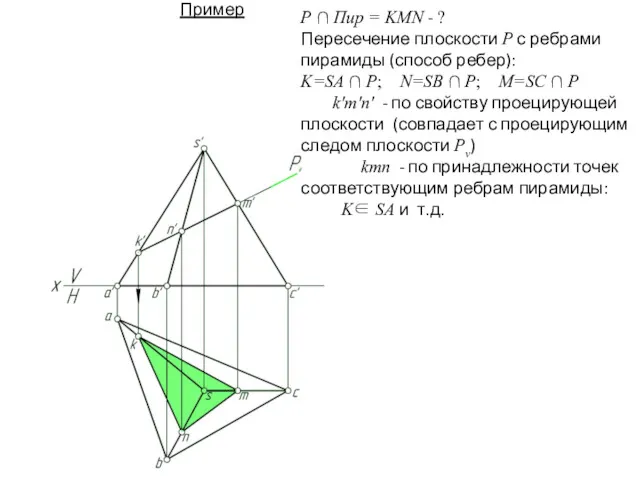
- 28. Пример 2: Р ∩ Пир = KMN - ? Пересечение плоскости Р с ребрами пирамиды (способ
- 30. Скачать презентацию


![(KM] ⊥ P → km ⊥ гор k'm' ⊥ фр'](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/118896/slide-18.jpg)

 Разрезы в аксонометрии. Алгоритм построения выреза в аксонометрической проекции
Разрезы в аксонометрии. Алгоритм построения выреза в аксонометрической проекции Задание точки, прямой, плоскости и многогранников на комплексном эпюре (чертеже) Монжа
Задание точки, прямой, плоскости и многогранников на комплексном эпюре (чертеже) Монжа Основные методы построения изображений
Основные методы построения изображений Изображение ландшафта средствами графики
Изображение ландшафта средствами графики Особенности ремонта и сборка резьбовых соединений
Особенности ремонта и сборка резьбовых соединений Проецирование геометрических тел
Проецирование геометрических тел Аксонометричні проекції. Послідовність виконання
Аксонометричні проекції. Послідовність виконання Построение теней архитектурного сооружения. Практическое занятие №3
Построение теней архитектурного сооружения. Практическое занятие №3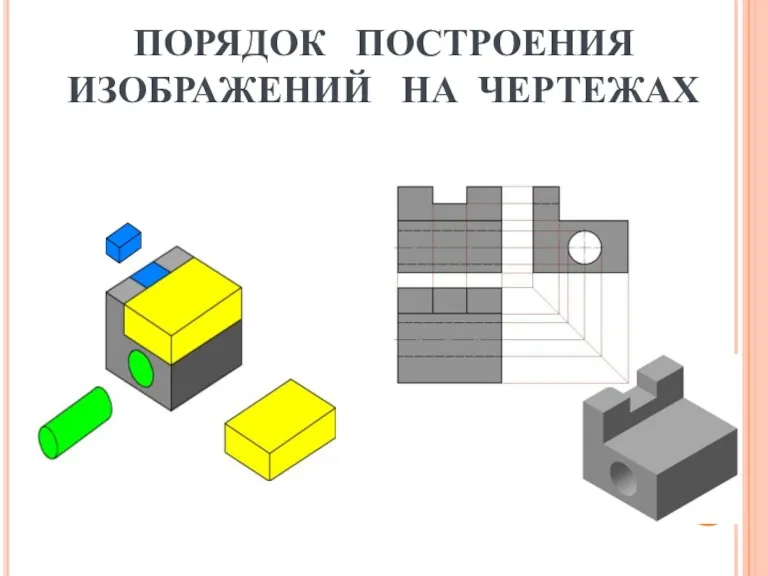 Порядок построения изображений на чертежах
Порядок построения изображений на чертежах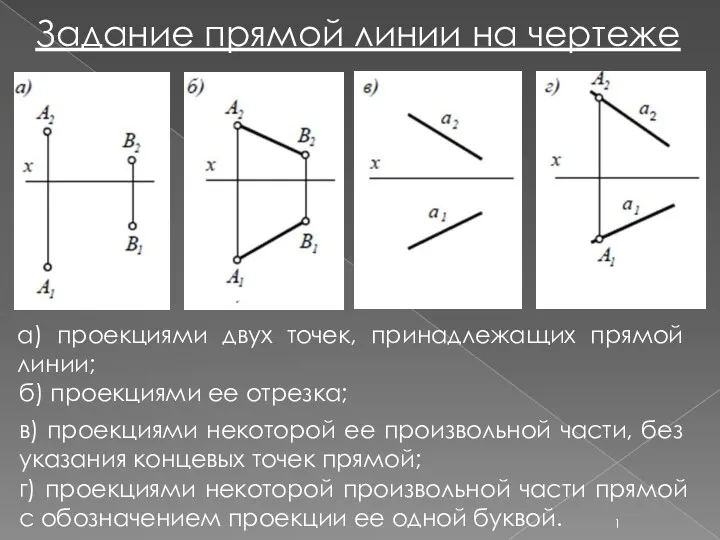 Задание прямой линии на чертеже
Задание прямой линии на чертеже Разрез здания. Лестница
Разрез здания. Лестница Виды соединений. Сборочные чертежи
Виды соединений. Сборочные чертежи Задание плоскости на чертеже. Взаимное положение прямой и плоскости, двух плоскостей. Проекции многогранников. Лекция 2
Задание плоскости на чертеже. Взаимное положение прямой и плоскости, двух плоскостей. Проекции многогранников. Лекция 2 Поверхности. Задание поверхности на чертеже
Поверхности. Задание поверхности на чертеже Нивелирование. Способы нивелирования
Нивелирование. Способы нивелирования Общие правила оформления чертежей
Общие правила оформления чертежей Проектування технологічного процесу виготовлення виливка Корпус з фланцем з мідного сплаву
Проектування технологічного процесу виготовлення виливка Корпус з фланцем з мідного сплаву Перспектива. Метод архитекторов
Перспектива. Метод архитекторов Рекомендации по выполнению контрольной работы по инженерной графике
Рекомендации по выполнению контрольной работы по инженерной графике Основные параметры шероховатости поверхности
Основные параметры шероховатости поверхности Разрез предмета
Разрез предмета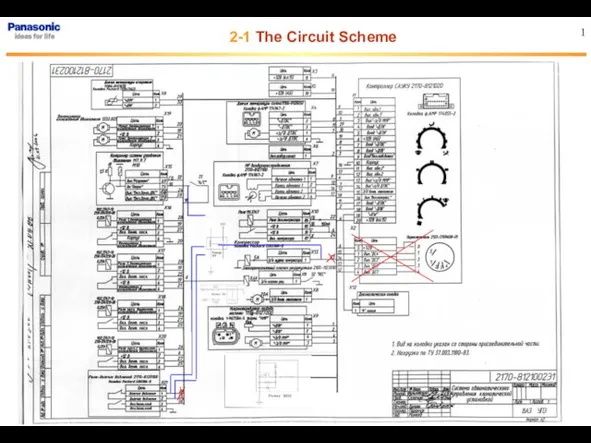 Схема климатической установки Панасоник
Схема климатической установки Панасоник Тени в ортогональных проекциях
Тени в ортогональных проекциях Пересечение многогранников
Пересечение многогранников Разработка и реализация технологического процесса изготовления детали, вал-шестерня z=15 m=2
Разработка и реализация технологического процесса изготовления детали, вал-шестерня z=15 m=2 Резьба. Классификация резьбы. Изображение и обозначение резьбы на чертежах
Резьба. Классификация резьбы. Изображение и обозначение резьбы на чертежах Аксонометрические проекции
Аксонометрические проекции Чертеж - конструкторский документ
Чертеж - конструкторский документ