Содержание
- 2. - оператор кинетической энергии электронов - оператор кинетической энергии ядер - энергия электрон-электронного взаимодействия - энергия
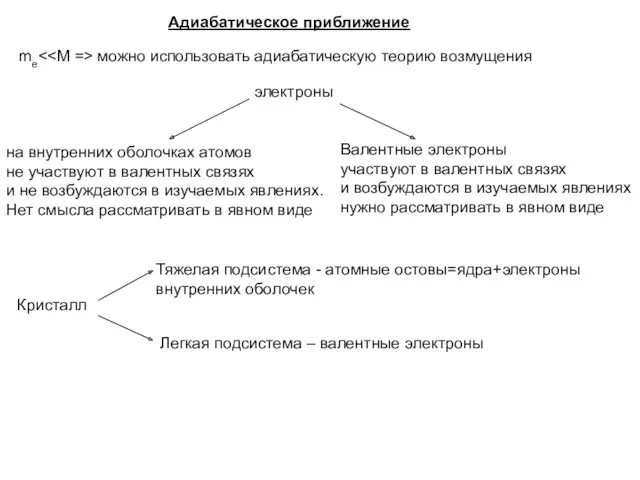
- 3. me можно использовать адиабатическую теорию возмущения Адиабатическое приближение электроны на внутренних оболочках атомов не участвуют в
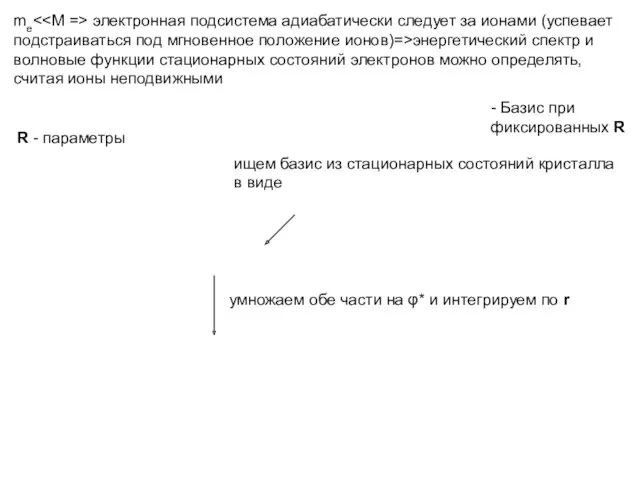
- 4. me электронная подсистема адиабатически следует за ионами (успевает подстраиваться под мгновенное положение ионов)=>энергетический спектр и волновые
- 5. - приводит к неадиабат. поправкам порядка (m/M)1/4 Пренебрегаем неадиабатическими поправками - СУШ для ионов во внешнем
- 6. Приближение самосогласованного поля Хартри-Фока для электронной подсистемы кристалла
- 7. Надо Найти стационарные состояния электронной подсистемы в поле V(r) неподвижных ядер Проблема та же – из-за
- 8. Приближение самосогласованного поля Хартри-Фока Базовое предположение: Это приближение состоит в предположении, что каждый электрон, “чувствует” некоторое
- 9. - Одноэлектронный Гамильтониан (Гамильтониан одного отдельно взятого электрона в тех же силовых полях, что и весь
- 11. Как определить самосогласованное поле Ueff? Простейший вариант – как электростатическое поле, создаваемое средней электронной плотностью Поле
- 12. Выражение для волновой функции можно определить из вариационного принципа квантовой механики Наилучшее приближение для волновой функции
- 13. Зонная теория для идеального кристалла в отсутствие внешних полей. Задача Блоха
- 14. Надо: одноэлектронные стационарные состояния для случая, когда все атомы находятся в положении равновесия (хорошая нулевая задача)
- 15. , если уровень Е - невырожденный Что будет если уровень энергии Е является вырожденным? Е вырожден
- 16. Известна линейно независимая система решений Выбор такой системы решений – неоднозначный Нужно подобрать такие коэффициенты в
- 17. - задача диагонализации матрицы - ОСЛАУ
- 18. Вектор k определяет закон, связывающий значения волновой функции электрона в точках, отстоящих друг от друга на
- 19. Можно сформировать базис из волновых функций стационарных состояний, каждая из которых удовлетворяет условию Обратная решетка Def.
- 20. - объем элементарной ячейки
- 21. только если Периодическая функция с периодом кристаллической (прямой) решетки
- 22. Th Блоха (Bloch). волновая функция стационарного состояния электрона в периодическом поле Волновая функция Блоха известна, если
- 23. Уравнение для периодической части функции Блоха - известна, если известна u Уравнение Шредингера для u
- 24. Уравнение для периодической части функции Блоха
- 25. Уравнение для периодической части функции Блоха
- 26. Уравнение для периодической части функции Блоха Уравнение Шредингера для электрона в идеальном кристалле, позволяющее найти энергию
- 27. Th Блоха (Bloch). волновая функция стационарного состояния электрона в периодическом поле Cтационарное состояние электрона в периодическом
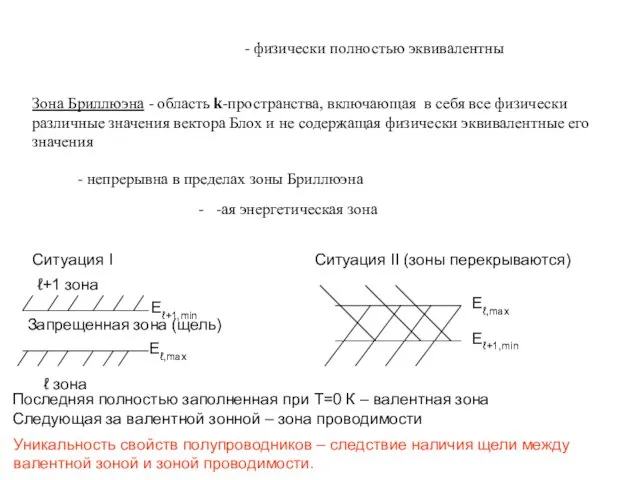
- 28. - физически полностью эквивалентны Зона Бриллюэна - область k-пространства, включающая в себя все физически различные значения
- 29. Эффективная масса: невырожденный экстремум - тензор обратных эффективных масс -скалярная эффективная масса вдоль оси α
- 30. Эффективная масса: невырожденный экстремум Закон дисперсии вдоль главной оси имеет такой же вид, как и для
- 31. Эффективная масса: невырожденный экстремум Во многих физических процессов большая часть носителей заряда находится в окрестности экстремумов
- 32. Эффективная масса: невырожденный экстремум Гравитационная масса электрона (его масса покоя) является фундаментальной физической константой, тогда как
- 33. kp-метод: основная идея метод, позволяющий вычислить состояния Блоха в окрестности экстремума зоны - Гамильтониан для k=0
- 34. Невыожденный экстремум => энергия ν-ой зоны – невырожденная в точке экстремума (такую энергию имеет только одно
- 35. kp-метод: невырожденный экстремум Периодические части блоховских функция с одинаковым kобразуют ортонормированный набор - матричный элемент проекции
- 36. kp-метод: невырожденный экстремум Поправка первого порядка малости ν=μ Происходит сдвиг точки экстремума
- 37. kp-метод: невырожденный экстремум Поправка второго порядка малости μ ≠ ν
- 38. kp-метод: невырожденный экстремум Эффективная масса определяется матичным элементом оператора импульса в экстремуме
- 39. Используется стационарная теория возмущения при наличии вырождения kp-метод: вырожденный экстремум
- 40. F(r) – периодическая функция с периодом кристаллической решетки Def. G вектор обратной решетки ⬄ только если
- 41. Th. Если F(r)=F(r+n), тогда разложение Фурье F(r) содержит только плоские волны с волновыми векторами, совпадающими с
- 42. Решеточные суммы
- 43. Решеточные суммы
- 45. Скачать презентацию







































 Гидромеханика. Основные понятия и определения
Гидромеханика. Основные понятия и определения Интерференция света. Условие интерференции
Интерференция света. Условие интерференции Феромагнетики. Феромагнітне тіло
Феромагнетики. Феромагнітне тіло Правка, разметка и резание тонколистового металла
Правка, разметка и резание тонколистового металла Международная система единиц СИ
Международная система единиц СИ Introducing. Mate Precision Tooling
Introducing. Mate Precision Tooling Постоянные магниты. Магнитное поле Земли
Постоянные магниты. Магнитное поле Земли Характеристики спектров кристаллов
Характеристики спектров кристаллов Технология Критического мышления на уроках физики .
Технология Критического мышления на уроках физики . Восстановление деталей синтетическими материалами
Восстановление деталей синтетическими материалами Физика ЕГЭ. Задание 14
Физика ЕГЭ. Задание 14 Состав и схемы автоматических систем
Состав и схемы автоматических систем Импульс тела презентация к уроку физики
Импульс тела презентация к уроку физики Камера Вильсона
Камера Вильсона Электрический ток в вакууме
Электрический ток в вакууме Применение ПКМ при ремонте машин
Применение ПКМ при ремонте машин Проектирование и расчет металлоконструкций грузоподъемных машин.Лекция №6
Проектирование и расчет металлоконструкций грузоподъемных машин.Лекция №6 Основы атомной физики. Основы квантовой механики. Строение вещества
Основы атомной физики. Основы квантовой механики. Строение вещества Открытый урок по физике в 9 классе Реактивное движение
Открытый урок по физике в 9 классе Реактивное движение Механическое движение. Что называют механическим движением?
Механическое движение. Что называют механическим движением? Презентация по физике Световые явления для 8 класса
Презентация по физике Световые явления для 8 класса Автосцепное устройство железнодорожного подвижного состава. Лекция №6
Автосцепное устройство железнодорожного подвижного состава. Лекция №6 Турбулентные течения
Турбулентные течения Электрический заряд и его свойства. Закон Кулона
Электрический заряд и его свойства. Закон Кулона Решение задач по теме давление в жидкостях
Решение задач по теме давление в жидкостях Особенности заданий ЕГЭ. Колебания и волны
Особенности заданий ЕГЭ. Колебания и волны Устройство и принцип работы воздухораспределителя 292
Устройство и принцип работы воздухораспределителя 292 Ускорители заряженных частиц. Магнитное поле
Ускорители заряженных частиц. Магнитное поле