Динамика механической системы и твердого тела(§9 - §11). Теорема об изменении момента количества движения системы презентация
Содержание
- 2. § 9. Теорема об изменении момента количества движения системы Главным моментом количества движения, или кинетическим моментом
- 3. Рассмотрим главный момент количества движения вращающегося тела с угловой скоростью ω Линейная скорость точки К: hK
- 4. Если система состоит из нескольких тел, вращающихся вокруг одной оси Z, то кинетический момент системы будет
- 5. Докажем эти выражения. Проекции скорости на оси Х и Y тогда
- 6. Но если ось OZ будет главной осью инерции тела (осью симметрии тела), то не направлен по
- 7. Составляя такие уравнения для всех точек системы и складывая почленно, получим Тогда по свойству внутренних сил
- 8. Проектируем обе части равенства (5) на неподвижные оси Оxyz, получим Уравнения (6) выражают теорему моментов относительно
- 9. Cx’y’z’ – оси, перемещающиеся поступательно вместе с центром масс системы С с ускорением 9.1. Плоско-параллельное движение
- 10. Просуммируем по всем точкам тела уравнения (7) и (8) Относительно точки С необходимо добавить переносную силу
- 11. причем здесь V’k – скорости точек системы по отношению к подвижным осям СX’Y’Z’, т.к. оси движутся
- 12. В результате (9) Для системы, движущейся свободно или плоско-параллельно, т.е. подвижная система отсчета совершает поступательное движение
- 13. тогда главный момент количеств движения системы относительно этого же центра будет численно и по направлению постоянен
- 14. Внутренние силы изменить главный момент количеств движения механической системы не могут!!! Рассмотрим систему, вращающуюся вокруг неподвижной
- 15. , => a) если система не изменяема (абсолютно твердое тело), то Т.к. и б) если система
- 16. § 10. Теорема об изменении кинетической энергии системы Кинетической энергией системы (Т) называется скалярная величина, равная
- 17. При поступательном движении кинетическая энергия системы равна половине массы системы, умноженной на квадрат скорости её центра
- 18. 10.2. Вращательное движение системы Если тело вращается вокруг какой-либо оси OZ, то скорость любой его точки
- 19. 10.3. Плоско-параллельное движение системы Скорости всех точек системы в каждый момент времени распределены так, как если
- 20. Введем постоянный момент инерции JC относительно центра масс - скорость центра масс но Кинетическая энергия системы,
- 21. Просуммируем по всем точкам системы Теорема об изменении кинетической энергии системы в дифференциальной форме Пусть механическая
- 22. Проинтегрируем уравнение (14) или Изменение кинетической энергии системы при некотором её перемещении равно сумме работ на
- 23. Работа сил тяжести, действующих на систему, есть работа их главного вектора Р на перемещении центра масс
- 24. 11.2. Работа сил, приложенных к вращающемуся телу Пусть тело вращается вокруг какой-либо оси OZ c угловой
- 25. В случае постоянного вращающего момента (18) Тогда (17) При повороте на конечный угол (19)
- 26. 11.3. Работа сил трения, действующих на катящееся тело а) качение без скольжения по твердой поверхности Т.к.
- 28. Скачать презентацию

























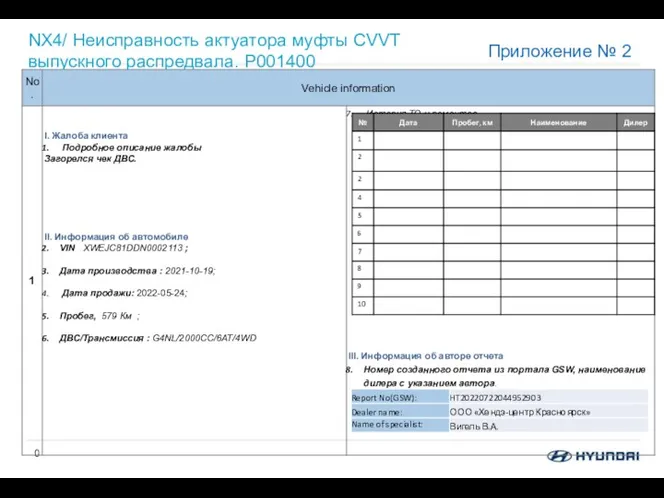 Неисправность актуатора муфты CVVT выпускного распредвала. P001400
Неисправность актуатора муфты CVVT выпускного распредвала. P001400 Wings. Types of Aircraft Wings
Wings. Types of Aircraft Wings Определение зависимости силы трения скольжения от веса тела
Определение зависимости силы трения скольжения от веса тела Школа кота Леопольда
Школа кота Леопольда Зачем физика повару?
Зачем физика повару? Двигатель Cummins ISF 2.8
Двигатель Cummins ISF 2.8 Механізація подрібнення стеблових кормів
Механізація подрібнення стеблових кормів Линза. Построение изображений, даваемых линзой
Линза. Построение изображений, даваемых линзой Динаміка матеріальної точки
Динаміка матеріальної точки Закон Паскаля. Сполучені посудини
Закон Паскаля. Сполучені посудини Магнитные цепи
Магнитные цепи Законы сохранения в механике
Законы сохранения в механике Применение аккумуляторов
Применение аккумуляторов Найзағайдың түрлері
Найзағайдың түрлері Теория судна. Статика. Лекция № 1. Геометрия корпуса судна
Теория судна. Статика. Лекция № 1. Геометрия корпуса судна Наблюдение сплошного и линейчатых спектров
Наблюдение сплошного и линейчатых спектров Нагревание проводников электрическим током. Закон Джоуля – Ленца
Нагревание проводников электрическим током. Закон Джоуля – Ленца Точечные дефекты и их влияние на свойства кристаллов. Равновесные и неравновесные дефекты. Примеси в полупроводниках
Точечные дефекты и их влияние на свойства кристаллов. Равновесные и неравновесные дефекты. Примеси в полупроводниках Дифракционная решетка
Дифракционная решетка Физика вокруг нас
Физика вокруг нас Свтовые кванты
Свтовые кванты Презентация к уроку Свет и цвет
Презентация к уроку Свет и цвет квантовая физика
квантовая физика Переходные процессы
Переходные процессы Количество теплоты. Единицы количества теплоты. Удельная теплоемкость
Количество теплоты. Единицы количества теплоты. Удельная теплоемкость Движение тела под действием силы тяжести
Движение тела под действием силы тяжести Урок по физике в 8 классе на тему Влажность воздуха
Урок по физике в 8 классе на тему Влажность воздуха Молекулярная физика
Молекулярная физика