Содержание
- 2. Вопросы: Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Электроемкость проводников и конденса-торов. (Емкости плоского,
- 3. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Поместим металлический проводник во внешнее электростатическое поле
- 4. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Избыточные заряды появляются лишь на поверхности проводника
- 5. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Второе условие равновесия зарядов на проводнике: в
- 6. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Таким образом, если в полости проводника нет
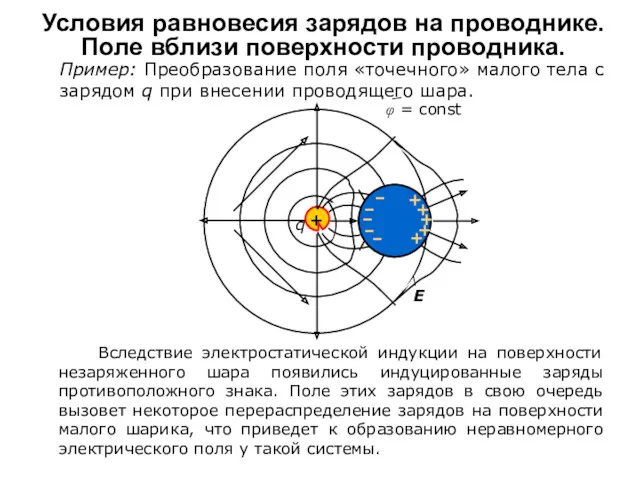
- 7. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Пример: Преобразование поля «точечного» малого тела с
- 8. Условия равновесия зарядов на проводнике. Поле вблизи поверхности проводника. Расчет поля у поверхности проводника. Пусть интересующий
- 9. Электроемкость проводников и конденсаторов Емкость проводников Рассмотрим некоторый уединенный проводник, т. е. проводник, удаленный от других
- 10. Электроемкость проводников и конденсаторов Следовательно отношение не зависит от заряда и для каждого уединенного проводника имеет
- 11. Электроемкость проводников и конденсаторов Емкость конденсаторов Уединенные проводники, вообще говоря, обладают небольшой емкостью. На практике же
- 12. Электроемкость проводников и конденсаторов Таким образом, потенциал проводника, как алгебраи-ческая сумма (4), уменьшается при приближении к
- 13. Электроемкость проводников и конденсаторов Емкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его
- 14. Электроемкость проводников и конденсаторов Пример 2: Емкость цилиндрического конденсатора. Заданы: размеры конденсатора (R1 , R2 ,
- 15. Электроемкость проводников и конденсаторов Пример 3: Емкость сферического конденсатора. Заданы: размеры конденсатора (R1, R2), проницаемость однородного
- 16. Энергия системы неподвижных зарядов Энергия взаимодействия системы зарядов Ранее было получено выражение для потенциальной энергии взаимодействия
- 17. Энергия системы неподвижных зарядов Полная энергия взаимодействия системы непрерывно распределенных зарядов Если заряды распределены непрерывно (допустим,
- 18. Энергия заряженного проводника и конденсатора Энергия уединенного заряженного проводника Пусть проводник имеет заряд q и потенциал
- 19. Энергия заряженного проводника и конденсатора Энергия конденсатора Пусть +q и φ1 – заряд и потенциал положительно
- 20. Плотность энергии электростатического поля О локализации энергии электрического поля Формула (7) определяет энергию любой электричес-кой системы
- 21. Плотность энергии электростатического поля Так как электрическое поле в плоском конденсаторе однородно, то заключенная в нем
- 23. Скачать презентацию



















 Адиабатическое приближение в твердом теле
Адиабатическое приближение в твердом теле Стабилитроны
Стабилитроны Формы и методы подготовки учащихся к ГИА по физике
Формы и методы подготовки учащихся к ГИА по физике Топ-5 перспективных разработок атомной энергетики
Топ-5 перспективных разработок атомной энергетики ВКР: Получение нанодисперсной магнитной жидкости на полярной основе методом химической конденсации
ВКР: Получение нанодисперсной магнитной жидкости на полярной основе методом химической конденсации Преимущества и недостатки использования оптических волокон в системах связи
Преимущества и недостатки использования оптических волокон в системах связи Импульсные сигналы и переходные процессы. Общие сведения об импульсных сигналах
Импульсные сигналы и переходные процессы. Общие сведения об импульсных сигналах Конвективный теплообмен. (Лекция 10)
Конвективный теплообмен. (Лекция 10) Стандартная модель. Космогония современного мира
Стандартная модель. Космогония современного мира Устройство автомобиля – шасси. Подвеска автомобиля
Устройство автомобиля – шасси. Подвеска автомобиля Как называются частицы, из которых состоят вещества?
Как называются частицы, из которых состоят вещества? 10 класс. Презентация по физике на тему Конденсаторы
10 класс. Презентация по физике на тему Конденсаторы Магнитооптические материалы
Магнитооптические материалы Свойства уравнений Максвелла
Свойства уравнений Максвелла Физика. Молекулярно-кинетическая теория
Физика. Молекулярно-кинетическая теория Статистические и термодинамические свойства макросистем
Статистические и термодинамические свойства макросистем Обертальний рух в природі
Обертальний рух в природі Урок в 8 классе Сила тока.
Урок в 8 классе Сила тока. Внеклассное мероприятие Конкурс изобретателей
Внеклассное мероприятие Конкурс изобретателей использование интерактивного обордования на роках физики
использование интерактивного обордования на роках физики Исследование особенностей проектирования и анализа плавучего отеля с катамаранным корпусом
Исследование особенностей проектирования и анализа плавучего отеля с катамаранным корпусом Теоретические основы электротехники. Основные законы электрических цепей
Теоретические основы электротехники. Основные законы электрических цепей Устройство и безопасная эксплуатация строительных подъемников
Устройство и безопасная эксплуатация строительных подъемников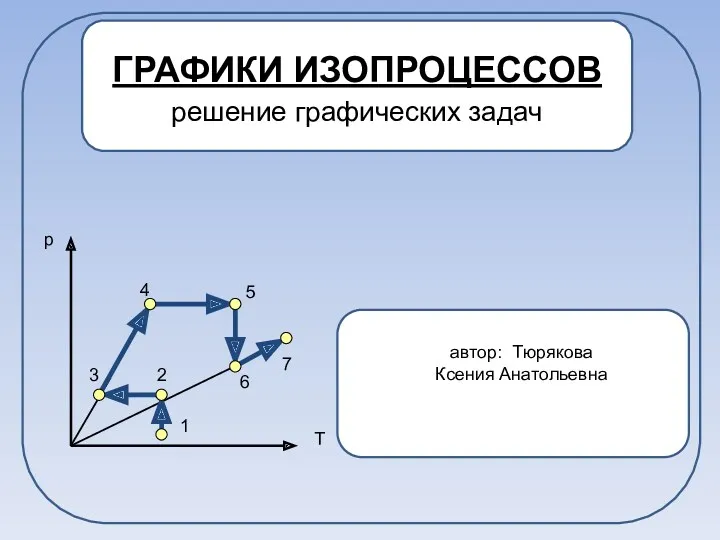 Графики изопроцессов. Решение графических задач
Графики изопроцессов. Решение графических задач Инжекторная система впрыска топлива
Инжекторная система впрыска топлива Зубчатые передачи
Зубчатые передачи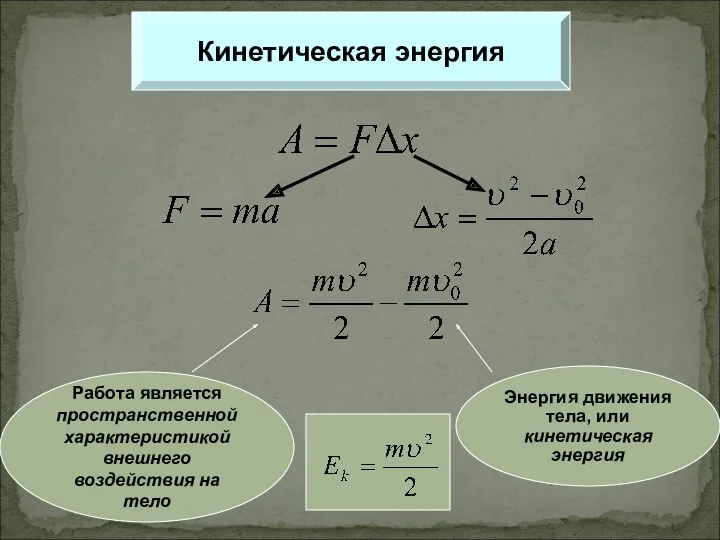 Кинетическая энергия
Кинетическая энергия Электрический ток в газах
Электрический ток в газах