Содержание
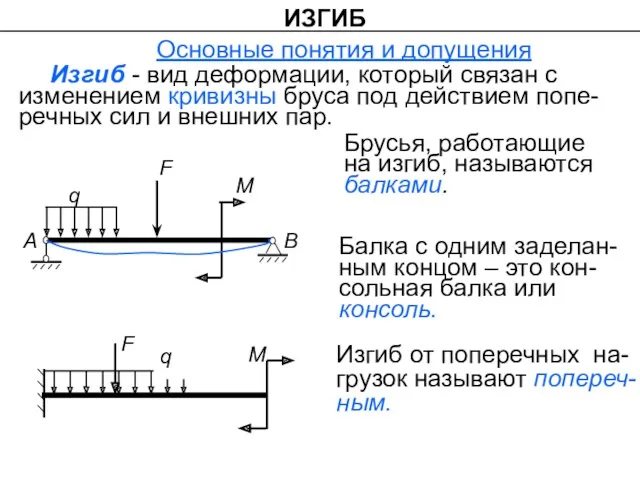
- 2. Основные понятия и допущения Изгиб - вид деформации, который связан с изменением кривизны бруса под действием
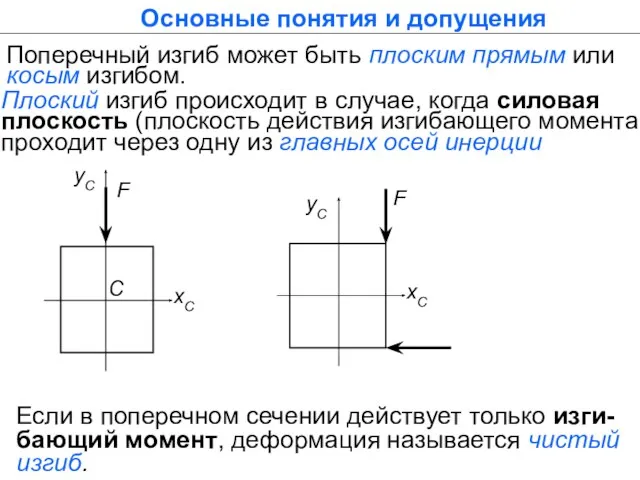
- 3. Поперечный изгиб может быть плоским прямым или косым изгибом. Плоский изгиб происходит в случае, когда силовая
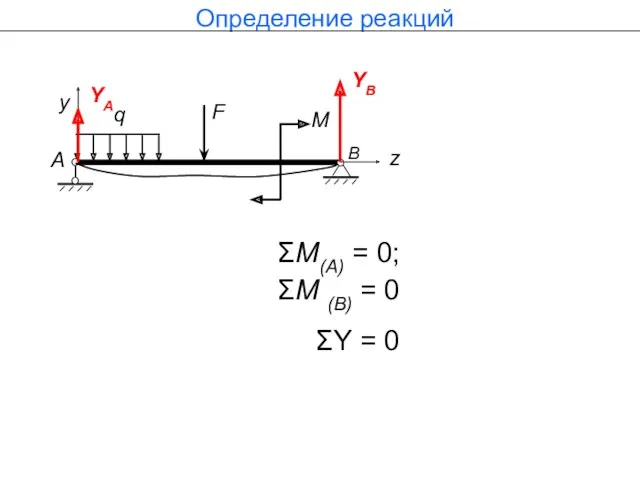
- 4. Определение реакций 2. шарнирно-подвижная опора (стержень с шарнирами на концах) При изгибе для закрепления балки, в
- 5. Определение реакций Так как все силы действуют перпендикулярно про- дольной оси балки, горизонтальная составляющая реакции равна
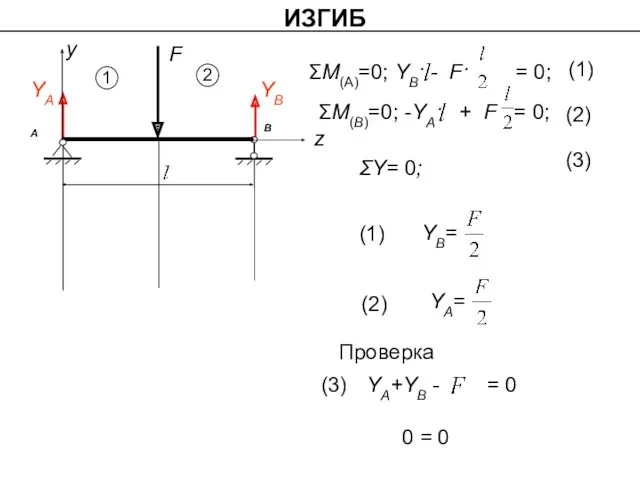
- 6. ΣМ(А) = 0; ΣМ (В) = 0 Определение реакций YA YB ΣY = 0
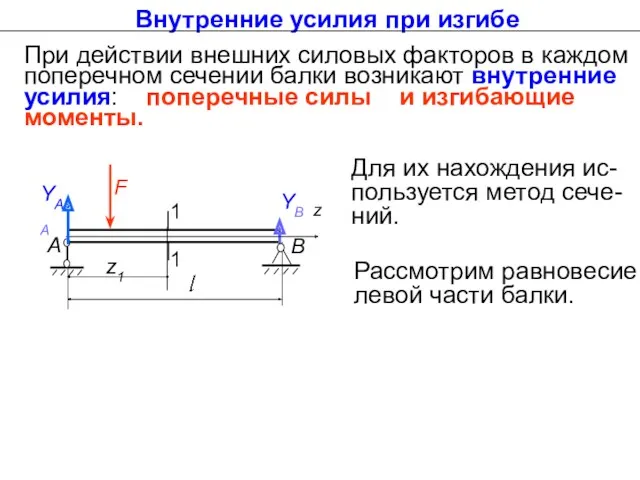
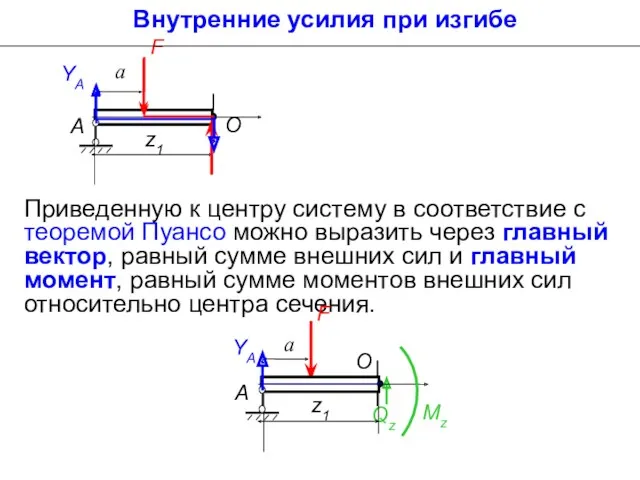
- 7. Внутренние усилия при изгибе При действии внешних силовых факторов в каждом поперечном сечении балки возникают внутренние
- 8. Выполним приведение системы сил к центру сечения О. В соответствие с леммой Пуансо, силу, действую-щую на
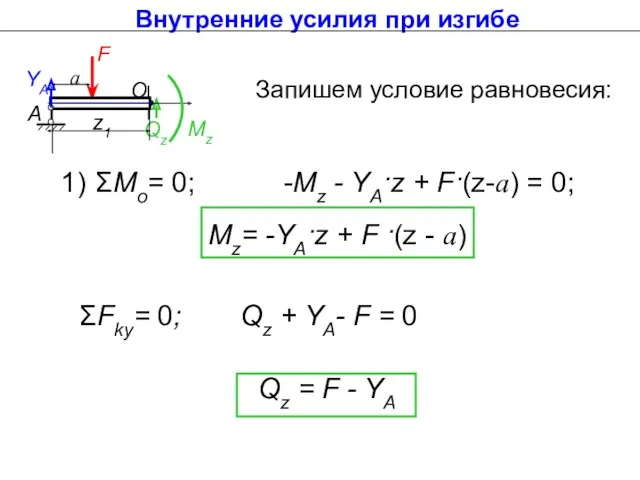
- 9. Внутренние усилия при изгибе Приведенную к центру систему в соответствие с теоремой Пуансо можно выразить через
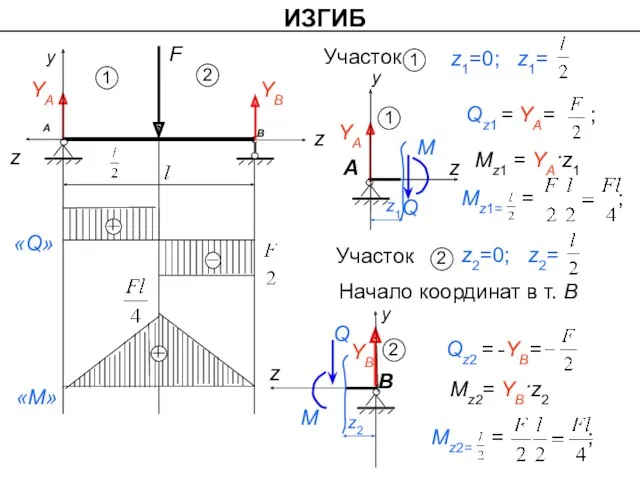
- 10. Запишем условие равновесия: ΣFky= 0; Qz O Mz А F YA z1 a Внутренние усилия при
- 11. Внутренние усилия при изгибе Изгибающий момент Мz в любом сечении равен алгебраической сумме моментов всех сил,
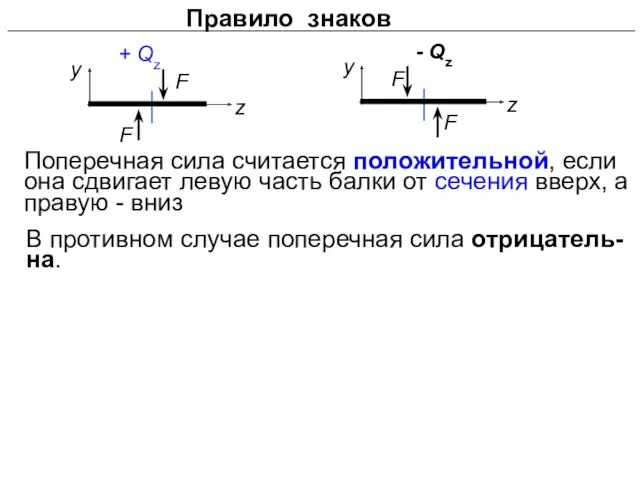
- 12. Правило знаков Поперечная сила считается положительной, если она сдвигает левую часть балки от сечения вверх, а
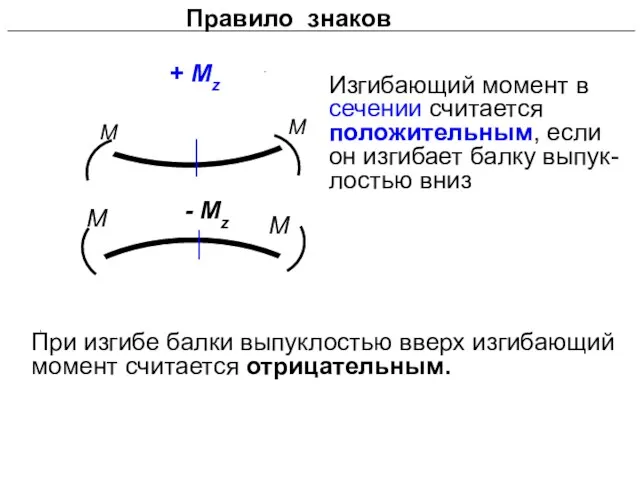
- 13. M M - Mz M M Изгибающий момент в сечении считается положительным, если он изгибает балку
- 14. Порядок построения эпюр 6. Строят в принятом масштабе эпюры Qz и Мz, откладывая вверх от оси
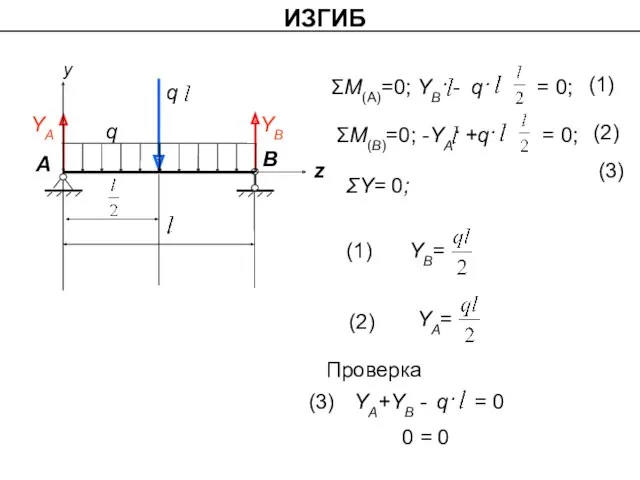
- 15. ИЗГИБ q YA YB ΣY= 0; (1) (2) (3) (1) (2) (3) 0 = 0 Проверка
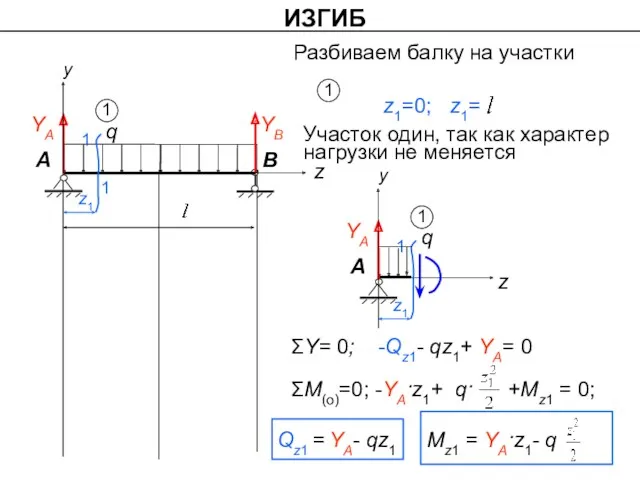
- 16. ИЗГИБ y q A B z YA YB z1 1 1 Разбиваем балку на участки z1=0;
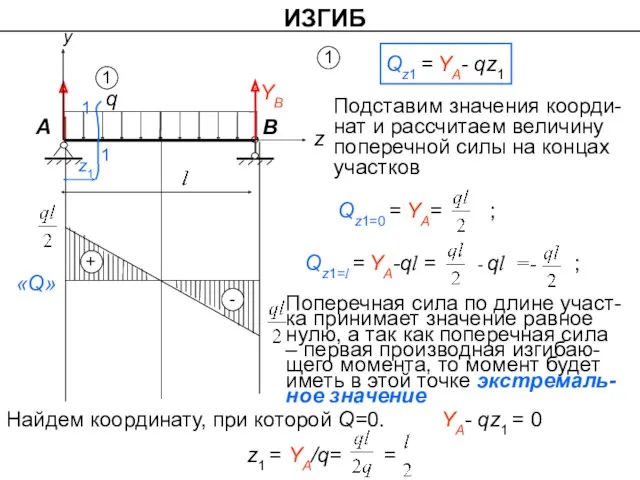
- 17. ИЗГИБ y q A B z YB z1 1 1 Подставим значения коорди-нат и рассчитаем величину
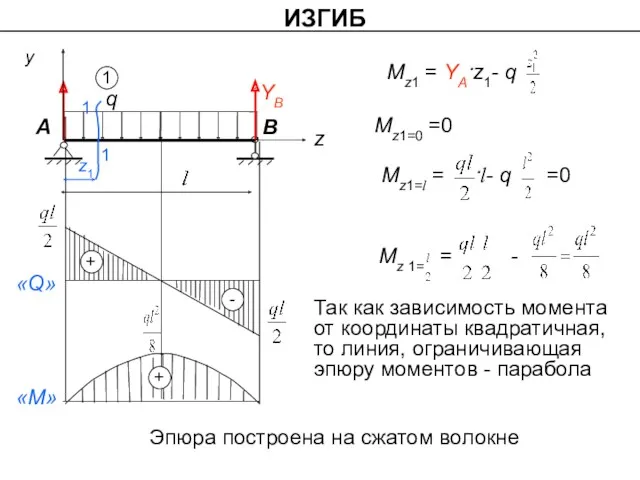
- 18. ИЗГИБ y q A B z YB z1 1 1 «Q» Mz1=0 =0 Так как зависимость
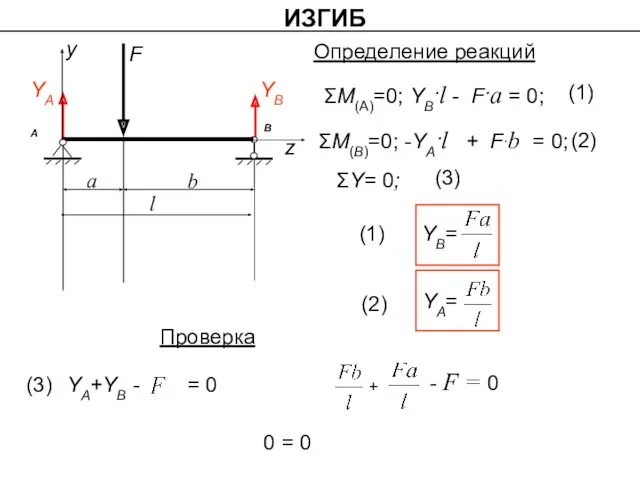
- 19. ИЗГИБ y z YA YB F ΣY= 0; (1) (2) (3) YA+YB - = 0 Проверка
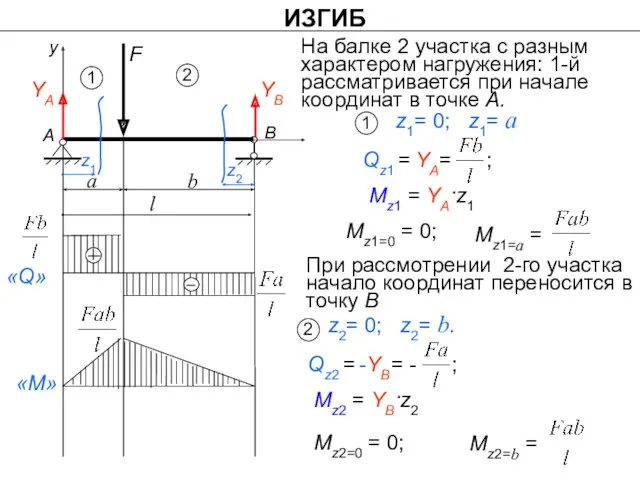
- 20. ИЗГИБ Mz1 = YA·z1 Mz2= YB·z2 Начало координат в т. В
- 21. ИЗГИБ ΣМ(А)=0; YB·l - F·a = 0; ΣY= 0; ΣМ(B)=0; -YA·l + F·b = 0; (3)
- 22. ИЗГИБ На балке 2 участка с разным характером нагружения: 1-й рассматривается при начале координат в точке
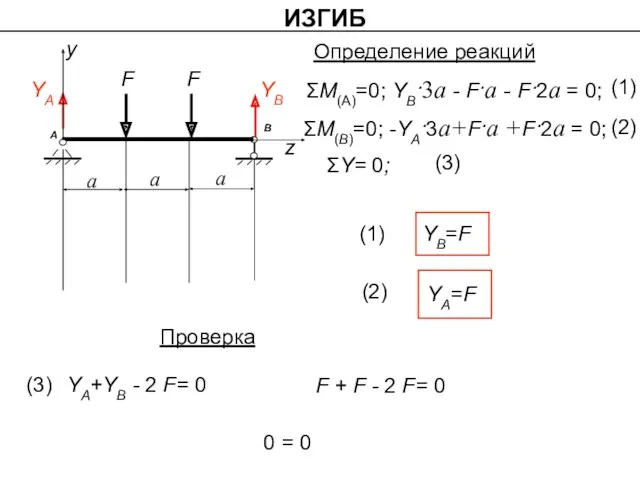
- 23. ИЗГИБ ΣМ(А)=0; YB·3а - F·a - F·2a = 0; ΣY= 0; ΣМ(B)=0; -YА·3а+F·a +F·2a = 0;
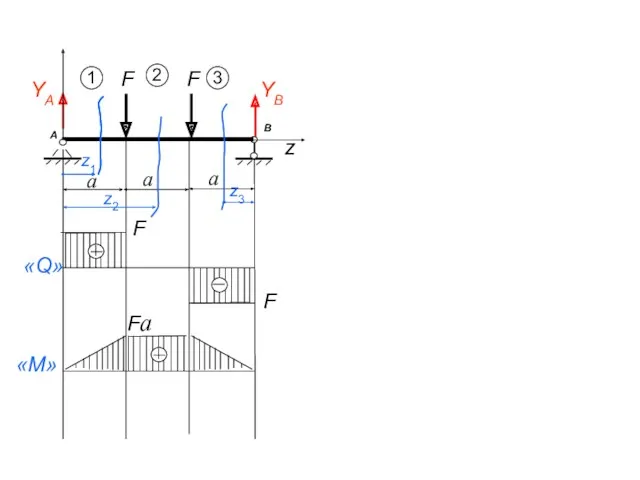
- 24. z A B YA YB F a а а F 2 3 z1 z3 z2 «Q»
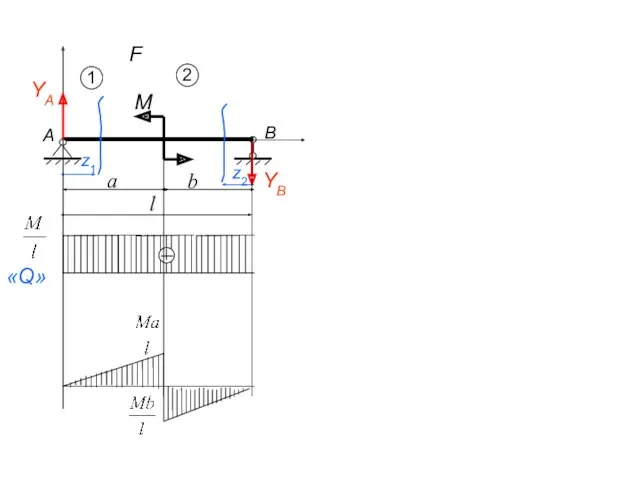
- 25. A B YA YB F 2 l a b z1 z2 «Q» М
- 26. Контрольные правила для построения эпюр поперечных сил и изгибающих моментов На концевых шарнирных опорах Qz равны
- 27. Контрольные правила для построения эпюр поперечных сил и изгибающих моментов 6. В тех сечениях, где приложены
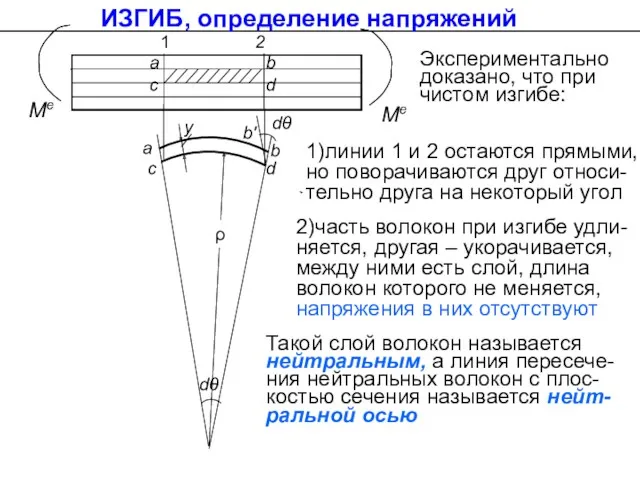
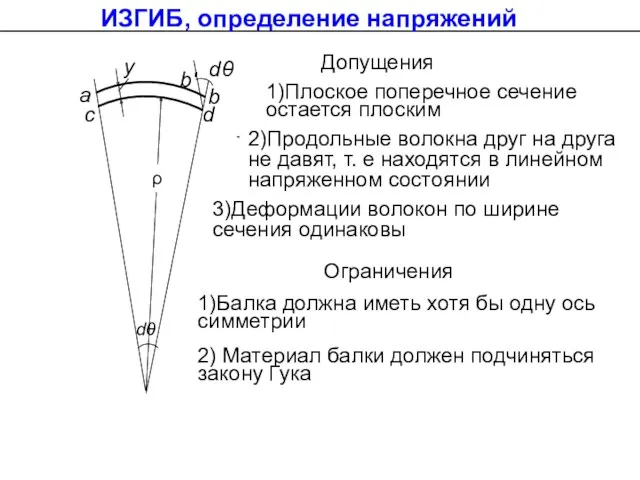
- 28. Me Me a b c d c d b b' dθ dθ ρ y a 1
- 29. c d b b' dθ dθ ρ y a Допущения 1)Плоское поперечное сечение остается плоским 2)Продольные
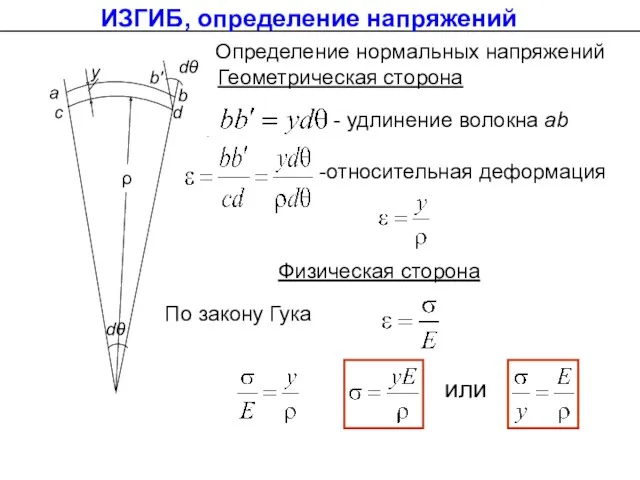
- 30. Определение нормальных напряжений Геометрическая сторона Физическая сторона По закону Гука ИЗГИБ, определение напряжений или
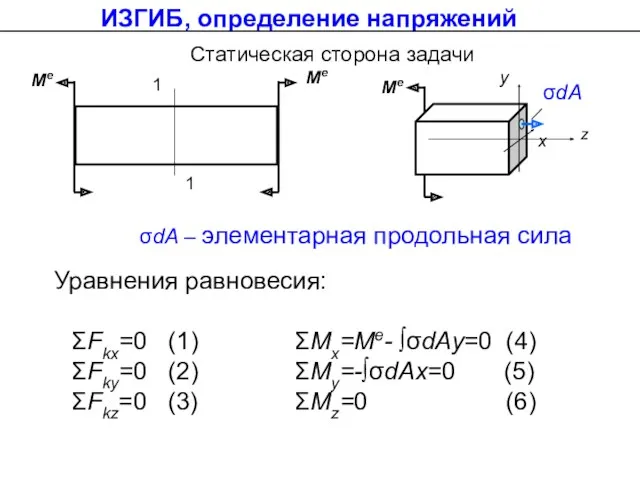
- 31. ИЗГИБ, определение напряжений Статическая сторона задачи 1 1 Ме Ме σdA – элементарная продольная сила Уравнения
- 32. ИЗГИБ, определение напряжений Вывод: Статический момент относительно оси х равен нулю, значит оси сечения являются централь-ными
- 33. Из (5), подставляя значение σ, получаем Вывод: Центробежный момент инерции равен 0, значит оси - главные
- 34. ИЗГИБ, определение напряжений Из (4), подставляя значение σ, получаем
- 35. Определение напряжений при изгибе После преобразований получены следующие выводы 1)Нейтральная ось проходит через центр сечения 2)Нейтральная
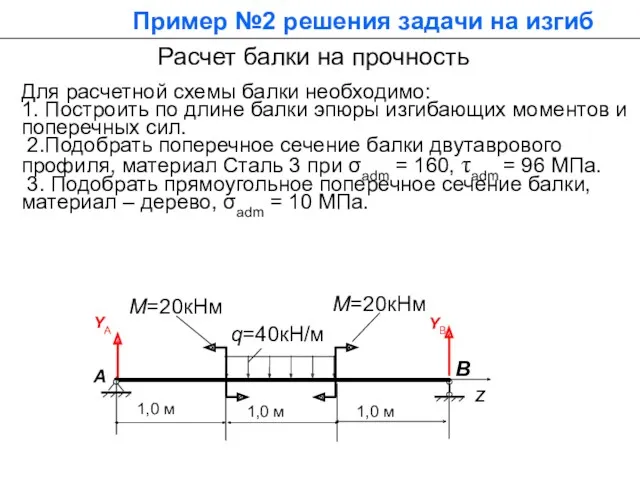
- 36. Расчет балки на прочность Для расчетной схемы балки необходимо: 1. Построить по длине балки эпюры изгибающих
- 37. YА=51,3кН YВ=42,7кН 2.Определяем реакции опор из уравнений равновесия ΣM(A)=0; M- q·4,4·2,2 - F·4,4 + YВ·6,6 =
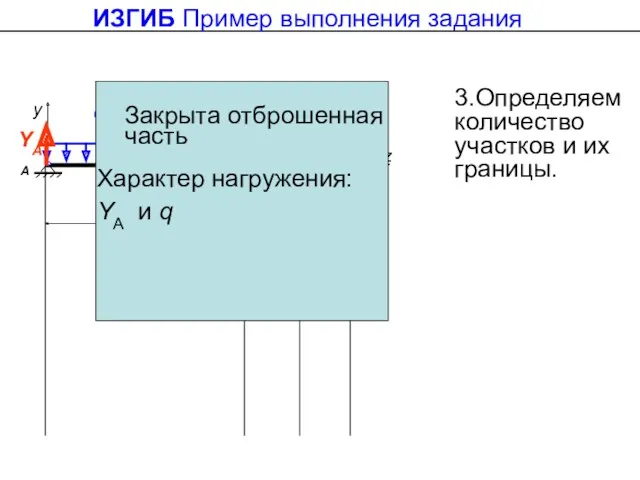
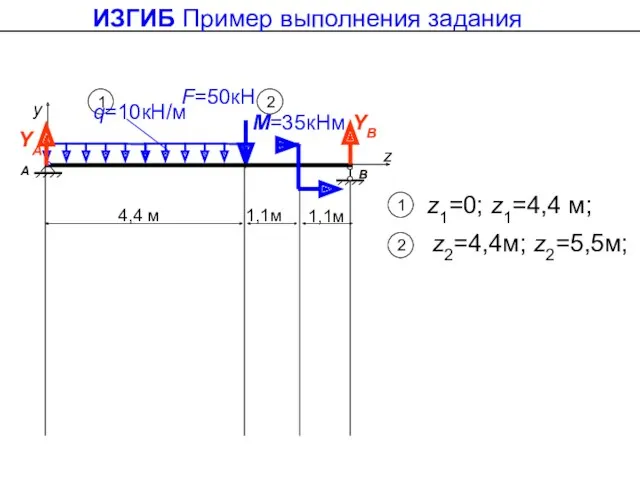
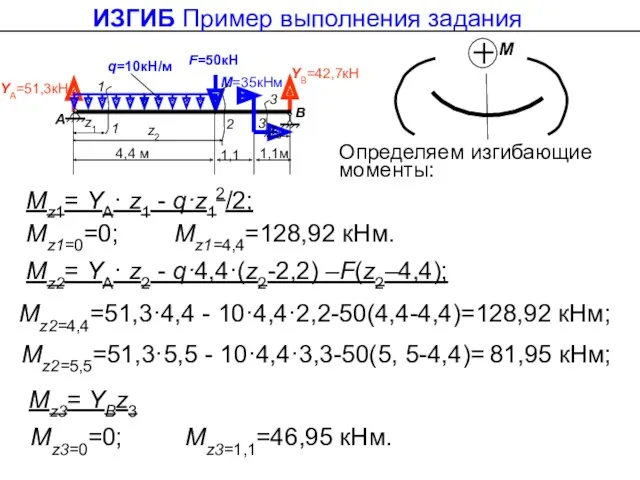
- 38. ИЗГИБ Пример выполнения задания 3.Определяем количество участков и их границы. Закрыта отброшенная часть Характер нагружения: YA
- 39. ИЗГИБ Пример выполнения задания 1 1 z1=0; z1=4,4 м; Изменился характер нагружения, добавилась сила
- 40. ИЗГИБ Пример выполнения задания 1 1 z1=0; z1=4,4 м; 2
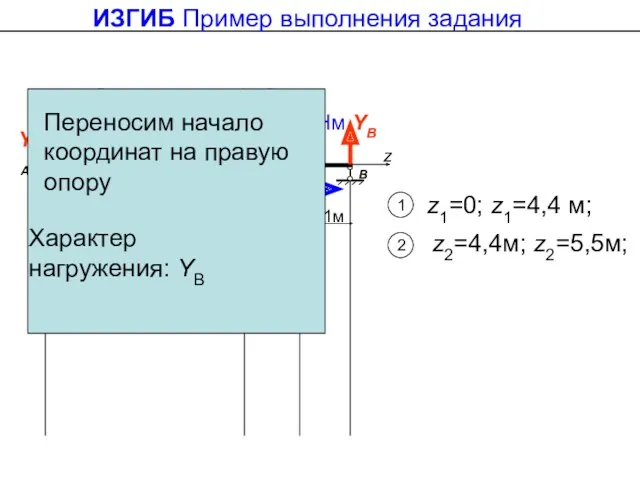
- 41. ИЗГИБ Пример выполнения задания 1 1 z1=0; z1=4,4 м; 2 Переносим начало координат на правую опору
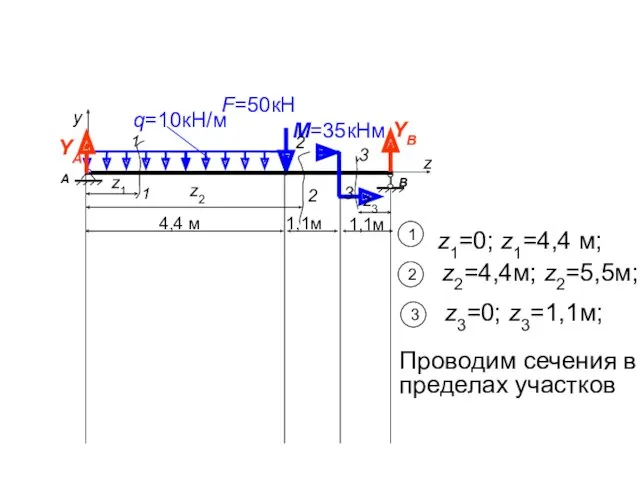
- 42. Проводим сечения в пределах участков 1 1 z1=0; z1=4,4 м;
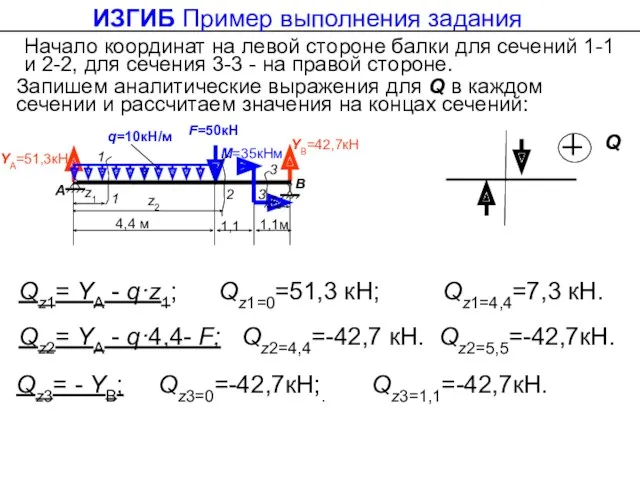
- 43. Qz3= - YВ; Qz3=0=-42,7кН;. Qz3=1,1=-42,7кН. Начало координат на левой стороне балки для сечений 1-1 и 2-2,
- 44. ИЗГИБ Пример выполнения задания Mz3= YВz3 Определяем изгибающие моменты: Mz2=5,5=51,3·5,5 - 10·4,4·3,3-50(5, 5-4,4)= 81,95 кНм; Mz2=
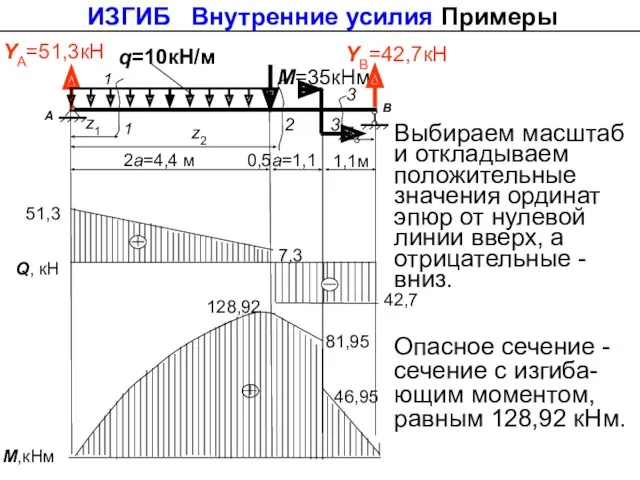
- 45. 128,92 q=10кН/м М=35кНм YА=51,3кН А В 1 2а=4,4 м YВ=42,7кН 1 z1 z2 z3 2 3
- 46. где Wн.о. – момент сопротивления относительно нейтральной оси, которая в сечении балки совпадает с осью х
- 49. а) Проверка по рабочим нормальным напряжениям: т. е. условие прочности выполняется. ИЗГИБ Пример выполнения задания
- 50. Ix - момент инерции сечения, b – толщина стенки, для двутавра b=s; б) Проверка по максимальным
- 51. Расчет балки на прочность Для расчетной схемы балки необходимо: 1. Построить по длине балки эпюры изгибающих
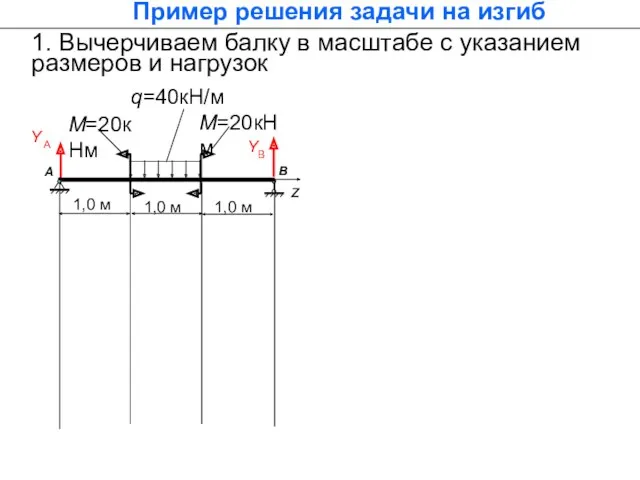
- 52. 1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок Y А q=40кН/м М=20кНм YВ М=20кНм
- 53. 2. Определяем реакции, рассматривая условие равновесия ΣУ =0; VА + VВ - q·1 = 0; 20
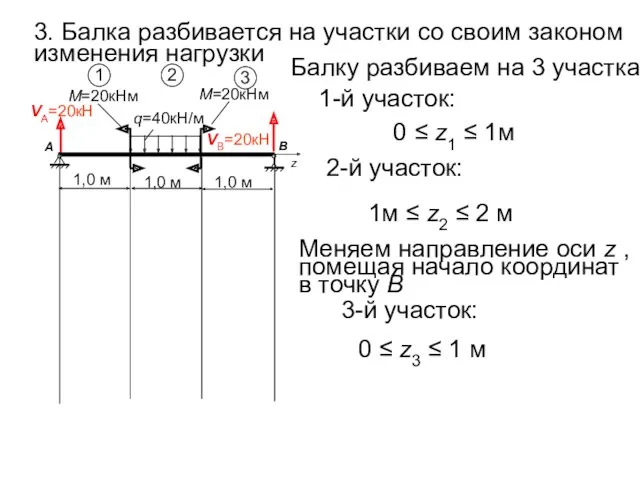
- 54. 3. Балка разбивается на участки со своим законом изменения нагрузки VА=20кН М=20кНм А 1,0 м z
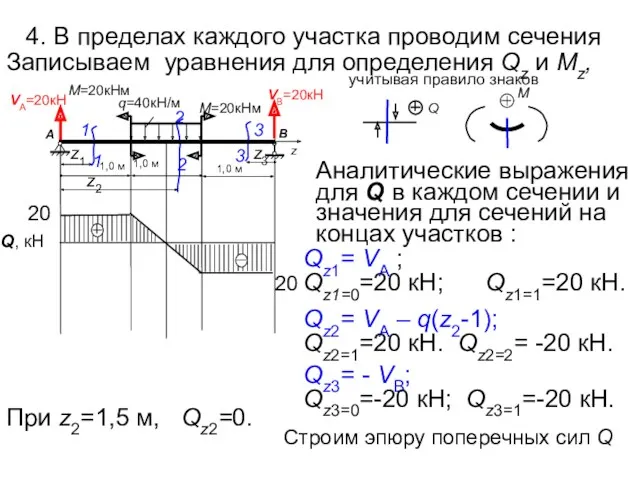
- 55. 4. В пределах каждого участка проводим сечения VВ=20кН Qz2= VА – q(z2-1); Qz2=1=20 кН. Qz2=2= -20
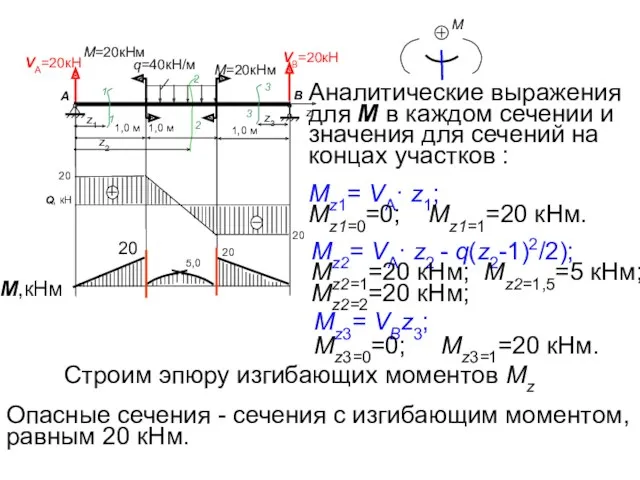
- 56. Аналитические выражения для М в каждом сечении и значения для сечений на концах участков : Mz2=
- 57. где Wн.о. – момент сопротивления относительно нейтральной оси, которая в сечении балки совпада- ет с осью
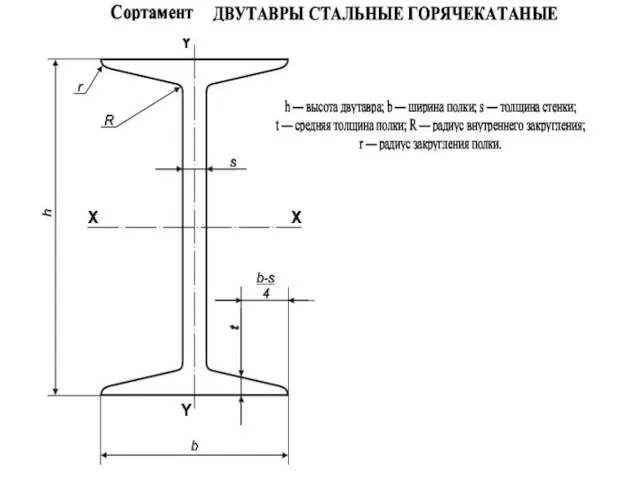
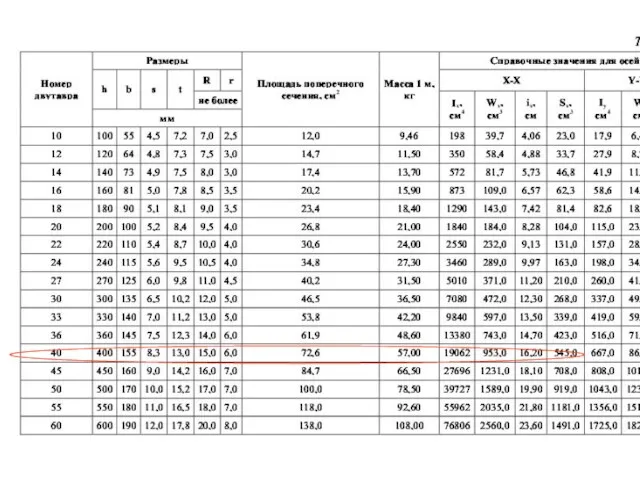
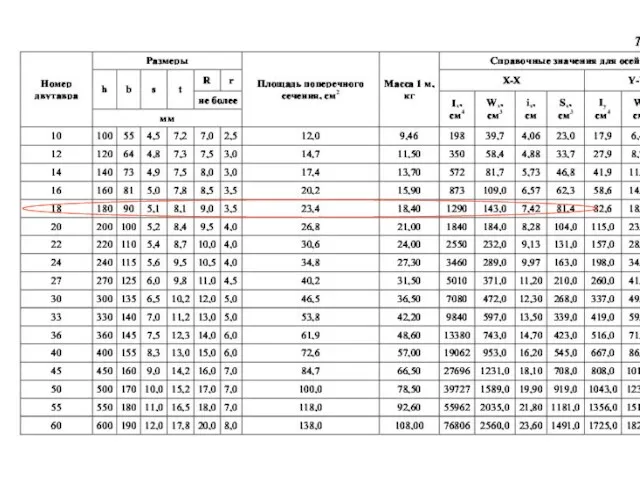
- 59. 1) Двутавровый профиль, материал Сталь 3 Ближайшее к полученному значению момента сопротивления соответствует двутавру № 18,
- 60. Проверка по рабочим напряжениям: а) нормальные напряжения т. е. условие прочности выполняется. б) максимальные касательные напряжения
- 61. 1) Прямоугольное сечение, материал дерево - момент сопротивления для прямоугольника относи- тельно оси х Учитывая заданное
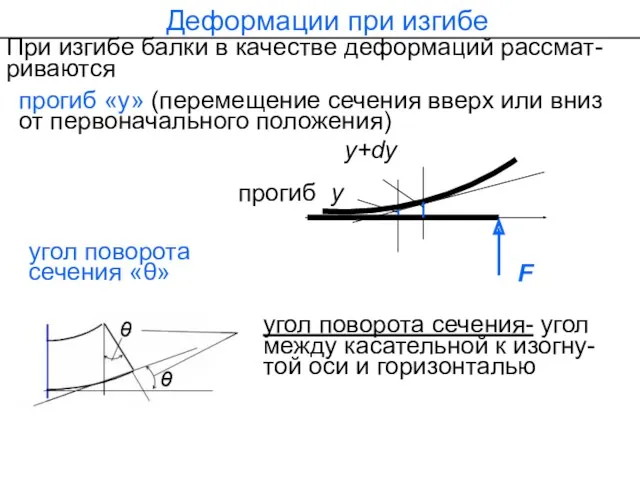
- 62. При изгибе балки в качестве деформаций рассмат-риваются Деформации при изгибе угол поворота сечения- угол между касательной
- 63. Деформации при изгибе Из математики известно уравнение для определе-ния кривизны линии и, учитывая уравнение изогнутой оси
- 64. или в виде Деформации при изгибе Интегрируя уравнение первый раз получают угол поворота сечения, второй раз
- 65. Деформации при изгибе Из этих формул сформулированы различные мето-ды определения деформаций При этом необходимо выполнять некоторые
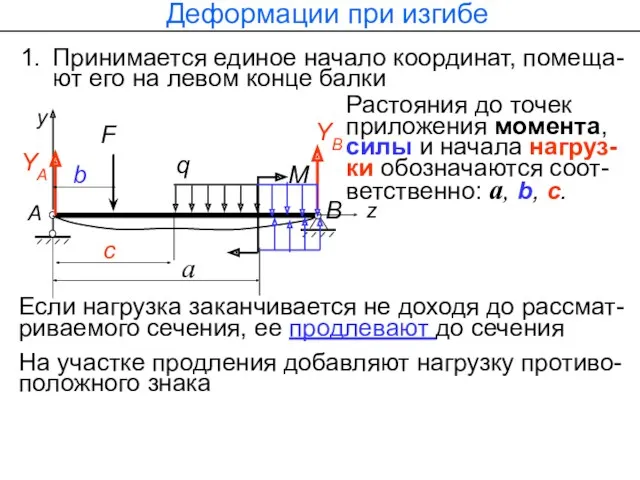
- 66. Деформации при изгибе Принимается единое начало координат, помеща-ют его на левом конце балки Растояния до точек
- 67. Универсальные уравнения для определения где θ - угол поворота в исследуемом сечении; у - прогиб в
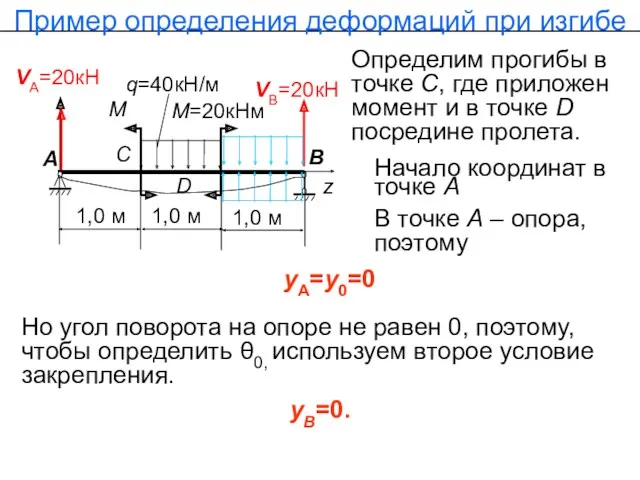
- 68. Пример определения деформаций при изгибе VА=20кН q=40кН/м М=20кНм VВ=20кН М А 1,0 м 1,0 м В
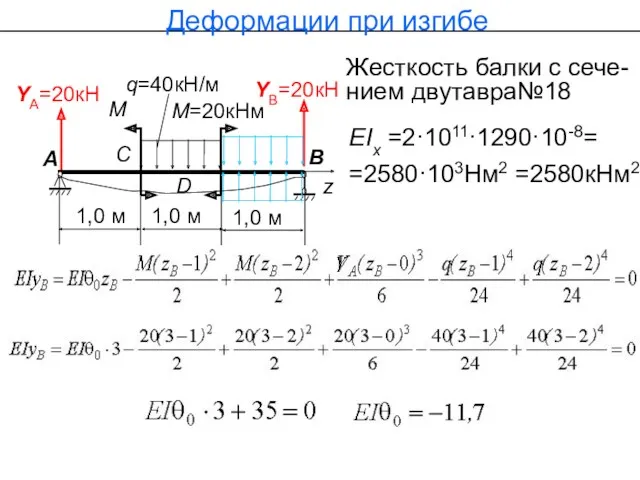
- 69. YА=20кН q=40кН/м М=20кНм YВ=20кН М А 1,0 м 1,0 м В z C D 1,0 м
- 70. Деформации при изгибе zС =1м; zD=1,5м
- 72. Скачать презентацию



























 Взаимодействие электромагнитных световых волн с веществом. Возбуждение вторичных электромагнитных волн
Взаимодействие электромагнитных световых волн с веществом. Возбуждение вторичных электромагнитных волн Работы, выполняемые на авиационной технике
Работы, выполняемые на авиационной технике Физическая игра Интеллектуальный ринг для 5- класса
Физическая игра Интеллектуальный ринг для 5- класса Тропосфера та її вплив на поширення радіохвиль
Тропосфера та її вплив на поширення радіохвиль Исследования Ломоносова, результаты которых внесли вклад в развитие учения о строении вещества и физики
Исследования Ломоносова, результаты которых внесли вклад в развитие учения о строении вещества и физики Ультразвук и инфразвук
Ультразвук и инфразвук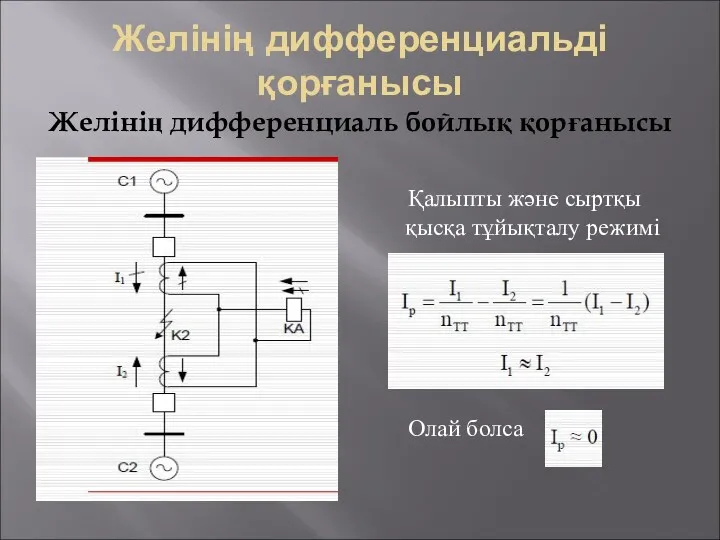 Желінің дифференциальді қорғанысы. Желінің дифференциаль бойлық қорғанысы
Желінің дифференциальді қорғанысы. Желінің дифференциаль бойлық қорғанысы Классификация методов расчета полей нейтронов и гамма-квантов. Обзор методов расчета полей нейтронов и гамма-квантов
Классификация методов расчета полей нейтронов и гамма-квантов. Обзор методов расчета полей нейтронов и гамма-квантов Физика и научный метод познания
Физика и научный метод познания Технологический процесс изготовления детали Шестерня
Технологический процесс изготовления детали Шестерня Лампы накаливания. Электронагревательные приборы
Лампы накаливания. Электронагревательные приборы Пружні деформації в тілі людини
Пружні деформації в тілі людини Исследование равноускоренного движения без начальной скорости. Лабораторная работа №1
Исследование равноускоренного движения без начальной скорости. Лабораторная работа №1 Соединения неразъемные
Соединения неразъемные Своя игра. Турнир по физике для учащихся 9 классов
Своя игра. Турнир по физике для учащихся 9 классов Вечные двигатели
Вечные двигатели Устройство сверлильного станка (технология, 5 класс)
Устройство сверлильного станка (технология, 5 класс) Датчики температуры
Датчики температуры Цепные передачи
Цепные передачи Презентации по физике
Презентации по физике Дифузія навколо нас
Дифузія навколо нас Урок в технологии критического мышления Силы в природе
Урок в технологии критического мышления Силы в природе Оптика
Оптика Рентгеновское излучение
Рентгеновское излучение Способи вивільнення ядерної енергії. 11 клас
Способи вивільнення ядерної енергії. 11 клас Шлифовальные станки. (Тема 7)
Шлифовальные станки. (Тема 7) Кванттық физика тарихы және тарихи деректерді физика пәнін оқытуда қолдану әдістемесін оқыту
Кванттық физика тарихы және тарихи деректерді физика пәнін оқытуда қолдану әдістемесін оқыту Рентгеновские лучи
Рентгеновские лучи