Содержание
- 2. Механика- это раздел физики, в котором изучается простейшая форма движения материи – механическое, т.е. движение тел
- 3. Основные понятия классической механики Положение тела в пространстве может быть определено только по отношению к каким-либо
- 4. Тело, которое служит для определения положения интересующего нас тела называют телом отсчёта. Для описания движения с
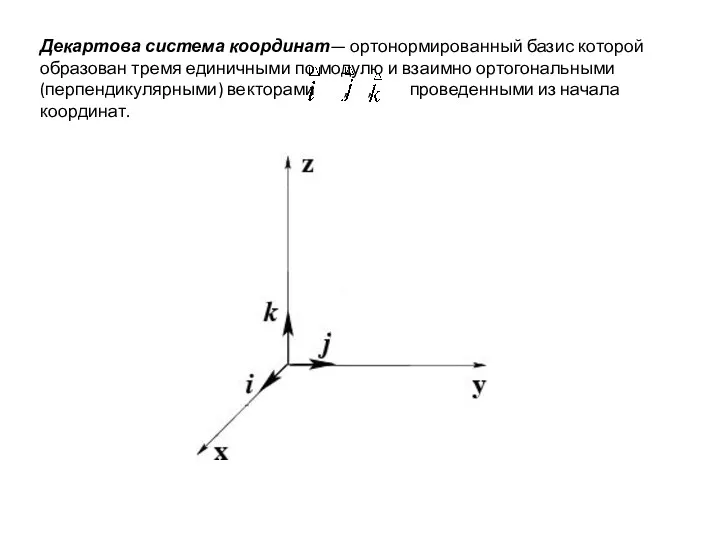
- 5. Декартова система координат— ортонормированный базис которой образован тремя единичными по модулю и взаимно ортогональными (перпендикулярными) векторами
- 6. Ньютоновская механика- основана на основанный на законах Ньютона и принципе относительности Галилея: скорости тел малы по
- 7. Задачи механики Изучение различных движений и обобщение полученных результатов в виде законов движения- законов, с помощью
- 8. Кинематика- это раздел механики, где изучаются различные способы описания движений независимо от причин, обуславливающих эти движения.
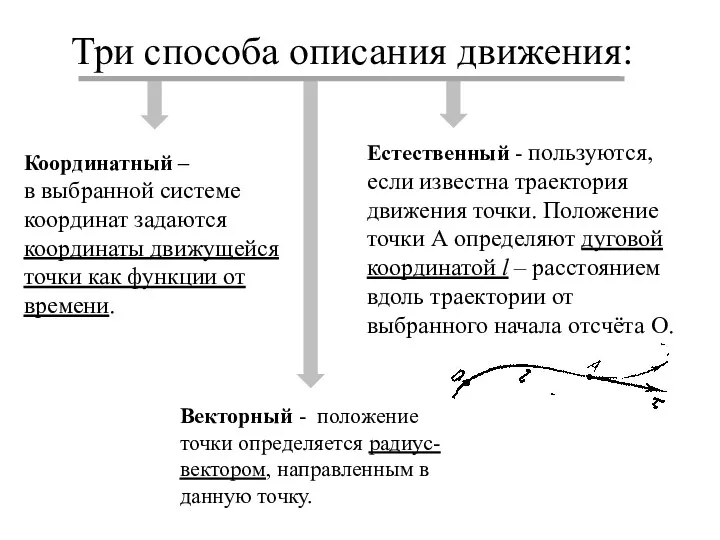
- 9. Три способа описания движения: Координатный – в выбранной системе координат задаются координаты движущейся точки как функции
- 10. Векторный способ Положение точки задают радиус-вектором r. При движении точки радиус-вектор меняется по модулю и направлению,
- 11. Скорость — это векторная величина, которая определяет быстроту и направление движения в данный момент времени [м/с].
- 12. Ускорение a определяет скорость изменения вектора скорости (по модулю и направлению) точки со временем равен производной
- 13. Обратная задача, можно найти v(t) и r(t) зная зависимость a(t) ? Достаточно ли начальных условий: v0
- 14. Рассмотрим случай равноускоренного движения a = const. Найдём v(t). За промежуток времени dt элементарное приращение скорости
- 15. Найдём радиус-вектор: за промежуток времени dt элементарное приращение радиус-вектора dr: dr = v * dt. Интегрируем
- 16. Тогда сам радиус вектор r: r = r0 + ∆r= r0 + v0 t+ a t2/2
- 17. С выбранным телом отсчёта жестко связывают определённую систему координат, например, декартову. Запишем в момент времени t
- 18. Проекции векторов скорости и ускорения: vx =dx/dt vy =dy/dt vz =dz/dt ax =dvx /dt = d2x/dt2
- 19. При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по
- 20. Введём единичный вектор ?, связанный с движущейся точкой А и направленный по касательной к траектории в
- 21. Преобразуем: v?(d?/dt) = v?(d? * dl/dt * dl)= v?2 d? /dl= v2d? /dl (1) Тангенциальное и
- 22. dτ Угол δα = ׀dl׀ / ρ Введём единичный вектор нормали n к траектории в точке
- 24. Скачать презентацию



















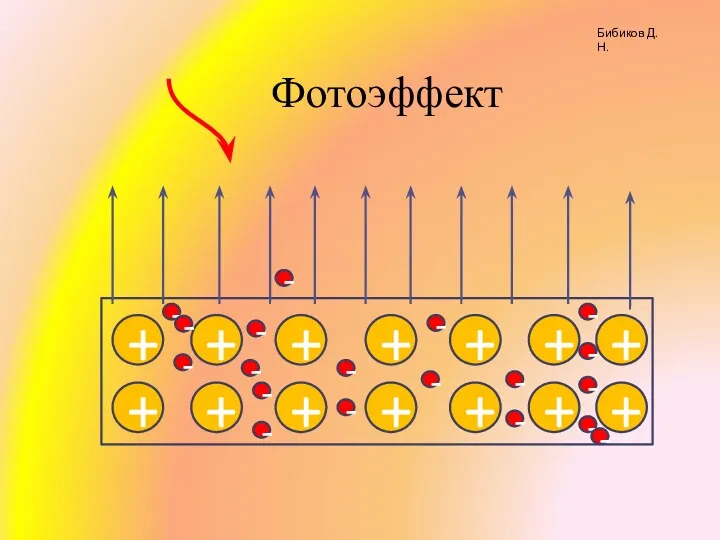 Фотоэффект
Фотоэффект Инструментальные методы анализа. Классификация методов
Инструментальные методы анализа. Классификация методов Нелинейная восприимчивость третьего порядка и четырехволновые взаимодействия. Лекция 5
Нелинейная восприимчивость третьего порядка и четырехволновые взаимодействия. Лекция 5 Презентация к уроку Кипение 8 класс.
Презентация к уроку Кипение 8 класс. Явление электромагнитной индукции
Явление электромагнитной индукции Презентация к уроку Электрический ток
Презентация к уроку Электрический ток презентация Атмосферное давление
презентация Атмосферное давление Диэлектрики и проводники в электрическом поле
Диэлектрики и проводники в электрическом поле Закон Кулона
Закон Кулона Презентация урока в 7 классе по теме Простые механизмы. Рычаг. Условие равновесия рычага.
Презентация урока в 7 классе по теме Простые механизмы. Рычаг. Условие равновесия рычага. Автосцепные устройства
Автосцепные устройства Подвеска колес автомобиля
Подвеска колес автомобиля Трансформатор. Передача электрической энергии на расстояние
Трансформатор. Передача электрической энергии на расстояние Излучение и спектры (презентация)
Излучение и спектры (презентация) Спуск с орбиты космических аппаратов
Спуск с орбиты космических аппаратов Четвёртое состояние вещества. Плазма
Четвёртое состояние вещества. Плазма Электрическое поле. (лекция 1а)
Электрическое поле. (лекция 1а) Проектирование масштабных моделей в технике простого занижения. (4 класс)
Проектирование масштабных моделей в технике простого занижения. (4 класс) Электризация тел. Взаимодействие тел. Два вида зарядов
Электризация тел. Взаимодействие тел. Два вида зарядов Электричество. Задачи и схемы
Электричество. Задачи и схемы Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1
Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа №1 Теплотехника. Теоретические основы. Теплосиловое оборудование
Теплотехника. Теоретические основы. Теплосиловое оборудование Техника безопасности при работе с электрическим током. Проблемы энергосбережения
Техника безопасности при работе с электрическим током. Проблемы энергосбережения Атомно-абсорбционная спектрометрия
Атомно-абсорбционная спектрометрия Конусні дробарки
Конусні дробарки Петрофизика. Коллектроские свойства горных пород
Петрофизика. Коллектроские свойства горных пород ”Движение по окружности”
”Движение по окружности” Свободное падение тел. 9 класс
Свободное падение тел. 9 класс