Содержание
- 2. Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Процесс распространения колебаний в пространстве
- 3. По характеру воздействия на колебательную систему выделяют: Свободные (или собственные) колебания – колебания, совершаемые за счет
- 4. Механические колебания и волны Гармонические колебания и их характеристики Колебаниями называются движения или процессы, которые характеризуются
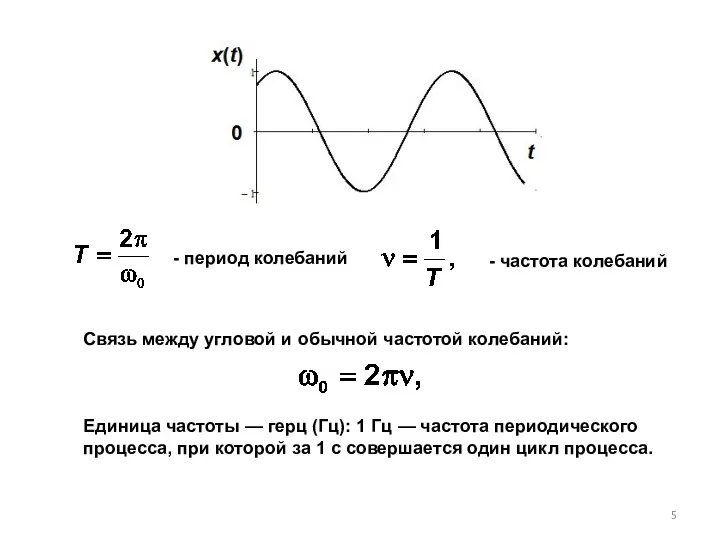
- 5. - период колебаний - частота колебаний Связь между угловой и обычной частотой колебаний: Единица частоты —
- 6. Дифференциальное уравнение гармонических колебаний: Решение дифференциального уравнения:
- 7. Гармонический осциллятор. Пружинный, физический и математический маятники Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида;
- 8. Уравнение движения маятника: Пружинный маятник совершает гармонические колебания по закону: с циклической частотой и периодом
- 9. 2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной
- 10. Уравнение динамики физического маятника: или: где: Решение динамического уравнения:
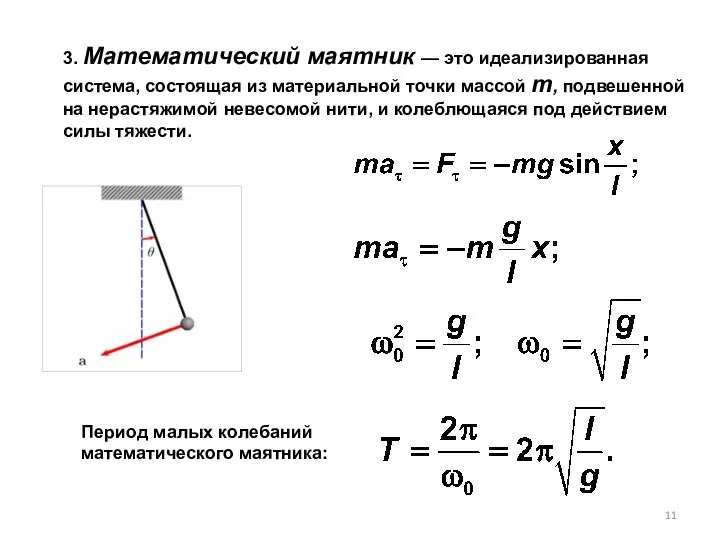
- 11. 3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой
- 12. Характеристики колебаний:
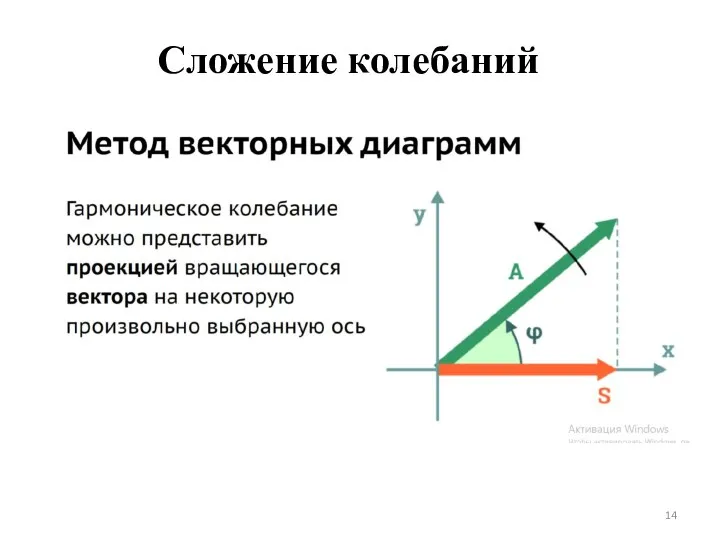
- 14. Сложение колебаний
- 15. Для дальнейшего рассмотрения теории колебаний вспомним некоторые моменты теории комплексных переменных
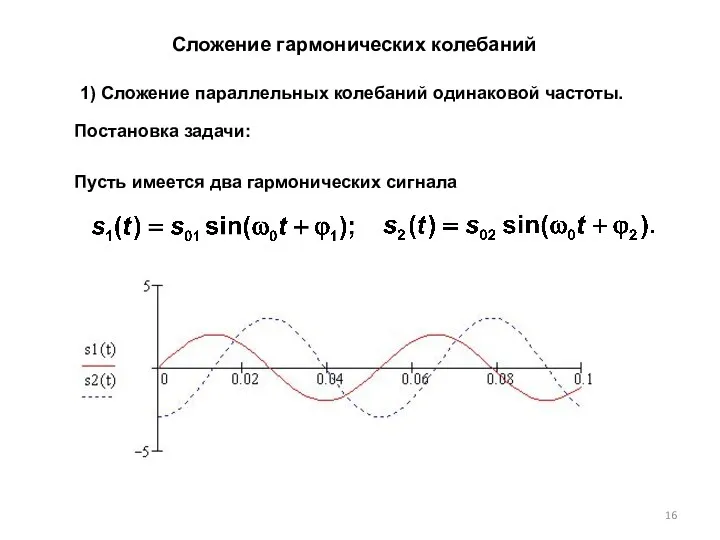
- 16. 1) Сложение параллельных колебаний одинаковой частоты. Пусть имеется два гармонических сигнала Постановка задачи: Сложение гармонических колебаний
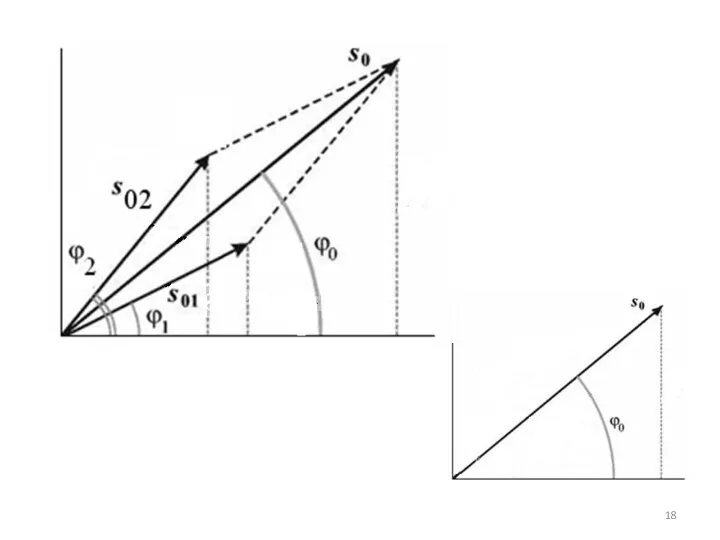
- 17. Необходимо сложить два колебания с одинаковыми частотами:
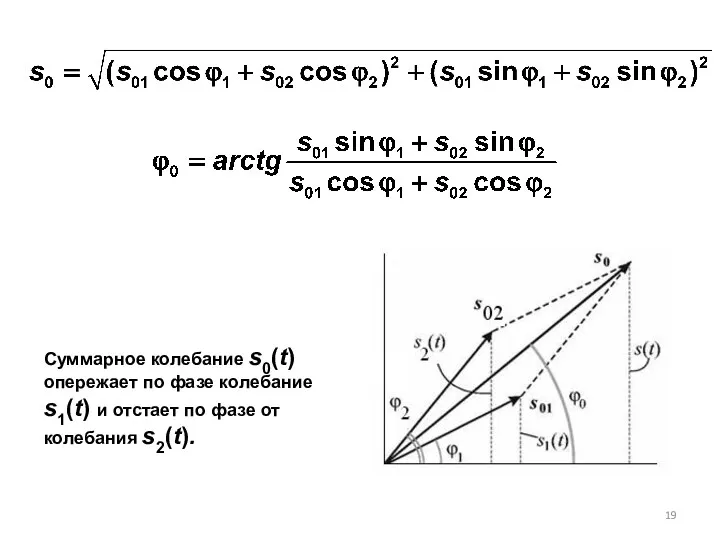
- 19. Суммарное колебание s0(t) опережает по фазе колебание s1(t) и отстает по фазе от колебания s2(t).
- 20. 2) Сложение параллельных гармонических колебаний с близкими частотами. Найдем сумму двух гармонических колебаний, частоты которых различны,
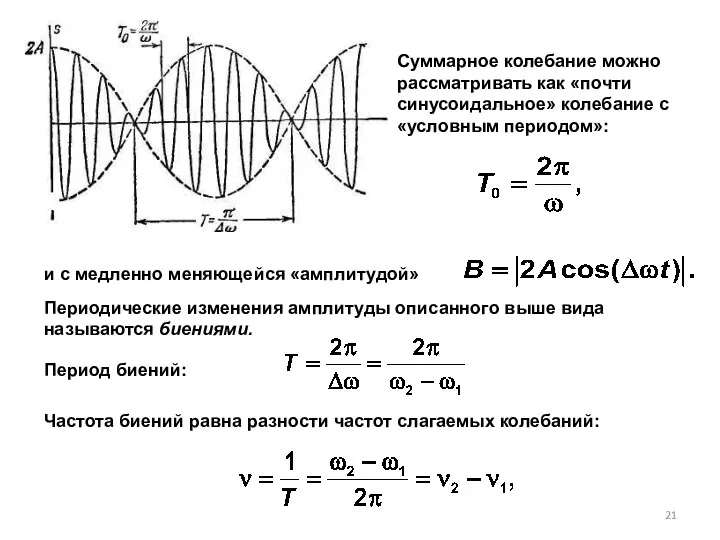
- 21. Суммарное колебание можно рассматривать как «почти синусоидальное» колебание с «условным периодом»: и с медленно меняющейся «амплитудой»
- 22. Чтобы получить траекторию движения, исключим из выражений текущее время и преобразуем синус по формулам тригонометрии: 3)
- 23. Умножим первое уравнение на cos φ2, а второе — на cos φ1 и вычтем второе уравнение
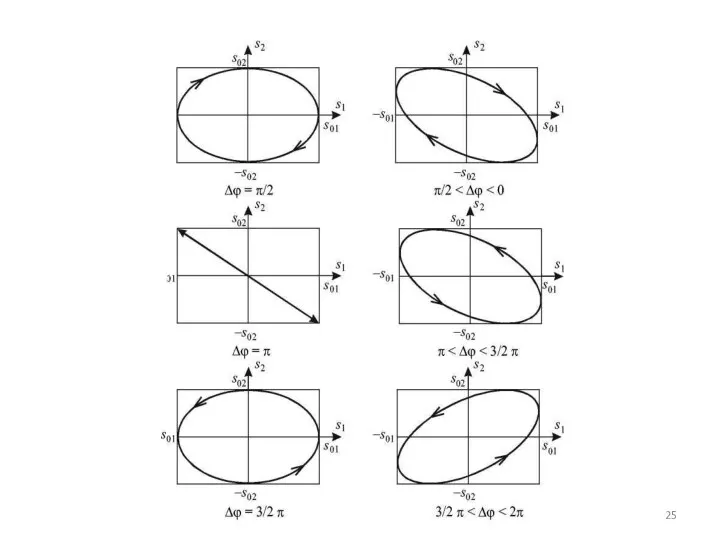
- 24. В результате будут совершатьcя периодические движения по эллиптической траектории. Направление движения вдоль траектории и ориентация эллипса
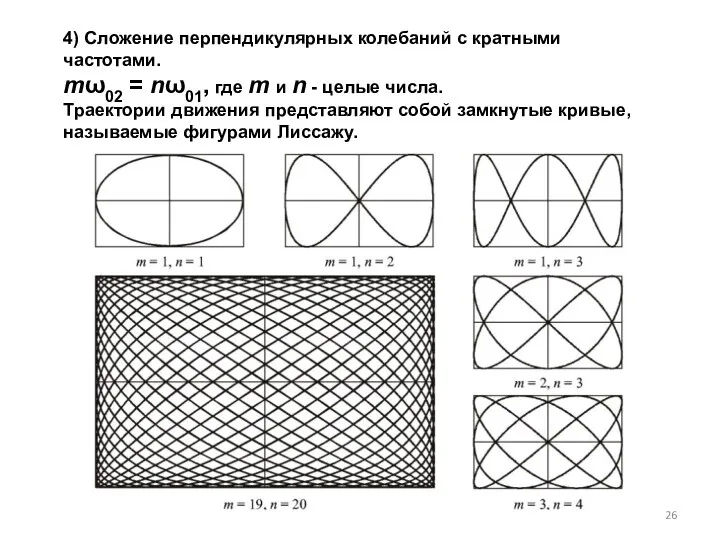
- 26. 4) Сложение перпендикулярных колебаний с кратными частотами. mω02 = nω01, где m и n - целые
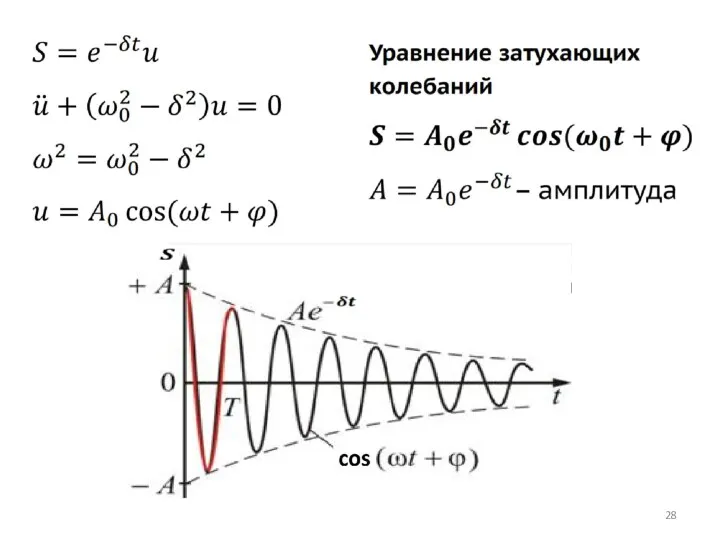
- 27. Затухающие колебания происходят в замкнутой механической системе (Fвнеш=0), в которой имеются потери энергии на преодоление сил
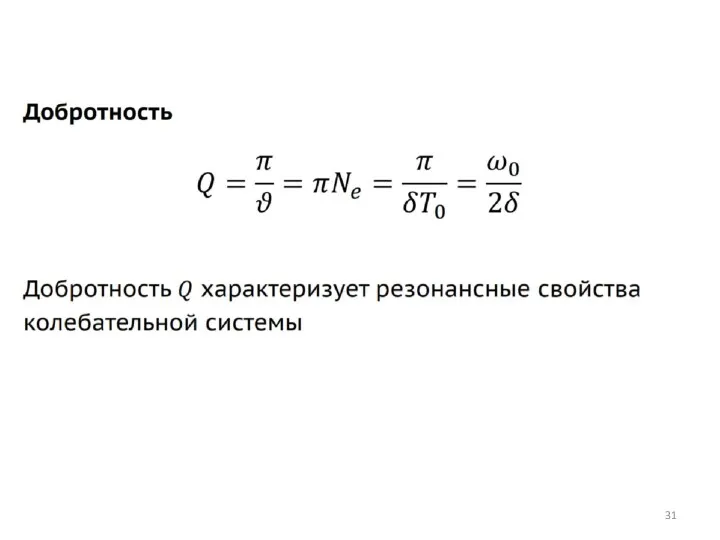
- 29. Характеристики затухающих колебаний
- 33. Для получения незатухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая подталкивала бы тело то в
- 37. Электромагнитные колебания. Свободные электромагнитные колебания. Электрический колебательный контур. Формула Томсона. Электромагнитные колебания могут возникать в цепи,
- 38. Если ввести обозначение , то полученное уравнение принимает вид: . Решением этого уравнения, как известно, является
- 39. Сопоставляя полученные выражения, видим, что когда напряжение на конденсаторе, а значит энергия электрического поля, обращается в
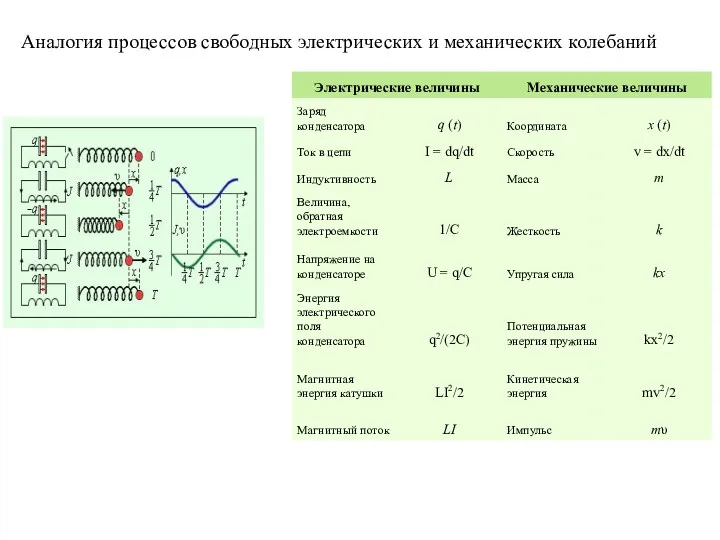
- 40. Аналогия процессов свободных электрических и механических колебаний
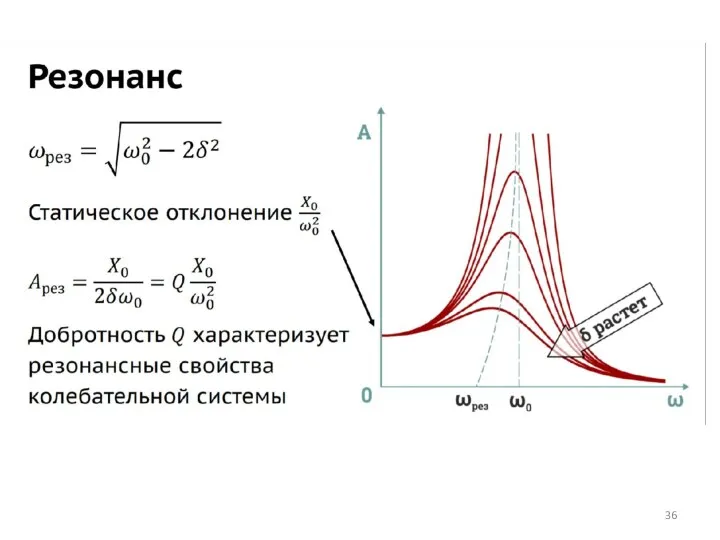
- 41. Свободные затухающие колебания. Добротность колебательного контура. Всякий реальный колебательный контур обладает сопротивлением. Энергия электрических колебаний в
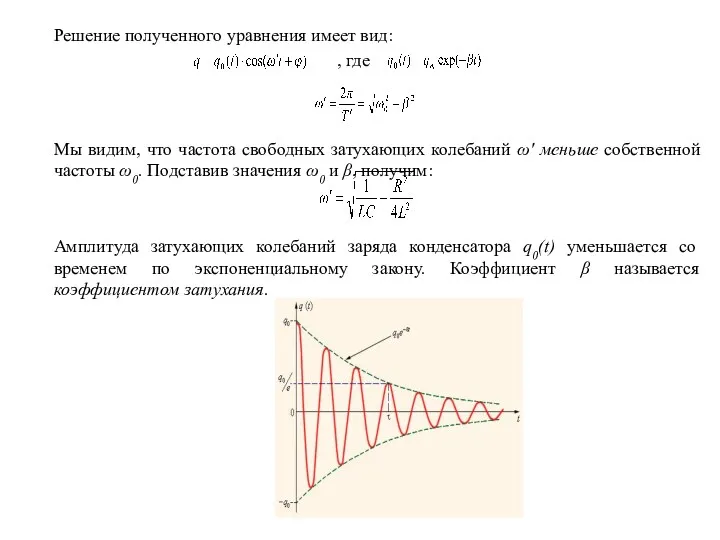
- 42. Решение полученного уравнения имеет вид: , где Мы видим, что частота свободных затухающих колебаний ω′ меньше
- 43. Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как: . Легко видеть, что декремент колебаний обратен
- 44. Вынужденные электрические колебания Если в цепь электрического контура, содержащего емкость, индуктивность и сопротивление, включить источник переменной
- 45. Интересующее нас частное решение этого дифференциального уравнения имеет вид: где Решение соответствующего однородного уравнения, представляет собой
- 46. Напряжение на сопротивлении R: , . Напряжение на конденсаторе С: , . Напряжение на катушке индуктивности
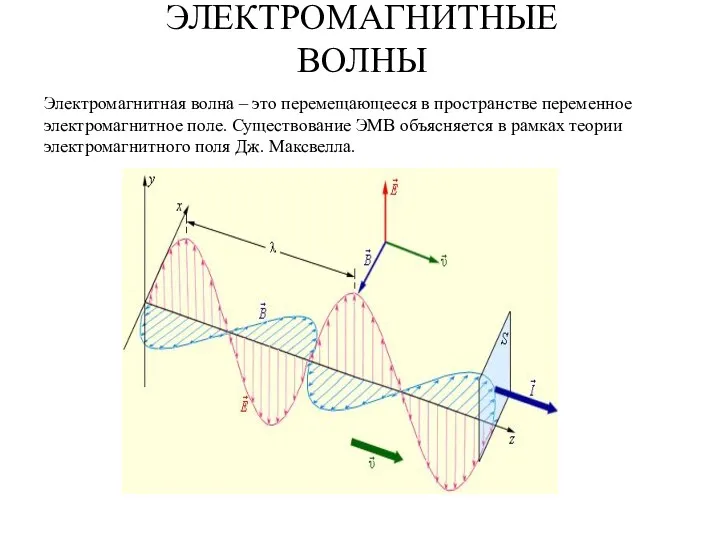
- 57. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ Электромагнитная волна – это перемещающееся в пространстве переменное электромагнитное поле. Существование ЭМВ объясняется в
- 58. Свойства электромагнитных волн Э/м волны поперечны Э/м волны распространяются со скоростью Объемные плотности электрического и магнитного
- 60. Скачать презентацию





















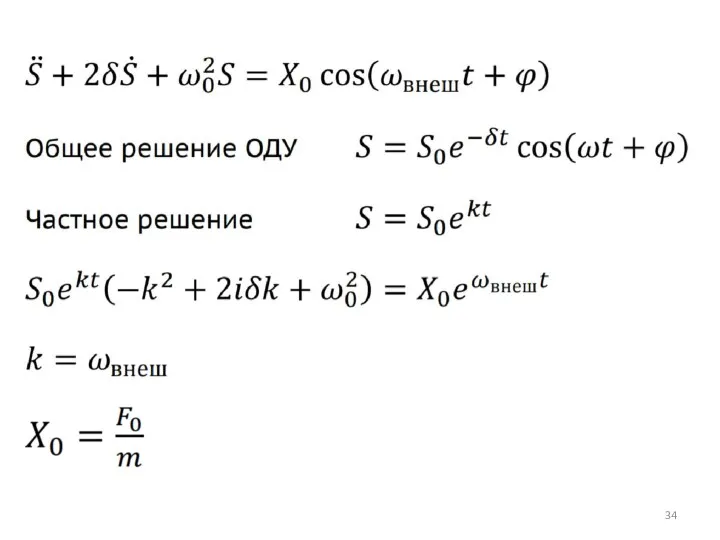


















 Электрический ток в растворах и расплавах электролитов
Электрический ток в растворах и расплавах электролитов Импульс. Закон сохранения импульса
Импульс. Закон сохранения импульса Слайды. Полупроводниковые материалы. (Лекция 6)
Слайды. Полупроводниковые материалы. (Лекция 6) Механическая энергия. Кинетическая и потенциальная энергия. Закон сохранения энергии
Механическая энергия. Кинетическая и потенциальная энергия. Закон сохранения энергии Презентация к уроку физики в 7 классе по теме Сообщающиеся сосуды
Презентация к уроку физики в 7 классе по теме Сообщающиеся сосуды Механика материалов
Механика материалов Они приближали победу
Они приближали победу Динамика. Законы Ньютона. 10 класс
Динамика. Законы Ньютона. 10 класс Технология ремонта машин. Решение задач
Технология ремонта машин. Решение задач Спектр және спектрлік анализ
Спектр және спектрлік анализ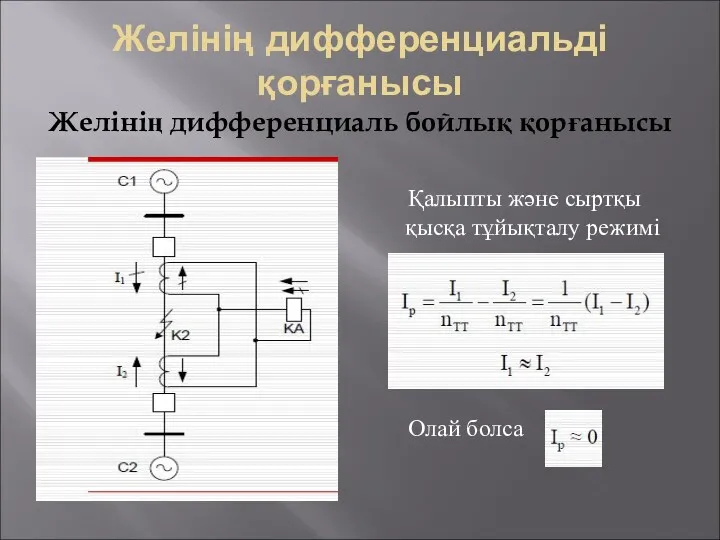 Желінің дифференциальді қорғанысы. Желінің дифференциаль бойлық қорғанысы
Желінің дифференциальді қорғанысы. Желінің дифференциаль бойлық қорғанысы Kinematika. Милдеттер
Kinematika. Милдеттер Решение задач по кинематике.
Решение задач по кинематике. Характеристики відцентрових насосів
Характеристики відцентрових насосів Системы запуска газотурбинных двигателей (ГТД )
Системы запуска газотурбинных двигателей (ГТД ) Актуальные вопросы подготовки к ЕГЭ по физике
Актуальные вопросы подготовки к ЕГЭ по физике Вес тела. Сила тяжести. Динамометр
Вес тела. Сила тяжести. Динамометр Механические характеристики металлов
Механические характеристики металлов Буксы. Общие сведения
Буксы. Общие сведения Инструментальные методы исследования органических веществ. Спектроскопические методы – ЯМР 13C
Инструментальные методы исследования органических веществ. Спектроскопические методы – ЯМР 13C Вильгельм Конрад Рентген
Вильгельм Конрад Рентген Конструктивные особенности шинопроводов и токопроводов. Технология монтажа шинопроводов и токопроводов
Конструктивные особенности шинопроводов и токопроводов. Технология монтажа шинопроводов и токопроводов Презентация по теме: Механические колебания
Презентация по теме: Механические колебания Разработка установки для замены масла в двигателе
Разработка установки для замены масла в двигателе Биологическое действие радиации. Закон радиоактивного распада
Биологическое действие радиации. Закон радиоактивного распада Критические параметры реактора
Критические параметры реактора Автомобильные аккумуляторные батареи
Автомобильные аккумуляторные батареи Электрические явления в природе
Электрические явления в природе