Содержание
- 2. Шекті топтарды қорыту принципі нүктелік симметрия топтарын қорыту принципіне ұқсас. Шекті топтарды нүктелік топтар сияқты стереографиялық
- 3. Қарапайым ∞ класта ерекше бағыт бойымен өтетін реті ∞ тең айналу осі бар. ∞ шекті тобын
- 4. ∞ айналу осіне симметрия жазықтығын қосайық. Алдымен жазықтық оське перпендикуляр орналасқан болсын. Бұл жағдайда ∞/m тобын
- 5. Енді симметрия жазықтығы оське параллель орналасқан болсын. Бұл жағдайда келесі топты табамыз: ∞m = ∞m∞ =
- 6. ∞/mm тобын қозғалмайтын цилиндр көмегімен бейнелейді. Цилиндр осінің бойымен ∞ осі өтеді, оған параллель симметрия жазықтықтарының
- 7. Біріншісі – ∞/∞ – жарықтың поляризация жазықтығын айналдыратын оптикалық активті заттан жасалған шар болып табылады. Шардың
- 8. Шекті симметрия топтарын зерттеген кезде нүктелік симметрия топтарының шағын топшалары деп аталатын жаңа маңызды үғым енгізіледі.
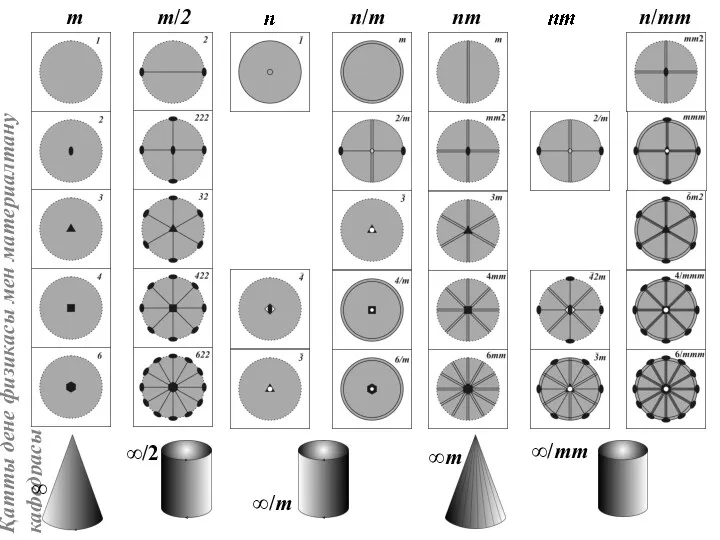
- 9. ∞/2 ∞m т т/2 n/m nm n/mm
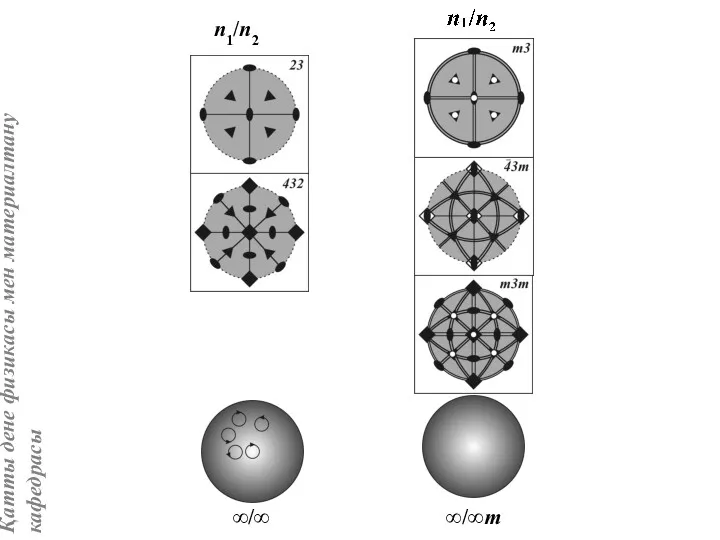
- 10. n1/n2 ∞/∞ ∞/∞m
- 11. Шекті топтар өзара топтар және топшалар арасындағы қатынастармен байланысады. Топша ұғымын кеңістік фигуралардың барлық нүктелік топтарына
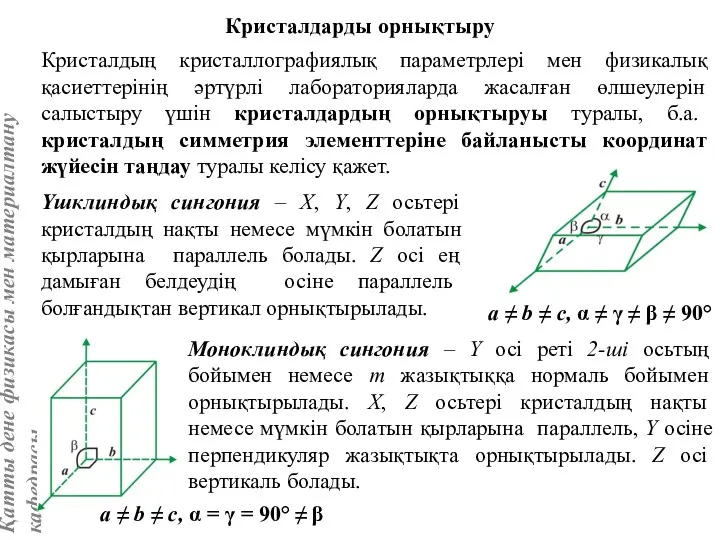
- 12. Кристалдың кристаллографиялық параметрлері мен физикалық қасиеттерінің әртүрлі лабораторияларда жасалған өлшеулерін салыстыру үшін кристалдардың орнықтыруы туралы, б.а.
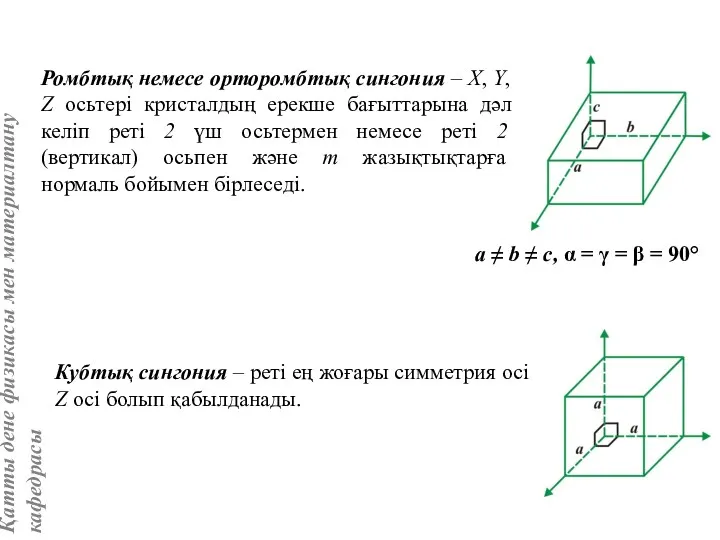
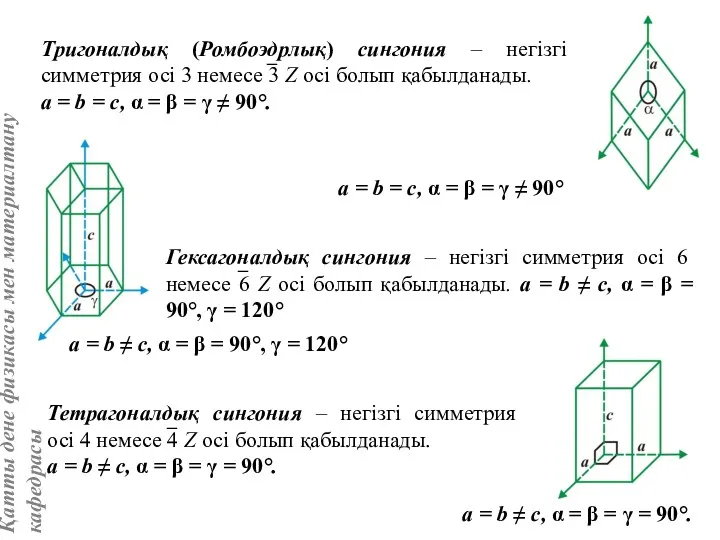
- 13. Ромбтық немесе орторомбтық сингония – X, Y, Z осьтері кристалдың ерекше бағыттарына дәл келіп реті 2
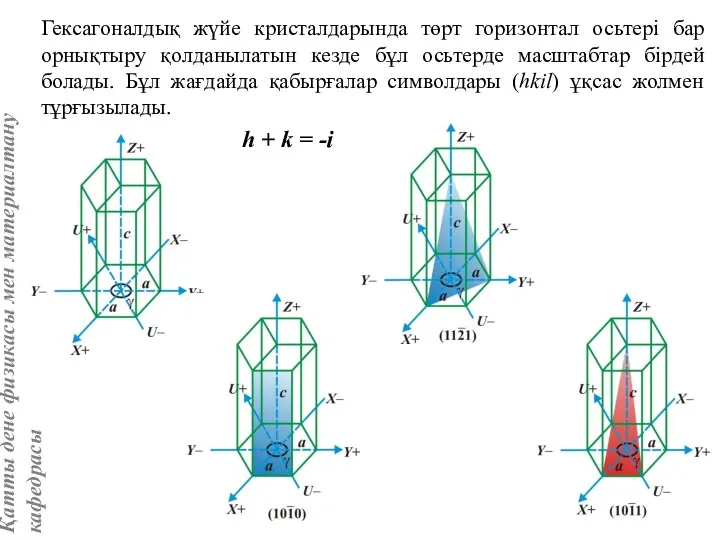
- 15. h + k = -i Гексагоналдық жүйе кристалдарында төрт горизонтал осьтері бар орнықтыру қолданылатын кезде бұл
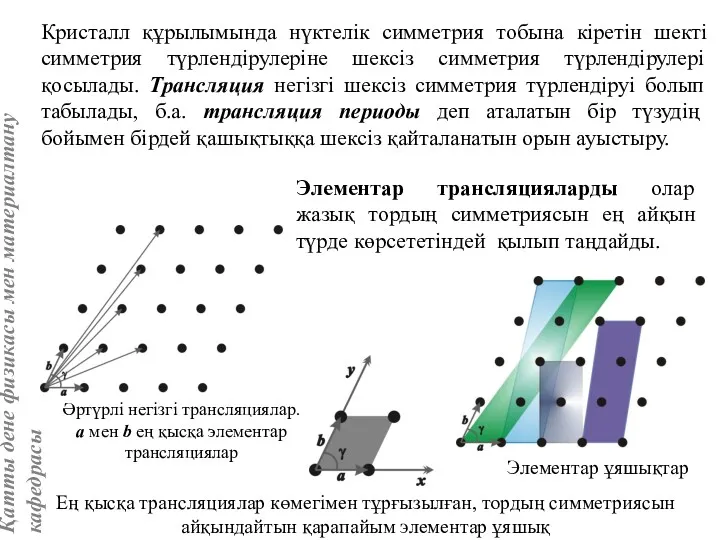
- 16. Кристалл құрылымында нүктелік симметрия тобына кіретін шекті симметрия түрлендірулеріне шексіз симметрия түрлендірулері қосылады. Трансляция негізгі шексіз
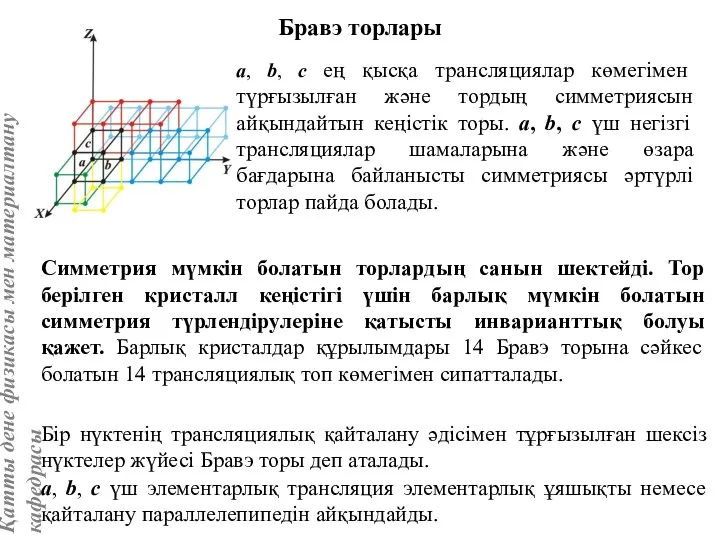
- 17. a, b, c ең қысқа трансляциялар көмегімен түрғызылған және тордың симметриясын айқындайтын кеңістік торы. а, b,
- 18. Екіөлшемдік торлар үшін Бравэ торларын қорыту принципі 14 Бравэ торы бір бірінен элементар ұяшықтарының пішіні мен
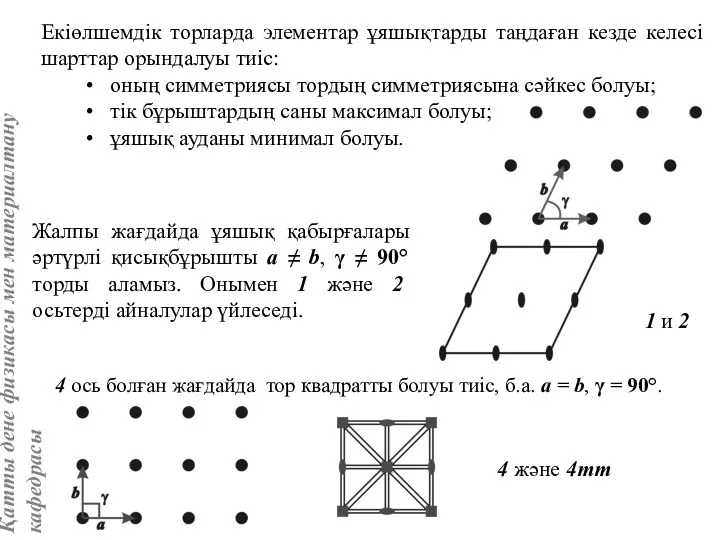
- 19. Жалпы жағдайда ұяшық қабырғалары әртүрлі қисықбұрышты а ≠ b, γ ≠ 90° торды аламыз. Онымен 1
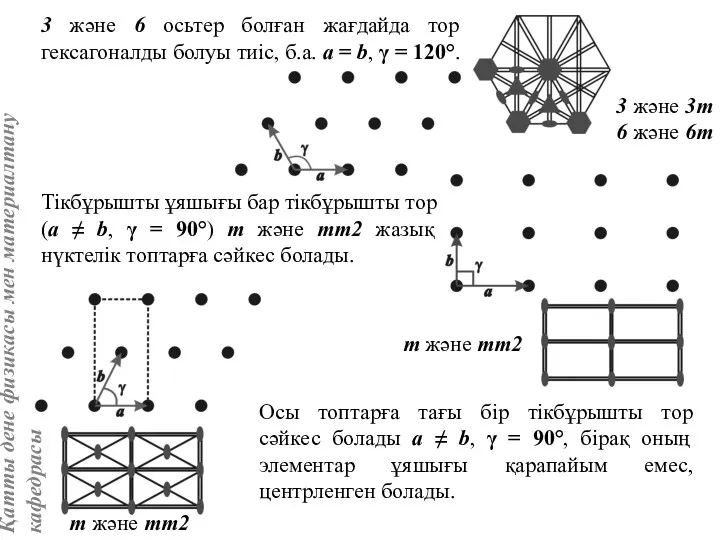
- 20. 3 және 6 осьтер болған жағдайда тор гексагоналды болуы тиіс, б.а. а = b, γ =
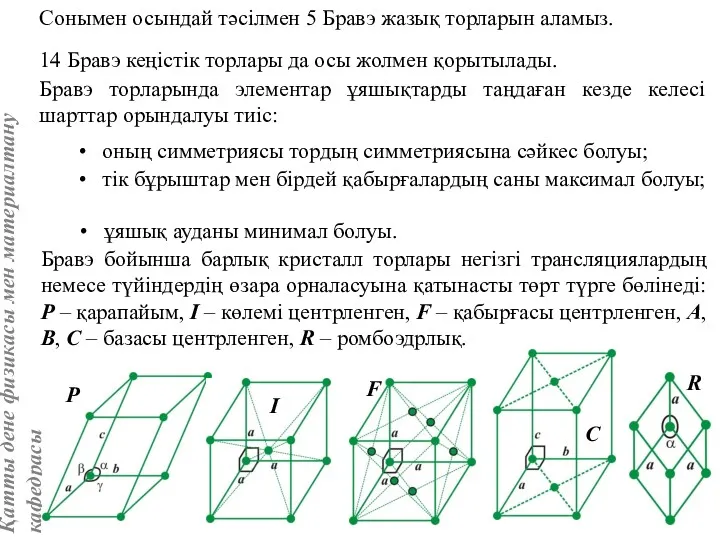
- 21. Бравэ торларында элементар ұяшықтарды таңдаған кезде келесі шарттар орындалуы тиіс: Сонымен осындай тәсілмен 5 Бравэ жазық
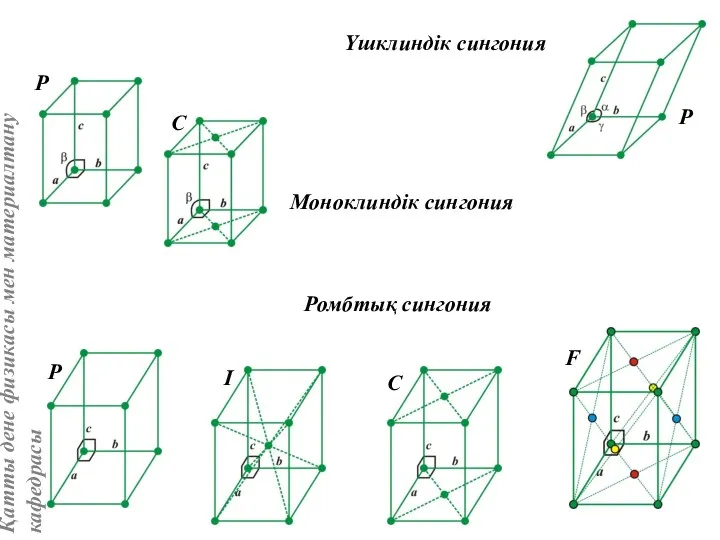
- 22. Моноклиндік сингония Ромбтық сингония Үшклиндік сингония
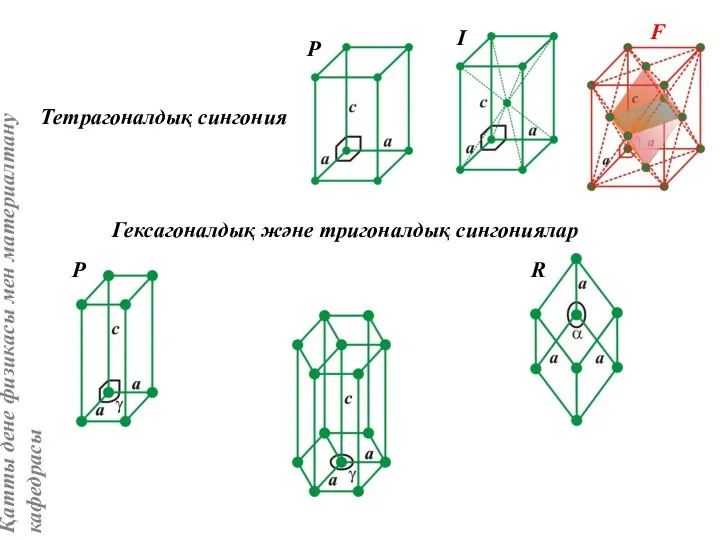
- 23. Тетрагоналдық сингония Гексагоналдық және тригоналдық сингониялар
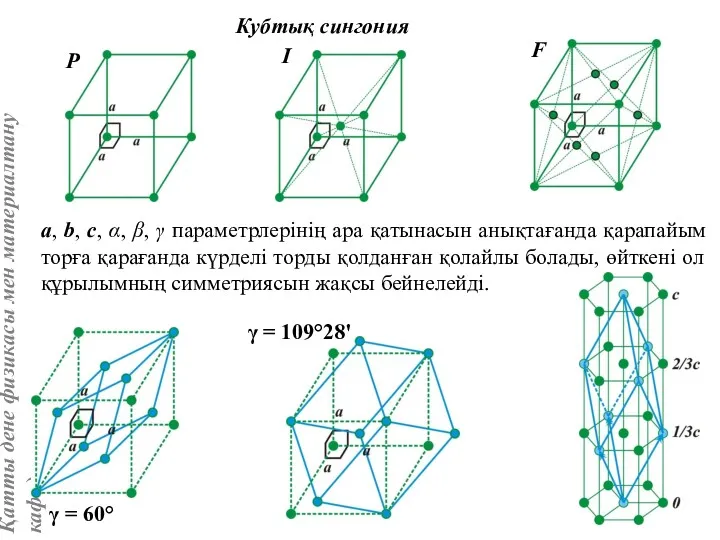
- 24. Кубтық сингония a, b, c, α, β, γ параметрлерінің ара қатынасын анықтағанда қарапайым торға қарағанда күрделі
- 25. Ұяшық көлеміне: Р-ұяшыққа – 1 түйін, I-ұяшыққа – 2 түйін, F-ұяшыққа – 4 түйін, С-ұяшыққа –
- 26. Базис – [[000]], негізгі трансляциялар a, b, c. Базис – [[000]], [[½½½]]. Негізгі трансляциялар a, b,
- 27. Кристалл құрылымында нүктелік симметрия тобына кіретін шекті симметрия түрлендірулеріне шексіз симметрия түрлендірулері қосылады. Кристалл құрылымының симметриясы
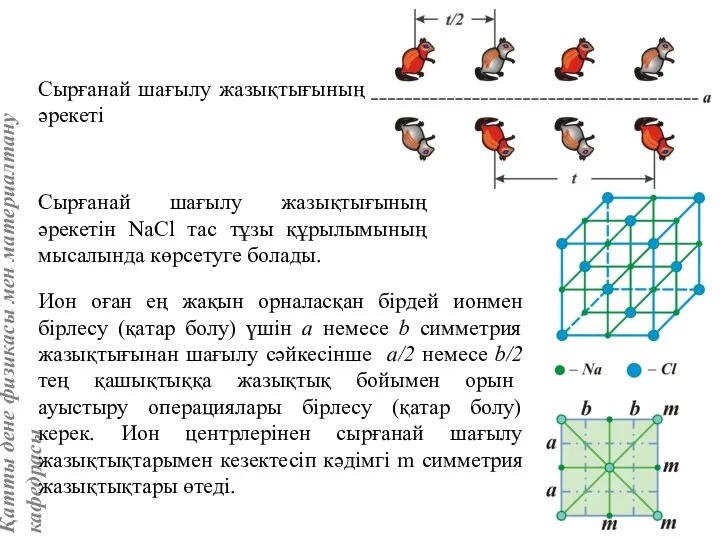
- 28. Сырғанай шағылу жазықтығының әрекеті Сырғанай шағылу жазықтығының әрекетін NaCl тас тұзы құрылымының мысалында көрсетуге болады. Ион
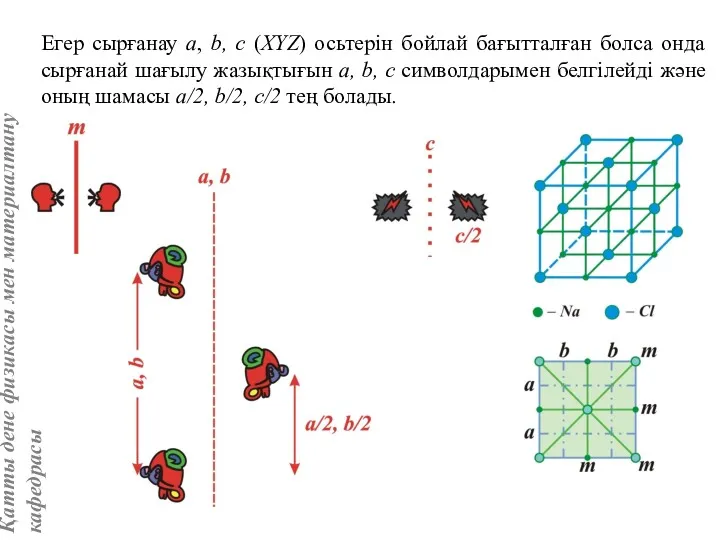
- 29. Егер сырғанау a, b, с (XYZ) осьтерін бойлай бағытталған болса онда сырғанай шағылу жазықтығын а, b,
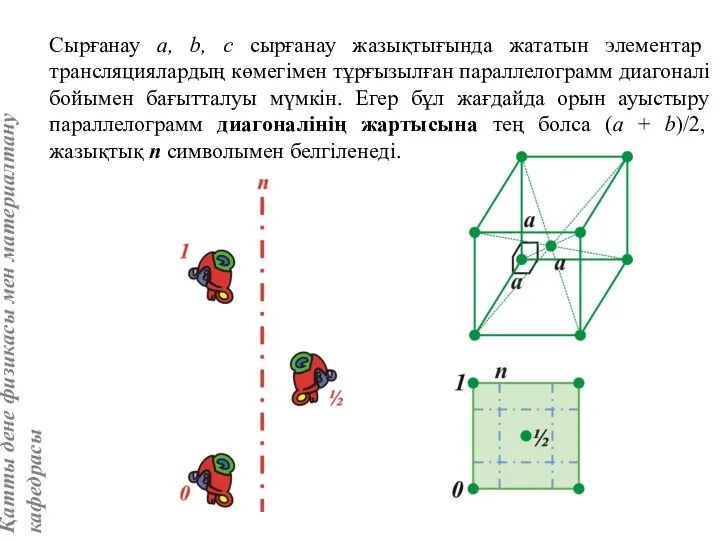
- 30. Сырғанау a, b, с сырғанау жазықтығында жататын элементар трансляциялардың көмегімен тұрғызылған параллелограмм диагоналі бойымен бағытталуы мүмкін.
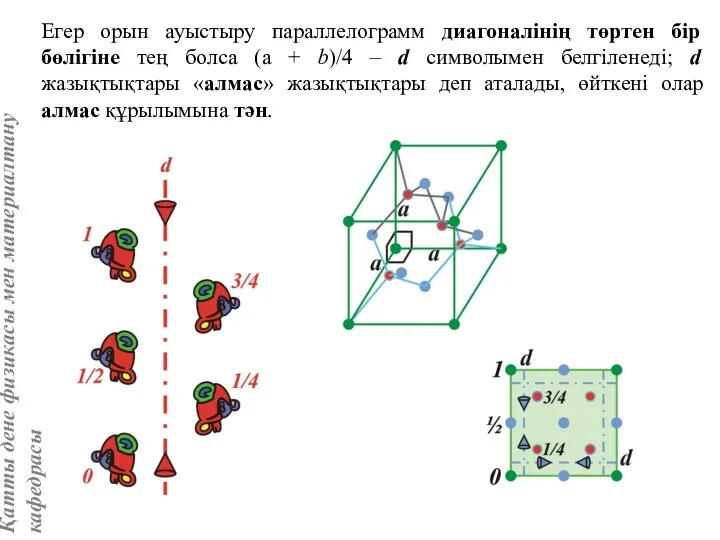
- 31. Егер орын ауыстыру параллелограмм диагоналінің төртен бір бөлігіне тең болса (а + b)/4 – d символымен
- 32. Трансляцияның симметрия осін айналу операциясына көбейтіндісі бұрандалық айналу операциясын тудырады. Симметрия осін айналу мен осы ось
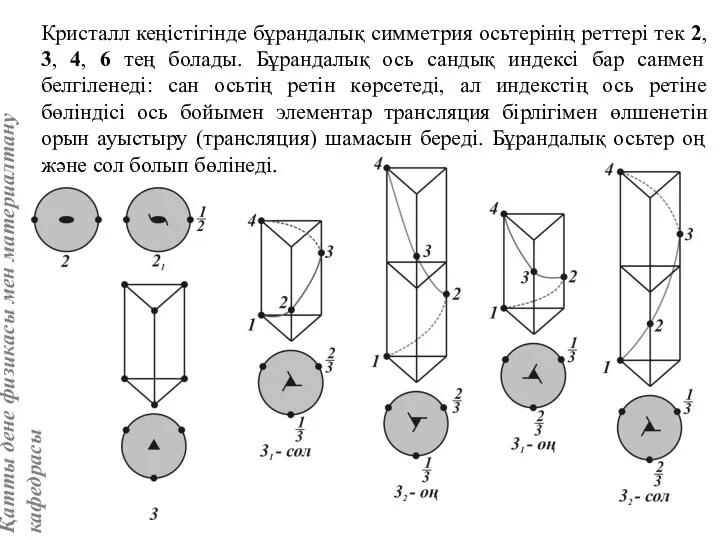
- 33. Кристалл кеңістігінде бұрандалық симметрия осьтерінің реттері тек 2, 3, 4, 6 тең болады. Бұрандалық ось сандық
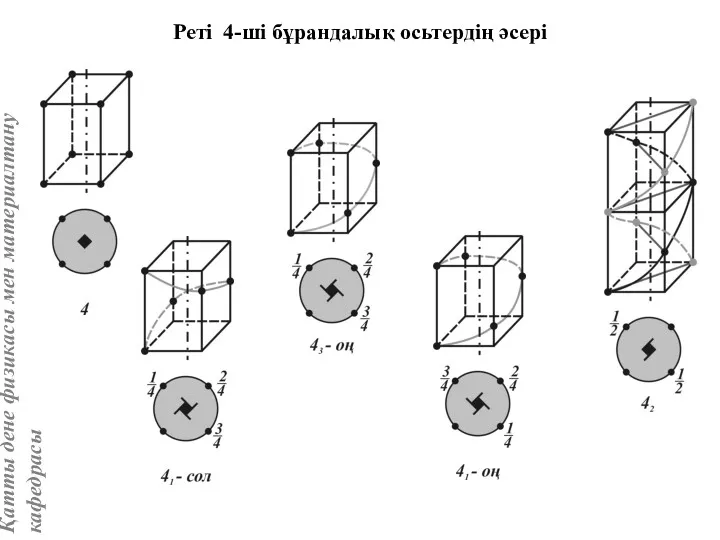
- 34. Реті 4-ші бұрандалық осьтердің әсері
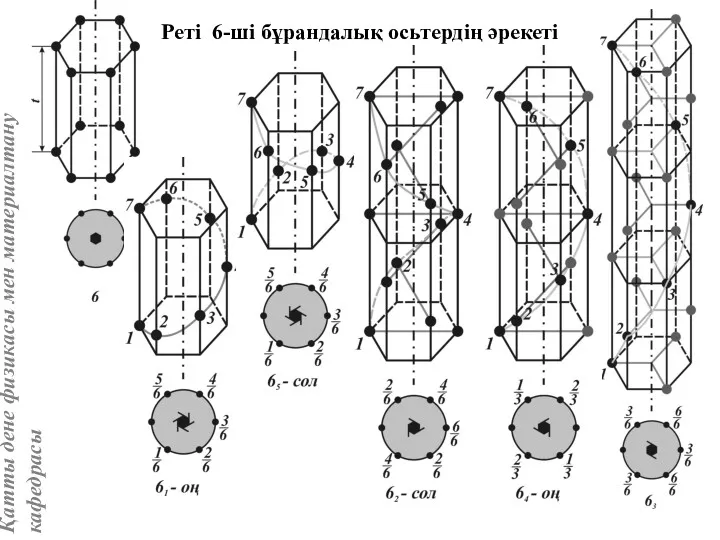
- 35. Реті 6-ші бұрандалық осьтердің әрекеті
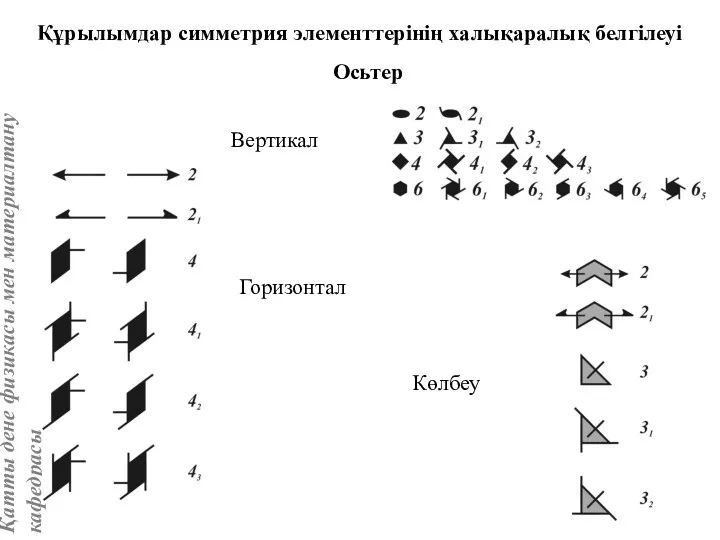
- 36. Осьтер Құрылымдар симметрия элементтерінің халықаралық белгілеуі Вертикал Горизонтал Көлбеу
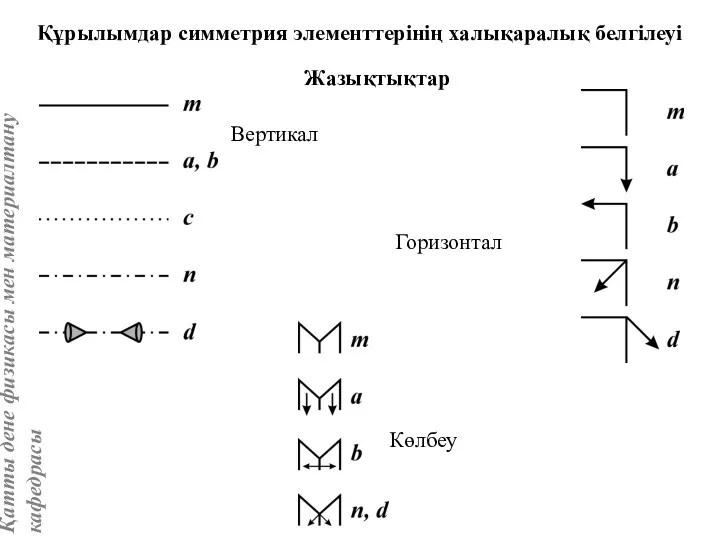
- 37. Жазықтықтар Вертикал Горизонтал Көлбеу Құрылымдар симметрия элементтерінің халықаралық белгілеуі
- 38. Құрылымның симметрия элементтерін көбейту көпқырлықтар симметриясын сипаттайтын 1-6 теоремаларына бағынады. Сонымен қатар шексіз қайталау қосылатындықтан жаңа
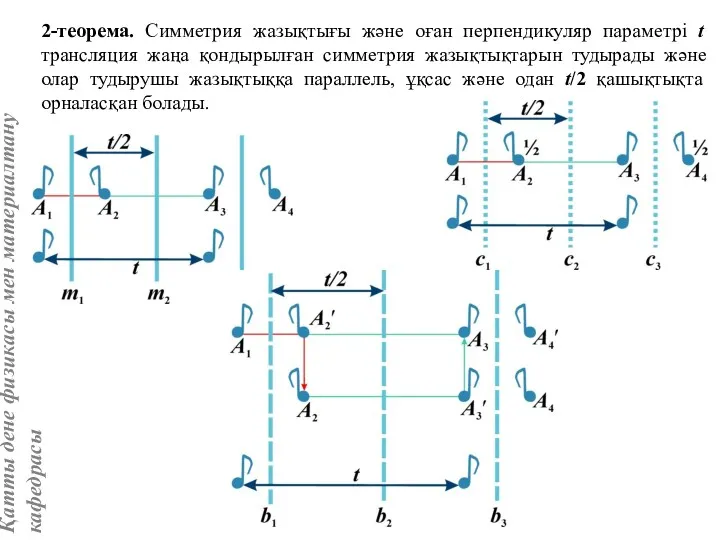
- 39. 2-теорема. Симметрия жазықтығы және оған перпендикуляр параметрі t трансляция жаңа қондырылған симметрия жазықтықтарын тудырады және олар
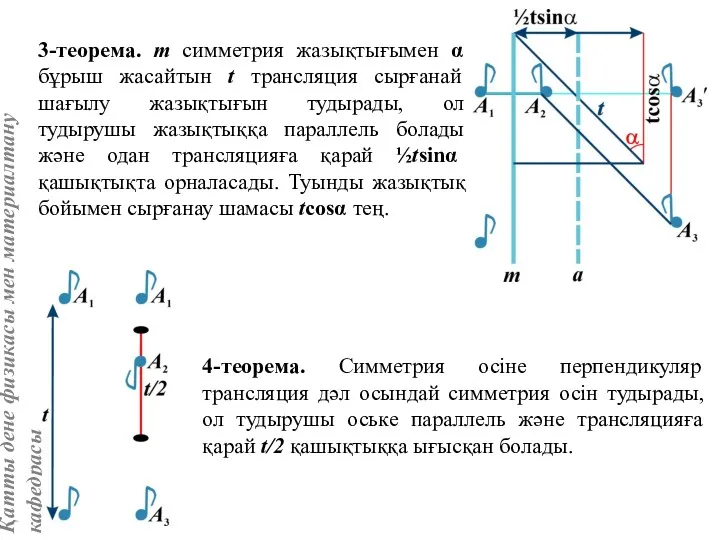
- 40. 3-теорема. m симметрия жазықтығымен α бұрыш жасайтын t трансляция сырғанай шағылу жазықтығын тудырады, ол тудырушы жазықтыққа
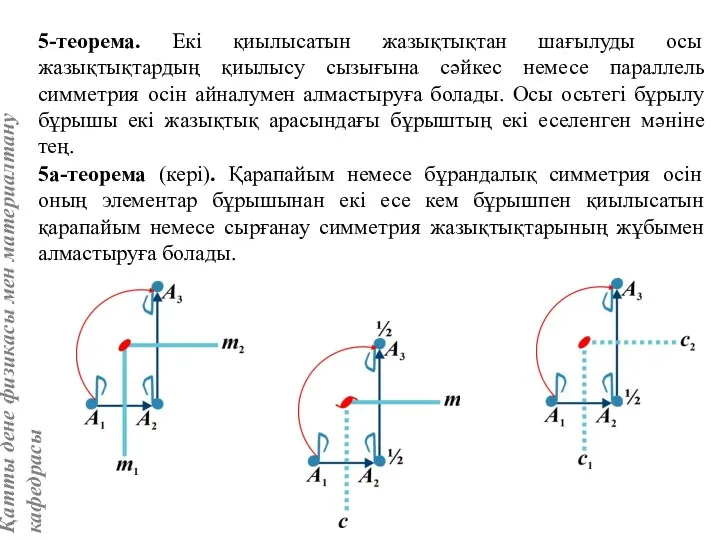
- 41. 5-теорема. Екі қиылысатын жазықтықтан шағылуды осы жазықтықтардың қиылысу сызығына сәйкес немесе параллель симметрия осін айналумен алмастыруға
- 42. Е.С. Федоров - құрылымдық кристаллографияның негізін қалаушы Ұлы орыс кристаллографы, минералогы, математигі Евграф Степанович Федоров 1853
- 43. Кристалл құрылымында барлық мүмкін болатын симметрия түрлендірулерінің терулері кеңістік симметрия тобы деп аталады. Нүктелік симметрия тобы
- 44. Кеңістік топтарын белгілеу үшін халықаралық символдары, сондай-ақ Шенфлис символдары және Е. С. Федоров символдары қолданылады. Нүктелік
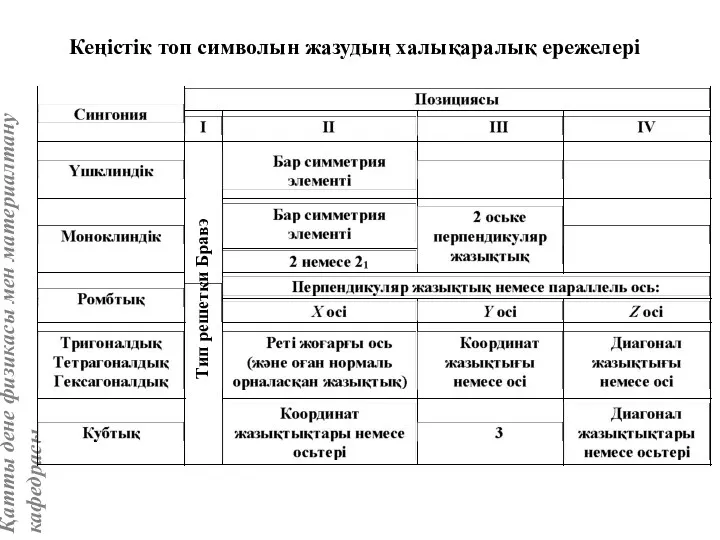
- 45. Кеңістік топ символын жазудың халықаралық ережелері
- 47. Скачать презентацию










![Базис – [[000]], негізгі трансляциялар a, b, c. Базис –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/10321/slide-25.jpg)






 Розв’язування задач з теми Закон збереження імпульсу
Розв’язування задач з теми Закон збереження імпульсу Subjects: forces in mechanics. Dynamics. Newton’s laws
Subjects: forces in mechanics. Dynamics. Newton’s laws Световые кванты
Световые кванты Резьбы, резьбовые изделия и соединения. Разъемные соединения. Неразъемные соединения
Резьбы, резьбовые изделия и соединения. Разъемные соединения. Неразъемные соединения Системы смазки и охлаждения двигателя
Системы смазки и охлаждения двигателя Гидростатика. Давление в жидкости
Гидростатика. Давление в жидкости DSI M78 6-Speed A/T. Overseas service team
DSI M78 6-Speed A/T. Overseas service team Геометрическая оптика
Геометрическая оптика Электромагнитное поле
Электромагнитное поле Отдельные электроприемники в однофазной цепи переменного тока
Отдельные электроприемники в однофазной цепи переменного тока Центрифугирование
Центрифугирование Өз құрылымы мен құрамы болмайтын бөлшекті
Өз құрылымы мен құрамы болмайтын бөлшекті Движение заряженной частицы в электрическом и магнитном полях. Лекция 6
Движение заряженной частицы в электрическом и магнитном полях. Лекция 6 Правило буравчика, правило правой руки
Правило буравчика, правило правой руки Кузнечно-сварочная практика. Специальность 190604 Техническое обслуживание и ремонт автомобильного транспорта
Кузнечно-сварочная практика. Специальность 190604 Техническое обслуживание и ремонт автомобильного транспорта Двигатель внутреннего сгорания. Устройство. Схема. Применение
Двигатель внутреннего сгорания. Устройство. Схема. Применение Движение тела под действием силы трения
Движение тела под действием силы трения Устройство токарного станка для обработки древесины. (Технический труд. 6 класс)
Устройство токарного станка для обработки древесины. (Технический труд. 6 класс) Вещества и явления в окружающем мире
Вещества и явления в окружающем мире Дизельный двигатель
Дизельный двигатель Физика в стихах
Физика в стихах Урок Оптические приборы, физика11 класс
Урок Оптические приборы, физика11 класс Отчет об исследовательской работе
Отчет об исследовательской работе Основы молекулярной физики и термодинамики
Основы молекулярной физики и термодинамики Идеальные газы тождественных частиц. Распределение Ферми-Дирака и Бозе-Эйнштейна
Идеальные газы тождественных частиц. Распределение Ферми-Дирака и Бозе-Эйнштейна Схема сверхзвукового обтекания затупленного тела
Схема сверхзвукового обтекания затупленного тела Оптические методы и приборы контроля качества продукции
Оптические методы и приборы контроля качества продукции Равновесные и неравновесные носители зарядов
Равновесные и неравновесные носители зарядов